非负弱下鞅的一类极大型φ-不等式

蔺 霞, 冯德成, 鲁雅莉

(西北师范大学 数学与统计学院, 兰州 730070)

1 引言与预备知识

目前, 关于弱鞅和弱下鞅[1]的研究已有很多结果. 例如: 文献[2]给出了弱鞅的极大值不等式及强大数定律; 文献[3]给出了弱下鞅的Whittle型不等式; 文献[4]给出了弱下鞅和N-弱上鞅的极大值不等式; 文献[5]给出了弱下鞅的极大值不等式以及非负弱鞅的极小值不等式; 文献[6]给出了非负下鞅的极大型φ-不等式.受文献[6]启发, 文献[7]建立了弱鞅的极大型φ-不等式; 文献[8]建立了条件弱鞅的极大型φ-不等式.本文利用Fubini定理以及Hölder不等式, 给出非负弱下鞅的一类极大型φ-不等式, 所得结果推广了文献[4]中的某些结论.

本文设{Xn,n≥1}或{Sn,n≥1}表示定义在概率空间(Ω,F,P)上的随机变量序列, 记X+=max{0,X},a∨b=max{a,b},I(A)表示集合A的示性函数, logx=logex=lnx, log+x=ln(x∨1).

定义1[1]设{Sn,n≥1}是L1(Ω,F,P)上的一列随机变量.如果对于j=1,2,…, 有

E[(Sj+1-Sj)f(S1,…,Sj)]≥0,

(1)

则称{Sn,n≥1}为弱鞅, 其中f为任意分量不减的函数并使得式(1)中期望有意义.如果进一步假设f是非负函数, 则称{Sn,n≥1}为弱下鞅.

设C表示Orlicz函数类, 即当φ∈C时,φ: [0,∞)→[0,∞)是一个无界不减的凸函数, 且φ(0)=0.令C′={φ∈C|φ′(x)/x在0点的某邻域内可积}.给定φ∈C且a≥0, 定义

令Φ(x)=Φ0(x),x>0.

2 主要结果

引理1[5]设{Sn,n≥1}是一个弱下鞅且S0=0, {cn,n≥1}是不减的正数序列, 则对任意的ε>0, 有

推论1设{Sn,n≥1}是一个非负弱下鞅且S0=0, {cn,n≥1}是不减的正数序列, 则对任意的ε>0, 有

证明: 由引理1及{Sn,n≥1}是一个非负弱下鞅, 易得结论.

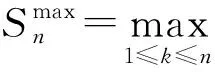
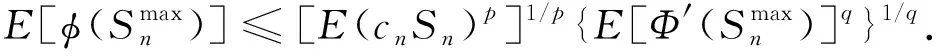
(2)

证明: 由推论1、 Fubini定理以及Hölder不等式, 可得

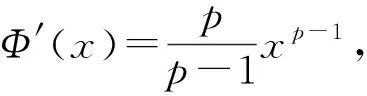
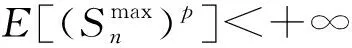
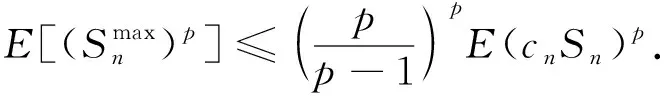
(3)

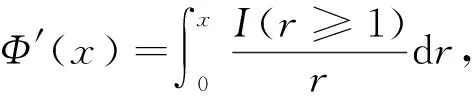
由于

alog+b≤alog+a+be-1,a≥0,b>0,

则

于是

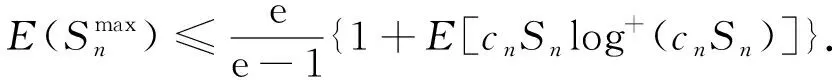
(4)

在式(4)中令ck=1,k≥1, 则

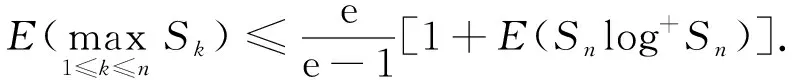
(5)

推论2设{Sn,n≥1}是一个非负弱下鞅且S0=0,φ∈C′, 则

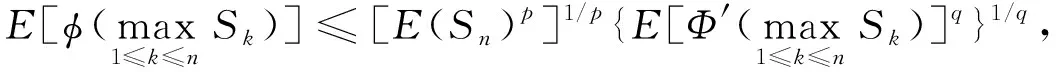
(6)

其中1/p+1/q=1,p>1.

证明: 在定理1中令ck=1,k≥1, 可得式(6).

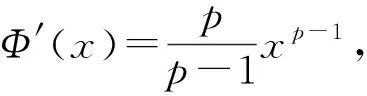
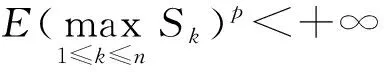
(7)

定理2设{Sn,n≥1}是一个非负弱下鞅且S0=0, {cn,n≥1}是不减的正数序列,φ∈C, 则对于任意的n≥1,t>0且0<λ<1, 有

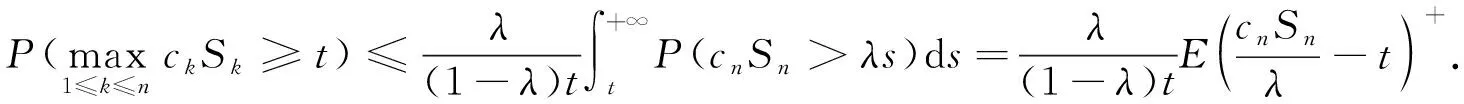
(8)

进而, 对于n≥1,a>0,b>0且0<λ<1, 有

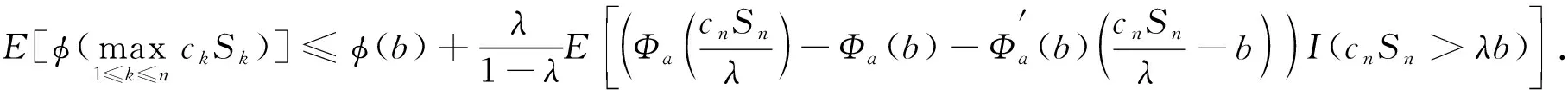
(9)

证明: 由推论1可得

于是

由于

故

从而

令b>0, 由式(8), 有

推论3设{Sn,n≥1}是一个非负弱下鞅且S0=0,φ∈C, 则

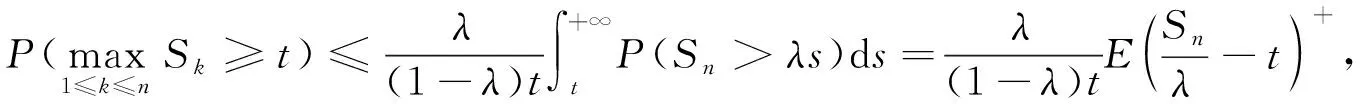
(10)

其中n≥1,t>0且0<λ<1.进而

(11)

其中n≥1,a>0,b>0且0<λ<1.

证明: 在定理2中令ck=1,k≥1, 可得结论.

注3推论3是文献[4]中定理3.1, 因此定理2推广了文献[4]中的结论.

定理3设{Sn,n≥1}是一个非负弱下鞅且S0=0, {cn,n≥1}是不减的正数序列,φ∈C, 则

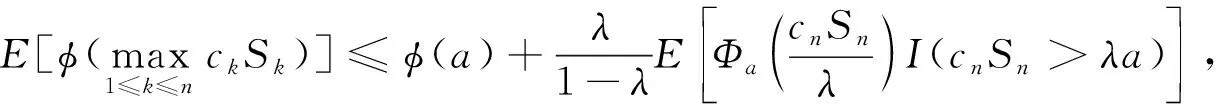
(12)

其中n≥1,a>0且0<λ<1.在式(12)中令λ=1/2, 则

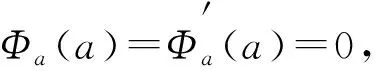
推论4设{Sn,n≥1}是一个非负弱下鞅且S0=0,φ∈C, 则

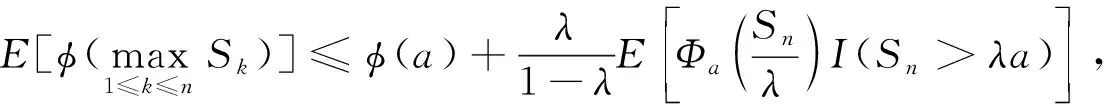
(13)

其中n≥1,a>0且0<λ<1.在式(13)中令λ=1/2, 则

其中n≥1,a>0.

证明: 在定理3中令ck=1,k≥1, 可得结论.

注4推论4在取I(Sn>λa)=1时, 即为文献[4]中定理3.2, 因此推论4推广了文献[4]的结论.

定理4设{Sn,n≥1}是一个非负弱下鞅且S0=0, {cn,n≥1}是不减的正数序列, 则

(14)

其中n≥1,b>1.

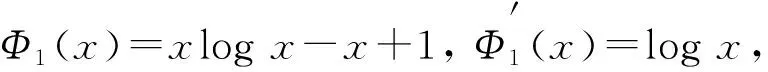
令b>1,λ=1/b, 则

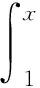
推论5设{Sn,n≥1}是一个非负弱下鞅且S0=0, {cn,n≥1}是不减的正数序列, 则

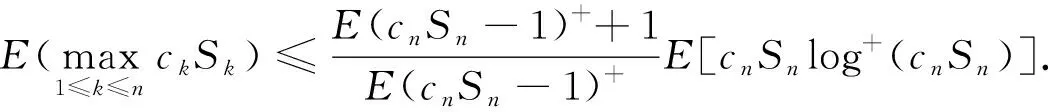
(15)

证明: 在定理4中令b=E[cnSn-1]++1, 可得式(15).

推论6设{Sn,n≥1}是一个非负弱下鞅且S0=0, {cn,n≥ 1}是不减的正数序列, 则

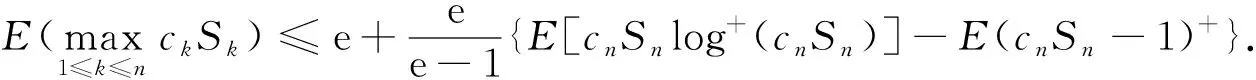
(16)

证明: 在定理4中令b=e, 可得式(16).

推论7设{Sn,n≥1}是一个非负弱下鞅且S0=0, 则

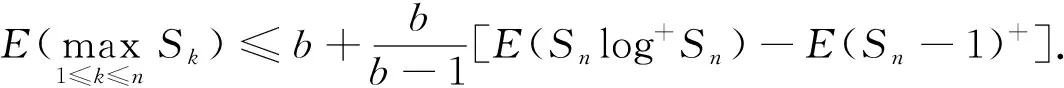
(17)

证明: 在定理4中令ck=1,k≥1, 可得式(17).