碳纤维平面三向机织物细观结构分析*

杨晓煜 焦亚男 杨晓亚

1. 天津工业大学纺织科学与工程学院，天津 300387；2. 天津工业大学先进纺织复合材料教育部重点实验室，天津 300387

三向机织物(Triaxial Woven Fabric，TWF)是由平面内三个不同方向的纱线或大丝束系统，以一定的角度(0°、60°和-60°)，按照特定交织规律彼此间相互交织而形成的一种平面三轴向织物[1]。因为TWF中的三组纱线系统相互间以60°的夹角进行交织，所以其面内存在规律性的正六边形空洞结构。这种空洞结构可以有效降低织物的面密度，对织物结构的轻量化具有重要的意义。

近年来，碳纤维平面三向机织物(Carbon Fiber Triaxial Woven Fabric，CFTWF)增强树脂基复合材料以其各向同性的力学性能和轻质的结构特点吸引了人们的极大关注[2-4]。当CFTWF制备的复合材料作为超薄材料使用时，其载荷分布更加均匀，深受航空航天行业的青睐，如卫星天线反射器[5]和可伸缩空间天线[6]等。此外，CFTWF还可以用作柔性复合材料的骨架材料，如人造革或橡胶基复合材料、橡胶基制动碗[7]等。

复合材料的力学性能很大程度上取决于复合材料内部纤维或纱线的取向和交织，因此需要深入地了解细观结构，准确理解细观结构的几何特征[8]。目前，国内外学者已对CFTWF的细观结构进行了研究。如：袁佳玲等[9]分析了相邻平行TWF纱线中心距和纱线宽度的关系，发现当纱线宽度与纱线中心距为1∶3 时，织物紧度为33.3%，织物结构的稳定性好。毕华阳等[10]通过几何解析法分析了碳纤维规格参数与CFTWF结构参数之间的关系。RAO等[11]将CFTWF中纱线的横截面形状设定为眼形椭圆形，并构建单胞模型，分析了织物结构中各参数之间的解析关系。但是该模型中，经纬纱的切点恰好处于单胞的中心线上，故建立的单胞模型是特定状态下的CFTWF横截面结构，不具备普适性。

目前，对于TWF细观结构的研究，大多是建立在三组纱线系统交织点处为紧密接触的理想条件下进行的，但实际服役用的织物结构中会存在一些间隙。因此，基于实际服役用织物的细观结构建立结构参数几何关系式，对CFTWF及其复合材料具有重要的意义。

本文将采用计算机断层扫描(Micro-CT)技术观察CFTWF增强树脂基复合材料的表面形貌和纱线截面细观形态，构建CFTWF单胞模型；随后基于建立的单胞模型，通过几何解析法，推导织物基本结构参数之间的关系式，讨论三组纱线系统因存在交织间隙而形成的三角形空洞对CFTWF结构参数的影响。

1 CFTWF细观结构及其单胞模型的构建

1.1 CFTWF细观结构

在CFTWF细观结构中，三组纱线系统中的任意两组纱线系统都是以60°的夹角相互交织在一起的。当每组纱线系统内相邻纱线间距大于纱线宽度时，CFTWF面内呈现出规则分布的正六边形空洞结构。但实际织造过程中，由于碳纤维无捻丝束的特性和编织工艺条件的限制，三组纱线系统的交织处不能形成紧密接触，会出现很小的三角形空洞。因此，CFTWF在实际服役时，其细观结构呈正六边形空洞和较小正三角形空洞相间的规则分布，具体如图1所示，其中θ为编织角，理论值为60°。

图1 CFTWF 实物照片

1.2 CFTWF细观结构单胞模型的构建

1.2.1 CFTWF单胞模型假设

为了研究CFTWF中纱线的屈曲形貌，采用Micro-CT扫描技术对其进行表征。图2a)为CFTWF表面细观形貌扫描图像，其中：L为纱线中心距，即相邻两根平行纱线之间的垂直距离；c为纱线宽度；a1表示六边形空洞的边长；a2表示三角形空洞的边长。沿图1中的KK1虚线垂直分割CFTWF实物，可得到CFTWF横截面扫描图像[图2b)]，其中：L′为相邻两根纱线之间的距离即纱线间距，L=2L′；a和b分别为纱线斜截面的高度和宽度。同理,沿图1中的NN1虚线垂直分割CFTWF实物，可得到CFTWF纵截面扫描图像[图2c)]。

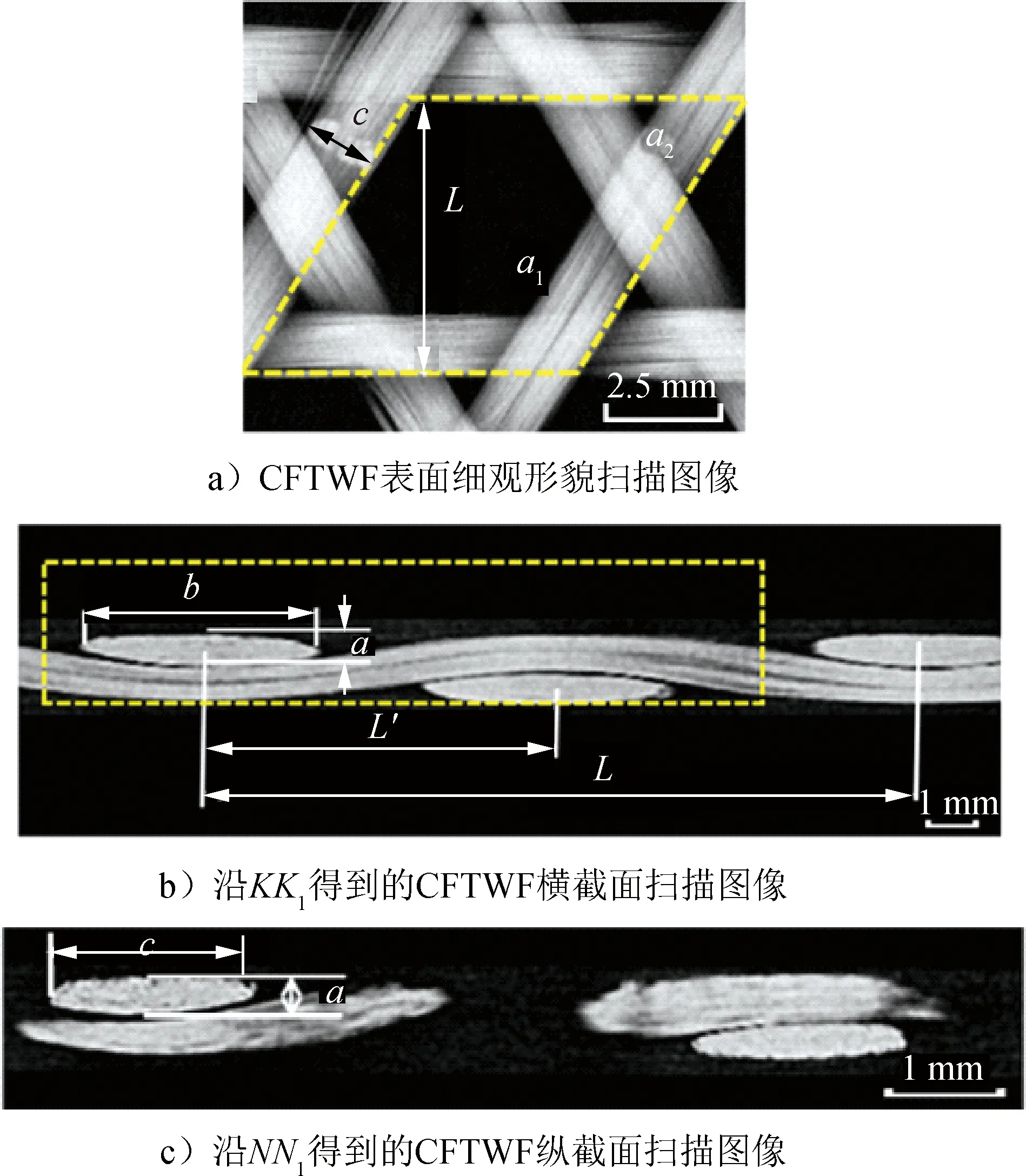
图2 CFTWF扫描图像

由于纱线是以60°的夹角相互交织在一起的，故0°纱线与NN1截面呈90°夹角，60°纱线和-60°纱线与KK1截面呈60°夹角。因此，图2b)和c)中，0°纱线与-60°纱线的截面形状不相同。图2b)中，60°纱线呈现的是纱线的斜截面；图2c)中，0°纱线呈现的是纱线的横截面。

图2显示了CFTWF的几何特征，其中纱线的中心距、纱线屈曲的形状轨迹和纱线的截面形状是最主要的三个特征。本文为便于分析，对CFTWF的关键结构做出了如下假设：

(1)在纱线长度方向上，纱线周期性的屈曲形状被假设成一条直线段加两条圆弧线段；

(2)纱线斜截面形状类似凸透镜，并在纱线轨迹方向上保持不变；

(3)单根纱线是一个连续体，其体积密度保持不变；

(4)三组纱线系统的线密度、体密度、纱线屈曲形状轨迹和截面形状皆相同。

1.2.2 CFTWF面内结构单胞的选取

基于对CFTWF中纱线交织规律的分析，选取如图2a)中平行四边形虚线框所示的部分作为CFTWF面内结构单胞。

1.2.3 CFTWF横截面细观结构单胞的选取

为研究CFTWF横截面的细观形貌，选取图2b)矩形虚线框所示部分作为CFTWF横截面细观结构单胞。

2 细观结构解析模型

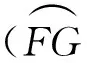
图3 CFTWF横截面细观结构单胞模型

2.1 CFTWF面内细观结构参数分析

利用几何解析的方法分析CFTWF横截面细观结构参数，推导三角形空洞边长a2、织物孔隙率ν和面密度w等基本结构参数的关系式。

2.1.1 三角形空洞边长a2

结合图2a)所示的CFTWF面内结构单胞，a2和L可分别表示为：

(1)

(2)

联立式(1)和式(2)，可得到纱线中心距L与三角形空洞边长a2、纱线宽度c的关系式：

(3)

三角形空洞边长a2在设计初始属于未知参数。假设a2=nc，n∈[0.00,∞)，则式(3)可转化为：

(4)

式(4)表征了纱线中心距L与纱线宽度c的关系。

2.1.2 织物孔隙率ν

在CFTWF面内结构单胞中，六边形空洞和三角形空洞面积之和与CFTWF面内结构单胞总面积的比值即为CFTWF孔隙率，用ν表示。

六边形空洞面积SH：

(5)

三角形空洞面积ST：

(6)

CFTWF面内结构单胞总面积Scell：

(7)

那么，CFTWF孔隙率ν：

(8)

再结合式(1)及假设a2=nc，n∈[0.00,∞)，可得到CFTWF孔隙率ν与系数n的关系式：

(9)

2.1.3 CFTWF面密度w

CFTWF面密度为纱线质量与CFTWF面内结构单胞总面积之比：

(10)

式(10)中：w为CFTWF面密度，g/m2；m为纱线质量，g；Scell为CFTWF面内结构单胞总面积，m2；Nt为纱线线密度，tex；L为纱线中心距，mm。

2.2 CFTWF截面结构参数分析

CFTWF截面结构参数分析步骤：(1)构建单胞模型；(2)利用几何解析方法分析纱线横截面和纱线斜截面的关系；(3)利用参数表征纱线截面形状的变化；(4)推导纱线厚度T的几何关系式。

2.2.1 纱线横截面

根据图3的单胞模型，可以建立纱线横截面和纱线斜截面的参数关系式：

a=2r(1-cosβ)

(11)

b=2rsinβ

(12)

c=bsinθ=rsinβsinθ

(13)

联立式(11)和式(12)可以得到组成纱线斜截面圆弧的半径r和角度β：

(14)

(15)

纱线横截面面积S2与纱线斜截面面积S1的关系：

S2=S1sinθ

(16)

其中，纱线横截面面积S2：

(17)

式(17)中：ρ为碳纤维的体密度；∂为碳纤维的填充因子，一般取0.7。

联立式(16)和式(17)可建立纱线斜截面面积S1与碳纤维纱线线密度Nt的关系式：

(18)

2.2.2 纱线斜截面

不同纱线中心距L的CFTWF横截面中，相同线密度的碳纤维纱的斜截面形状是不同的(图4)。本文利用长短径比系数(aspect ratio，kAR)和圆度系数(Circularity，kCirc)表征截面的变化:

(19)

(20)

图4 T300-6K碳纤维纱线在不同纱线中心距L的 CFTWF中的横截面照片

由式(19)和式(20)可知，长短半径比系数kAR和圆度系数kCirc只和圆弧角度β有关。如图5所示，黄色部分为不同圆弧角度β(30°、40°、50°、60°)对应的碳纤维纱线的截面形状，可以看出，随着圆弧角度β的增加，长短半径比系数kAR逐渐减小，圆度系数kCirc逐渐增加，纱线扁平程度越来越低。

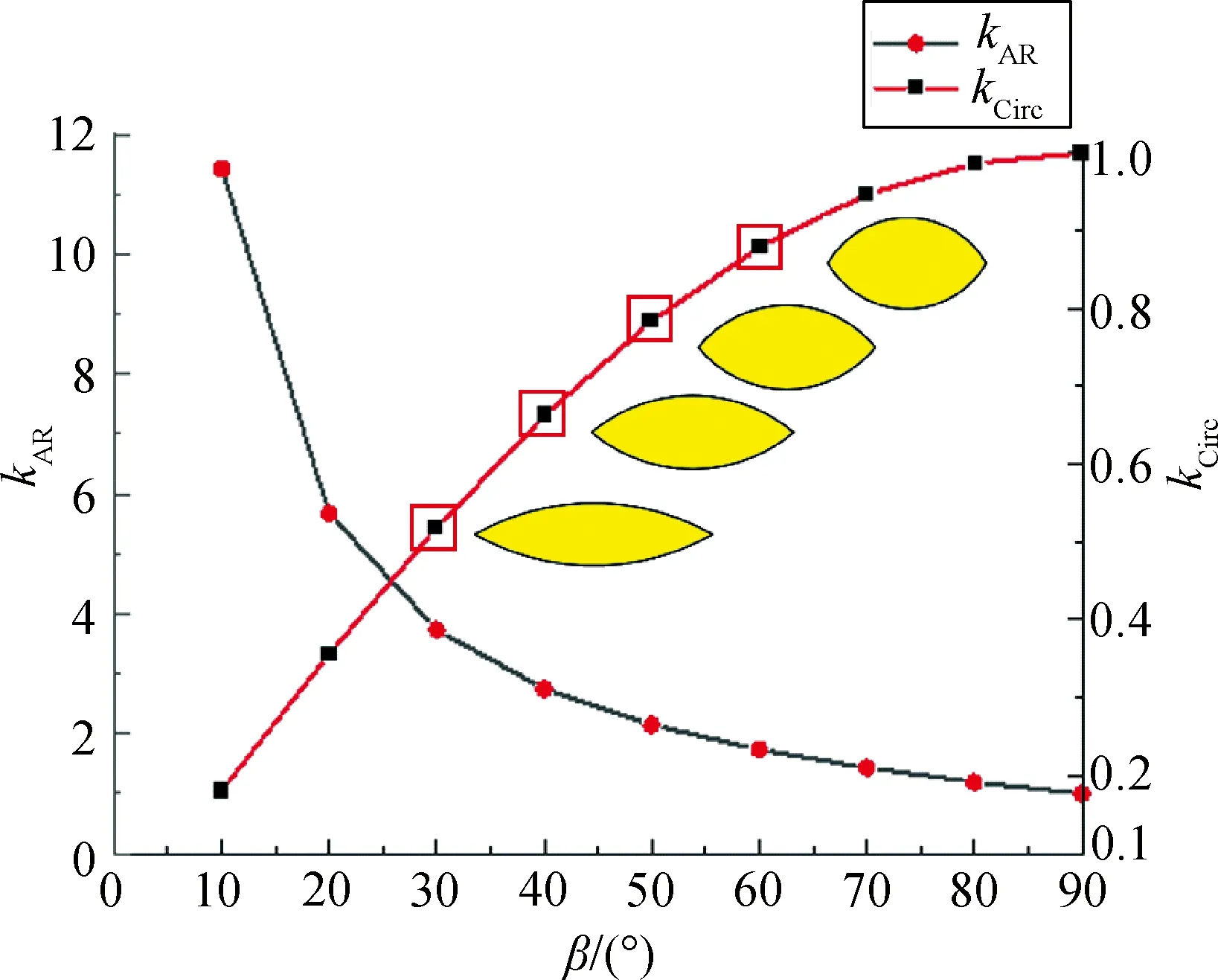
图5 圆弧角度β与长短半径比系数kAR、 圆度系数kCirc的关系

2.2.3 织物厚度T与纱线屈曲角α

根据图3的CFTWF横截面细观结构单胞模型可以得到：

(21)

(22)

(23)

(24)

(25)

(26)

再结合式(11)可得织物厚度T：

T=hw+a=[L′-2r(2-cosβ)sinα]tanα+

2r(2-cosβ)(1-cosα)+2r(1-cosβ)

(27)

由式(27)可知，厚度T与纱线间距L′、纱线截面圆弧半径r、圆弧角度β及纱线屈曲角α有关。

2.3 模型验证

表1列出了CFTWF中三角形空洞边长a2、织物面密度w、织物厚度T的计算值与测量值。从表1可以看出，计算值与实际值的相对误差最大为8.29%，表明细观结构单胞模型具有较高的准确性。因此，在实际工程中，可通过测量纱线斜截面高度a、纱线斜截面宽度b、纱线中心距L和屈曲角α，解析CFTWF细观结构单胞模型中的三角形空洞边长a2、织物面密度w、织物厚度T等结构参数，然后利用这些结构参数之间的关系，优化CFTWF编织工艺，预测CFTWF的细观形貌。

表1 CFTWF中结构参数的计算值与实测值

3 三角形空洞对织物细观结构参数的影响

三角形空洞的存在对CFTWF孔隙率ν有一定的影响。

图6反映了3种系数n的CFTWF面内结构，其中n=0.00和n→∞是两种极限状态，而现实是处于两种极限状态之间的。

图6 系数n 与CFTWF的结构关系

下面将从三角形空洞系数n入手，分析三角形空洞边长a2对L/c(纱线中心距L与纱线宽度c的比值)和织物孔隙率ν的影响。

图7反映了CFTWF中L/c与n的关系。图7中，n的取值范围为[0.00,1.50]，递进量为0.05，L/c从3.000逐渐增加到5.598。当n为0.00时，L/c为3.000，三角形空洞边长a2为0.000 mm，即此时三角形空洞完全被填充消除[图6a)]。随着n的增加，L/c增加，CFTWF中出现三角形空洞。

图7 CFTWF中系数n与L/c的关系

CFTWF中系数n与织物孔隙率ν的关系如图8所示。图8中，n的取值范围为[0.00,1.50]，递进量为0.05，孔隙率ν从0.33逐渐增加到0.56。

图8 CFTWF中系数n与织物孔隙率v的关系

4 结论

通过对CFTWF中纱线屈曲形态与交织规律进行分析，采用几何解析方法，推导出CFTWF细观结构参数，准确描述了纱线几何构型特征，同时考虑了三角形空洞存在的实际情况，得出：

(1)CFTWF在实际服役时，其结构是以正六边形空洞和正三角形空洞相间规则分布的。

(2)三角形空洞是CFTWF细观结构分析中的一项影响因素。当系数n为0.00时，三角形空洞消除，织物孔隙率ν为0.33。随着系数n的增加，三角形空洞面积增加，织物孔隙率ν增加。

(3)细观结构单胞模型和计算式的建立为CFTWF复合材料参数的设计提供了理论和实际参考。