基于PCA-XGBoost联合算法的盗窃犯罪预测模型

朱小波 栗赫遥

(上海公安学院治安系 上海 200137)

0 引 言

犯罪活动具有复杂性和多样性的特点，直接影响着社会安定和人民安全。目前，大量研究成果表明犯罪活动虽复杂多变，但基于犯罪行为发生的条件限制，必然与犯罪时间、犯罪空间、犯罪人等因素产生特定关系，通过对相关因素进行分析，不但可以总结犯罪规律，而且可以通过建立数据模型预测犯罪发生，达到主动响应、提早预防的效果。现如今，随着海量犯罪数据的“历史积淀”，对其进行深度挖掘和推理，已然成为公安机关在大数据时代的必然选择。作为最常见的侵犯财产类犯罪形式之一，盗窃犯罪不仅案发量高而且极易演变至其他类型的犯罪，社会危害性较大，人民群众对此深恶痛绝。因此，对盗窃犯罪特征因素分析以及预测模型的建模研究，不仅有助于发掘该类犯罪的特征向量，尽早采取措施进行有效预防，同时对间接降低其他类型案件的犯罪率，提升社会面整体治安水平都有所裨益。

早在19世纪30年代，美国纽约市警察局就采用数据分析方法预测犯罪问题。警察局的分析人员通过将犯罪的地理空间等信息用图钉分别标注于地图上，运用归纳分析、关联分析和逻辑推理的方法找出犯罪发生的规律，并结合多年从业经验，最终进行犯罪数量和易发案区域进行预测。时至今日，随着信息技术和人工智能的不断发展和应用，越来越多的学者通过地理信息系统、机器学习与数据挖掘等技术方法的结合，对犯罪数据进行综合分析与预测。基于大数据的犯罪预测不仅能够摆脱个人经验的偏见影响，还有助于优化警力配置，实现多维度预防犯罪。例如，决策树算法就可以多条件向下划分针对复杂分类问题给出有预见性的分类结果，从而达到预测犯罪趋势的效果[1]。金光等[2]运用决策树算法构建预测模型，探索出了适用于犯罪预测领域的数据挖掘方法。李卫红等[3]通过对某市犯罪历史数据的学习及训练建立改进后的GA-BP神经网络模型。国外也有学者将研究区域划分成一个个单元格，通过logistic回归和神经网络两种犯罪预测模型相互结合的方式对研究地理区域的单元格进行犯罪预测[4]。还有学者从原始犯罪数据当中提取数据集，通过数据挖掘构建不同分类器模型，从而达到犯罪预测的目的[5-7]。

犯罪数据往往具有样本信息复杂多变、样本量大等特点，对其进行精确预测具有一定的难度。本文为实现此目的，将引入主成分分析(PCA)法和XGBoost法，即：将多变量数据降维与极端梯度提升分类算法相结合，使用迭代运算方法将大量的弱分类器组合成强分类器，能够有效地构建增强树并实现并行运行。

1 数据概述

由于国内犯罪数据的涉密性，本文选取2017年美国芝加哥市的盗窃犯罪的911报警数据集，依次进行数据概况描述、数据筛选和数据清洗等预处理工作。最终在原始样本中获取了分组聚合成48 126个有效数据，数据集字段包括案件ID、犯罪日期分段标注、所属街区、案件描述、所属分局、所属社区、犯罪所在经纬、维度和聚合计数后的案件发生次数等。数据集主要字段信息如表1所示。

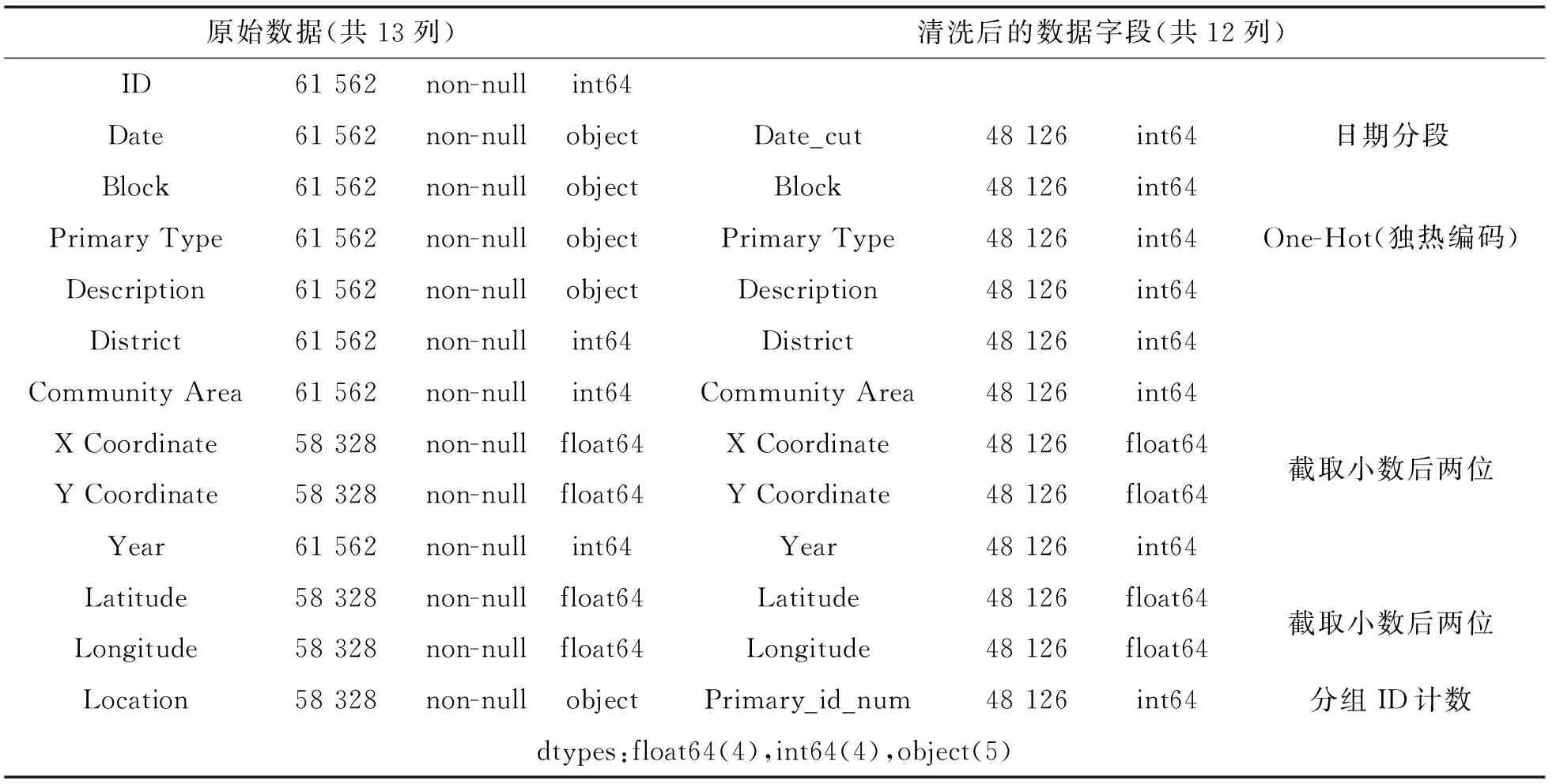
表1 数据集字段表

2 基于PCA-XGBoost算法的盗窃犯罪数量预测模型

基于PCA-XGBoost算法的盗窃犯罪数量预测模型可以概括为以下几个步骤：首先，利用盗窃犯罪报警数据集的PCA处理，形成犯罪数量的特征矩阵；然后，构建犯罪数量预测模型，包括预测模型优化和定模；最后，基于统计数据进行犯罪数量预测。如图1所示。

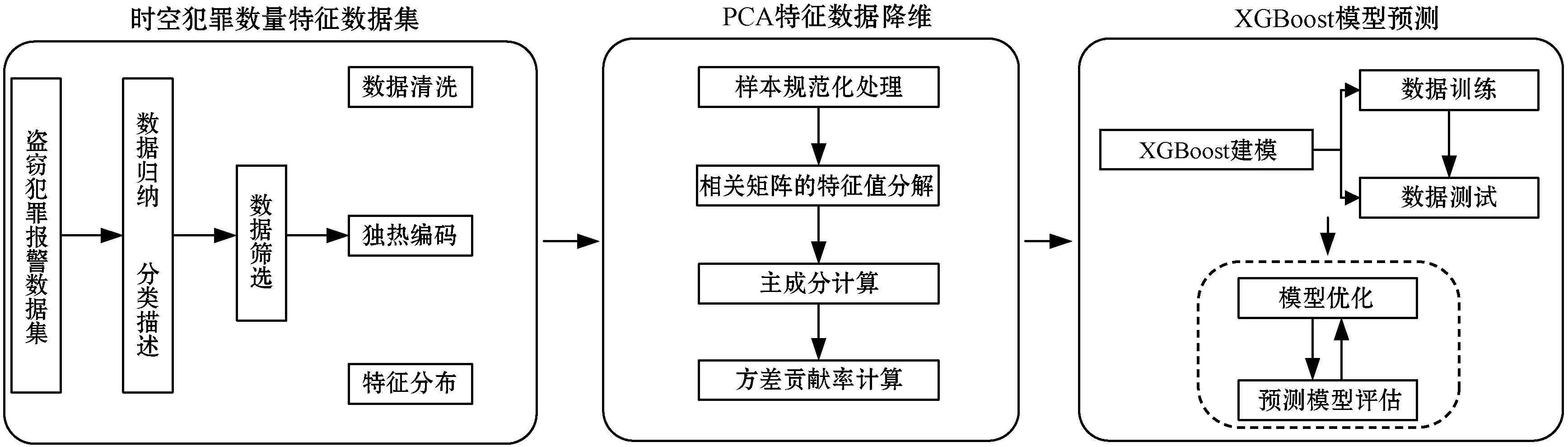
图1 基于PCA-XGBoost算法的盗窃犯罪数量预测模型框架

2.1 主成分分析方法

PCA是一种无监督学习、多元统计分析方法，用于发现数据基本结构，实现多变量数据降维，其主要实现步骤如下：

(1) 样本数据规范化处理。

(1)

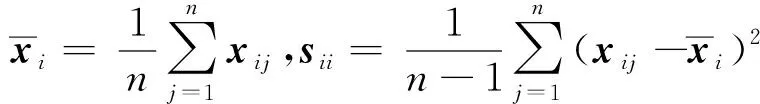
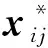
(2) 样本协方差矩阵的特征值分解。

求解s的特征值方程：

|s-λI|=0

(2)

得到s的m个特征值λ1≥λ2≥…≥λm，与之相对应的特征向量为(ξ1,ξ2,…,ξm)。

(3) 主成分计算。

(3)

(4) 计算主成分的方差贡献率。

(4)

式中：ρi表示第i个主成分的方差贡献率。

2.2 XGBoost算法和基本原理

XGBoost(eXtreme Gradient Boosting)是基于梯度提升迭代决策树算法优化而来的极端梯度增强分类算法，具有高效、并行、精确和鲁棒性好等优点。在同样条件下，XGBoost算法的运算能力、训练速度以及预测速度比其他算法更著优势。由于XGboost具有自动分裂学习能力，其目标函数考虑了二阶导数的影响，使损失更精确，极大提高了算法的效率。因此，XGBoost非常适合应用于在时间不连续、空间间隔性下的盗窃犯罪数量预测。

XGBoost目标函数和优化推导如下：

1) XGBoost考虑正则化项，目标函数定义如下：

(5)

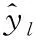
依据上述模型框架，可以优化出树的建模函数ft(x)：

(6)

2) 每次建树优化以下目标：

(7)

3) 假设已知树结构q，即每个样本xi能通过该结构q找到相对应的树叶子节点j，可以定义Ij={i|q(xi)=j}为在树结构q下，落入叶子节点j所有样本序号的集合。对上述表达式进行展开并通过配方法，就可以得到：

(8)

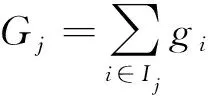
最终得到叶子权重值为：

(9)

4) 最终的目标值为：

(10)

3 盗窃犯罪数量预测模型构建

本文利用经过清洗后的2017年芝加哥的盗窃犯罪的911报警数据集的80%作为模型的训练集，将剩余的20%作为测试数据集用来验证模型精度。

3.1 建模思想

数据中考虑到大量日期上的分散性，对日期数据进行步长处理，每月按照上中下三类作区分，对日期步长、街区、区域和经纬度等，按犯罪发生次数分组聚集计数。因案件类型、街区和案件描述字段是属性变量，需要进一步进行类别数值划分，本文采用独热编码(One-Hot))，把属性变量转化为数值型变量，可以认为和统计学中单位标准向量相同，向量元素只有0和1，即N种属性类型变量对应N种状态列，如有两个属性变量，其中两个变量去重值数量对应为n×m(N)，由独热编码方式映射的向量矩阵就是m×n型的不严格的标准单位矩阵，如此把属性类变量归一到二进制向量上，将出现状态对应的视为整数索引标记为1，其他的空缺情况标记为0。此编码方式可将离散的序列扩展到欧氏空间，编码之后，一方面在计算和刻画特征之间的距离和离散化程度刻画上更加便捷，另一方面也方便对特征向量进一步实现特征工程和模型构建，达到预测的目的。

本文数据列中的两列犯罪描述和犯罪类型可以形成3×2的向量矩阵，可以表示为“RETAIL THEFT”=>[1，0，0，0，0，0]，“ATTEMPT THEFT”=>[0，1，0，0，0，0],“OVER ＄500”=>[0，0，1，0，0，0]等。

3.2 特征向量构建

结合先验经验与数据可得性，本文从时间、空间经纬度、所属街区等方面分裂出15个维度指标作为模型特征向量，然后采用PCA方法提取特征成分，具体各特征的重要性程度如图2所示。

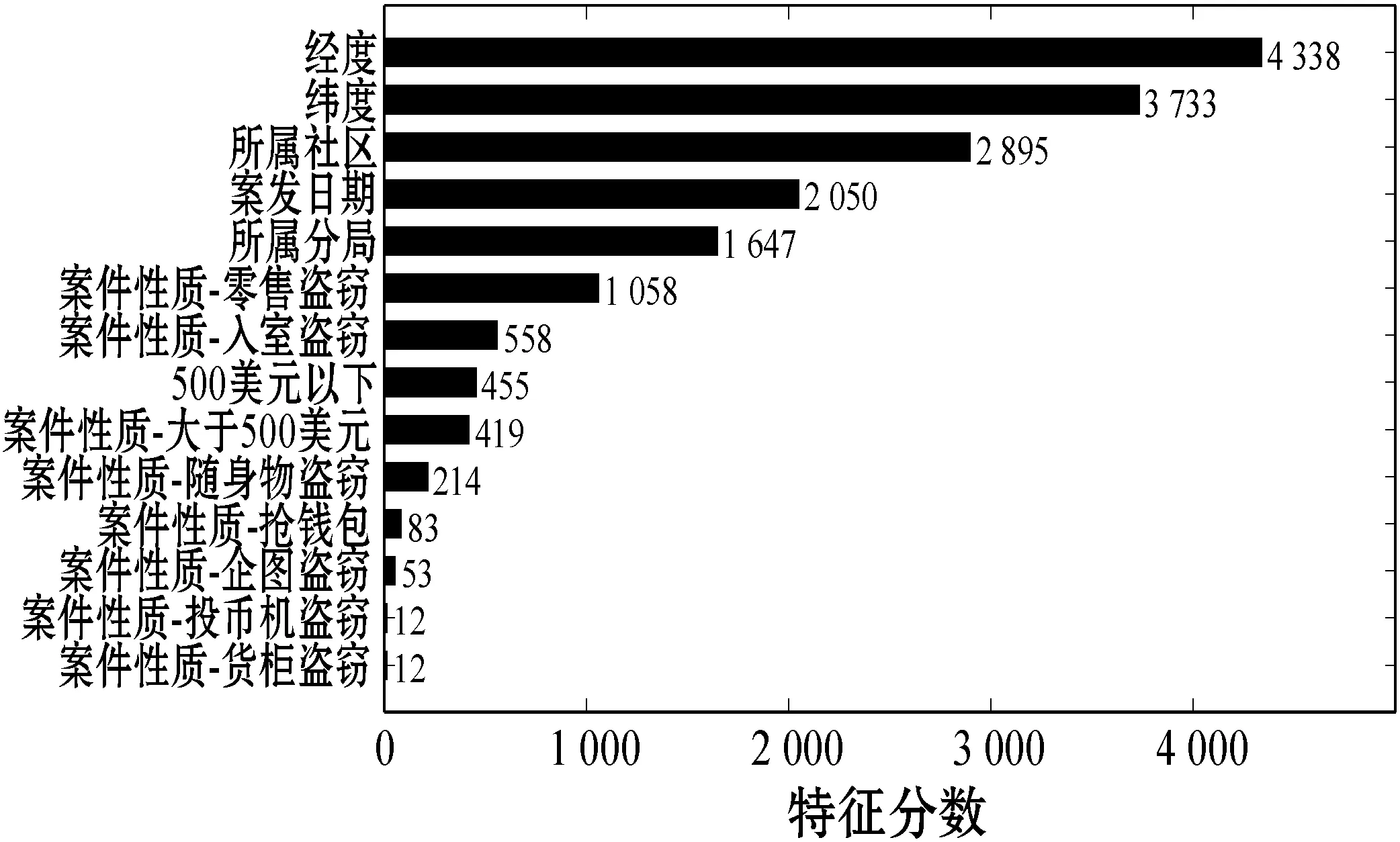
图2 特征重要性图

3.3 模型评估

在所选择的训练集下训练出的模型仍需进一步验证模型的精确性和准确性。

本文选择了三种方法：

(1) 从测试集和预测数据集真实数值出发，计算预测集和实际测试集的差值，选择均方根误差(RMSE)作为第一个模型评估的方法。

(2) 采用分类正确率(AUC)，即：ROC曲线覆盖面积大小，该指标考虑了正例和负例排序得分问题。

对于XGboost.train参数进行调优：

& early_stopping_rounds=10

& eval_metric=′mlogloss′

& eval_set=eval_set

& verbose=True

& learn_rate=0.01

& early_stopping_rounds：早期停止次数，本模型设为10。

& evals：用于对训练过程中进行评估列表中的元素列表。形式是evals=[(dtrain,′train′),(dval,′val′)]或者是evals=[(dtrain,′train′)],用于训练过程中观察验证集的效果。

& learning_rates：每一次提升的学习率的列表。

& eval_metric：选择的损失函数类型。

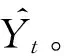
均方根误差的公式如下：

(11)

式中：n代表犯罪指标的样本数。

犯罪数量预测误差分布直方图情况来看，如图3所示，在各测试值加上均方误差值(1.60)变化情况，85.6%以上的犯罪数量误差率在30%以内，平均准确率达到80.6%。

图3 犯罪数量预测误差分布直方图

本文采用的另一种衡量指标AUC作为本次犯罪预测模型的精准度判定。AUC即为ROC曲线下的面积大小，AUC一般对应于二分类逻辑回归中衡量分类模型的精准度，表示得到的正例预测排在负例前面的概率，可以理解为在本文选择的正、负两个样本中分别赋予的得分的对比情况，每一个分类器对应给出正样本得分高于负样本的概率大小。具体方法为：首先对样本得分进行降序排列，得分最高的样本对应为n，依次向下排列，最终得到的是n-1,…,1序列形式，可以算出正例样本的数量(减去两个正例样本交叉重复出现的情况)和正样本得分大于负样本得分数值，与总数的比值即为所求，即：

(12)

最后采用的另外一种评价方法：F1分数。与AUC模型相同，F1分数同时考虑了准确率以及召回率的影响。但是从模型优化角度来看，AUC的优化目标是训练一个偏保守的不误报的模型，而F1分数的优化目标是训练一个偏激进的不放过任何可能的模型。综合两者考虑，能够综合两者各自的优点。F1分数的计算公式如下所示：

(13)

式中:P代表Precision，即准确率；R代表Recall，即召回率。

4 模型的对比验证

4.1 K折交叉验证法迭代(K-CV)

考虑到在实验中选出的训练集训练出来的模型在实际使用测试和模型预测中可能出现参数拟合欠佳和过拟合，为了提高模型的泛化能力和其对应的最优超参值，本文选择利用K折交叉验证方法对参数进行迭代调优，找到一个更具说服力的最优超参值，并运用到训练集上重新训练模型，之后的步骤也就是上述的评价标准值问题。

(1) 在样本数据集筛选过程中先将全部训练数据集在统计学的概念上分成k个互不相交和相互独立的子集，全部训练数据集用S表示，并且假设S中的训练样例个数为n，那么每一个子集对应为n/k个训练样本比例，相应的子集称作{s1,s2,…,sk}。

(2) 每次从已经分好的互不相交的分子集中里面，随机取出一个作为测试数据集，其他的k-1个视为训练集使用。

(3) 利用工具包函数对k-1个训练集训练学习器模型，随后进行模型输出和假设函数系数输出。

(4) 将得出的模型放到测试数据集上进一步验证，得到分类率。

(5) 通过计算k次，将求得的分类率的平均值，作为该模型或者假设函数的真实分类率。

K折交叉验证能很好地起到参数预测模型的欠拟合和过拟合的平衡作用，可以更好地解释和说明参数模型结果。在Python XGBoost库里，通过CV函数实现交叉验证技术实现。

4.2 与其他分类算法的对比

前文从检验方法的角度，选用了均方根误差、AUC、F1分数和K折交叉验证对预测模型学习效果进行评估和调优。为证实本文选择的该机器学习的优势，选择了两种对随机扰动项不太灵敏的算法NB、LR、两种对异常数据扰动性比较灵敏的算法CART、RF及单一的XGBoost算法作为模型实验的对照。采用鲜明的可视化变现方式，即给出各个算法对应的ROC曲线，在一幅图中可以清晰地看到每个算法的“高下之分”，当一个算法的ROC曲线全部路径在另一条ROC曲线上，基本可以认定前者算法是更优的选择。

图4为XGBoost、NB、LR、CART和RF各分类算法针对本文的犯罪数据集建立的预测模型进行预测结果的ROC曲线路径情况，其中：横坐标为False Positive Rate(反向概率)，纵坐标为True Positive Rate(正向概率)。ROC曲线以越快的速度倾向于坐标的左上角位置，可以认为该算法的分类和回归效果越好。

图4 各算法预测结果的ROC曲线对比图

从图4所示各算法ROC曲线路径分布和走势可以明显看出PCA-XGBoost算法的预测精确度效果优于其他各种分类预测算法。

为了进一步验证和比较各个算法的预测平均准确度以及平均F1分数，对聚合成的48 126个有效数据集进行5次5折交叉验证，分别对应各模型算法建立预测验证和对比。表2可以看到PCA-XGBoost预测准确度明显优于其他四种算法，从各个算法5折平均准确度来看,PCA-XGBoost算法的平均准确率达到88.21%，要优于单一的XGBoost算法(86.53%)，亦远高于其他算法(平均准确率均在80%以下)。如表3所示，从5折F1分数来看,PCA-XGBoost算法的平均F1分数达到85.03%，要优于单一的XGBoost算法(84.23%)，亦远高于其他算法。因此，可以得出PCA-XGBoost算法在预测盗窃类犯罪数量的应用场景之下，将会展现出较大的优势。

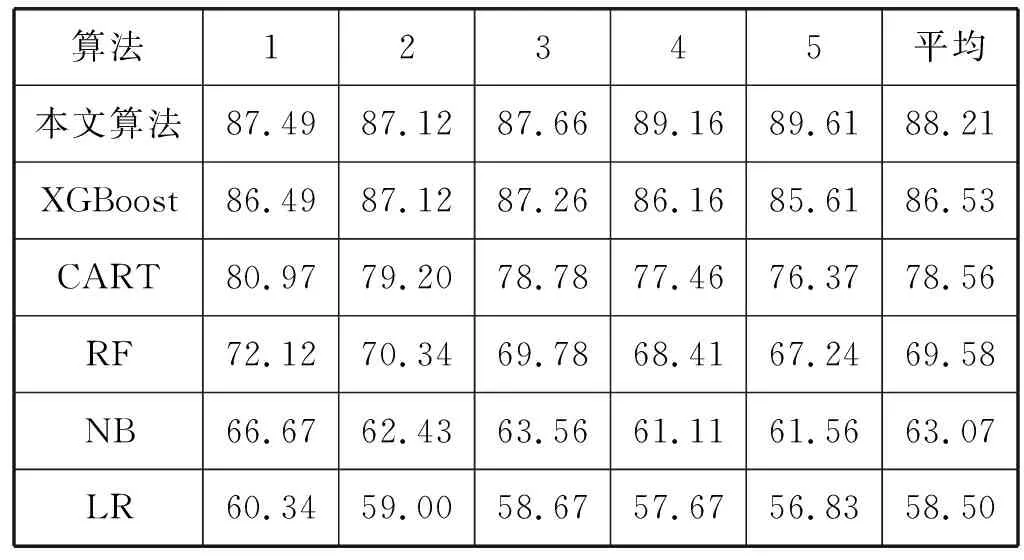
表2 各算法预测准确度对比表(%)

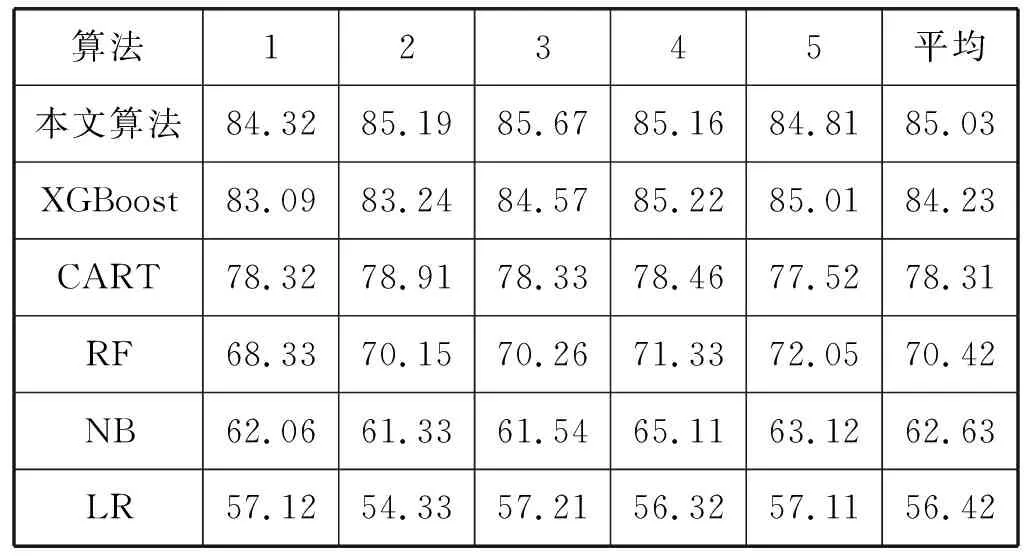
表3 各算法预测F1分数对比表(%)

4.3 预测结果分析

经与测试集数据的对比验证情况来看，基于PCA-XGBoost算法的盗窃犯罪预测模型，不仅在计算效率和速度上有明显优势,而且其预测准确率达到88.21%，其预测F1值为85.03%，高于XGBoost、LR和NB等其他一些常用的分类模型。因此,该预测模型能够有效地揭示盗窃犯罪在相应时间和空间下的数量及其变化情况，其预测准确度是非常具有实际指导意义的，在实际警务工作中有较大的推广价值。

5 结 语

本文以2017年美国芝加哥市的盗窃犯罪的911报警数据集作为样本数据，建立了具有较佳性能且适用于芝加哥市盗窃类犯罪的犯罪预测模型。通过多种检验方法得出该PCA-XGBoost算法模型具有较高的准确率。另一方面，通过与其他分类算法模型进行横向对比实验表明：PCA-XGBoost模型对样本市的盗窃犯罪发生数量的预测准确度明显高于其他类型的分类预测模型，其预测准确率达到88.21%，其F1分数可达85.03%。可以预见，该算法模型将在当地警方针对盗窃犯罪的防控和打击工作中发挥重要作用。

需要注意的是，本文研究的是盗窃犯罪只是诸多犯罪类型的一种。不同地域、不同犯罪类型在时间和空间上都可能大相径庭。因此，在未来针对不同类型犯罪预测模型的构建中，不仅要结合报警数据，还有必要考虑当地实际的犯罪数据进行深度学习，尤其是要在特征向量的提取方面，将与犯罪人、被侵害人(地)有关复杂特征数据一并考虑。这样开发的预测模型才能更准确和快捷，这也必然是犯罪预测研究未来的热门研究方向之一。