OOPN网精细化操作及在垃圾分类建模中的应用
王兆诚 夏传良 张 玮 王壮壮
(山东建筑大学计算机科学与技术学院 山东 济南 250101)
0 引 言
在日常生活中,垃圾分类处理逐渐被政府和人们重视并实践应用,但人为垃圾分类需要公众有高度的自觉意识,收效甚微,于是智能垃圾分类拣放机应运而生,为了加快拣放机垃圾分类处理的速度并降低功耗,有必要对这类系统进行建模研究和管理。智能垃圾分类的过程有很明显的模块化、功能化特征,如垃圾识别、垃圾分拣、垃圾对应回收和垃圾运输处理等。Petri网作为一种系统模型,一般对系统及行为进行统一考虑,但不能体现出系统功能模块的划分。而利用面向对象的相关定义对系统进行功能、模块的划分,将整个复杂系统的建模过程有效地划分为多个简单子系统,并相应进行建模研究正是面向对象Petri网建模技术的突出优势所在[1]。
本文选择面向对象Petri网作为智能垃圾分类拣放机系统的建立模型,用于研究、分析的工具,鉴于一次性建模存在复杂性、不确定性因素大的问题,首先利用OOPN建立原始系统粗略、大体的模型,然后再运用相应的精细化方法对大概的模型进行精细化处理,从而可得更加详细、精确的目标网系统模型。
为了使复杂业务处理过程的建模变得简单、清晰,那绝对必要的是采用精细化方法来把复杂的主过程进行分解,形成更小的子过程,这样才能有效降低复杂度,也就是所谓的“分而治之”策略[2]。潘卫军等[3]对机坪内各交通模块进行精细化建模,采用基本网模型的精细化代替方法,清晰自然地得到机坪运行过程的全局着色Petri网模型;Xia等[4]提出了PRES+(Petri net based Representation for Embedded Systems),即基于Petri网表示的嵌入式系统模型的细化方法,使得运用Petri网对嵌入式系统建模时的复杂度降低,效率增高。
除此之外,不少学者对面向对象Petri网的性质及精细化设计也做了研究。文献[5]给出了扩展面向对象Petri网(EOOPN)的定义及性质,如封装性、抽象性;文献[6]研究了将面向对象的继承性以及与之紧密联系的多态性引入OOPN网;文献[7-8]研究了面向对象Petri网的信息交互性,并基于OOPN对高速铁路行车指挥系统进行建模;文献[9]给出了EOOPN模型中的构件细化及其一种类型,指出精细化的主要思想是将抽象的库所(ABP)、变迁(ABT)和标识(Token)精细化为构件子网或更详细的抽象库所、变迁和标识;文献[10]详细给出了EOOPN中的其他三种构件细化方法(ABP细化、ABT细化和Token细化),提出了结构良好性的定义,也证明了细化后仍保持结构良好性。上述工作虽然研究了OOPN的一些性质和精细化操作方法,但对OOPN的活性、有界性及精细化后对该性质的保持未做详细研究说明。
本文提出了一种面向对象Petri网的类网精细化方法并研究了如何使精细化后的目标网系统保持原有的活性、有界性。首先,根据相关条件要求,对原始OOPN系统进行类网精细化操作,此操作完成后,便可得到更细致的期望目标网系统,则该系统仍能保持活性、有界性的条件是:当且仅当原始OOPN系统和进行替换的闭类网系统都是活的、有界的。这对于Petri网复杂大系统的分析具有重要的指导意义,值得一提的是,本文给出的OOPN类网精细化操作模型绝不仅仅可用来描述和处理“智能垃圾分类拣放”的具体过程,可覆盖柔性制造系统中诸如“某车间的若干台机器为其生产某些部件”的问题类。
1 基本定义和符号
本节给出面向对象Petri网及系统的相关定义和示例,以及系统活性、有界性的定义。
定义1设六元组N=(P,T,F,Q,G,W)是一个OOPN模型:
P={p1,p2,…,pm}是一确定库所集合,P≠∅;
T={t1,t2,…,tm}是一确定变迁集合,T≠∅;
F={FI,FO}是网N的流关系,FI⊆(T×P或T×Q或G×Q)是一确定的输入弧集合,FO⊆(P×T或Q×T或Q×G)是一确定的输出弧集合;
Q={q1,q2,…,qm}是一确定非空的消息库所集合,分为输入消息库所QI和输出消息库所QO,从网关接收到消息的为输入消息库所,向网关发送消息的为输出消息库所;
G={G1,G2,…,Gm}是对象间的网关集合;
W:F→{1,2,3,…}称为权函数;
Σ=(N,M)称为一个OOPN系统,M:P→{0,1,2,…}和QI→{0,1,2,…}是Σ的一个标识,其中,M0是初始标识。
用示例来阐明这部分提出的模型定义,如图1所示。

图1 一个OOPN示例
图1中:P={p1,p2};T={t1,t2};
FI={(t1,p2),(t2,p1),(t1,q2),(G1,q1)};
FO={(p1,t1),(p2,t2),(q1,t2),(q2,G2)};
G={G1,G2};QI={q1,q3};QO={q2,q4};
M0=[M(p),M(q)]=[1,0,0,0,0,0];
权函数W未标识出的默认为1。
其中,消息库所Q用椭圆形表示,它类似于对象与外界的通信窗口;通信网关G用粗实线表示,它与变迁类似,用来实现对象间的连接;抽象和封装好的类用圆角矩形来表示;类的“实例”数目用Petri网中的标识来表示[11]。
定义2设N=(P,T;F,Q,G,W)是一个OOPN模型,Σ=(N,M0)是一个OOPN系统,M∈R(M0)。
1) 变迁t∈T,当·t∩Q=Φ时,t可称为在M下使能的充分必要条件为:
∀p∈P:M(p)≥W(p,t)
(1)
满足式(1)记作M[t>。
当t∩Q≠Φ时,t可称为在M下使能的充分必要条件为:
∀p∈P∧∀q∈Q:M(p)≥W(p,t)∧M(q)≥W(q,t)
(2)
满足式(2)记作M[t>。
2) 变迁t可以发生的条件为:t能够在标识M下使能;发生的结果为:M→M′。
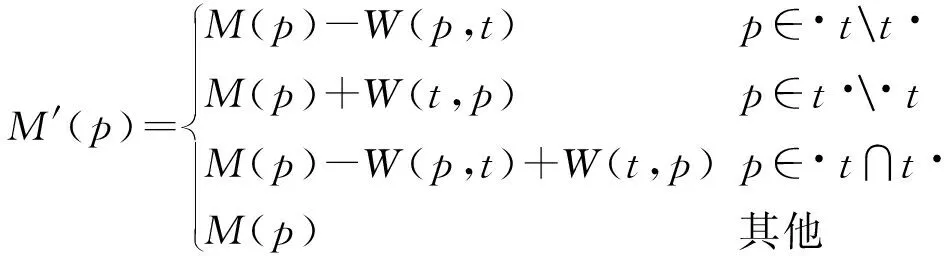
(3)
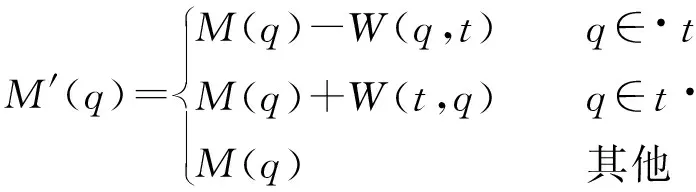
(4)
定义3设Σ=(N,M0)是一个OOPN系统:
1) 变迁t∈T是活的,当且仅当∀M∈R(M0),∃M′∈R(M),M′[t>;
2)Σ是活的,当且仅当∀t∈T,t是活的。
定义4设Σ=(N,M0)是一个OOPN系统:
1) 库所p∈P是有界的,当且仅当∃k1>0,使得M(p)≤k1,∀M∈R(M0);消息库所q∈Q是有界的,当且仅当∃k2>0,使得M(q)≤k2,∀M∈R(M0)。
2)Σ是有界的,当且仅当∀p∈P∧∀q∈Q,p和q都是有界的。
定义5设N=(P,T;F,Q,G,W)和Na=(Pa,Ta;Fa,Qa,Ga,Wa)是两个OOPN网,若满足:
1)Pa⊆P,Ta⊆T,Qa⊆Q,Ga⊆G且Pa≠∅,Ta≠∅,Qa≠∅;
2)Fa=F∩((Pa×Ta)∪(Ta×Pa)∪(Qa×Ta)∪(Ta×Qa)∪(Ga×Qa)∪(Qa×Ga))。
则称Na是N的一个OOPN子网,或者称为类网,记为CNa。
为了更形象准确地定义类网,规定:
在类网中,消息标识只能从输入消息库所进,从输出消息库所出,不可逆。
定义6类网精细化操作Re f(pA,CNa):将面向对象Petri网N=(P,T;F,Q,G,W)中的库所pA精细化为一个类网CNa=(Pa,Ta;Fa,Qa,Ga,Wa)(用类网CNa来替换pA),得到OOPN模型,N′=(P′,T′;F′,Q′,G′,W′)。其中:
1)P′=(P-{pA})∪Pa;
2)T′=T∪Ta;
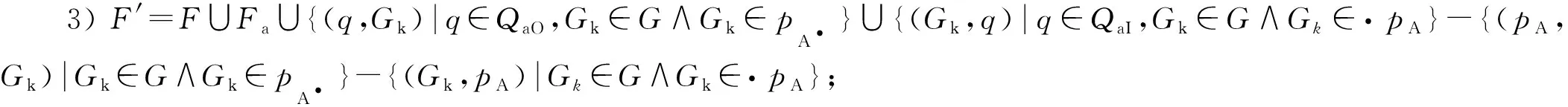
4)Q′=Q∪Qa;
5)G′=G∪Ga;
6)W′(x,y)=
(5)
(6)
式中:M(PpA)为M中去掉pA所对应的分量以后的向量,ϑA是Ma的零向量。
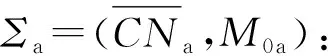
2 OOPN的类网精细化操作性质分析
本节先提出关于OOPN系统的活性、有界性定理,再提出经过类网精细化操作后系统仍保持活性、有界性的充要条件。
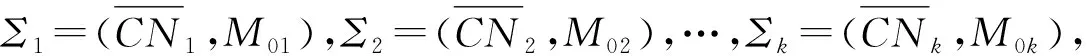
证明:(1)p⟸q。
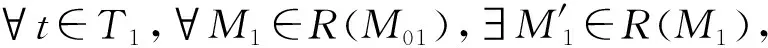
(2)p⟹q。

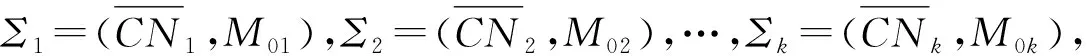
证明:(1)p⟸q。
∵ 系统Σ1是有界的,则∀p∈P1∧∀q∈Q1,∃k1>0使得M1(p)≤k1∧M1(q)≤k1,∀M1∈R(M01);同理,Σ2有界的,则∀p∈P2∧∀q∈Q2,∃k2>0使得M2(p)≤k2∧M2(q)≤k2,∀M2∈R(M02)。此类推,令k=max{k1,k2,…,kk},则∀p∈P∧∀q∈Q,M(p)≤k∧M(q)≤k,∀M∈R(M0),∴ OOPN系统Σ=(N,M0)是有界的。
(2)p⟹q。
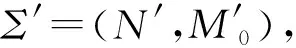
证明:(1)p⟸q。
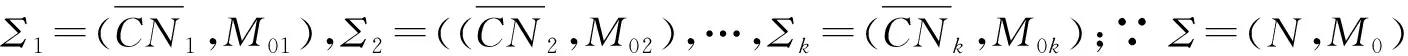
(2)p⟹q。
显然,∀M(PpA)*∈R(M(PpA)),使得(M(PpA)*[t>)。因为M(PpA)0是在(N,M0)上的投影,假设M(PpA)0[σ>M(PpA)[σ*>M(PpA)*,σ,σ*∈T,现在加入中的变迁(或变迁步)σa,可得σ′,σ″∈T″。又因为OOPN系统是活的,结合定义6可知,并且M(PpA)是M′在(N,M0)的投影,M(PpA)*是M*′在(N,M0)上的投影,所以对应于使得对应于∀M(PpA)*∈R(M(PpA)),∀M*′∈R(M′),(M(PpA)*[t′>)⟹(M*′[t>),所以不活,矛盾。因此可以得出从中通过抽象化操作获得的系统(N,M0)和从中通过抽象化操作获得的闭类网系统都是活的。因为{p|p∈Pa∧Ma(p)>0}⊆{p|p∈P′∧M′(p)>0},则从OOPN系统中通过类网精细化操作所得到的系统Σ=(N,M0)和闭类网系统都是活的。
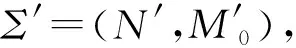
证明:(1)p⟸q。
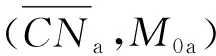
(2)p⟹q。
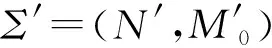
3 应用实例
本节将提出的OOPN类网精细化操作方法应用到对智能垃圾分类拣放系统的建模分析,在准确反映系统工作流程的同时,也有利于工作人员对该系统进行研究和管理,说明了该方法的可行性和有效性。
智能垃圾分类拣放机模型主要由传送带,智能扫码识别系统和拣放控制系统三部分组成。贴有专用二维码的垃圾袋(内含垃圾)通过传送带运输,到达扫码区,扫码区感应到垃圾,扫描仪自动扫码,识别垃圾袋中所装垃圾为可回收垃圾、有毒有害垃圾、干垃圾或湿垃圾中的一种,继而拣放控制系统工作,对应垃圾仓门打开,机械臂自动将垃圾拎入对应仓内,继续传送后续垃圾进行处理。
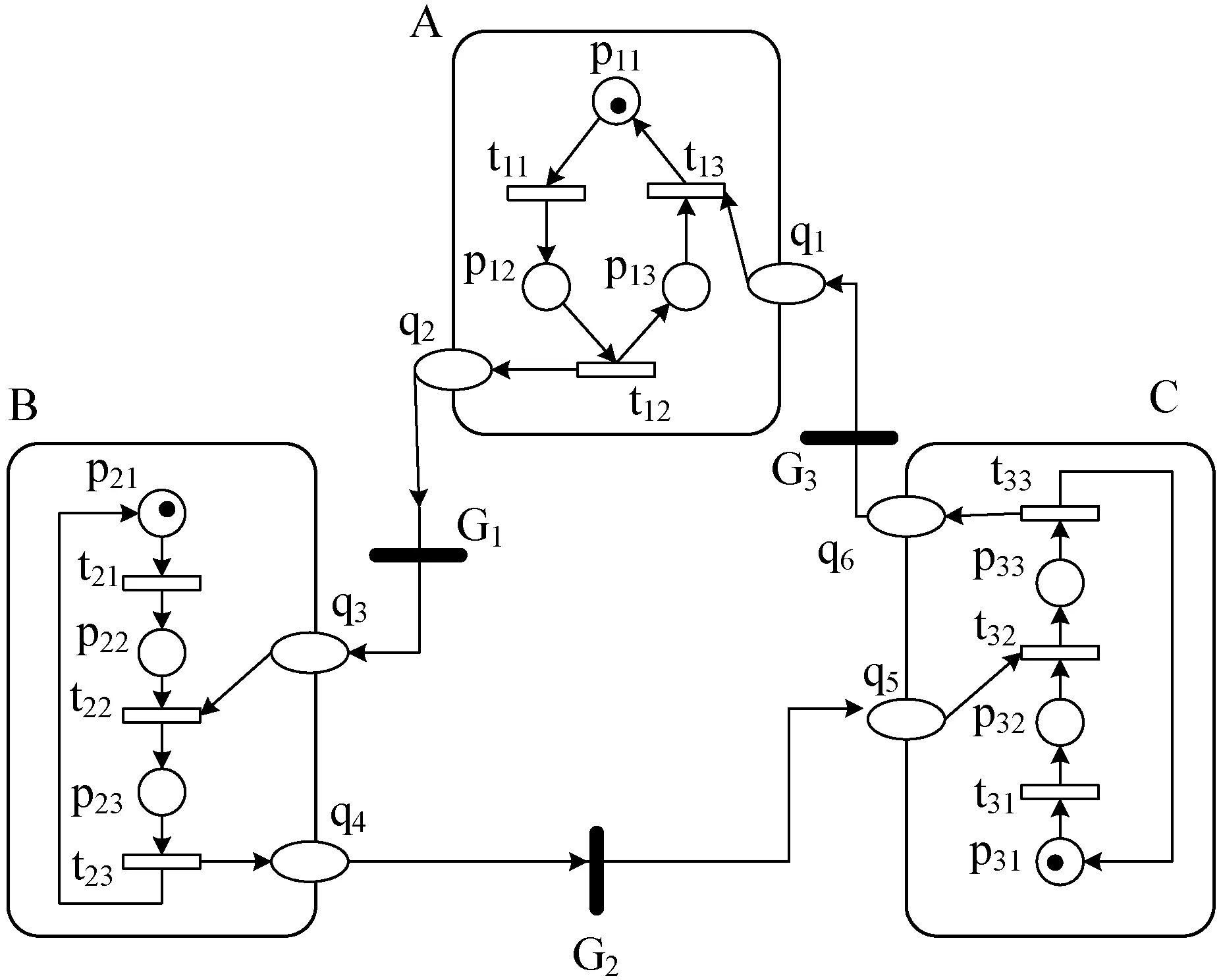
首先给出粗略OOPN系统模型Σ=(N,M0)(见图2),然后用类网CNa(见图3)对粗略模型中的pA进行细化。闭类网系统Σa如图4所示。此时,精细化后的完整的OOPN系统模型已得到(见图5)。同理,根据具体情况,还可以对图2中的B、C先建立粗略模型,再进一步细化。

图2 Σ=(N,M0)
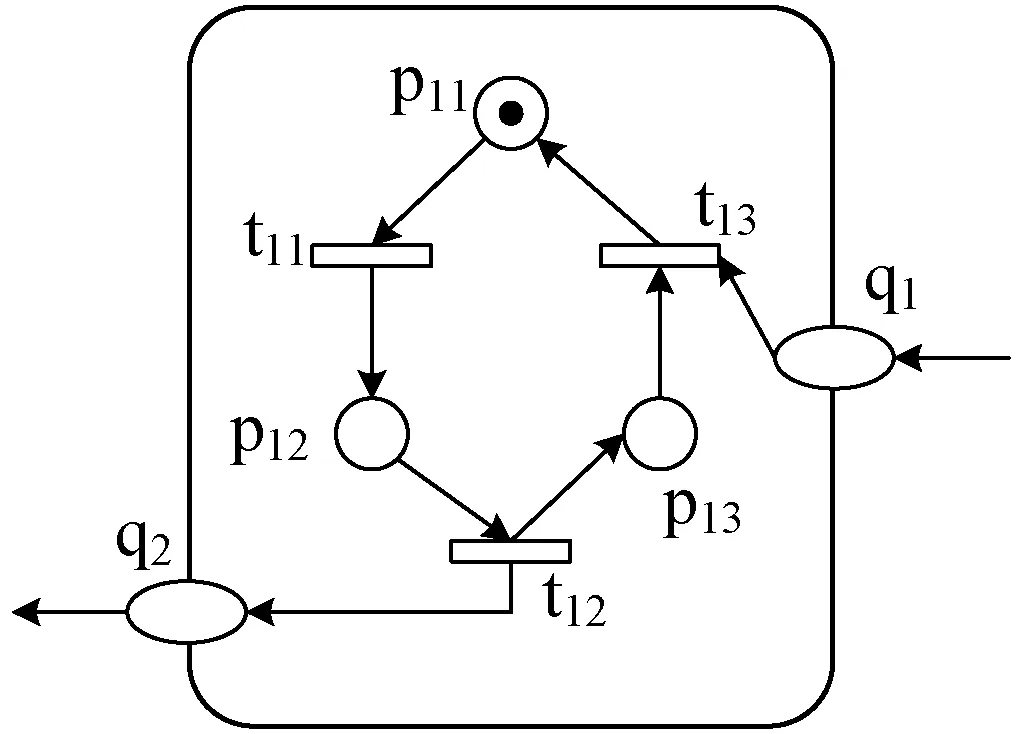
图3 类网CNa
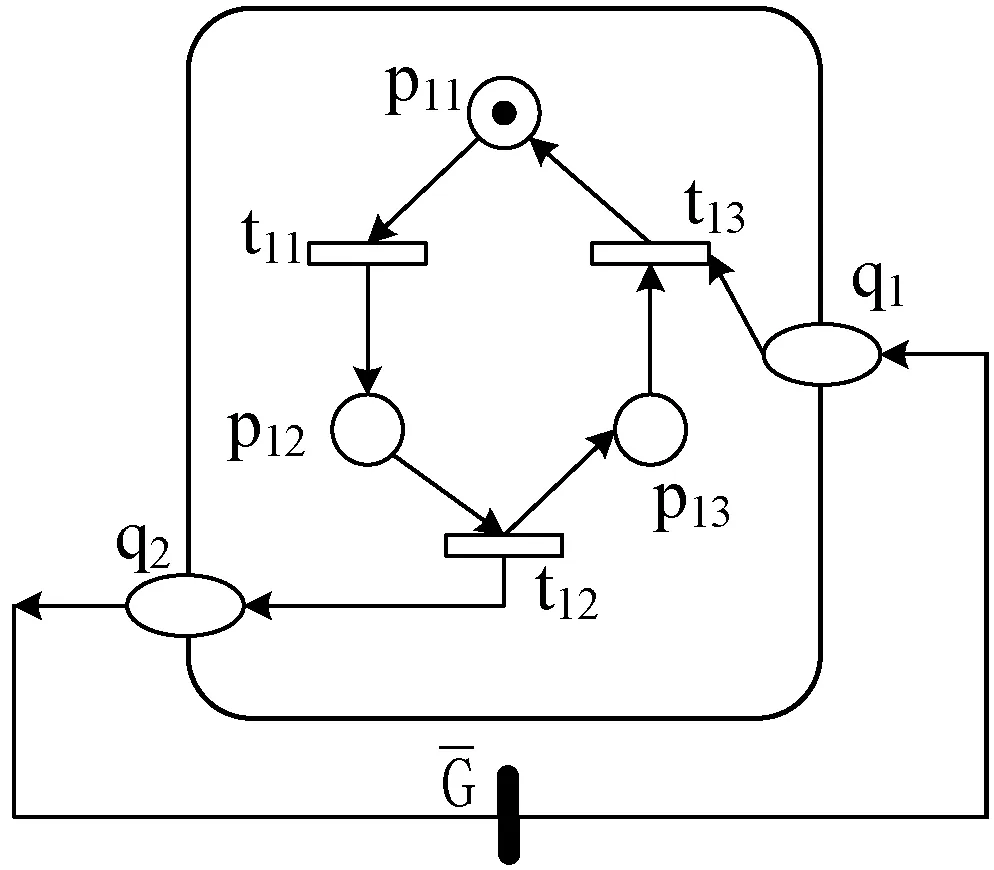
图4 闭类网系统
图
图2中图例的含义如下:
pA:传送带 G3:通信网关
B:扫描识别区 C:分类拣放区
p21:空闲 p31:空闲
p22:等待扫码许可 p32:等待拣放许可
p23:扫码 p33:拣放垃圾
t21:申请扫码 t31:申请拣放
t22:获得扫码许可 t32:获得拣放许可
t23:完成扫码 t33:完成拣放
q3、q4:消息库所 q5、q6:消息库所
G2:通信网关 G3:通信网关
图2包括B:扫码识别区、C:分类拣放区两个对象。图3、图4中图例含义如下:
p11:空闲 t11:感应到垃圾
p12:传送垃圾 t12:到达扫描
p13:暂停 t13:运行通告
q1、q2:消息库所 G1:通信网关
图5中图例的含义同图2、图3中相应图例的含义。包含A:传送带、B:扫码识别区、C:分类拣放区三个对象。
开始时,传送带转动,扫码区感应到有垃圾时,通过G1向B发送消息,使其获得扫码许可,从而进行扫码得到垃圾类别,完成扫码后通过G2向C发送消息,使其获得分类拣放许可,从而将垃圾按类别拣放处理,拣放完成后,通过G3再向A发送消息,告知垃圾拣放完毕,可继续运行。
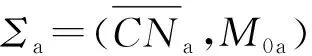
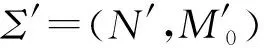
实际上,对于OOPN系统Σ=(N,M0),初始标识M0=(M0(pA),M0(p21),M0(p22),M0(p23),M0(p31),M0(p32),M0(p33),M0(q3),M0(q4),M0(q5),M0(q6))=(1,1,0,0,1,0,0,0,0,0,0),易知Σ=(N,M0)是活的。
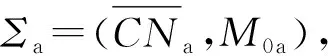
4 结 语
本文就面向对象Petri网的活性、有界性给出较完备的定义并提出OOPN类网精细化操作及其动态性质保持问题,然后利用提出的精细化操作对智能垃圾分类拣放系统进行建模分析,并证明了活性、有界性保持良好,进一步说明了该方法的实际价值。本文的结果为OOPN应用于复杂大系统的分析管理提供了有力支持。经精细化后得到目标网保持可回复性、公平性等性质是下一步的研究重点。

