基于LS-CSO优化MWLS-SVM的SO2排放浓度软测量建模
梁伟灿 周 宾 王汗青
(东南大学能源与环境学院 江苏 南京 210000)
0 引 言
近年来,煤炭燃烧所引起的一系列大气污染问题引起了社会高度关注,国家颁布了一系列节能减排环保规划,不断加强对燃煤电厂各项大气污染物排放限制,尤其是重点地区的燃煤电厂,因此,燃煤电厂不断完善尾部烟气除尘、脱硝以及脱硫等方面工作。针对尾部烟气脱硫问题,石灰石-石膏湿法脱硫技术(WFGD)已经成为了我国燃煤锅炉主要的脱硫手段,并借助烟气连续排放检测系统(CEMS)对燃煤电厂脱硫系统二氧化硫排放进行实时监测[1],但这一类监测仪表普遍存在安装维护复杂、工程造价昂贵等问题。为了解决这些问题,大量研究提出基于机理分析或历史运行数据建模的方式实现二氧化硫排放软测量,这为脱硫系统参数快速调整提供可靠依据,保证了二氧化硫可以实现超低排放[2]。
在工业现场应用中,软测量技术是通过建立易测量且准确度高的辅助变量,如温度、压力、浓度和流速等,与待测变量之间的数学模型,以期能够获得待测变量的精确预测[3]。近年来,针对WFGD系统建模的软测量主要包括物理建模[4]、数据建模[5-6]以及数据与物理混合建模[7-8]三种方式。针对应用于复杂工业场景,最小二乘支持向量机[9](Least Squares Support Vector Machine,LS-SVM)通常仅仅考虑模型样本输入的噪声和异常值问题,对LS-SVM训练样本进行样本加权处理,解决LS-SVM模型学习效果较差的问题[10],如赵超等[11]通过采用指数分布加权规则对LS-SVM建模样本进行权重分配,提高了模型抵抗噪声和异常值的能力,但对于非线性系统的软测量而言,软测量各辅助变量对结果影响存在差异,而LS-SVM建模过程中通常会对训练样本进行归一化处理,以期望能够消除各辅助变量数值分布不均匀的问题[12],但同时会导致各辅助变量的权重相同,无法区分各辅助变量对结果的差异化影响,因此导致模型效果较差[13]。
然而,LS-SVM软测量建模过程中各辅助变量权重以及超参数惩罚因子C和高斯核宽系数σ很难通过先验信息进行确定,属于大规模优化问题,因此采用传统网格搜索法对超参数以及辅助变量权重进行确定必定会存在搜索速度慢、无法确定最优参数等缺点[14]。近年来,元启发式优化算法在大规模优化问题上取得了巨大的进步[15],因此采用元启发式寻优算法解决模型超参数和辅助变量权重的选择面临高维大规模优化的困境是一条行之有效的途径[16]。其中,基本竞争粒子群(Competitive Swarm Optimizer,CSO)在大规模优化问题上取得了较好的表现,但竞争粒子群算法存在多样性低的问题,导致算法在搜索速度和精度表现较差。因此,通过改进种群划分规则、自适应调整搜索参数以及引入胜利粒子更新策略三种方式[17-21]来解决竞争粒子群种群多样性问题。
针对上述LS-SVM建模过程的问题,本文在DWLS-SVM[9]基础上加入特征加权,提出一种混合加权最小二乘支持向量机(Mixed Weight Least Squares Support Vector Machine,MWLS-SVM),同时提出一种局部搜索竞争粒子群(Local Search Competitive Swarm Optimizer,LS-CSO)对特征权重和模型参数进行同步优化,最终形成了一套基于LS-CSO优化MWLS-SVM的软测量建模方法,将其应用于湿法烟气脱硫系统SO2排放浓度软测量中,实验结果表明该建模方法能够提高模型的逼近能力、泛化能力和预测精度。
1 建模方法
1.1 最小二乘支持向量机
最小二乘支持向量机通过非线性变换,将非线性样本空间S={(xi,yi),x∈Rn,y∈R,i=1,2,…,m}映射到高维特征空间S′={(φ(xi),yi),i=1,2,…,m}[9],从而以结构风险最小化为原则确定模型参数wT和b来拟合高维特征空间中的函数y=wTφ(x)+b,其等价于求解下述优化问题:
(1)
s.t.yi=wT·φ(xi)+b+eii=1,2,…,m
(2)
式中:R为模型结构风险;C为正则化参数;ei为样本估计误差。通过引入拉格朗日函数,上述问题可变换为:
(3)
(4)
最终LS-SVM训练问题简化为线性方程求解模型参数α和b,拟合方程为:
(5)
1.2 混合加权最小二乘支持向量机
为了解决软测量建模中噪声、异常值以及特征差异化影响的问题,一方面,通过对训练样本引入加权系数v={vi,i=1,2,…,n}间接优化模型损失函数,降低噪声和异常值对软测量模型影响;另一方面,对各维特征引入加权系数g={gi,i=1,2,…,n}直接改变核函数,实现各维特征差异化,提高模型学习能力,最终模型求解线性方程如下:
(6)
假设核函数为高斯核函数,则有:
(7)
式中:i=1,2,…,m,j=1,2,…,m,m为样本数,n为样本输入特征数。根据文献[9]确定经验项加权系数vi,本文不做赘述。
2 算法设计
2.1 基本竞争粒子群
基本竞争粒子群(CSO)是根据生物学中的优胜劣汰竞争机制对粒子群算法进行的改进[22],但在概念上有很大的不同,不同于传统粒子群算法粒子更新机制,竞争粒子群采用竞争淘汰机制进行粒子更新,即胜利粒子决定了失败粒子位置和速度的更新。
一般地,考虑下述优化问题:
minf=f(p)
(8)
式中:p∈RN,N是搜索空间的维度。
在搜索空间内,原始粒子群P(t),种群数量为M,每个粒子pi(t)=[pi,1(t),pi,2(t),…,pi,N(t)]对应了上述问题的一个候选解。在每代进化更新过程中,将粒子群随机分成数量相等的两部分粒子群PA(t)和PB(t),分别从两粒子群中取出一个粒子根据适应度大小进行竞争,胜利粒子直接进入下一代,失败粒子通过向胜利粒子学习并更新粒子速度和位置,第k轮竞争的更新公式如下:
vl(k,t+1)=R1(k,t)·vl(k,t)+
R2(k,t)·(pw(k,t)-pl(k,t))+
η·R3(k,t)·(pmean(t)-pl(k,t))
(9)
pl(k,t+1)=pl(k,t)+vl(k,t+1)
(10)
式中:pw(k,t)和pl(k,t)分别为胜利粒子和失败粒子位置,vl(k,t+1)为失败粒子更新后速度,t为当前迭代代数,随机向量R1(k,t)、R2(k,t)、R3(k,t)∈[0,1]N,pmean(t)为当前粒子群的平均位置,η是pmean(t)影响控制因子。
2.2 局部搜索竞争粒子群
竞争粒子群在每次迭代更新的过程中,仅仅只考虑了失败粒子的位置和速度的更新,相当于只利用一半种群在搜索空间内进行探索开发,失去了粒子群算法种群多样性的特点,这样使得种群的全局搜索性和收敛速度降低,并且当胜利粒子集中在某个局部最优点处时,算法可能会导致陷入局部最优解。
在竞争粒子群基础上,考虑胜利粒子缺少更新导致种群搜索性下降的问题,采用邻域随机粒子与胜利粒子进行二次竞争,将局部搜索引入竞争粒子群,对胜利粒子的位置和速度进行更新,提出一种局部搜索竞争粒子群(LS-CSO)算法,算法流程如图1所示。
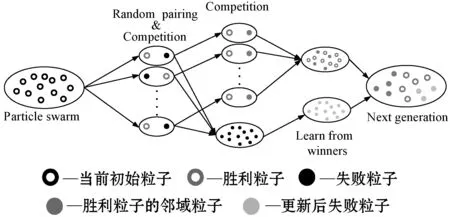
图1 局部搜索竞争粒子群流程
更新公式如下:
pn(k,t)=pw(k,t)+λ·R4(k,t)·(pupper-plower)
(11)
(12)
(13)
式中:pw(k,t)和pn(k,t)分别为胜利粒子和对应邻域粒子位置,pupper和plower分别为粒子搜索空间的上下限,随机向量R4(k,t)∈[-1,1]N,局部搜索范围控制因子λ∈[0,1],随着λ值增加,邻域搜索范围增大,当λ=1时,邻域随机搜索变换为全局随机搜索。
2.3 邻域搜索竞争粒子群算法性能验证
为了探究LS-CSO算法的搜索性能,将采用CSO算法与LS-CSO算法分别对六个测试函数进行寻优测试对比,这六个测试函数分别为Levy Function(100D)[23]、Bohachevsky Function(2D)[24]、Zakharov Function(50D)[25]、Six-hum Camel Function[26]、De Jong Function N.5(2D)[25]、Powell Function(100D)[25]。为了保证测试实验真实反映算法的搜索性能,除了算法本身流程差异外,设置统一公共初参数(随机初始位置P(0)、初始速度V(0)=0.1、均值影响因子η=0[23]以及最大迭代次数)以及过程随机数(R1,R2,R3),局部搜索范围控制因子λ根据经验选取最优值,对各个函数进行50次独立测试实验,记录迭代过程算法最优值以及最终寻优值,统计各次实验最终寻优值的平均值及标准差,参数设置及仿真结果如表1所示,图2为各测试函数的收敛曲线。
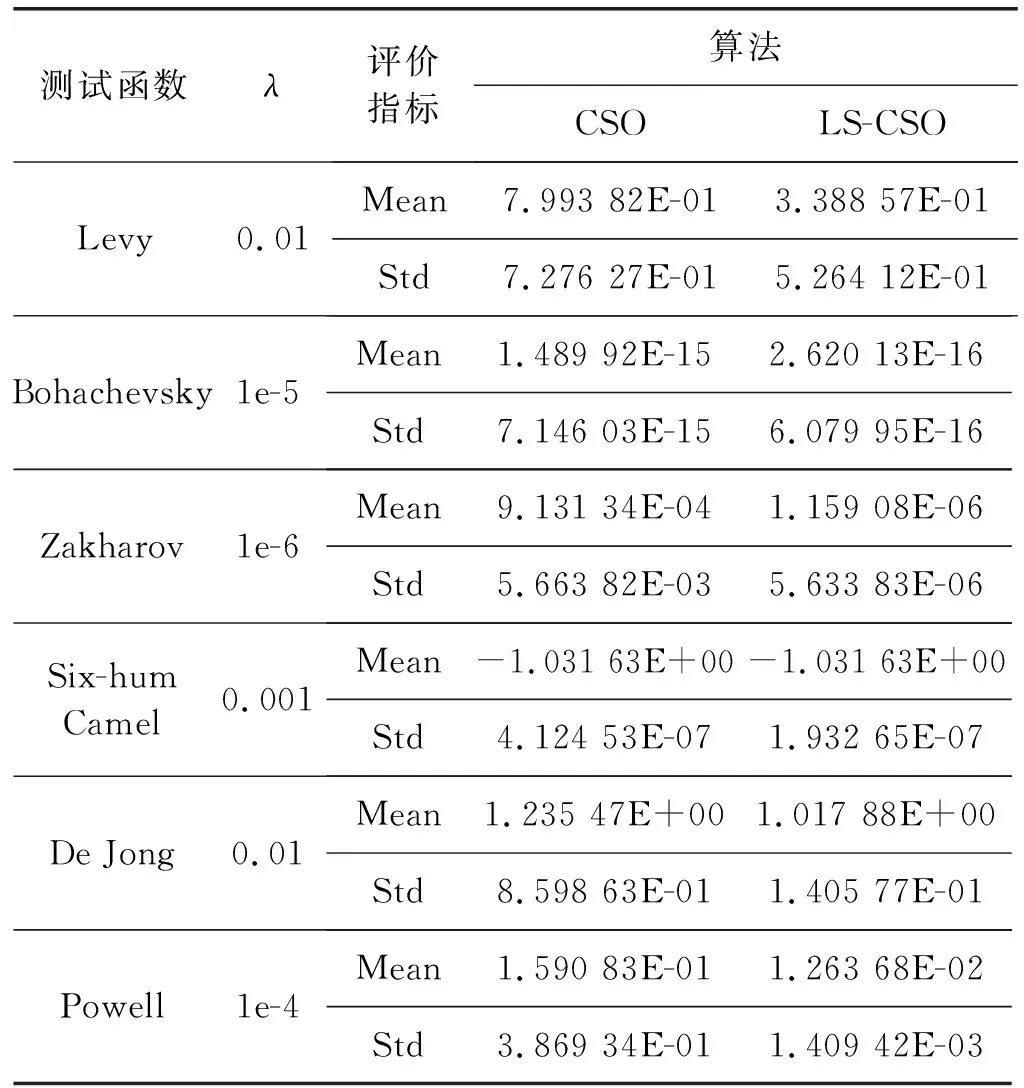
表1 优化仿真实验结果
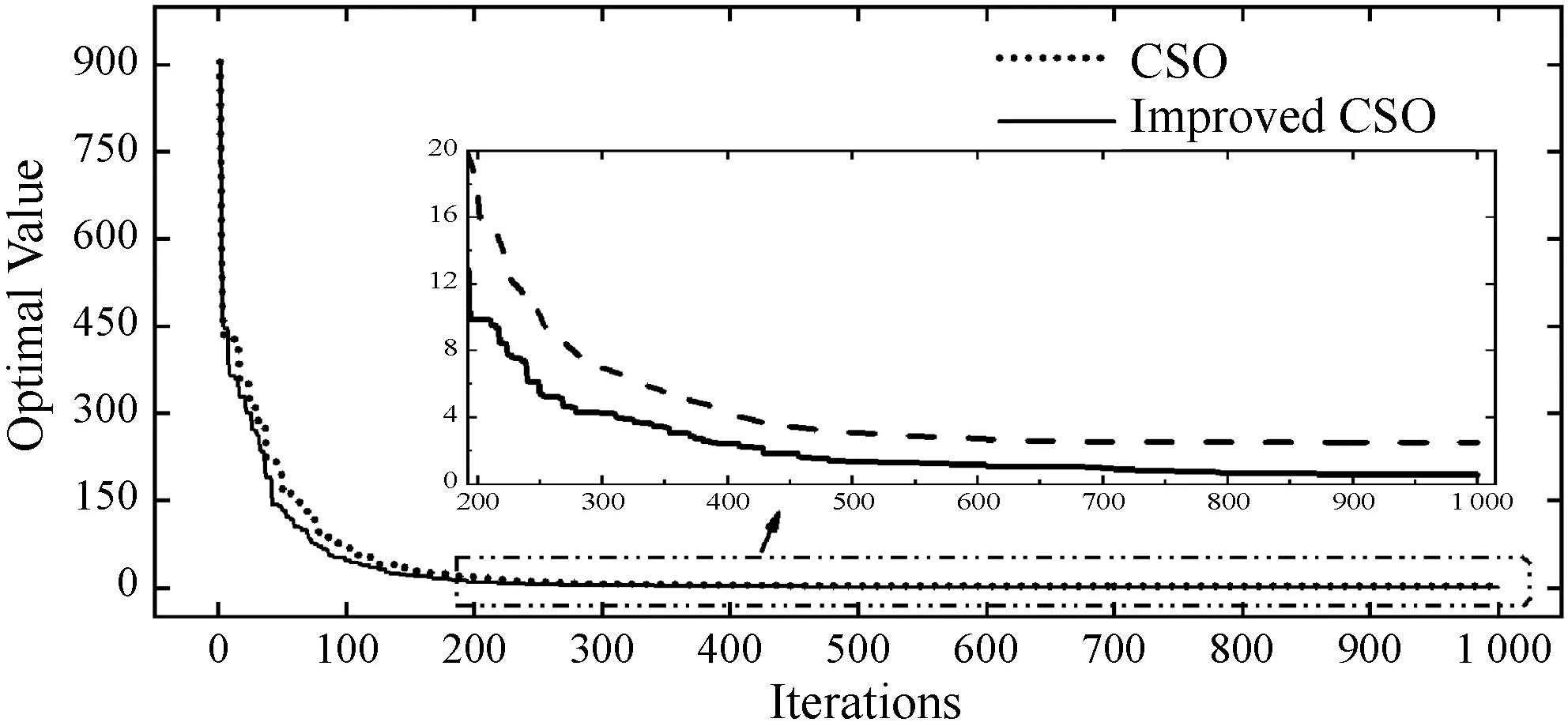
(a) Levy function
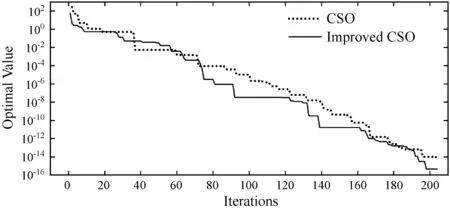
(b) Bohachevsky function
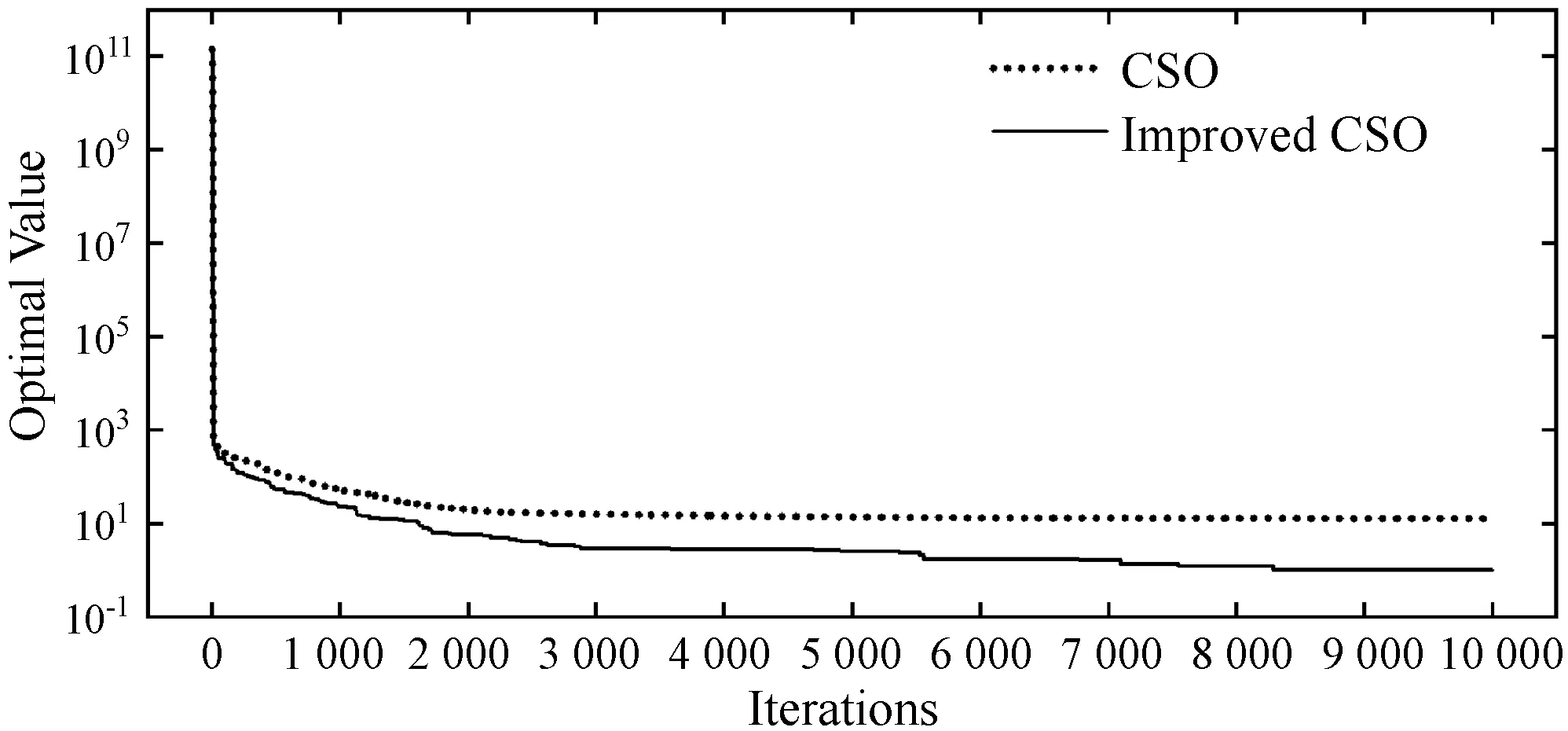
(c) Zakharov function
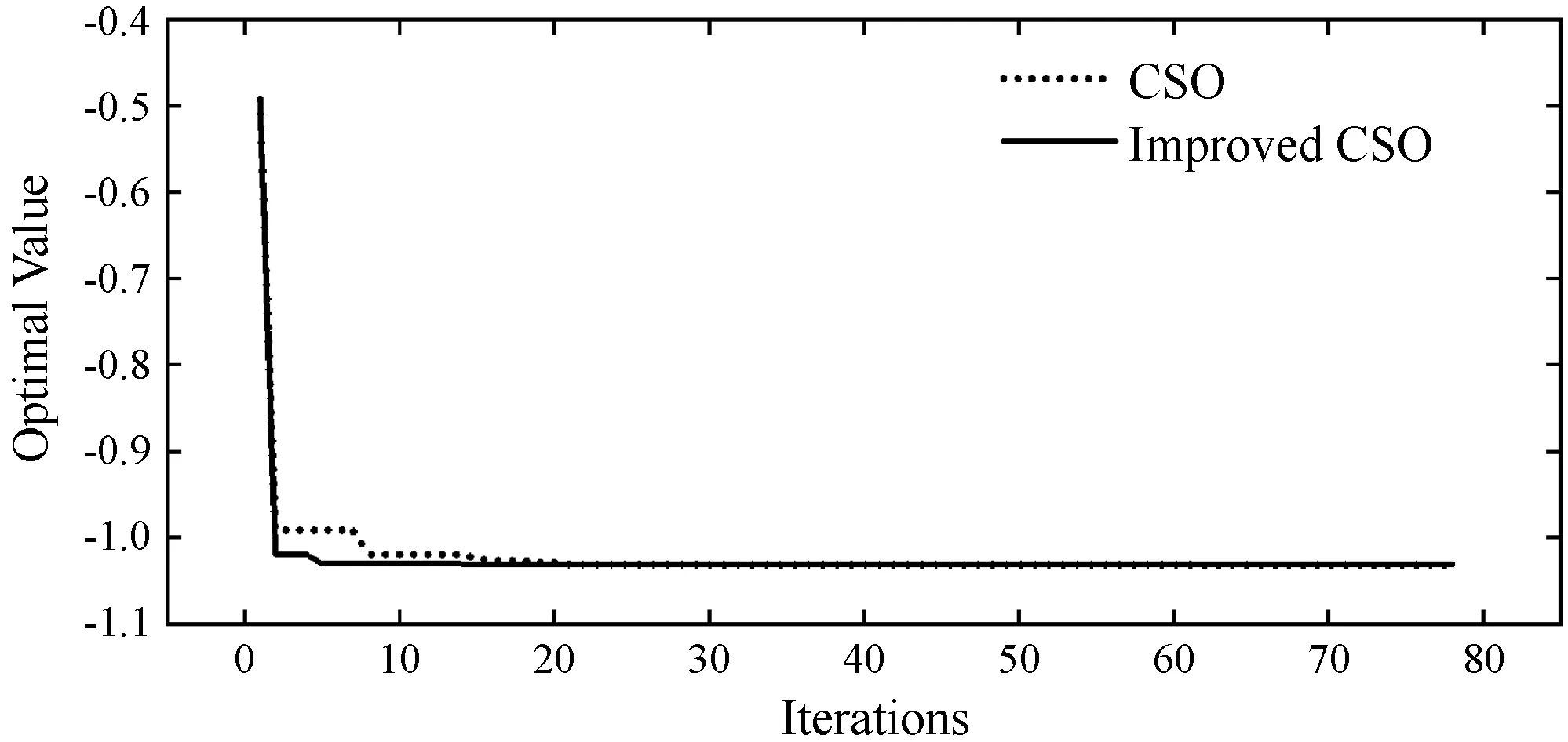
(d) Six-hum camel function
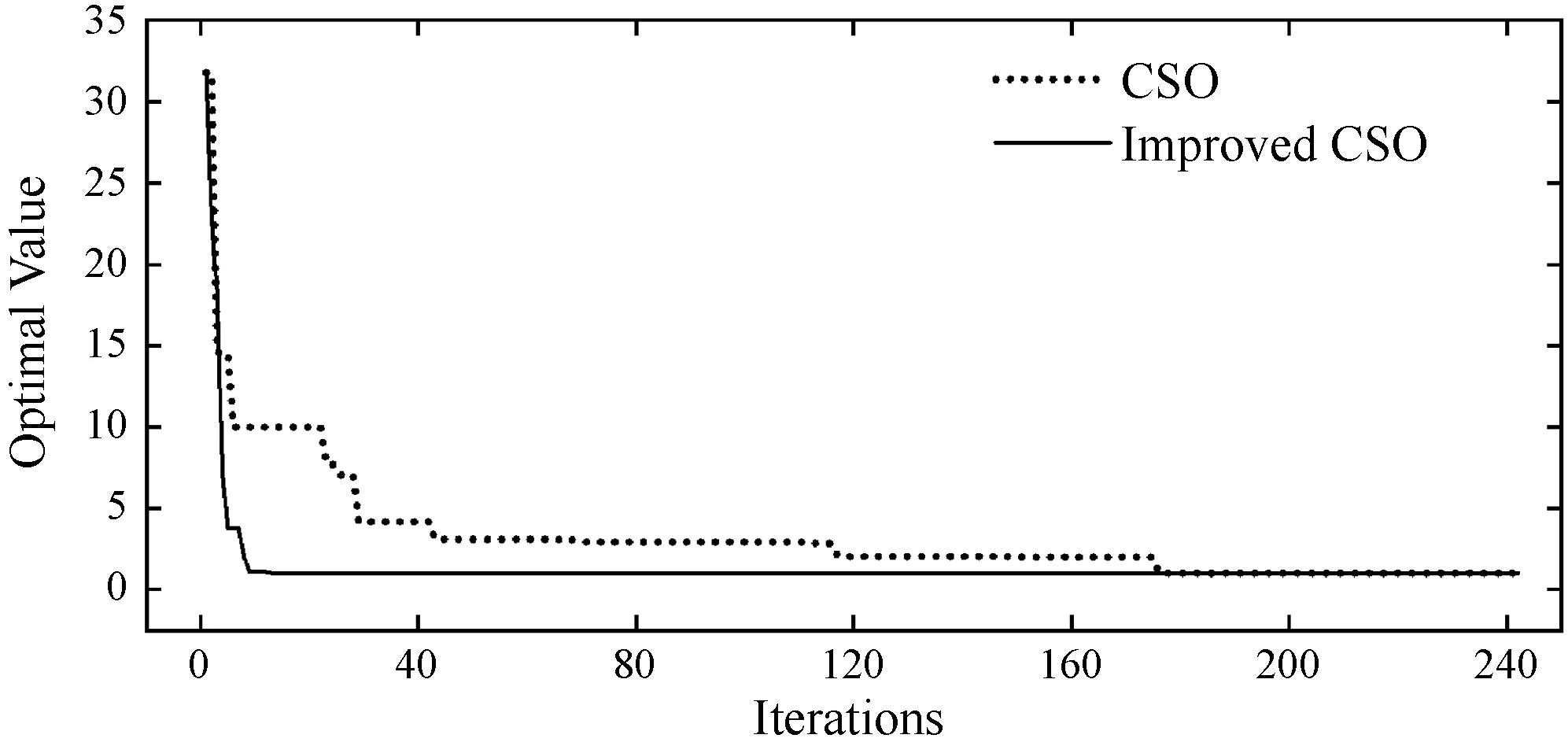
(e) De Jong function

(f) Powell Function图2 各测试函数收敛曲线
根据表1的最终统计结果,在所有测试函数上,LS-CSO算法均比原始CSO算法取得了更加优秀的寻优表现,特别对于Zakharov Function,在相同迭代代数下,LS-CSO算法相较于原始CSO有了更大的提升。另外,De Jong Function存在多个局部最优解,各局部最优解附近呈现陡坡式下降,这导致原始CSO算法极易收敛至局部最优,而LS-CSO算法都能够收敛至全局最优,这很好地验证了前文所提及的“当胜利粒子集中在某个局部最优点处时,算法可能会导致陷入局部最优解”的问题,而LS-CSO算法的确很好地解决了这一问题。
对于原始CSO算法而言,当搜索前期某个或某些胜利粒子处于相对较优的局部最优点附近时,由于失败粒子向胜利粒子学习的机制,导致了粒子群不断向这些胜利粒子聚集,胜利粒子缺少更新,最终陷入局部最优点。根据图2所示各测试函数寻优曲线,相比较于原始CSO算法,LS-CSO算法在收敛速度上都有一定的提升,并且由于引入了基于局部搜索的二次竞争机制,部分胜利粒子处于更新了部分胜利粒子的位置和速度,防止胜利粒子集群效应引起收敛至局部最优,这使得LS-CSO算法能够更加快速寻找到全局最优值。
3 模型设计
3.1 建模流程
MWLS-SVM参数优化问题定义如下:
(14)
(15)
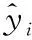
基于LS-CSO参数优化的MWLS-SVM软测量模型建模流程如下:
(1) 数据预处理:采用拉依达准则删除具有显著误差数据样本。
(2) 采用相似性准则[26]对历史运行数据进行工况分类,根据不同工况样本数量,按比例随机选取不同工况下的代表样本,再将不同工况下的代表样本按一定的比例分别划入训练集和测试集。对于任意两样本x1、x2,其相似度Sim计算如下:
Sim=e-‖x1-x2‖2
(16)
(3) 根据现场工艺流程,分析确定软测量初始辅助变量,尽可能保留与主导变量相关的特征变量,防止漏选重要特征。
(4) LS-CSO寻优算法控制参数设置:总粒子数M,最大迭代次数T,最大连续稳定代数Ts,搜索空间上下限Pupper和Plower,局部搜索范围控制因子λ。
(5) 初始化粒子群:在搜索空间上下限Pupper和Plower范围内,初始化M个粒子位置和速度,每个粒子的位置由σ、C、g确定,当前迭代次数t=0,当前稳定迭代次数ts=0。
(6) 粒子适应度计算:根据每个粒子的模型参数和训练样本,求解模型参数α和b,建立MWLS-SVM模型,对训练样本集和测试样本集进行预测输出,计算RMSEx和RMSEr获得每个粒子的适应度值。
(7) 粒子随机分组竞争:随机将粒子群两两配对,根据每对粒子的适应度,竞争决出胜利粒子和失败粒子。
(8) 粒子位置和速度更新:根据式(9)和式(10),失败粒子通过向胜利粒子学习并更新粒子位置和速度,进入下一代;在胜利粒子邻域范围内产生随机粒子,与胜利粒子进行二次竞争,竞争失败的胜利粒子进行粒子更新后和竞争成功的成功粒子进入一代,迭代次数t=t+1。
(9) 如果当前最优粒子适应度变化值小于阈值,ts=ts+1,否则ts=0。如果t (10) 根据最终优化的模型参数、最终辅助变量以及训练样本,建立软测量模型。 为了验证MWLS-SVM软测量模型性能,分别使用LS-SVM、DWLS-SVM和MWLS-SVM三种方法对燃煤电厂脱硫系统出口SO2排放浓度进行软测量建模。为了衡量上述三个模型的实际表现,通过计算模型预测最大误差(MaxError)、均方根误差(RMSE)、相对均方误差(MSRE)、校正决定系数(Adjusted R2)对模型表现进行定量描述,评价指标定义如下: (17) (18) (19) 石灰石-石膏湿法烟气脱硫(WFGD)技术以其强适应、高可靠、低成本以及高效性等优势,广泛应用于燃煤电厂尾部烟气脱硫。WFGD系统主要分为四个部分:烟气系统、吸收塔系统、氧化和浆液制备系统、石膏制备系统,整体流程如图3所示。 图3 WFGD系统流程示意图 以某燃煤发电机组WFGD系统#3吸收塔为研究对象,对2019年11月份共4 327组运行数据进行建模。初步选取了与SO2吸收相关的14个辅助变量,其中包括浆液pH值、入口SO2浓度(SO2,in)、入口烟气流量(GFin)、入口烟温(GTin)、入口氧气浓度(O2,in)、入口烟尘浓度(DCin)、出口烟气流量(GFout)、出口烟气温度(GTout)、出口氧气浓度(O2,out)、进浆液流量(SFin)、浆液密度(SD)、氧化风机A流量(OAVA)、氧化风机B流量(OAVB)和氧化风机总流量(OAV)。首先采用拉依达准则删除数据集中具有显著误差的样本,获得4 044组有效样本。根据式(10)的相似性准则,从4 044组有效样本中筛选出相似度低于0.88的729组代表样本作为训练样本,随机选取剩余样本中500组作为测试样本。 根据经过筛选的样本,分别采用LS-SVM、DWLS-SVM和MWLS-SVM方法建立脱硫系统SO2排放浓度软测量模型,模型参数均使用基于LS-CSO算法的参数优化方法进行寻优获得,寻优算法参数:总粒子数M=100,最大迭代次数T=1 000,最大连续稳定代数Ts=50,均值影响因子η=0[23],局部搜索范围控制因子λ=0.01。 根据表2中各项评价指标可以看出,三种建模方式都取得了较好的建模表现,但MWLS-SVM模型在各项评价指标上均优于LS-SVM模型和DWLS-SVM模型。MWLS-SVM模型的MaxError均低于1.2,校正决定系数在0.99以上,而LS-SVM模型和DWLS-SVM模型MaxError均在1.2以上,多数Adjusted R2低于0.99;MWLS-SVM模型的RMSE和MSRE均明显低于LS-SVM模型和DWLS-SVM模型。由此可以得出,相对于LS-SVM模型和DWLS-SVM模型,MWLS-SVM模型无论在逼近能力还是泛化能力上都有较大提高。 表2 SO2排放浓度软测量模型建模参数及评价指标统计 从图4中可知,训练样本集存在较多高局部异常因子样本,这些样本被DWLS-SVM模型识别为含有噪声的离群点,但样本离群存在三种情况[27]:一是样本存在较大噪声使其偏离了真实值;二是样本数据变量的自然变化;三是样本来源于异类。而DWLS-SVM模型降低了所有这些样本的经验权重,导致了模型弱化预测这些样本的能力,使得模型的鲁棒性降低。经过LS-CSO算法优化的建模参数如表2及图5所示,图5给出了辅助变量的特征权重,图中权重较高的七项特征分别是入口二氧化硫浓度(SO2,in)、入口烟尘浓度(DCin)、出口烟气温度(GTout)、浆液密度(SD)、氧化风机总流量(OAV)、入口烟温(GTin)和浆液pH值,文献[28]通过脱硫系统参数变动运行实验说明了上述参数对控制系统脱硫效率的影响,SO2,in和GT是对脱硫系统高效运行调节的主要依据,浆液pH、DCin和SD都是脱硫系统高效运行严格控制量,OAV是待调节量,说明了基于LS-CSO算法参数优化方法能够对模型起到优化作用。 图4 训练集局部异常因子及样本权重 图5 辅助变量特征权重图 图6和图7分别是训练集和测试集相对误差曲线,从整体上来看,MWLS-SVM模型的相对误差低于LS-SVM模型以及DWLS-SVM模型,整体表现较好。表3是训练样本和测试样本整体相对误差统计,MWLS-SVM模型中相对误差均在±5%以内,训练集95%以上样本相对误差集中在±1.2%以内,测试集95%以上样本相对误差集中在±2.5%以内,各项统计值均优于LS-SVM和DWLS-SVM模型。因此,仿真结果表明MWLS-SVM模型能够对脱硫系统进行准确的描述,具有更好的逼近能力和泛化能力。 图6 各训练样本相对误差〗 图7 各测试样本相对误差 表3 SO2排放浓度软测量相对误差统计 续表3 本文针对最小二乘支持向量机软测量建模过程中存在的噪声和辅助变量差异性对模型的影响问题,在直接加权最小二乘支持向量机基础上提出了一种混合加权最小二乘支持向量机的建模方式,同时将局部搜索算法应用于竞争粒子群胜利粒子更新,提高了算法全局搜索能力、搜索速度和精度,最终建立了一套基于LS-CSO优化MWLS-SVM的软测量建模方法。本文根据脱硫系统工艺流程分析以及实际历史运行数据,选取辅助变量,采用LS-CSO对模型参数和特征权重进行优化,最终建立脱硫系统出口SO2软测量模型,同时与DWLS-SVM模型和LS-SVM模型进行了模型性能比较,预测结果说明MWLS-SVM模型在逼近能力、泛化能力以及预测精度上均有较大提升,模型相对误差控制在5%以内。因此,本文提出的基于局部搜索竞争粒子群优化的MWLS-SVM模型是一种有效的软测量建模方法。3.2 模型评价指标
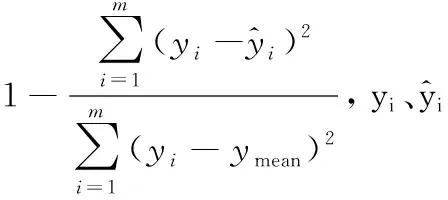
3.3 石灰石-石膏湿法烟气脱硫软测量建模


4 结 语

