分散式农村污水基于三维荧光光谱和紫外-可见全波段吸收光谱的“聚类-回归”COD预测模型

周铭睿，曲江北，李 彭*，何义亮

1. 上海交通大学中英国际低碳学院，上海 201306 2. 上海交通大学环境科学与工程学院，上海 200240

引 言

近年来，随着国家对环境保护政策的相继提出以及人民的环境保护意识的不断提高，水环境保护问题愈来愈成为人们关注的对象，水环境中的水质在线监测也越来越成为关注的焦点。 在环境大数据，环境智能化的趋势下，在线监测设备需要有成本低、 监测实时连续、 易维护、 无污染等特点。 无论是城市还是农村，污水中溶解性有机物含量一直是一项重点控制的指标[1]。 化学需氧量(COD)作为一种表征污水中有机物含量总体水平的重要指标，有检测精度很高的传统化学法，但传统化学法的检测时间长、 维护成本高、 所采用的化学试剂具有二次污染等不足之处[2]，无法满足在线监测的需求，且难以大量布设，无法获得实时的数据。 尤其是对于农村污水，其采用分散式处理的模式，污水处理设施规模小、 设置位置分散、 数量多[3]。 所以需要寻求一种快速、 精确、 高效的实时在线监测方法及模式来满足水质的在线监测。

目前，光谱法应用于水质COD的在线监测已具有很多鲜明的优势。 与传统化学法相比，光谱法，尤其是紫外-可见光谱法在监测COD方面具有操作简单、 检测速度较快、 无二次污染、 可实现实时连续测量等优势[4]，使得紫外-可见光谱法在COD的监测领域得到了广泛研究。 但是，对于组分复杂且种类不同的污水来说，仅仅使用紫外-可见光谱法来预测水质中的COD，其预测精确度和稳定性仍待提高。 现有的研究多采用实验室配水来进行光谱法模型的校准和预测，配水多为固定的有机物组成，但实际水体中的有机物成分复杂且不固定，所以许多研究缺乏不同有机物组成样本的研究，导致使用光谱法在不同水体环境中应用时存在监测精度较低，难于推广应用的问题。 而三维荧光光谱法(excitation-emission matrix, EEM)用来描绘荧光有机物的荧光信息，具有数据量大且完整等特点[5]。 三维荧光光谱的荧光数据解析得到激发光谱矩阵、 发射光谱矩阵以及得分矩阵，其中得分矩阵在一定条件下正比于荧光物质浓度，可进行半定量表征[6]。 且不同类型的有机物在三维荧光光谱上的峰位置有显著差异，因此可以利用不同水样的三维荧光光谱，按照有机物组成的近似度划分类别。 三维荧光体积积分法对特定的荧光区域进行标准体积积分可以间接表示不同组分的相对浓度[7-8]。 高连敬等[9]以三维荧光光谱技术为手段，结合荧光区域积分(FRI)方法，证明其可以有效监测和分析水体中低浓度有机物的去除情况，可以作为一种有效的技术手段，用于净水厂的日常运行和水质监测。 孔德明[10]等利用平行因子分析(PARAFAC)方法分解去散射后的三维荧光光谱后的数据，实现了对污染物的快速、 有效的检测。 但是，目前没有公认的用于三维荧光光谱数据特征分析处理的方法，也没有将污水水样分类再建立预测模型的尝试。 我们的研究尝试将这两种方法进行对比，观察对COD预测效果的影响。

以实际生活污水为研究对象，对水样的三维荧光光谱分别使用荧光体积积分(FRI)算法、 平行因子分析(PARAFAC)算法，提取水样的荧光特征信息再使用FCM算法进行水样的聚类。 对聚类后不同类别水样的紫外-可见全波段光谱和COD数据进行偏最小二乘法(PLS)模型的回归及预测，从而建立一种全新的“聚类-回归”COD预测模型，具体过程如图1所示。

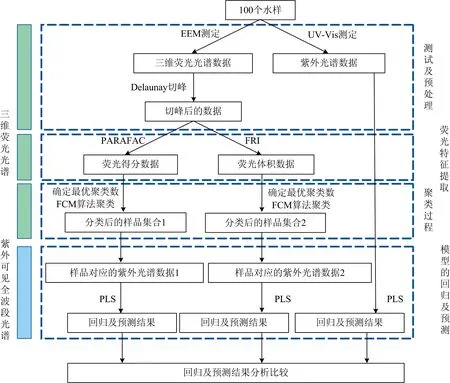
图1 模型设计流程图Fig.1 Flow chart of model design

1 实验部分

1.1 样本采集与光谱检测

水样采集地点为江苏省常熟市，采集地点为常熟市周边的农村区域，采集时间为2019年3月10日。 为满足样品有机物组成的多样性，采集时选取100个分散式农村生活污水处理装置出水作为采集点，每个采集点采1个水样，具体的采集信息见图2。 采集后的水样使用250 mL聚乙烯瓶在4 ℃低温条件下贮存，样品的COD浓度使用国标法测定。

水样的紫外可见光谱数据由HACH DR/6000光谱仪扫描得到，扫描范围为200～1 000 nm，间隔为1 nm。 水样的三维荧光光谱数据由日立F-7000荧光分光光度计扫描得到，激发波长的扫描范围为200～500 nm，间隔为5 nm； 发射波长的扫描范围为250～550 nm，间隔为5 nm。 为了避免仪器本身的散射对三维荧光光谱测试的影响，设置初始的发射波长滞后于初始的激发波长50 nm。

1.2 数据处理

1.2.1 平行因子分析算法(PARAFAC)

平行因子分析(PARAFAC)方法是一种基于三线性模型

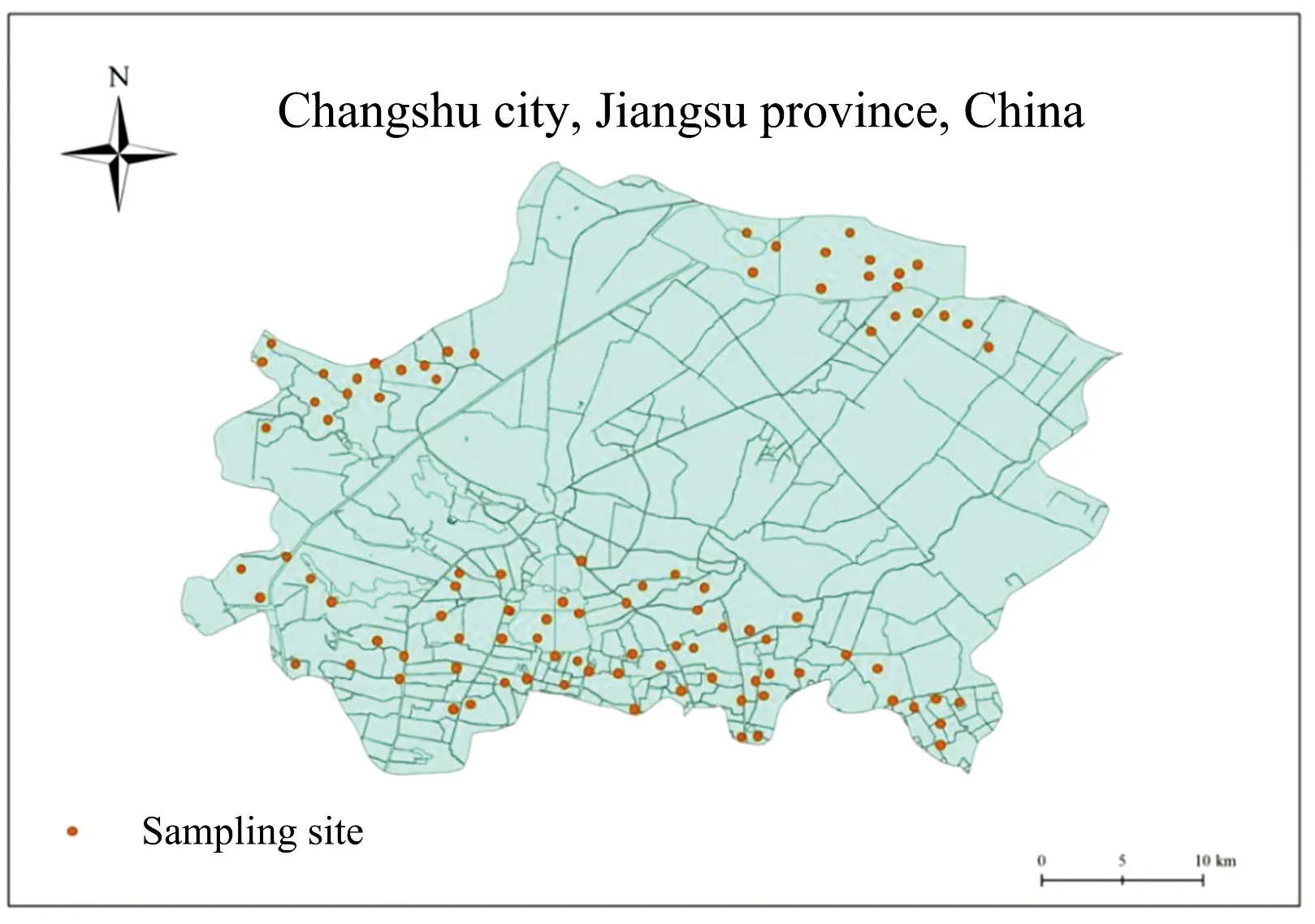
图2 常熟市采样分布图Fig.2 The map of sampling sites in Changshu

实现多维数据矩阵分解的经典迭代算法。 传统的三维荧光光谱数据通常采用寻峰法进行特征荧光团的识别，但对于多组分水样通常会有峰重叠的现象，造成荧光峰被全部或部分掩盖的情况，导致检测结果误差偏大[11]。 使用平行因子分析(PARAFAC)方法首先需要建立一个三维矩阵X，矩阵类型为I×J×K。 其中I和J分别是三维荧光光谱的激发波长和发射波长的扫描个数。 三线性模型分解过程可以表示为

(1)

式(1)中，i=1, 2, …,I;j=1, 2, …,J;k=1, 2, …,K;xijk为三维荧光光谱矩阵X中的元素；aim为相对激发光谱矩阵中的任一元素；bim为相对发射光谱矩阵中的任一元素；cim为相对浓度矩阵中的任一元素；eijk为残差矩阵中的任一元素；M为得分矩阵、 负荷矩阵的列数。

1.2.2 荧光体积积分算法(FRI)

将三维荧光光谱的等高线图分为5个连续的区域Ⅰ，Ⅱ，Ⅲ，Ⅳ和Ⅴ。 王聪颖等在研究中指出，荧光光谱的特定区域可以间接反映水体中部分可溶性有机物，区域Ⅰ(Ex<250 nm, Em<330 nm)，区域Ⅱ(Ex<250 nm, 330 nm250 nm, Em<380 nm)，区域Ⅴ(Ex>250 nm,

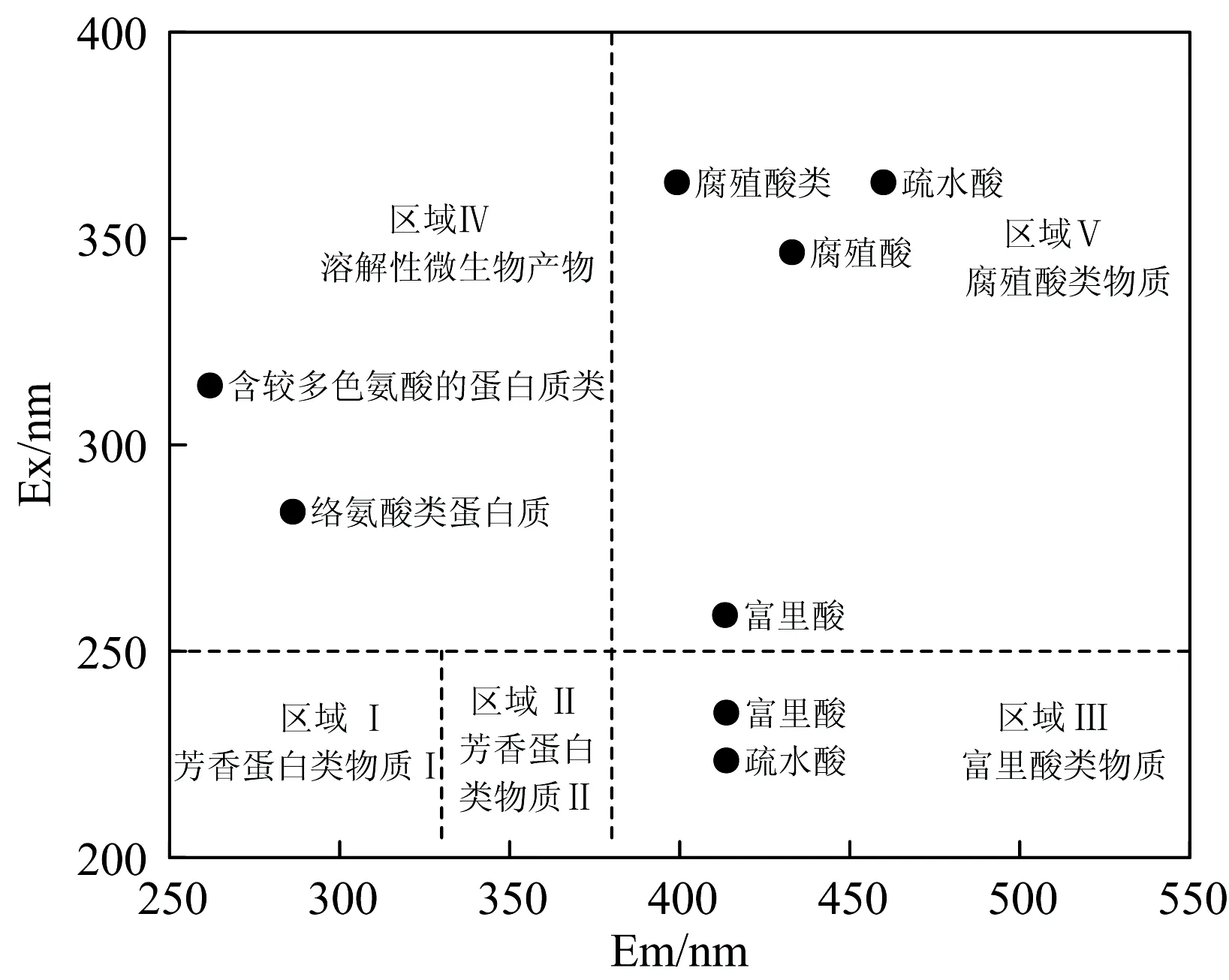
图3 三维荧光物质区域分布Fig.3 Three-dimensional map of the regionaldistribution of fluorescent substances

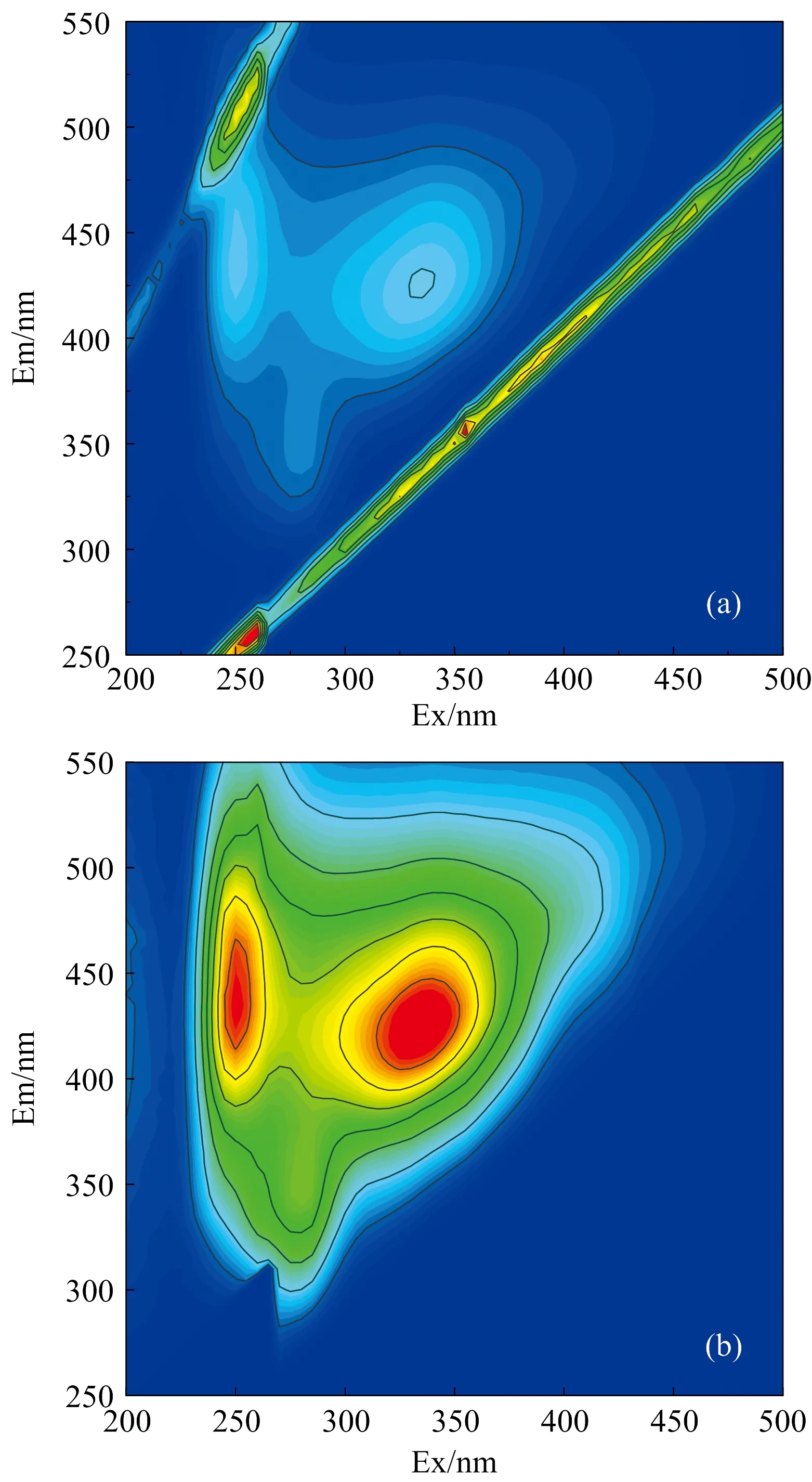
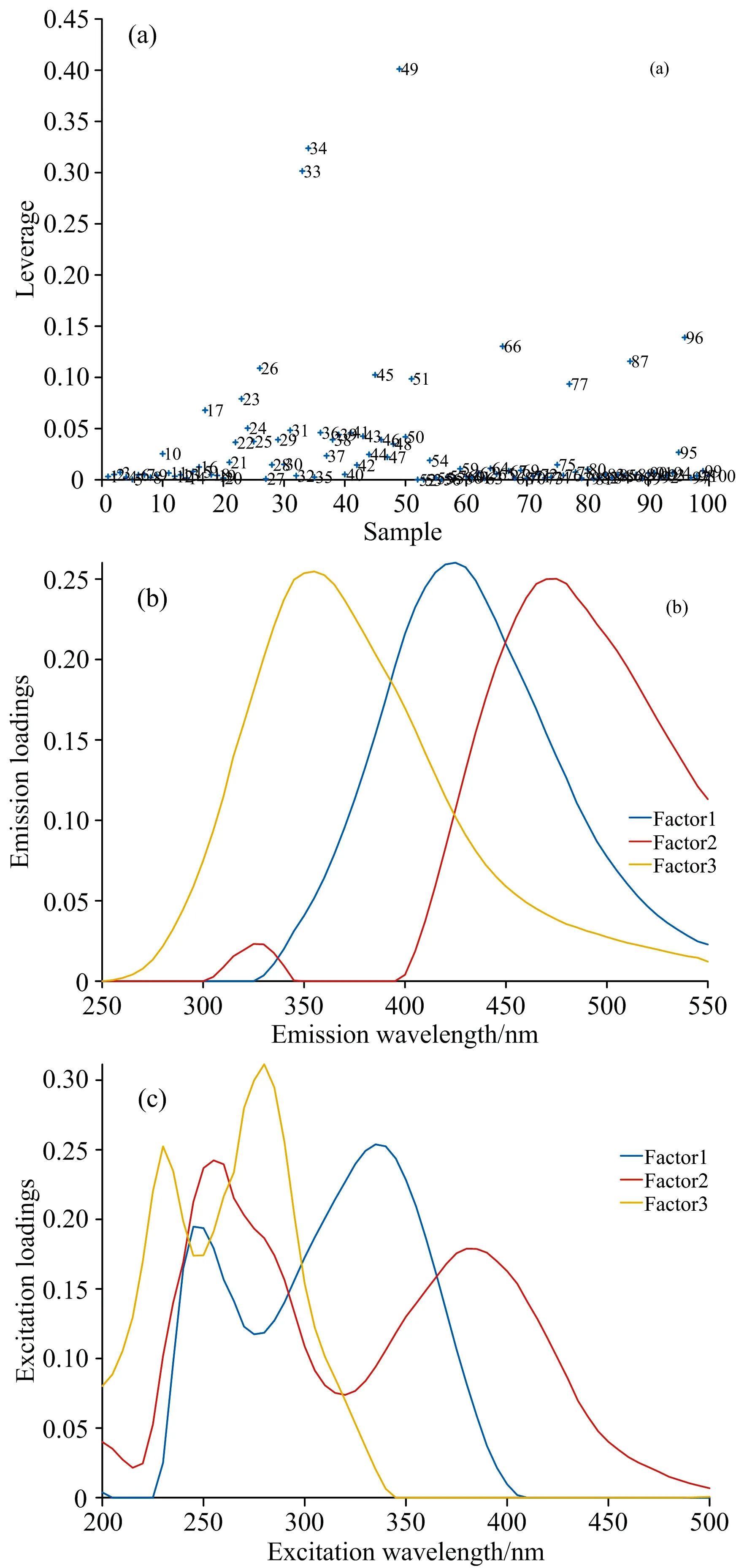
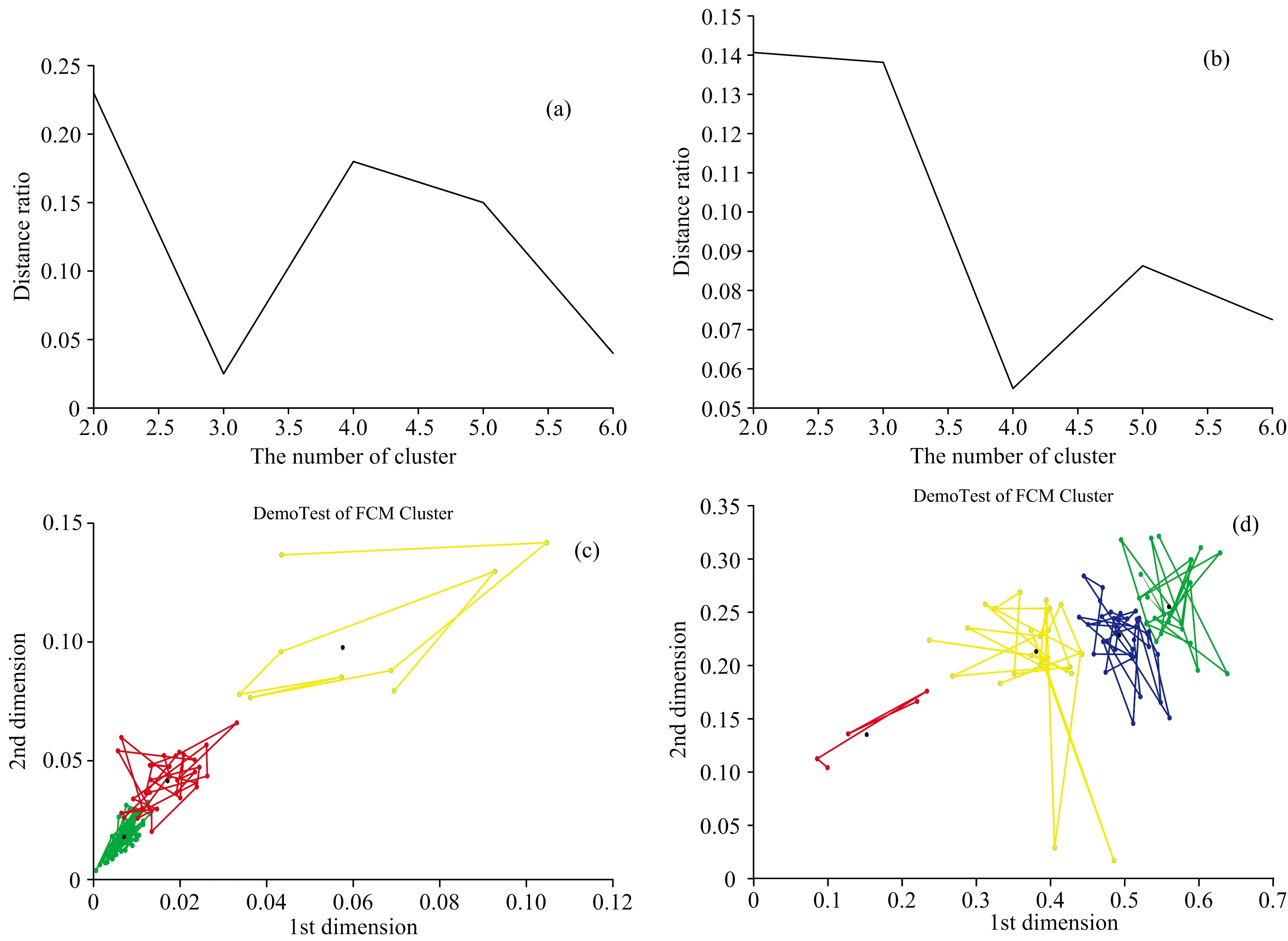
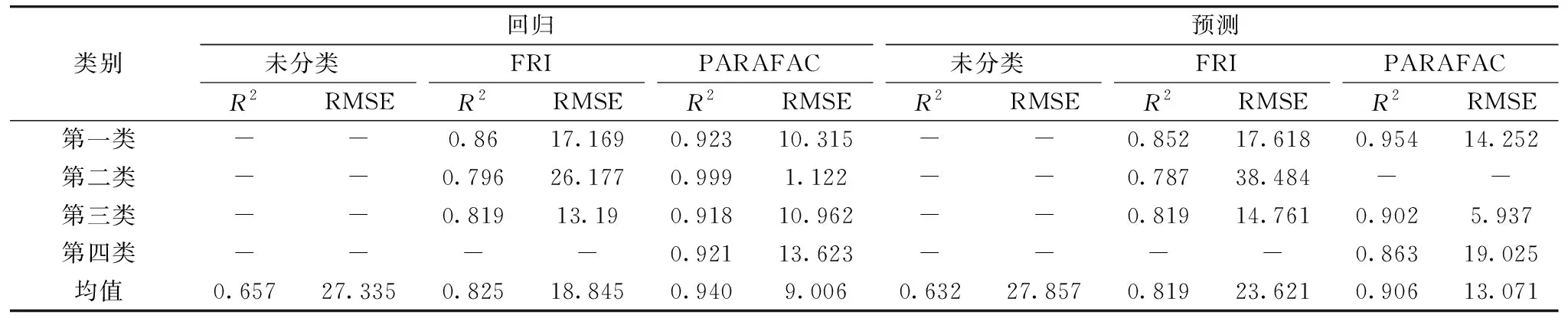
380 nm

(2)

式(2)中，i=1, 2, …, 5；φi是区域i的区域积分和；E(λExλEm)为三维荧光光谱在激发波长λEx和发射波长λEm处的强度值； ΔdλExΔdλEm分别为激发波长λEx和发射波长λEm的积分增量。

1.2.3 最优聚类数与FCM算法

聚类通常是指运用特定标准(如距离标准)将数据集分割成为不同的类或者簇，使得簇内的数据相似度尽可能高，簇间的数据相似度尽可能小，最终使得特征高度相似的数据相聚成簇。 聚类与分类不同，聚类是一种无监督学习模式，即不需要给定特定的数据划分特征，在聚类过程中即可自聚类成簇。 对于成分复杂的水样来说，其特征是不明确的，因此使用聚类方法可以对不同特征的样品进行区分。

最优聚类数的确定也是依据距离标准，通过簇内离差矩阵来描述数据的紧密度，通过簇间离差矩阵来描述数据的分离度。 簇内簇间离差度比值指标D的定义为

(3)

式(3)中，n表示聚类的数目；i表示当前所运算的类； trA(i)表示簇内离差矩阵的迹； trB(i)表示簇间离差矩阵的迹。

FCM算法又称模糊C-均值聚类算法，是基于目标函数最优的聚类算法。 通过隶属度函数来确定数据间的相似度，算法的目标函数和约束条件可以描述为

(4)

(5)

式中，m为聚类数目，即最佳聚类数；n为数据总数；uij为每个样本j属于某一类i的隶属度。

2 结果与讨论

2.1 光谱预处理

对荧光光谱影响较大的拉曼散射和瑞利散射在使用光谱仪对水样进行测定时无法被直接去除，两种散射的存在可能会导致使用荧光体积积分(FRI)算法和平行因子分析(PARAFAC)算法进行分析时有效光谱信息被掩盖，导致分析结果产生严重偏差，所以在进行光谱信息分析前需要去除散射的干扰。 分析图4(a)和(b)： 通过MATLAB R2018b，使用Delaunay三角形内插值方法可以有效去除两种散射对荧光光谱的影响，使本身的荧光信息更加明显。

2.2 基于荧光体积积分和平行因子分析算法

采用荧光体积积分(FRI)算法对预处理后得到的三维荧光矩阵X进行分析，矩阵X结构为100×61×61(100为样品数量，61为激发波长数量，61为发射波长数量)。 荧光积分区域依据可被荧光所反映的水体中的溶解性有机物质分为5个区域，分别为芳香蛋白类物质Ⅰ区域、 芳香蛋白类物质Ⅱ区域、 富里酸类物质区域、 溶解性微生物代谢产物区域、 腐殖酸类区域。 所以由荧光体积积分(FRI)算法得到的荧光特征信息矩阵为二维矩阵X1(100×5)。 但是使用荧光体积积分(FRI)算法就默认了每个水样均有5个荧光特征区域，且重叠的荧光信息无法分开，可能会造成提取的荧光特征信息出现部分冗余，对之后的聚类过程造成一定的影响。

图4 水样的荧光光谱图(a)： 去除散射前的三维荧光光谱； (b)： 去除散射后的三维荧光光谱Fig.4 Fluorescence spectra of water samples(a)： Three-dimensional fluorescence spectra before removal of scattering;(b) Three-dimensional fluorescence spectra after scattering removal

采用平行因子分析(PARAFAC)算法对预处理后得到的三维荧光矩阵X进行分析，对100个样本进行荧光数据的杠杆验证时发现33，34和49号样品的验证杠杆值明显偏离其他样品，结果如图5(a)所示，应当剔除此三种样品。 对剔除异常样品的97组数据进行平行因子分析，利用对半分析验证不同组分情况下的模型稳定性，分别验证了2～7组分下模型的稳定性，由计算结果得出只有3组分情况下模型是稳定的。 所以由平行因子分析(PARAFAC)算法得到的荧光特征信息矩阵为二维矩阵X2(97×3)。 由图4(b)和(c)可知三个特征荧光峰的位置： 第一个特征荧光峰激发/发射波长为335/420 nm; 第二个特征荧光峰激发/发射波长为255/470 nm； 第三个特征荧光峰激发/发射波长为280/350 nm。 使用平行因子(PARAFAC)算法对三维荧光矩阵进行处理时，可以去除与其他水样荧光信息有明显差异的异常水样，并应用对半分析方法模型对选取的特征组分数进行稳定性的验证，保证了选取的特征组分数为最优组分数，使荧光信息的特征更加的明显。 此外，平行因子分析(PARAFAC)算法还能将重叠的荧光特征峰进行数据层面的分离，保证了特征信息不出现冗余的情况，使之后的聚类效果更优。

图5 水样的平行因子分析(a)： 样品的杠杆分析； (b)： 组分数为3的发射波长对半分析；(c)： 组分数为3的激发波长对半分析Fig.5 PARAFAC of water samples

2.3 基于模糊c-均值聚类算法的聚类结果分析

为了更好地将水样依据FRI算法和PARAFAC算法提取出来的荧光特征信息进行聚类。 首先应该选取最优聚类数，利用基于距离指标的最优聚类数选取方法，分别对使用了FRI算法和PARAFAC算法进行荧光特征提取的水样进行最优聚类数选取。 如图6(a)可知，使用FRI算法提取荧光特征的水样的最优聚类数为3。 如图6(b)可知，使用PARAFAC算法提取荧光特征的水样的最优聚类数为4。

其次在MATLAB R2018b中使用FCM算法分别对FRI算法和PARAFAC算法分析得到的荧光特征数据进行3类别和4类别的聚类，聚类结果由图6(c)和(d)所示。 其中，将FRI算法得到的荧光特征数据分为3类： 第一类57个样品、 第二类34个样品、 第三类9个样品，总共100个样品。 将PARAFAC算法得到的荧光特征数据分为4类： 第一类36个样品、 第二类5个样品、 第三类29个样品、 第四类27个样品，总共97个样品。 具体的分类结果由表1所示，由表1中的结果可知，两种方法提取出的荧光特征数据主要特征较为相似，所以每一类的样品重合率均较高。 但使用FRI算法提取特征信息再聚类后，每一类的样品在重复的样品之外出现了不少冗余样品，可能是FRI算法在处理荧光光谱数据时未剔除与特征荧光峰重叠的干扰信息造成的。

表1 具体的聚类结果Table 1 Specific clustering results

图6 FCM聚类分析结果(a)： 使用FRI后的最优聚类数选择； (b)： 使用PARAFAC后的最优聚类数选择；(c)： 使用FRI后的聚类结果； (d)： 使用PARAFAC后的聚类结果Fig.6 FCM cluster analysis results(a)： Selection of the optimal cluster number after using FRI; (b)： Selection of the optimal cluster number after using PARAFAC;(c)： Clustering results after using FRI; (d)： Clustering results after using PARAFAC

2.4 聚类后的模型拟合及预测

利用The Unscrambler X软件中的偏最小二乘法(PLS)对聚类后的各类水样的紫外-可见全波段光谱与对应的COD数据进行模型的回归及预测，回归及预测结果如表2所示。 其中决定系数R2表示因变量的变异部分可由自变量的变异来解释，R2越接近1，模型的参考价值越高； 均方根误差RMSE指预测值与真实值的偏离程度，RMSE越小，模型的参考价值越高[12]。 由表2结果可知，无论是运用FRI算法还是PARAFAC算法提取的荧光特征数据聚类后再建立紫外-可见全波段光谱和对应的COD数据之间的偏最小二乘(PLS)模型回归结果均优于未分类的结果，说明对水样进行聚类后再建模能有效提高模型的精度与稳定性； 且由表2可知，由平行因子分析(PARAFAC)算法提取的荧光特征数据进行聚类后再建立紫外-可见全波段光谱和对应的COD数据之间的偏最小二乘(PLS)预测模型的COD预测精度高于由荧光体积积分(FRI)算法提取的荧光特征数据进行聚类后再建立紫外-可见全波段光谱和对应的COD数据之间的偏最小二乘(PLS)预测模型的COD预测精度，说明平行因子分析(PARAFAC)算法提取出的荧光特征数据的特征性优于由荧光体积积分(FRI)算法提取出的荧光特征数据； 由平行因子分析(PARAFAC)算法聚类后的每一类类内的水样特征相似度高于由荧光体积积分(FRI)算法聚类后的每一类类内的水样特征相似度。 可能是平行因子分析(PARAFAC)算法将与荧光特征峰重叠的无效荧光信息分开，而荧光体积积分(FRI)算法直接进行荧光的积分，未考虑重叠的无效荧光信息的影响，使得使用荧光体积积分(FRI)算法提取的荧光特征数据存在信息冗余。 使用平行因子分析(PARAFAC)算法结合FCM聚类后的聚类效果优于使用荧光体积积分(FRI)算法结合FCM聚类后的聚类效果，类内水样的相似度更高，使得预测精度更高。

表2 模型的回归及预测结果Table 2 The model fitting and prediction results

3 结 论

利用三维荧光光谱结合平行因子分析(PARAFAC)算法和FCM聚类算法对聚类后的水样的紫外-可见全波段光谱和相应的COD数据运用偏最小二乘(PLS)模型进行回归和预测。 研究结果表明，使用Delaunay三角形内插值法去除拉曼和瑞利散射后，使用平行因子分析(PARAFAC)算法提取荧光特征信息并使用FCM算法聚类，使用聚类后各类水样的紫外-可见全波段光谱数据和相应COD数据进行偏最小二乘(PLS)模型的回归和预测，具有最佳的拟合和预测结果，回归平均R2为0.940，平均RMSE为9.006，预测平均R2为0.906，平均RMSE为13.071，相比于未分类的PLS模型预测平均R2值0.632，R2提高了0.274。 本研究提供了一种使用三维荧光光谱数据，利用平行因子分析(PARAFAC)算法提取荧光特征的先聚类再建模的方法，可为水样的快速检测提供一种新思路。 但是，此方法由于需要测量样品的三维荧光光谱数据和紫外-可见全波段光谱数据，在实时在线监测的设备化方面仍需改进，后续可以进一步研究，以提高此方法的实际应用性。