带时间窗的低碳车辆配送路径优化研究

文/王浩青 郑金诺

针对当前环境问题日益严峻，低碳车辆配送路径优化在减少碳排放方面有着重要意义。在以往的车辆配送路径问题中只考虑经济成本最小而忽略了碳排放。本文首先将碳排放转化为碳排放成本，构建了总成本最小的目标优化模型，其次采用蚁群算法对优化模型进行求解，最后通过算例验证了模型的有效性，为减少车辆碳排放提供参考和决策支持。

0.引言。

近年来，物流活动成为了我社会经济发展的必要条件，随着配送需求不断增加，配送车辆数量也随之增加，势必会产生更多的碳排放，实现低碳车辆配送路径是解决环境的关键。优化车辆行驶路线，即求解车辆路径问题（Vechicle Routing Problem，VRP），1959年由Dantzi和RamserP[1]首次提出，是0-1整数规划的NP-Hard问题。Solomom[2]等首次引入时间窗概念，即（Time Windows VRP）TWVRP。Jabali[3]等提出了软时间窗的VRP问题模型。低碳车辆路径问题（Low-carbon Vehicle Routing Problem,LCVRP）是基于传统车辆路径问题（VRP）的研究基础，加入了碳排放的约束。已有不少文献研究了碳排放因素对物流运输业的影响，当市场中存在碳交易机制时，物流配送路径问题便需要考虑碳排放带来的成本。在减少车辆碳排放方面，吴丽荣[4]等建立了车辆燃料消耗的模型并进行求解。康凯[5]等人在模糊约定时间窗车辆路径优化问题研究中考虑了碳排放因素并转化为碳排放成本。代楚楚和徐菱[6]建立了基于时间依赖车辆路径问题模型的快递企业低碳配送车辆路径选择模型，并设计了多种群遗传算法对模型进行求解。王钰青[7]等将车辆行驶路程、运输途中载货量和碳排放量进行综合考虑，建立基于最小碳排放量的广义旅行商模型来寻求最优配送路径。本文从上述问题入手，研究考虑碳排放因素的带时间窗车辆物流配送路径优化问题，引入碳排放成本机制，构建以总成本为目标的数学模型，同时采用蚁群算法进行求解出最优路径方案。

1.问题描述。

一个配送中心为多个客户点提供配送服务，客户点的坐标、时间窗、需求量已知，目标是求解出总成本最小化的最优路径方案。为了界定研究范围，作出如下假设：（1）车辆为同质车辆，车辆完成任务后返回配送中心（2）各个客户点均有时间窗要求，不能提前或者延后服务（3）客户需求量小于车辆最大装载量（4）车辆配送过程中速度保持恒定，不受道路情况影响（5）车辆在客户点服务时，不会产生碳排放。

2.模型构建

2.1 符号定义

为配送客户点的集合，u∈U；U0为配送中心和客户点构成的集合，U0=U∪{0}，0表示配送中心；A为节点之间弧的集合，A={（i，j），i≠j，i∈N，j∈N}；K为配送车辆k的集合，k∈K；qt为客户点q的需求，且maxqt≤Q，i∈U；[ei，li]为客户点i的服务时间窗；dij为客户点i和客户j之间的距离；r为每使用一辆车的租赁成本；v为车辆行驶速度；γ为二氧化碳排放系数；s为碳排放成本。

Xik为0-1变量，当节点i由车辆k服务时值为1，否则为0；Xik为0-1变量，当弧（i，j）上有车辆行驶时值为1，否则为0。yik为0-1变量，当车辆在弧（i，j）上行驶时值为1，否则为0。

2.2 碳排放计算公式。由于Barth的综合油耗模型考虑到车辆载重、速度和行驶距离对车辆油耗的影响，能够给出任意载重和速度组合下车辆匀速行驶时的综合油耗，所以本文采用其油耗模型，并引入碳排放系数γ，以此将油耗量转换为碳排放量，N表示发动机转速，V表示机排量，v表示车辆速度，d表示行驶距离，μ代表车辆自重，f表示车辆的装载量，ξ表示燃料与空气质量比，A表示车辆正面表面积，κ表示常量，ηtf表示车辆转动效率，θ表示道路角度，g表示引力常数，Cd表示空气阻力系数，Cr表示滚动阻力系数，ρ表示空气密度，λ=ξ/κψ，γ=1/（1000ηtfη），α=τgsinθ+gCrcosθ，β=0.5CdAρ，化简后如式（1）所示，F=λ（kNV+γβv3+γα（μ+f）v）d/v=λ

式（1）可以分为三个部分，第一部分kNV/v可以认为是发动机模块的油耗，为与行驶时间呈正比例关系的线性函数，第二部分γβdv2可以被认为是速度模块的油耗，为速度的二次函数，第三个部分γα（μ+f）d为重量模块的油耗，独立于速度和行驶时间，与车重和行驶距离直接相关。

2.3 数学模型

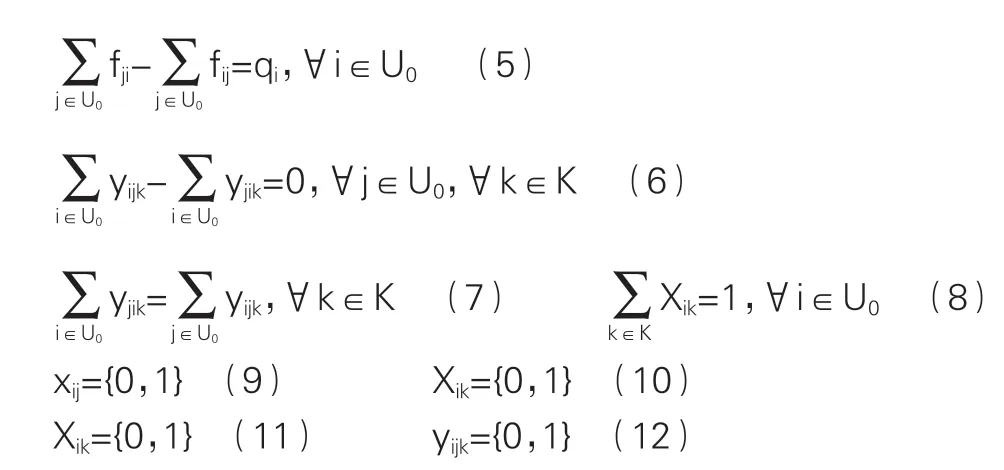
式（3）表示每辆车只使用一次；式（4)表示流量守恒；式（5）表示每个客户需求得到满足；式（6）表示车辆服务完客户点离开；式（7）表示车辆到达和离开是同一客户点；式（8）表示每个客户只被服务一次；式（9）-（11）表示决策变量。

3.蚁群算法求解。

蚁群算法是蚂蚁之间是相互帮助，如果蚂蚁在一条没有走过的路上行走时，会随机选择一条路，在此路程中会留下信息素，路径越长，留下的信息素浓度会越少，相反，信息素的浓度就会越多，后面行走的蚂蚁通过自身感知信息素浓度的高低来决定走哪条路，信息素浓度越高，蚂蚁选择这条路的概率就会越大。经过长时间后，蚂蚁通过传递自身的信息素从而形成一种正反馈机制。最终，所有的蚂蚁会找到一条距离最短的路径也就是最优路径。蚁群算法具有较强的鲁棒性[8]，因为蚁群算法的参数较少，对初始解的依赖性低，对它的基本模型进行简单修改便可以应用到其他众多领域。因此在车辆配送中，车辆对初始路线选择的随机性较高，基于蚁群算法这一特性，在对车辆行驶路线搜索过程中不断调整，从而获取最优路径。本文研究的配送车辆路径规划中，每个车辆代表蚂蚁，各个客户点与配送中心之间的相互距离表示行走的路线。基于上面所述的原理将车辆的行驶路线形成一个正反馈机制，在本文设计配送路线中，形成一个满足约束条件的最短路径，从而降低车辆产生的碳排放。蚁群算法在解决带时间窗的车辆配送问题时，算法步骤如下：Step 1初始化蚁群算法各个参数，设置蚁群数量m，t时刻时弧（i，j）的信息素浓度为τij；Step 2每只蚂蚁从配送中心出发，爬行路径由信息素浓度确定，将所有在客户点的蚂蚁下一个访问的客户点集合存储到禁忌表中；Step 3蚁群重复以下步骤，最后将所有客户点遍历一遍；Step 3.1通过转移概率计算公式，蚂蚁将选择下一个客户点。具体为蚂蚁根据每条弧上的信息素浓度选择下一个客户点，假设蚂蚁在时刻从客户点i出发，选择客户点j的状态转移概率表达式为式（12）：

τij（t）表示客户点i和客户点j之间的信息量浓度，α表示信息素浓度，β为期望启发因子，Ak表示车辆k可以被允许选择的客户点，ηij表示客户点j对于客户点i的启发程度。Step 3.2如果客户点i满足约束条件，则蚂蚁m转移到客户点；

Step 3.3将符合约束条件的客户点加入到禁忌表中；

Step 4更新全局信息素。信息素浓度更新表达式为式（13）：

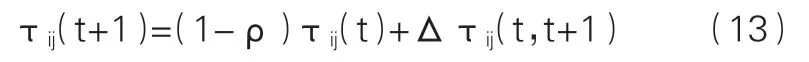
△τij（t，t+1）表示在（t，t+1）时间段内，弧上（i，j）的信息素增加量，ρ表示信息素挥发系数；

Step 5每次迭代Nc=Nc+1，如果Nc=Ncmax，则返回到Step2；否则就输出最优解并结束算法。

4.算例分析。

为了验证本文提出的模型有效性，现采用Solomon的VRP数据集中的算例C101对模型算法进行检验。选取数据集中1个配送中心和25个客户点，蚁群算法参数设置为：m=100，Ncmax=100，α=1，β=3，ρ=0.8，车辆参数设定如下：r租赁成本=100，ξ空气与燃料质量比=1，κ标准柴油燃料的热值(kg/g)=44，ψ从克g/s到升l/s的换算系数=737，k发动机摩擦系数（kj/rev/l）=0.2，N发动机转速（rev/s）=33，V发动机排量（l）=5，ρ空气密度（kg/m3）=1.2，A迎风表面积m2=3.19，μ车辆自身重量（kg）=6300，g引力常数=9.8，θ道路角度=0，Cd气动阻力系数=0.7，Cr滚动阻力系数=0.01，ε车辆传动系效率=0.4，ω燃 油 机 效 率 参 数=0.45，γ碳 排 放 系 数=2.61（kg/l），s碳排放成本=20（kg/元），v车辆行驶速度=50（km/h）。在CPU为2.9GHz，内存为8GB，使用MATLAB2020a计算机上编程计算得到以下优化方案：当不考虑碳排放，以运输成本最小为目标函数时，车辆总使用数为4辆，车辆总行驶距离为182.3257，租赁成本为400，碳排放量为403.2565；优化后，车辆总使用数为3辆车，车辆总行驶距离191.8136，最低碳排放量为400.3714，租赁成本为300，碳排放成本为8007.428，1号车辆配送路线为0→5→3→7→8→10→11→9→6→4→2→1→0，2号车辆配送路线为0→13→17→18→19→15→16→14→12→0，3号车辆配送路线为0→20→24→25→23→22→21→0。相比于优化前，虽然车辆总行驶距离增加了，但碳排放量减少了0.71%。以上结果仅仅是对于25个客户点来进行计算求解，如果对于实际生活，减少的碳排量会更多。

5.结论

本文综合考虑包含配送车辆租赁成本和碳排放成本，建立了考虑时间窗的低碳车辆配送路径优化数学模型，采用蚁群算法求解所提模型，并通过具体算例对本文的模型和算法进行仿真，与不考虑碳排放的车辆配送路径方案对比，可以得到优化后的路径方案，这对于我国物流企业实施低碳物流有很大的促进作用。因此本文所建模型和求解算法对于带时间窗的低碳车辆配送路径规划具有适用性和有效性，对低碳物流的发展提供了有效的支持。