交通限行背景下多目标城市配送路径优化研究

文/田爱玄

交通限行政策虽然缓解了城市交通压力和环境污染，但也增加了城市配送的作业难度。本文针对交通限行背景，建立以配送成本、客户满意度、碳排放成本为多目标的城市配送路径优化模型。最后进行算例分析，验证模型的有效性及适用性。

一、引言

城市配送作为物流链条的最后一公里，在城市生产制造、消费经济等方面的基础保障作用日益突出。尤其在电商飞速发展时代，城市配送高频次、多品种、小批量的需求日益增长，其造成的道路资源紧张、环境污染等环境负外部性也逐渐凸显。为缓解这一现状，各城市相继推出限行政策，但这无疑会降低城市配送效率。在此背景下，如何针对交通限行背景下，合理安排配送路线显得尤为重要。随着限行政策的逐步实施，学者们将实际交通状况考虑进城市配送路径优化问题中。刘建仁[1]针对交通拥堵问题，基于蚁群算法构建以降低成本为目标的城市配送路径优化方案。赖平仲等[2]以交通限行政策及客户软时间窗为基础，构建了以配送成本最低为目标的车辆路径优化模型。胡云超等[3]对城市配送主体进行博弈分析，建立了考虑交通限行的多目标路径优化模型。戢晓峰等[4]基于不同交通管制时间窗对城市物流配送优化的综合效益进行对比。肖建华等[5]等以碳排放及运输成本最小化为目标，构建多能源多车型的车辆路径优化模型。由此可见，目前针对交通限行政策的城市配送路径优化研究多从配送企业出发，以配送成本最低、配送时间最少或配送路径最短为优化目标。但实际中，城市配送所涉及的利益相关主体还包括城市配送客户和社会环境两大主体。物流降本增效的迫切性、客户配送时间窗的多样化、运作过程的低碳化均对城市配送提出了更高的要求。因此，本文以交通限行为背景，综合考虑城市配送相关利益主体，衡量配送成本、客户满意度及碳排放成本等城市配送发展目标，构建城市配送的最优路径模型。

二、基于熵权法的城市配送路径优化多目标权重分析

本文以配送企业的配送成本、配送客户的服务满意度及社会环境的碳排放成本为优化目标，并基于专家打分法和熵权法分析多目标间的权重关系∶

则配送成本、客户满意度、碳排放成本等城市配送路径优化多目标权重矩阵为（0.4545，0.3750，01705）。

三、数学模型

本文研究的城市配送路径优化问题为单一配送中心到多客户点的配送问题，且配送客户具有软时间窗限制，客户最满意的配送时间为[TAi，TBi]，最大容忍的配送时间为[TCi，TDi]（[TAi，TBi]■[TCi，TDi]）。同时车辆严格遵守城市的限行政策，不可违背通行时间[TEi，TFi]限制。

（一）符号设置

根据城市配送问题特征作出假设：配送中心位置已知，货物容量无限制；客户位置及货物需求量已知，且货物可混装，每个客户仅能被一种车型中的某一辆车服务一次；配送中心车辆为多车型，车型数确定且车辆数量可满足配送需求；由于交通限行政策的施行，本文认为城市交通拥堵状况有所改善，因此车辆在配送过程中能保持匀速行驶；当车辆到达客户的时间早于客户可接受的最早配送时间时，会产生等待成本，当到达时间晚于客户可接受的最晚配送时间时，会因迟到而产生惩罚成本，假设所有车型车辆所产生的等待成本和惩罚成本相同。为方便叙述，对下列参数进行说明：设无向图G=（N，M）中，N={N0，N1，…，Nn}是所有点的集合，N0表示配送中心，为配送点个数。M={Mij，i≠j，ij}表示所有路径的集合。符号设置包括：C'为城市配送企业配送费用；V为城市配送客户满意度带来的总体潜在价值；C''为城市配送过程中产生的碳排放成本；Vi为客户i的满意度；Q为配送车辆的车型数；q为配送车所使用的车型；Kq为配送中心每种车型的车辆数；Wq为每种车型的车辆载重量；Kq为使用第q中车型中的车辆进行配送；Pijkq为车辆Kq从客户i到客户j的车辆碳排放量；Uijkq为车辆Kq从客户i到客户j间耗油量；qi为客户i的货物需求量；C1q为第q种车型的车辆运行的固有成本；C2q为第q种车型的车辆运行的油耗成本；C3为单位配送客户满意度带来的价值收益；C4为单位排放量的碳排放成本；α为配送车辆提早到达客户i的单位等待成本；β为配送车辆延误到达客户i的单位延误成本；dij为客户i到客户j的距离；vijkq为车辆kq从客户i到客户j的行驶速度；THijkq为车辆kq到达客户i的时间；TKijkq为车辆kq离开客户i的时间；ti为配送客户i所需的服务时间；tij为客户i到客户j的运输时间；tijkq为车辆kq在客户i到客户j间的行驶速度；φ为客户满意度与到达时间的函数关系系数。决策变量Xijkq=1时，车辆kq从客户点i驶向客户j，Xijkq=0，车辆kq不从客户点i驶向客户j；Yikq=1时，客户点i由车辆kq负责配送，Yikq=0时，客户点i不由车辆负责配送。

（二）交通线性背景下多目标城市配送路径优化模型

运输企业的配送成本是由车辆固有成本、耗油成本及配送的等待和延误成本构成，表示如下：

碳排放成本与碳排放呈正向相关关系，则碳排放成本为：

英国交通研究所研究表明，车辆从客户i到客户j行驶过程中的碳排放量和车辆行驶速度及距离有关系，具体为：

参考文献[6]，系数取（∂0，∂1，∂2，∂3）=（1.576-17.6，0.00117，36.067）。碳排放量Pijkq和耗油量Uijkq之间的关系为Uijkq=τPijkq（为碳排放量和耗油量的换算比）。

因此，交通限行政策下的城市配送多目标城市配送路径优化模型表示如下：

配送车要符合区域时段限行的政策：THikq≤TEi，TKikq≤TEi或者THikq≥TFi，TKikq≥TFi。（14）

四、算例分析

本文主要以某配送中心在西安三环内的配送情况为例进行案例分析。配送中心位于二环路附近，工作时间为05∶00-24∶00，且拥有多种车型的配送车辆，负责城市内20个零售商的配送业务。参照西安市三环的面积比例，城市配送的范围设为20km20km。为对客户坐标进行清晰描述，将城市区域限定在100100的坐标中。一环范围为4km4km，设为区域1，二环范围为10km10km，设为区域2，三环设为区域3。各客户点的地理分布随机产生，假设客户点的货物需求量在0t-2t内随机不等分布。城市配送客户的坐标、服务时间、货物需求量、客户重要程度等信息如表2所示，其中序号0代表配送中心。

根据城市配送特性及环境要求，配送车辆设为中型、轻型及微型三种，且根据《机动车类型术语及定义（GA802-2008）》规定，设定城市配送车辆载重量分别为6t、3.5t及1t，数量不限，以保证满足城市配送量的要求。同时根据实际情况且参考部分城市的交通限行政策，案例分区域设定了不同车型通行时间限行政策，如表3所示。

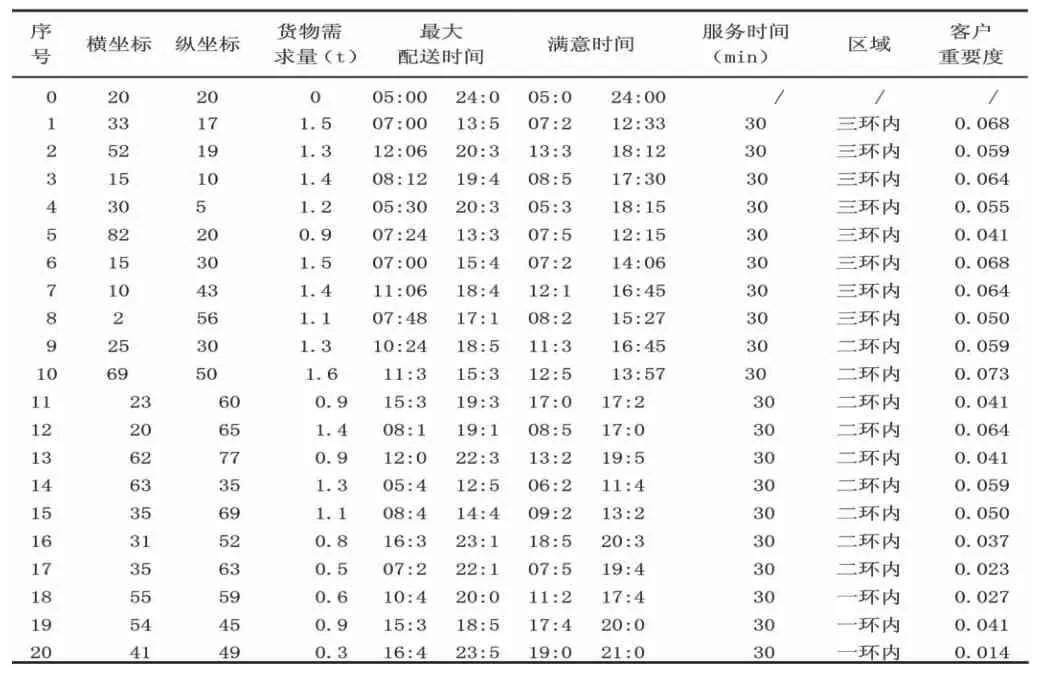
表2配送客户基本情况

表3各区域对于通行车辆的车型及通行时间限制情况

根据相关文献及实际车辆相关成本的大小将不同车型的车辆固定成本、油耗成本及时间惩罚成本、碳排放成本等参数的设定情况如下：

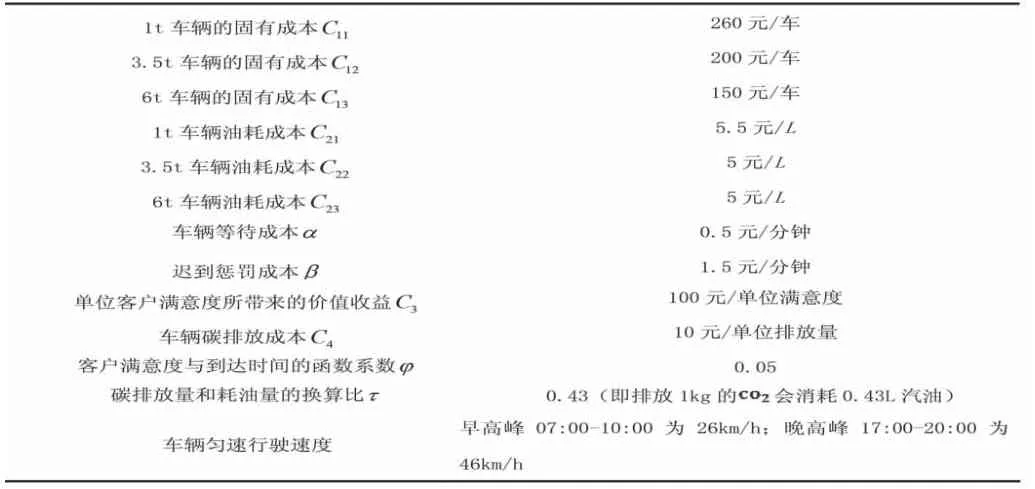
表4车辆相关成本情况

本文基于Java编程对交通限行政策下城市配送多目标车辆路径优化问题进行了仿真，得出在算例设定的交通限行区域及通行时间条件下，该城市配送企业对城市三环内各客户点进行服务的路线表5所示。

表5配送的优化路径方案

由路径优化结果来看，在保证不违反交通限行政策的情况下，配送中心根据客户重要度对分布在城市各环区的20个客户点进行配送，共优化出7条配送路径，使用2辆载重为1.5t的车辆、3辆载重为3.5t的车辆及2辆载重为6t的车辆，共配送21.9t货物。车辆实载率最高达到100%，最低为60%，配送车辆平均实载率为85.88%，车辆使用效率较高，能够有效的降低车辆空载率和使用成本，提高收益。

五、结论。

本文考虑了交通限行政策对于城市配送的影响，从三大利益主体的实际诉求出发，将城市配送的优化目标设定为配送成本、客户满意度、碳排放成本三方面，构建交通限行背景下城市配送多目标路径优化模型，并应用算例证明模型的可行性。未来，论文将针对多配送中心向多配送点配送情景对交通限行背景下城市配送路径优化问题进行更深入的研究。