面向用户协作对的移动群智感知激励机制
杨桂松,李汉卿,何杏宇
1(上海理工大学 光电信息与计算机工程学院,上海200093) 2(上海理工大学 出版印刷与艺术设计学院,上海200093)
1 引 言
移动群智感知[1]是一种利用大量用户所携带的智能终端设备随时随地感知和获取周围环境信息的方法[2].目前,移动群智感知已经催生了众多应用,如交通监控[3,4],环境监测[5-7],移动社交推荐[8,9]等.这些应用的成功运行离不开无数用户的感知行为.然而,在执行感知任务的过程中,用户消耗的是自己的资源,如电池电量、计算能力、时间等.为了合理补偿用户在感知过程中的消耗,以及提高用户参与感知任务的积极性,需要设计相应的激励机制[10],使尽可能多的用户参与到感知活动中,保证感知任务按时按需按量[11]完成.
激励机制的目标是激励尽可能多的用户参与感知活动.然而,由于平台的理想化以及用户的不确定性,使得传统的激励机制在用户招募方面遭遇瓶颈(更多具备一定感知能力的用户等待被发现),在报酬支付设计方面面临一定的挑战(如何同时兼顾平台与用户的利益).平台的理想化在于,平台默认能够参与感知任务的用户是能独自完成任务的用户,对于具备一定感知能力却又不足以独自完成任务的用户,直接排除他们参与感知任务的可能性.用户的不确定性在于,用户的感知能力取决于感知设备的能力,自身的感知时间以及对任务感兴趣的程度等因素.考虑到以上两点,移动群智感知中的任务的有效覆盖比例无法得到提升,进一步地,造成用户效用和平台工作效率低下.当前,大多数关于激励机制的研究工作假设平台将用户状态理想化[12-14],缺乏考虑具备感知资源但无法独自完成任务的用户类型,而非理想化的情况更符合实际场景.
为了解决上述问题,本文从感知时间的角度考虑,提出了一种面向用户协作对的激励机制.主要贡献如下:
1)研究并提出了移动群智感知的一个新问题,即如何充分利用资源较少的用户来提高移动群智感知系统的工作效率(用户参与比例,任务覆盖比例及用户平均效用).
2)提出协作对的概念,设计时间协作模型,旨在解决用户无法独自执行任务的难题.
3)提出基于斯塔克尔伯格博弈的激励方式解决了用户最佳报酬的问题,同时提高了协作用户的效用值.
2 相关工作
一些工作研究了不同类型的协作式感知问题.Lee等人在文献[15]中提出CoMon平台来解决最小化设备能量消耗的协作式感知问题.文献[16,17]从用户专业技能方面研究协作式感知问题,考虑招募具有不同专业技能的用户组成协作小组,共同完成复杂任务.文献[18]提出一种基于效用的节点协作感知方法以解决移动设备异构型与感知信息质量相矛盾的问题.与这些研究工作不同,本文考虑用户感知时间跨度受限的问题来进行协作感知设计.
在移动群智感知中,用户的报酬问题是激励用户参与感知任务的关键所在.Xiong等人设计的CrowdTasker[19]采用静态报酬与动态报酬相结合的方式.其中静态报酬是固定支付给感知用户的奖励;动态报酬则与分配给感知用户的感知周期数成正比.拍卖机制的利用也是基于报酬的激励机制设计的一大特点.Yang等人[20,21]分别采用Stackelberg博弈与拍卖机制设计了两种激励模型,以促使足够多的用户参与感知任务.前一种激励模型采用Stackelberg博弈理论,系统预先设定奖励金额,经过博弈确定任务执行者以最大化平台与感知用户的效益.后一种激励模型基于拍卖机制,在满足任务要求的前提下,用户提出可以接受的报酬底价,经过竞拍决定感知任务的执行者.文献[22]基于动态定价设计了新型的反向拍卖激励机制,利用用户声明的投标价格,将感知数据出售给合适的服务提供商.该机制能够降低极力拥护持续参与感知任务的成本,提高社会福利,并公平地给与用户报酬奖励.文献[23]设计了一个精确的激励机制,该机制让参与者在信息不完全的情况下进行贝叶斯博弈,以避免参与者出现虚假效用的局面,从而提高感知数据质量.文献[24]为了激励参与者,考虑了社会网络效应,并构建了不完全信息下的贝叶斯Stackelberg博弈模型来分析服务提供商和参与者之间的交互作用.文献[25]考虑了具有时间敏感性的数据收集场景,设计了基于讨价还价博弈的激励机制,并通过纳什均衡得到最大化收集者效用的解.
上述研究大都假设参与感知任务的用户能独自完成任务,没有考虑处于能力不足状态的用户也能参与感知任务的情况.激励机制的目标是促使更多用户参与感知任务,从用户角度来说,在预算一定的前提下,以最大程度发掘不同能力的用户为目标设计激励机制,会起到更好的激励作用.
3 时间协作模型

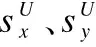
考虑到用户感知时间的高效利用,协作对的感知时间跨度在满足任务需求的基础上应该尽可能的小.为此,本文提出时间重叠率的概念,时间重叠率ORx,y由3部分组成:

2)后延:若用户Ux的感知时间跨度包含对应任务τj的结束时间,则该任务的结束时间到该用户的结束时间这段时间称之为“后延”,用afxj表示.
3)时间重叠:任意两个用户Ux、Uy的感知时间的重叠部分,用OLx,y表示.
本文将时间重叠率定义为3个部分之和与任务时间跨度的比值.该模型的目标是最小化协作对的时间重叠率:
(1)
约束条件为:
(2)
(3)
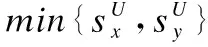
(4)
(5)
(6)
(7)
其中公式(2)表明,协作对的时间跨度不能小于任务的时间跨度;公式(3)表明,构成协作对的两位用户在感知时间上不能存在包含关系,且两者感知时间存在连接关系(第2位用户的开始时间小于或等于第1位用户的结束时间);公式(4)、公式(5)表明,协作对中的第1位用户的感知时间跨度要包含任务的开始时间;公式(6)、公式(7)表明,协作对中的第2位用户的感知时间跨度要包含任务的结束时间.
4 激励机制
4.1 协作对形成
协作对形成算法的过程如算法1所示,其具体描述如下:
1)用户主观协作意愿评估(算法1第1-3行)
用户的主观协作意愿是通过分析他们的实际兴趣得来的[26],而实际兴趣又与浏览行为密切相关,包括浏览内容、浏览停留时长、浏览频率.为了评估用户的兴趣,采用浏览历史分析方法,其主要通过语义、标签等关键词来分析用户针对特定内容的浏览历史.本文利用浏览历史分析方法来分析用户在最近TB内的浏览行为,从而获得用户对感知任务的浏览次数和浏览停留时长,该感知任务与最后执行的感知任务趋于一致.在统计时间[0,TB]内,用户Ui对任务τj共H次浏览后的兴趣强度,即主观协作意愿为:
(8)
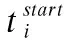
2)时间重叠率计算并择优(算法1第4-16行)
在遍历全部用户的过程中,满足任务类型相同、主观协作意愿达到阈值和用户感知时间跨度大于任务所需感知时间跨度这3点要求的协作对,对其进行时间重叠率计算.然后根据时间重叠率的计算值将选择合适的协作对作为相应任务候选执行者.
算法1说明协作对形成的过程.
算法1.协作对形成算法
1.输入:用户集合R1,任务τj
2.输出:协作对P
3.forifrom1ton
5.endfor
6.forifrom1ton
7.fori′fromi+1ton
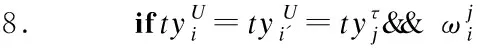
10. 将ORi,i′放入集合C中
11.endif
12.endfor
13.endfor
14.forORinsetC
15.ifORk,k′=min{C}
16.P=(k,k′)
17.endif
18.endfor
19.returnP
4.2 平台-协作对博弈
虽然通过4.1节得到的协作对是具有主观协作意愿的,但用户受到自身资源的限制,其会权衡收益与成本(进行感知活动的成本),从而导致用户可能不会主动参与协作感知.因此,为了进一步激励用户参与协作感知,本文从博弈论角度制定激励机制策略,提高用户的客观协作意愿.
协作对和平台之间的博弈是通过他们的报价来定义的.理论上,有序报价比随机报价能更快达到均衡价格.因此,引入斯塔克尔伯格博弈[27],并通过领导者和追随者序列的动态博弈改进随机报价方法.
给予协作对合理的奖励可以有效地激励用户的客观协作意愿,因此在博弈之前,应该定量分析协作对的感知成本.

(9)
(10)
(11)
2)博弈激励:由上文可知,用户在执行感知任务时会产生一定的资源消耗.根据用户的自私性,需要一定的报酬来对此消耗进行补偿.然而,用户一般是理性的,希望得到更多的报酬.同样,平台也是理性的,希望用尽可能少的报酬来获得用户的感知数据,因此,双方之间存在矛盾.为了解决这个矛盾,本文引入了基于有序报价的斯塔克尔伯格博弈,博弈后可以得到一个合理的支付方案,从而有效地激励用户的客观协作意愿.
斯塔克尔伯格博弈是一种完全信息动态博弈,在模型中存在“领导者”和“追随者”两种角色.在博弈的第1阶段中,平台作为领导者率先行动,根据任务的评估价值来决定报酬报价Φ,如式(12)所示:
(12)
式中,ε为感知平台统计的其他用户执行类似感知任务时,每单位时间内的最高成本.在第2阶段中,协作对作为追随者根据领导者的报价随后做出决策.
协作对P以最大化其收益为目标.因此,协作对P的效用函数可以被定义为获得的报酬减去成本,如式(13)所示:
(13)
其中,δ和δ′分别为协作对P中用户Ui和Ui′的单位时间成本.
分析斯塔克尔伯格博弈的方法是逆向归纳法.首先分析第2阶段,在这个阶段中,协作对根据报酬Φ进行博弈.如果平台和协作对都不能够通过单方面地改变策略来提高收益,那么在此阶段将达到纳什均衡(Nash Equilibrium,NE),从而使得协作对成功执行相应任务.随后,在第1阶段,平台选择合适的报酬Φ来最大化其收益.斯塔克尔伯格博弈具有如下均衡:
1)如果UP≤ 0,将不会有协作对成功执行相应任务.
2)如果UP>0,平台将会在第1阶段提供报价Φ.在第2阶段,协作对成功执行相应任务.
5 仿 真
为了评估面向用户协作对的激励机制(incentive mechanism based on user collaboration pair,简称IMUCP)的有效性,针对用户参与比例、任务覆盖比例、用户平均效用和协作率4个性能指标进行了仿真,仿真饰演的主要参数在表1中给出.

表1 仿真参数表Table 1 Simulation parameters
将IMUCP的性能与最小感知时间算法(The Minimum Sensing Time Algorithm,MSTA)和反向维克里拍卖算法(Reverse Vickrey Auction Incentive Mechanism,RVA-IM)[28]的性能进行比较.在MSTA算法中,根据适合指定任务类型且具备最小感知时间跨度的条件来选择单个用户.在RVA-IM算法中,在满足任务类型和感知时间跨度的条件下,出价第2低的用户将成为任务执行者,以此避免用户间的恶性高价竞争.以上3种算法均进行1000次仿真,并取其平均值用于仿真结果展示.
5.1 用户参与比例
图1显示了IMUCP和RVA-IM、MSTA的用户参与比例对比.从图1(a)可知,用户参与比例随任务数量的增加而升高.这是因为当任务数量相对于用户数量较少时,能够参与感知任务的用户也相对较少,因此3种算法下的用户参与比例均处于较低的水平.随着任务数的增加,能够参与到感知任务当中的用户数量也随之增加,因此用户参与比例随之上升.从图1(b)可以看出,用户参与比例随用户数量的增加而下降.
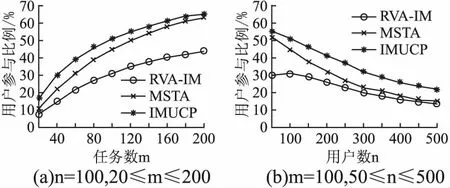
图1 用户参与比例对比Fig.1 Comparison of user participation ratio
这是因为在任务数量一定的情况下,用户数量的增加使得能够被用户执行的任务迅速饱和,导致大量的用户因剩余任务数量不够而处于无法参与感知任务的状态,从而使得用户参与比例下降.相较于RVA-IM和MSTA而言,IMUCP因为在单人覆盖任务的基础上实现了协作对协作覆盖任务,使得能够参与到感知任务当中的用户更多,因此用户参与比例始终处于高于RVA-IM和MSTA的水平.
5.2 任务覆盖比例
图2显示了IMUCP和RVA-IM、MSTA的任务覆盖比例对比.由于协同机制的存在,IMUCP在不同任务数量和用户数量条件下的任务覆盖比例都优于RVA-IM和MSTA.如图2(a)所示,随着任务数量的增加,3种算法下的任务覆盖比例都逐渐下降.这是因为在用户数量一定的情况下,能够执行任务的用户数量会达到饱和,后续增加的任务由于剩余用户不足而无法被执行,从而导致任务覆盖比例降低.从图2(b)中可以看出,在3种算法下的任务覆盖比例都随着用户数量的增加而升高.这是因为用户数量的增加可以直接提升任务被覆盖的概率,从而提升任务覆盖比例,直到被覆盖的任务达到饱和.

图2 任务覆盖比例对比Fig.2 Comparison of task coverage ratio
5.3 用户平均效用
图3显示了IMUCP和RVA-IM、MSTA的用户平均效用对比.总体来说,IMUCP的用户平均效用均高于RVA-IM和MSTA.这是因为相对于RVA-IM和MSTA的单人感知模式来说,IMUCP采用的基于斯塔克尔伯格博弈的协作对协作感知模式使得协作中的用户能够得到相对较高的报酬,因此提高了其用户平均效用.在图3(a)中,3种算法下的用户平均效用均随着任务数量的增加而减少.从用户参与比例和任务覆盖比例的仿真分析中可以知道,当任务数量增加时,用户参与比例逐渐升高,而任务覆盖比例逐渐下降,导致用户的人均报酬下降,从而减少了用户平均效用.在图3(b)中,3种算法下的用户平均效用均随着用户数量的增加而增加.同样,从用户参与比例和任务覆盖比例的仿真分析中可以知道,当用户数量增加时,用户参与比例逐渐下降,而任务覆盖比例逐渐上升,导致用户的人均报酬上升,从而增加了用户平均效用.
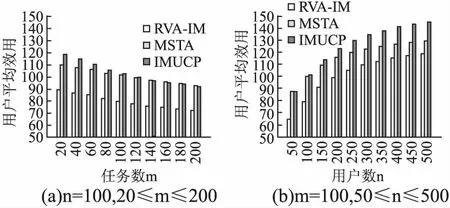
图3 用户平均效用对比Fig.3 Comparison of user average utility
5.4 协作率
图4显示了不同的任务数(用户数)和任务单位时间预算对IMUCP协作率的影响.由图可知协作率随着任务单位时间预算ε的增加而上升,在ε=2时达到最大值,之后趋于稳定.这是因为ε的增大可以直接增加斯塔克尔伯格博弈的成功率,促使协作用户的效用值为正,进而提升了IMUCP的协作率.

图4 任务数(用户数)和任务单位时间预算对IMUCP协作率的影响Fig.4 Effects of the number of tasks (users) and task unit time budget on collaboration rate
6 结束语
本文研究了移动群智感知中的激励机制问题,提出了一种面向用户协作对的移动群智感知激励机制.本文基于两个用户之间的时间状态和主观协作意愿来获得这两个用户组成的协作对的协作状态,并筛选出协作状态最佳的协作对作为相应任务的执行者.设计了一种基于斯塔克尔伯格博弈的激励方式以充分激励协作用户的客观协作意愿,进一步激励协作用户参与协作感知.大量仿真结果表明,相比于RVA-IM、MSTA两个算法,本文所提机制是有效的并且在性能上表现良好.在未来的工作中,可以将从空间的角度来考虑用户的协作场景.同时,还将探索更多的博弈激励机制方法.

