二维测向系统中坐标变换方法及实时补偿技术
田德民,杨峥峥,张学成
(中国船舶重工集团公司第七二三研究所,江苏 扬州 225101)
0 引言
以雷达电子战天线基座为准的坐标系安装于舰艇平台时,若舰艇平台存在偏航、纵摇、横摇等姿态运动,这些舰载设备的坐标系与地理坐标就不再一致,其所获取的目标参数,特别是二维到达角信息就与平台姿态相关。要消除舰艇姿态的影响,通常有机械稳定和电气补偿2种方法。传统的机械稳定系统复杂,平台笨重,精度差,已经逐步被电气补偿方法所取代。电气补偿的方法是通过已知各坐标系关系、舰艇姿态信息、平台安装参数等,通过数学的方法进行解算。实时动态补偿技术可以利用实时信息,通过实时解算来补偿平台姿态等信息对参数测量的影响。
文献[2]对一维比幅测向系统中舰艇纵横摇对测向精度的影响进行了分析,给出了改进的技术措施,但未涉及二维测向系统。文献[3]探讨了传统纵横摇坐标变换的方法和不足,给出了改进的修正因子。文献[4]也对传统的舰艇纵横摇坐标变换进行了讨论,提出了存在的不足,给出了新的大地坐标与甲板坐标之间的变换矩阵。文献[5]对舰载雷达天线电子稳定方程及坐标变换矩阵进行了细致的推导和仿真工作,同时对各个文献中各参数的定义进行了分析和比较,给出了目前采用的不同方法虽然形式不同,但结论一致的推算结果,具有一定参照意义。文献[6]对三坐标雷达稳定平台剩余误差进行了修正,给出了修正公式;文献[7]从理论基础上介绍了不同坐标系、参照系以及雷达阵面方向余弦坐标系,对于二维干涉仪测向系统具有同样参考意义。文献[8]对舰载雷达常用稳定方式坐标变换进行了分析,并介绍了船用平台罗经的基本原理,从而解释了坐标变换旋转顺序的原因。文献[9]给出了不同坐标系之间的转换关系,对于舰载雷达及侦察系统的坐标变换具有一定的指导意义。文献[10]主要从欧拉角和姿态角的关系给出了一种舰艇载体坐标系到地理坐标系旋转矩阵实用算法。
一维测向系统只需给出方位角,姿态变换时只需将舰艇航向角参与到方位角解算。而二维测向系统给出的辐射源信息不但有方位角,还包括俯仰角信息,天线阵面安装时还可能存在倾斜角,所以在实现时就需要综合考虑天线阵面安装倾角、舰艇姿态等信息,参与到二维辐射源角度的解算中。
本文在参照以上文献的基础上,主要关注了舰载二维干涉仪测向系统中舰艇姿态、系统安装角度等参数动态处理方法,从坐标系转换和实时动态补偿的角度在工程上进行实现。
1 常用坐标系
舰载雷达电子战系统中几种常用的坐标系包括大地直角坐标系、天线方向余弦坐标、舰艇甲板直角坐标系,如图1所示。
1.1 大地坐标系
大地坐标系采用大地纬度、大地经度和大地高度来表示空间的点,在舰载雷达电子战系统中一般描述空间点采用的是方位角、俯仰角及高度几个参数,为简化后续引出的坐标变换的描述,本文中首先引出大地直角坐标系OXYZ见(图1(a))。
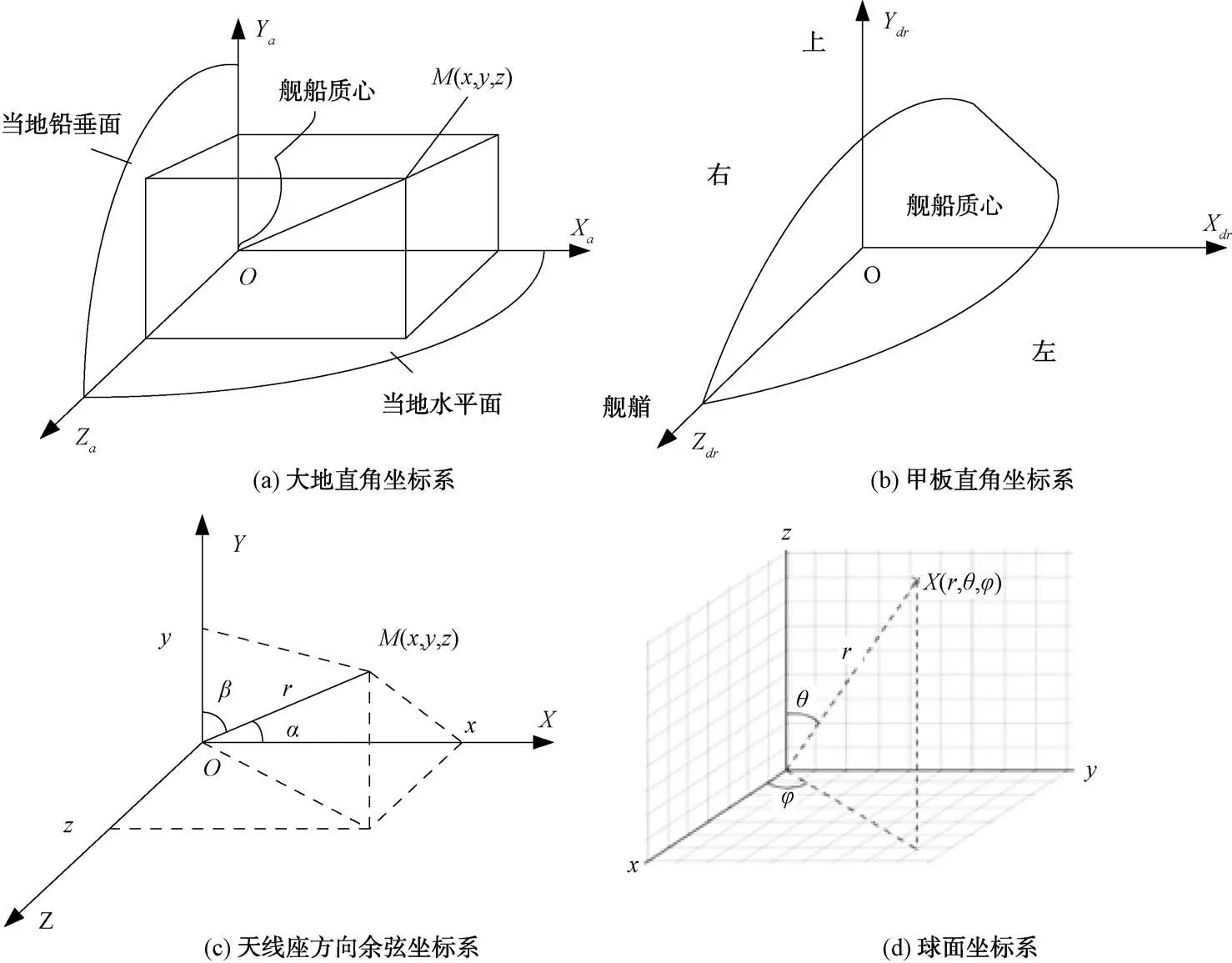
图1 各坐标系示意图
在该坐标系中,定义如下:Z轴指向地理正北方向;Y轴沿铅垂线向上;X轴与YZ按右手规则确定指向。
在大地直角坐标系中,轴X与Y构成当地水平面,轴Z与X构成的平面为当地铅垂平面。该坐标系的原点设在舰船的质心处,并跟随其运动。因此,更精确地说,这种坐标系为“当地”大地坐标系。大地直角坐标系是最常用的参照系,通常所说的目标与我舰的航向、速度以及风向、风速等,都是相对于大地直角坐标系而言的。通常雷达电子战主控台、舰艇平台罗经、显示终端等也都是以大地直角坐标系为参照系的。
1.2 甲板直角坐标系
如图1(b)所示,甲板直角坐标系OXYZ是一种动坐标系,其原点取在舰船质心处,各轴定义如下:OZ轴与舰体纵轴平行,指向舰艏为正;OX轴垂直于OZ轴,并与其在同一水平面上,指向左舷为正;OY轴垂直于OZ轴和OX轴,按右手规则确定,向上为正。
1.3 方向余弦坐标系
如图1(c)所示,在二维雷达和电子战系统中,常用方向余弦坐标系给出其测量值:
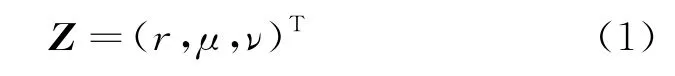
式中:为目标到原点的径向距离;,分别为目标径向与,轴的夹角的方向余弦。
设目标在雷达阵面直角坐标系中的坐标为,,,则方向余弦各参数表述为:
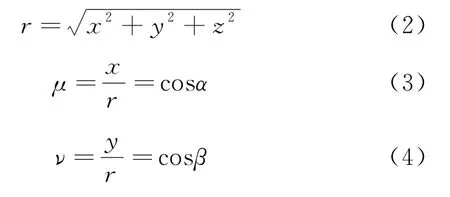
1.4 球坐标系
对于二维干涉仪测向而言,重点要测量的是俯仰角和方位角,不关心目标径向距离,所以需要利用球坐标的概念,传统球坐标系如图1(d)所示。3个参数(,,)表示一个点的球面坐标,各参数定义如下:为原点与点之间的径向距离;为原点到点的连线与正轴之间的天顶角,数值为90°-俯仰角;为原点到点的连线在平面的投影线与正轴之间的方位角。
球坐标系有着广泛应用,在天文学中,经度类于图1(d)中的,纬度类于(90°-)。实践中,球坐标中的角称为被测点(,,)的方位角,(90°-)称为高低角(俯仰角),这与我们在二维测向系统中给出的方位角和俯仰角的定义基本一致。
1.5 欧拉角
在探讨不同坐标系的变换之前,首先引出欧拉角的概念。欧拉角是用来描述刚体在三维欧几里德空间的取向所定义的角度,对于任何参考系,一个刚体的取向,是依照顺序,从该参考系做3个欧拉角的旋转而设定的。
如图2所示,设定轴为参考系的参考轴。称平面与平面的相交为交点线,用英文字母代表。顺规的欧拉角可以静态地这样定义:是轴与交点线的夹角;是轴与轴的夹角;是交点线与轴的夹角。

图2 欧拉角定义
但是,对于夹角的顺序和标记以及夹角的2个轴的指定,并没有任何规定。所以每当用到欧拉角时,我们必须明确地表示出夹角的顺序及其参考轴。
2 坐标变换
2.1 欧拉旋转定理
在运动学里,欧拉旋转定理表明,在三维空间里,假设1个刚体在做1个位移的时候,刚体内部至少有一点固定不动,则此位移等价于1个绕着包含固定点的固定轴的旋转。
2.2 坐标旋转变换
有了欧拉角和欧拉旋转定理,就可以用旋转矩阵的方式描述各坐标系之间的变换。对于本文所描述的二维干涉仪测向系统,当天线座安装相对甲板平面存在一个倾角,同时还要考虑舰艇纵、横摇和航向的影响时,需要首先进行天线坐标系到甲板坐标系的旋转变换,然后是甲板直角坐标系下的方位角、俯仰角利用舰艇纵摇角、横摇角及航向角经过坐标旋转变换,得到大地直角坐标下的方位角、俯仰角。
2.2.1 天线坐标系到甲板直角坐标系的变换

当完成天线坐标系与甲板直角坐标系之间的旋转变换后,二维测向系统中测得的方位角和俯仰角就变换为甲板直角坐标系下的方位角和俯仰角。
2.2.2 甲板直角坐标系到大地直角坐标系的变换

图3 天线直角坐标系与甲板直角坐标系关系图
舰艇的姿态由舰艇平台罗经提供的返回参数——横摇角、纵摇角和航向角所唯一确定,其定义分别规定如下:横摇角为甲板绕舰首尾线与水平面的夹角,右舷下降为正;纵摇角为舰首尾线相对水平面的转角,舰首抬高为正;航向角为舰首尾线与正北的夹角,自正北起.顺时针为正,定义区间为0~360°。
如图1(a)与(b)所示,开始时设定甲板直角坐标系与大地直角坐标系完全重合,甲板直角坐标系相对大地直角坐标系旋转3次,便形成3个欧拉角、、。根据欧拉旋转定理,同时参照文献[8]对平台罗经工作原理的描述,假定舰船先转航向,再纵摇,后横摇时(如图4(a)、(b)、(c)所示),则大地直角坐标系与甲板直角坐标系之间的变换关系可按下述内容计算。
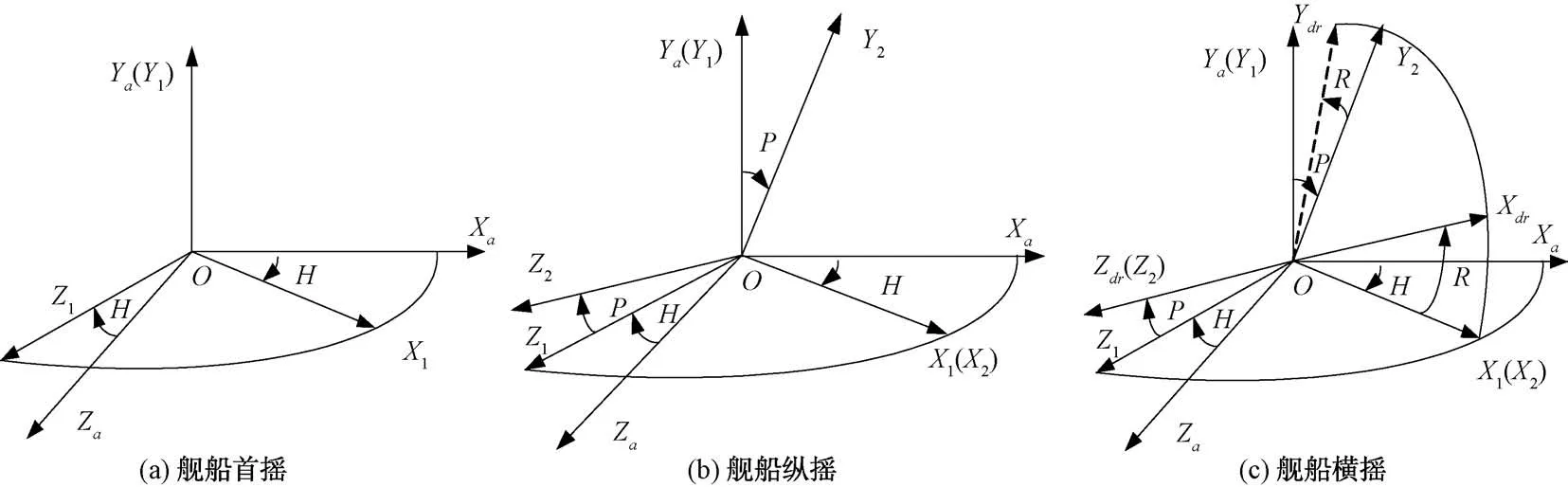
图4 大地坐标系与甲板坐标系之间变换关系
第1次甲板坐标系绕Y轴旋转1个角度,且顺时针为正,甲板坐标系由OXYZ旋转到位置。设空间某点在坐标系OXYZ和坐标系中的坐标分别为x,y,z和,,,则这2组坐标之间的关系可表示为:
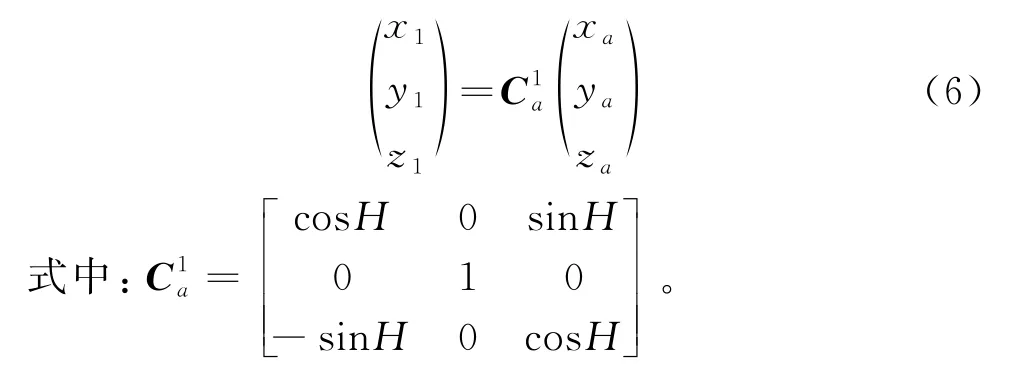
第2次绕旋转1个角度,甲板坐标系由旋转到位置。同一空间点在坐标系OXYZ和坐标系中的坐标分别为,,和,,,则这2组坐标之间的关系可用以下矩阵表示:
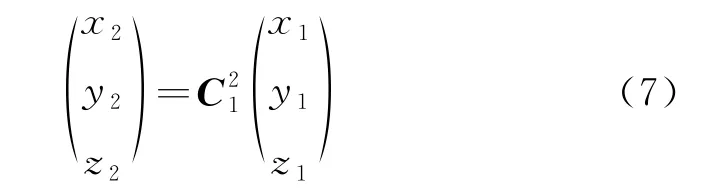
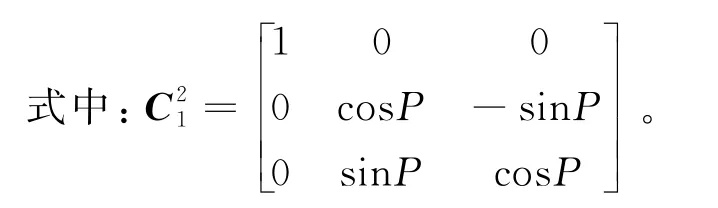
第2次绕轴旋转1个角度,甲板坐标由旋转到OXYZ位置。同理可以得到:

由式(6)、(7)和(8),甲板坐标系与大地坐标系之间的变换可以表示为:
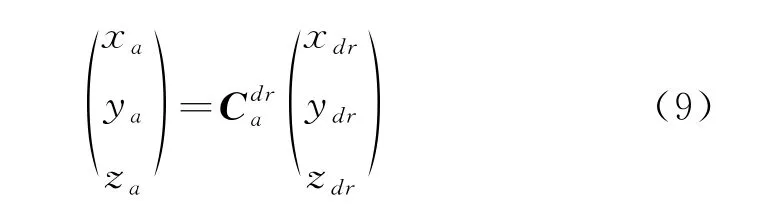
其中:

结合大地直角坐标与空间球面坐标系的变换关系式(1),并利用坐标旋转变换,将天线坐标系下测得的参数变换为大地直角坐标系下的参数。
3 实时坐标变换的工程实现
下面以二维干涉仪测向为例,讨论一下坐标变换实时补偿技术的具体实现。在许多文献中都对二维干涉仪测向俯仰角和方位角进行了定义,同时对解算步骤进行了分析,在此不再赘述。从本文的角度,最终要得到大地坐标下的方位角和俯仰角,分为以下3个步骤:
(1) 按二维干涉仪测向算法解算得到天线坐标系下的方位角和俯仰角;
(2) 引入天线倾角,按天线坐标系变换到甲板坐标系下的解算方法解算得到甲板坐标系下的方位角和俯仰角;
(3) 将甲板坐标系下的方位角和俯仰角继续进行坐标变换,解算得到大地坐标系下的方位角和俯仰角。
在步骤(1)中,以1对互相垂直的干涉仪为例,其公式仅列如下,具体不再推导:
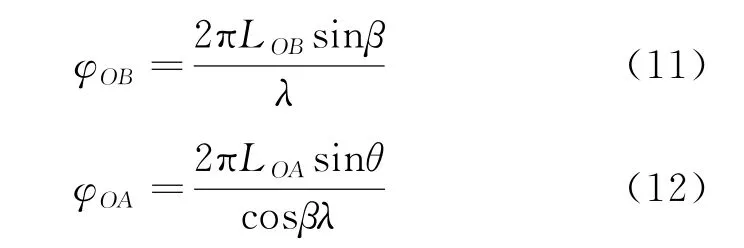
式中:为方位角,定义为入射信号投影与轴的夹角;为俯仰角,定义为入射信号与水平面的夹角;
通过先解算俯仰角,然后再解算方位角的方法就可以解算得到天线坐标系下的方位角和俯仰角。
步骤(2)中,按照公式(5)进行变换,因为在干涉仪测向系统中只能得到目标的方位和俯仰角,所以要用到目标的球坐标的概念,将公式中的、、变换为球坐标下,,,同时在此步骤中仅用到了,的三角函数,所以需要将步骤(1)的输出转换为三角函数。
步骤(3)中,按照公式(9)进行转换,同样用到球坐标的概念和三角函数。最终按照步骤(3)完成计算后得到的方位角和俯仰角需要解算反三角函数,而解算反三角函数快速准确的方法采用的是坐标旋转数字计算机(CORDIC)算法。
如图5所示,在天线坐标系下通过方位角和俯仰角解算得到天线坐标系下的方位角和俯仰角的三角函数值后,代入天线座倾角,进行甲板坐标解算,然后再引入航向角、纵摇角和横摇角,再次解算得到大地直角坐标系下的方位角和俯仰角的三角函数,最后通过CORDIC 算法解算得到大地坐标系下的方位角和俯仰角。
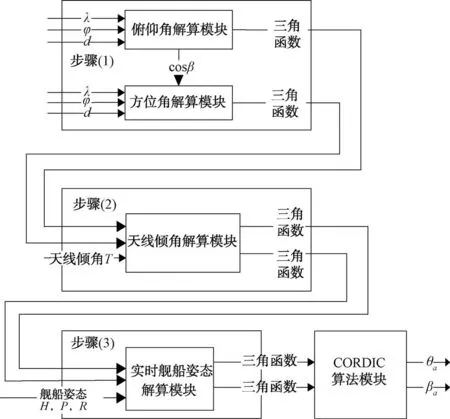
图5 二维干涉仪测向坐标转换实时解算框图
要实现实时的姿态补偿,所以设计中整个解算过程的3个步骤均在现场可编程门阵列(FPGA)内实现,其中三角函数的计算均采用了最快速的查表法,表中存储的为8位三角函数值,完全可以满足设计精度要求,整个解算过程用时小于200 ns。
4 结束语
针对雷达电子战系统装载平台的实时姿态信息对系统测向的影响,必须采用姿态补偿的方法将平台姿态信息引入测向处理中。本文从坐标变换的角度讨论了不同坐标系之间的转换方法及步骤,同时比对和讨论了各参考文献中的不足和局限,最后以坐标变换理论为基础,以舰载二维干涉仪测向为例,提出和实现了一种基于FPGA 的实时动态平台姿态补偿方法,并进行了工程实现。

