基于卷积神经网络的雷达点迹分类技术研究
齐永梅,刘正成,余承智,戴 霄
(中国船舶重工集团公司第七二三研究所,江苏 扬州 225101)
0 引言
在雷达目标环境中,目标以外的其他散射体的回波会使雷达显示器上的图像变得杂乱,妨碍对目标回波的检测,这类回波被称为雷达杂波。雷达目标和杂波的含义具有相对性,视雷达的用途而定。例如,地面回波对于防空雷达而言是杂波,而对地形测绘雷达则是目标;云雨回波对于气象雷达来说是目标,而对防空雷达则是杂波。对本文研究的舰载搜索雷达来说,舰船、飞机、导弹的回波为目标,而地物、海浪、云雨、岛屿的回波则为杂波。雷达在搜索和跟踪过程中不可避免地会受到地物杂波、气象杂波等影响,在信号处理检测时会产生杂波点迹,尤其是在杂波密集区,此类杂波点迹数量会更多,从而会建立大量的虚假航迹。在作战指挥时,如果态势中存在大量的虚假航迹必然会给指挥员的作战决策带来严重的干扰。由于杂波是不可避免的,信号处理和数据处理的一个重要任务就是尽可能地对杂波和杂波产生的疑似点迹进行过滤。
法国泰利斯公司研制的Master系列雷达自动化和智能化水平较高,能够实现对目标的全自动检测与跟踪,该雷达可实时监测背景环境,采用环境匹配技术(地形、海杂波、云雨杂波及干扰)自动调整雷达参数,并利用点迹多种特征信息对点迹质量进行综合评估,采用点迹过滤技术滤除杂波及干扰,提高雷达处理能力。目前国内雷达数据处理的自动化和智能化水平与国外相比还有一定差距,以深度学习为代表的机器学习技术并没有在数据处理领域得到充分的研究及应用。
深度学习概念是由Hinton等人于2006年初次提出,近些年它在各个领域大放异彩,成为人工智能(AI)领域中一个较为热门的话题。伴随深度学习技术的高速发展,不同分支的深度神经网络也得以在越来越多的领域进行应用。卷积神经网络作为其中之一,这些年不仅在架构性能上不断创新提升,而且应用领域也越来越广泛。卷积神经网络改变传统神经网络全连接的形式,通过引入局部感受野和共享参数的概念,大幅度减小了参数,并且提高了模型的性能。卷积神经网络结构通常有5个主要层次:输入层、卷积层、激励层、池化层和全连接层。
Tensorflow 是Google的深度学习框架,是利用人工智能神经网络来分析和处理复杂数据结构的系统,是一种支持深度学习的开源软件库,目前支持众多编程语言、操作系统环境和硬件架构(CPU 和GPU),可以实现卷积神经网络、循环神经网络和深度神经网络等经典算法。
本文提出用深度学习方法研究雷达点迹分类问题,以Tensor Flow 作为深度学习的基础框架,针对信号处理输出的点迹数据中混入的杂波数据,利用卷积神经网络判断该数据是更可能来自真实目标还是杂波,相当于对点迹质量进行评估,分类结果将为后续的数据处理提供技术支撑,减少杂波环境下虚假航迹数量,提高机动目标跟踪能力。
1 雷达点迹多维特征信息提取
在机器学习中,所有用于描述实体的数字的组合就是一个实体的特征向量,逻辑回归算法可以从训练数据中计算出每个特征和预测结果的相关度。特征向量的提取对机器学习的效果至关重要。如果每个特征和任务之间的关联不大,逻辑回归算法无法从数据中习得更好的特征表达。
目前,雷达点迹数据中最常用的信息为距离、方位、仰角等位置信息。其实,目标回波除了携带目标的距离方位仰角信息外,其波形还携带了与目标密切相关的信息。这些信息主要表现为随时间和作用距离远近呈现出渐变或者相对稳定的状态变化,我们称之为“特性信息”,主要包括目标在径向距离单元的跨度(或称之为距离宽度)、目标方位码跨度(或称之为方位宽度)、最大幅度、平均幅度、规整度等。
在大数据分析中,数据参数种类越多,所带来的信息就越多,就越有可能挖掘出更为有用的知识。当然,上述描述并不是严格成立的,前提是其参数必须是对解决问题有帮助的。因此,必须对于当前点迹信息中的所有参数进行分析研究,提取出对点迹分类有用的参数。通过整理,针对点迹数据,本文提取如下几种信息(包括位置信息、特征信息),具体如表1所示。
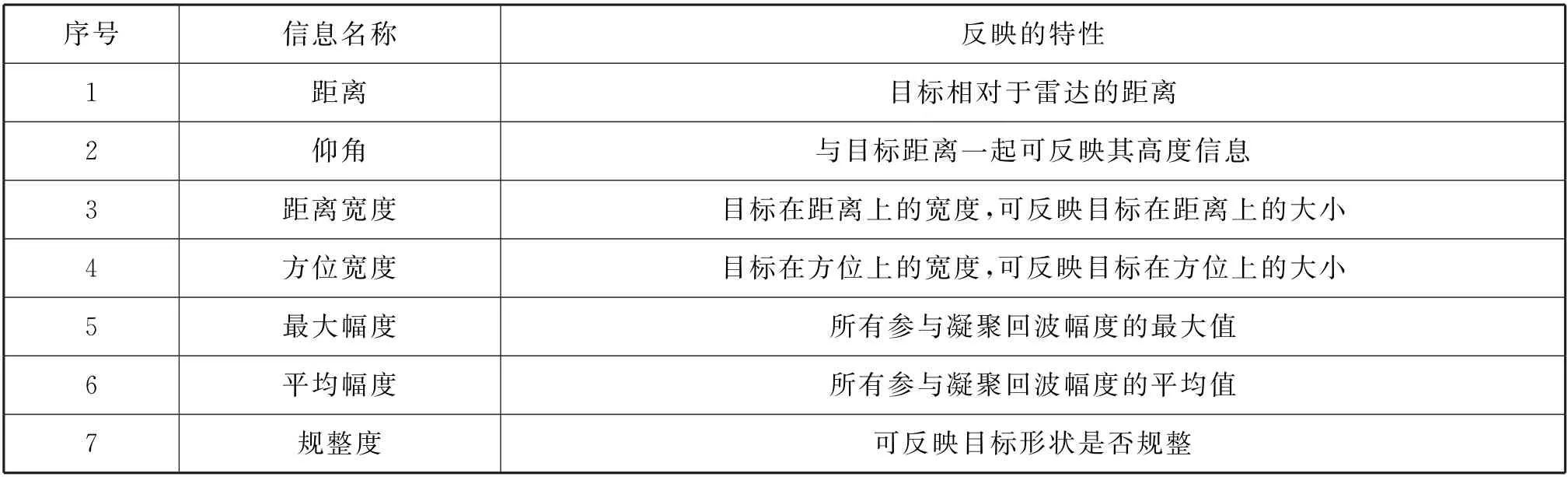
表1 点迹特征信息
(1) 距离和仰角
相对来说,雷达波束的仰角越低,数据中的杂波就越多,这是因为绝大多数的杂波均是由地物或海浪而引起的。另外,由于地球曲率的影响,舰载或陆基雷达视距大约40 km 左右。因此对于距离小于40 km 的点迹,其仰角越低,来自于杂波的可能性就越高。因此距离和仰角可作为评估点迹真假的特征值。由于杂波与目标点迹有可能来自任何方位,无法依据方位值判断点迹的真假程度,所以方位不作为点迹特征参数使用。
(2) 距离宽度和方位宽度
目标距离宽度和方位宽度从某个侧面反映了目标的尺寸大小。由于雷达所关注的目标多种多样,既有大尺寸的舰船,也有小尺寸的无人机。但相对于地物杂波来说,目标尺寸还是相对较小(如图1所示)。以距离宽度为例,在相同回波幅度条件下,点目标尺寸小、扩展少,地物杂波尺寸大、扩展多,方位宽度差异的产生原因与距离扩展类似。
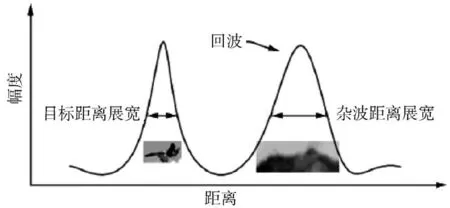
图1 目标和杂波的回波距离展宽原理示例
(3) 规整度
对于雷达所关注的常见目标(舰船、固定翼飞机、直升机、导弹)来说,其在距离、方位上通常呈现一定的规律,即相对规则的长方形,如图2所示。而对于杂波来说,常常并不是非常规则,如图3所示。

图2 民航飞机的回波视频
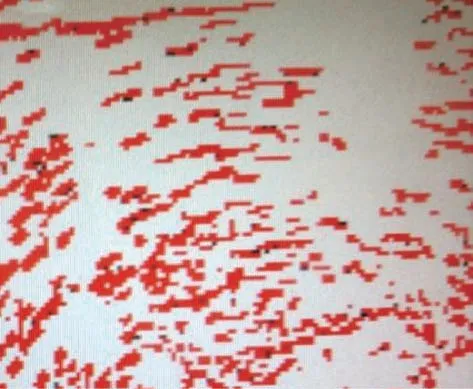
图3 杂波视频
为了能够更加直观地表述点迹视频的规则程度,现采用示意图的方式给出,图中每个“格子”为分辨单元,其中灰色为参与凝聚的过门限(该门限为信号处理恒虚警门限)视频数据,白色说明该分辨单元的视频数据没有过门限。
如图4所示,目标方位左右沿、距离前后沿可围成一个矩形,然后通过方位宽度(,单位°)、距离宽度(,单位m)、雷达扫描周期(,单位s)、重频(,单位Hz)、信号采样带宽(,单位MHz)即可计算出该矩形内所有分辨单元的数量():

图4 真实目标点迹视频示意图
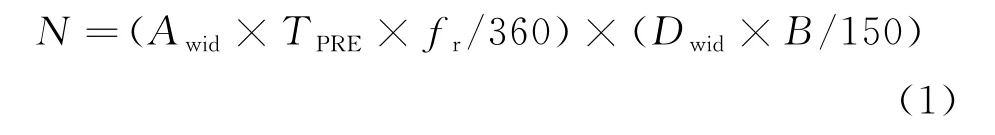
这时,可以引入一个概念“规整度”,即表示该点迹的规则程度,具体公式如下:
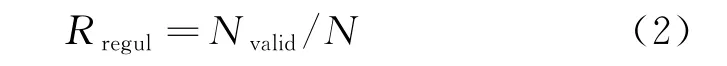
式中:为参与点迹凝聚的单元数量。
显然,规则度越高则点迹来自真实目标的可能性就越高,反之可能来自杂波。图5是杂波点迹视频示意图。
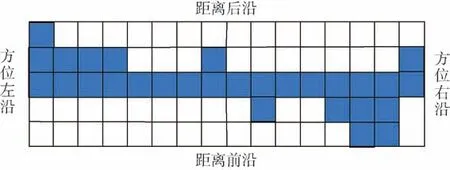
图5 杂波点迹视频示意图
2 基于卷积神经网络的雷达目标分类
2.1 数据说明
本文中使用的数据全部采用雷达实测点迹数据,根据剧情对数据中的每个点迹进行标注,杂波标签为0,目标标签为1。利用其中大部分数据对模型进行训练,再留一部分数据用于验证模型。本文中用于模型训练的数据集称为训练集数据,用于模型验证的数据称为测试集数据。
2.2 损失函数优化
判断一个分类器对所有样本的分类能力或者在不同的应用场合时,需要有不同的指标。在本文雷达杂波和真实目标分类问题研究中,漏警可能造成很严重的损失,也就是说将目标判为杂波的代价要远高于将杂波判为目标的代价。因此需要进行损失函数优化,对经典交叉熵损失函数进行加权。当目标被判为杂波时,代价权重为0.9;杂波判为目标时,代价权重为0.1。加权交叉熵损失函数为:
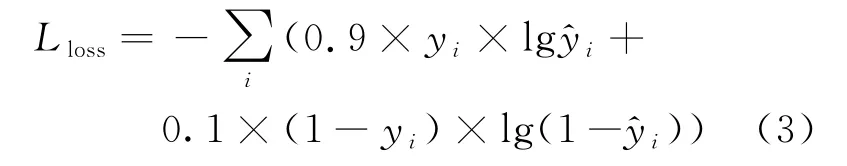
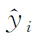
2.3 模型效果评估指标
本文综合利用准确率、目标损失率和杂波滤除率评估卷积神经网络模型效果。经过前述分析,针对本文应用场景,在降低目标损失率的前提下,尽量提高准确率或者说是杂波滤除率。为了对这3个模型效果评估指标进行说明,作出如下定义:“目标”是正类别,“杂波”是负类别。
可以使用表2来概括“杂波预测”模型,里面描述了所有可能出现的结果(共4种)。
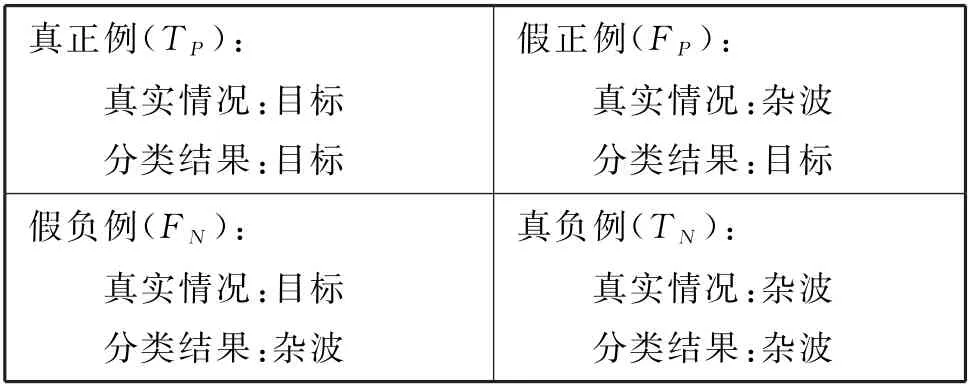
表2 “杂波预测”模型结果
准确率是一个用于评估分类模型的指标,是指模型预测正确的结果所占的比例,公式如下:
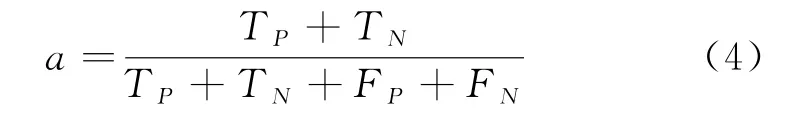
在本文场景中,目标损失率是一个重要指标,优化损失函数目的也是为了尽量降低目标损失率,公式如下:
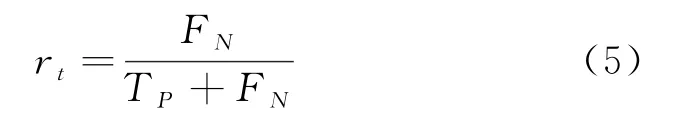
在降低目标损失率的同时,要尽量滤除杂波,其公式如下:
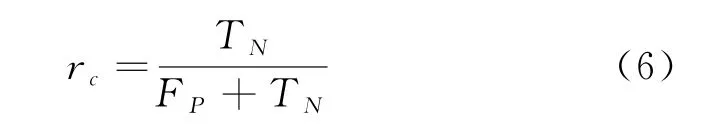
2.4 训练过程
本文中卷积神经网络的结构形式为输入层→卷积层()→卷积层()→池化层→卷积层()→卷积层()→池化层→全连接层→输出层。表3是卷积层所用的卷积核个数、卷积核宽、步长以及填充情况。
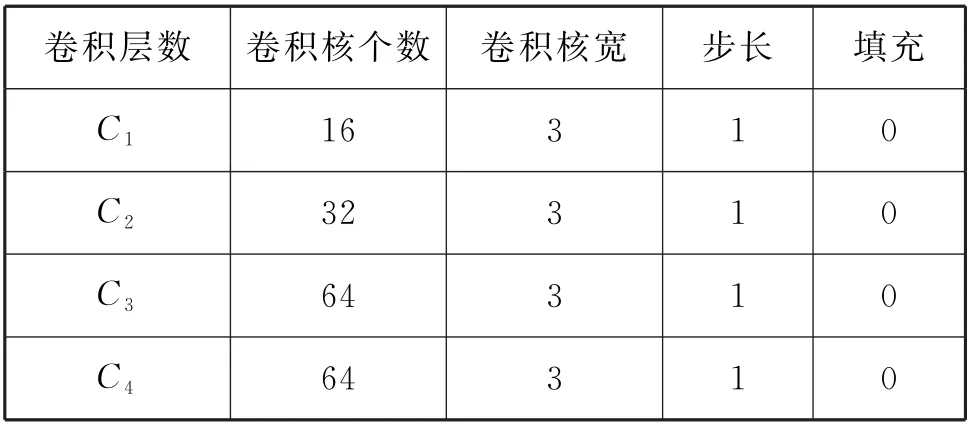
表3 卷积神经网络结构参数
作为神经网络输入的特征向量直接从点迹文件中获取,激活函数为ReLU 函数,最大池化方法,损失函数则为期望输出与真实输出的加权交叉熵。用于网络训练的训练集有6 400 个数据,验证集为2 000个数据。训练流程如图6所示。
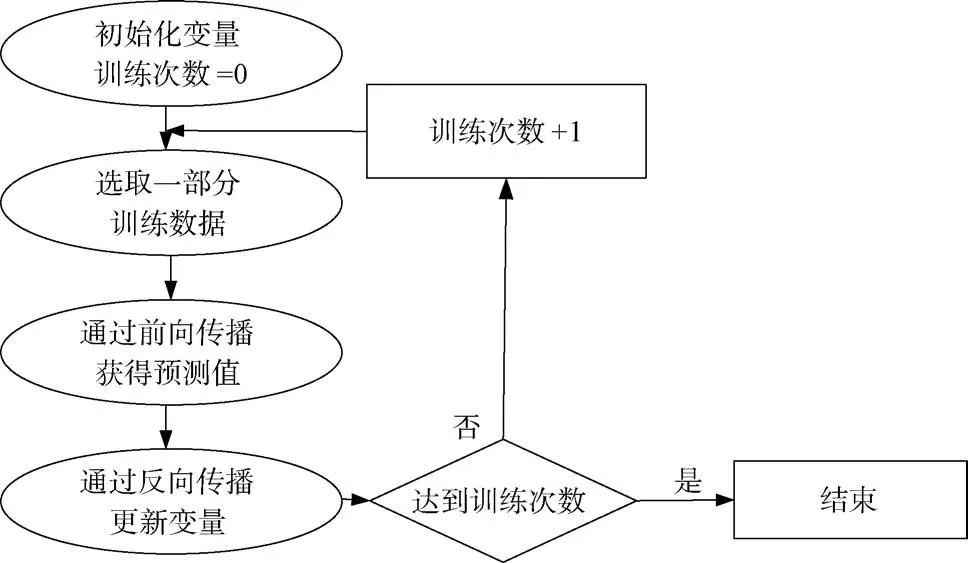
图6 训练流程图
步骤如下:
(1) 初始化。初始化训练次数为0,将网络的连接权值和偏置量均初始化为随机值,初始学习速率为0.001,每训练10 轮后学习率乘以衰减系数0.99。
(2) 前向传播。从训练数据集中随机抽取128个特征数据输入网络,逐层计算各层网络的输出,获得预测值。
(3) 反向传播。得到输出层的真实值后,根据优化损失函数计算真实值与数据标签的误差,更新网络连接权值和偏置量。
(4) 迭代训练。当训练集中所有数据都被抽取训练,完成一次迭代训练,训练数加1。然后使用当前状态的网络对测试数据集进行分类,得到分类准确率、目标损失率和杂波滤除率。80 次迭代训练后,停止训练。
3 训练结果
每次迭代后打印结果,训练集和验证集数据准确率、损失函数以及学习率随迭代次数变化如图7所示。
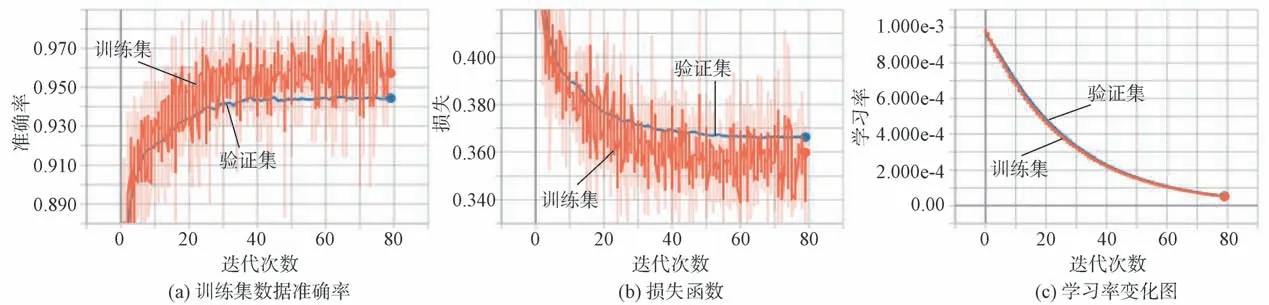
图7 训练集数据准确率、损失函数和学习率变化图
图8是最后几组迭代结果截图,图9和图10是 目标损失率和杂波滤除率随迭代次数变化图。

图8 最后几组迭代结果图
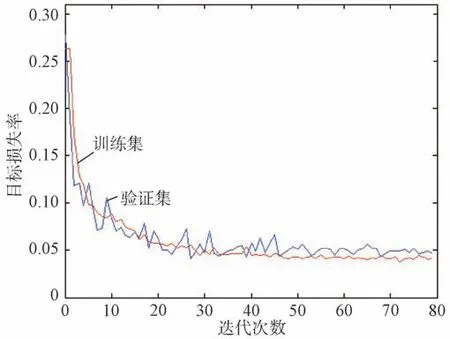
图9 目标损失率变化图
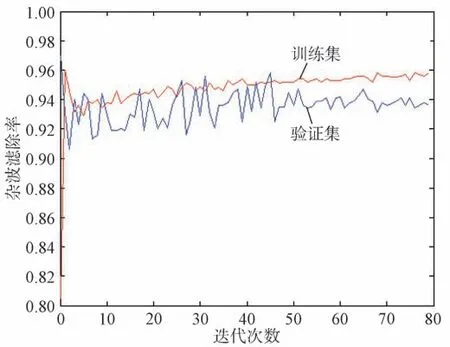
图10 杂波滤除率变化图
优化损失函数后,经过多次迭代,目标损失率只有0.04左右,杂波滤除率为0.93左右,准确率也达到0.94左右,表明提取的雷达点迹多维特征信息以及用卷积神经网络的方法能够对雷达点迹进行分类。
4 结束语
本文利用卷积神经网络研究雷达点迹分类问题,对雷达点迹质量进行评估。根据工程经验提取雷达点迹多维特征信息作为输入,针对性地优化损失函数,通过测试集数据验证模型效果,在高准确率的同时使目标损失率下降到可接受范围。
当有点迹数据时,利用本文保存的卷积神经网络模型对点迹进行分类,分类结果可以为后续的航迹起始以及虚假航迹剔除提供技术支撑,最终达到减少杂波环境下虚假航迹数量的目的。

