基于季节性ARIMA模型的中国货物周转量短期预测

摘  要：交通运输业的发展对国民经济具有先导作用，利用过去的货物周转量预测未来值，有利于反映物流产业发展趋势。基于国家统计局公开的2012年1月至2020年12月共9年中国货物周转量月度数据，分别选用简单季节ARIMA模型和乘积季节ARIMA模型进行拟合，并预测2021年1月至12月的货物周转量数据。使用两种模型进行预测的平均相对误差均较小，并且乘积季节模型的预测能力优于简单季节模型。

关键词：货物周转量;简单季节模型;乘积季节模型;ARIMA模型;残差诊断

中图分类号：TP391        文献标识码：A文章编号：2096-4706（2022）03-0141-05

Short Term Prediction of China's Cargo Turnover Based on Seasonal ARIMA Model

LI Kexin

（South China Normal University， Guangzhou  510631， China）

Abstract： The development of transportation industry plays a leading role in the national economy. Predicting the future number by using the turnover of freight traffic in the past is beneficial to reflect the development trend of logistics industry. Based on the monthly data of Chinese turnover of freight traffic from January 2012 to December 2020 altogether 9 years published by the National Bureau of Statistics， this paper selects separately simple season ARIMA model and product season ARIMA model for fitting， and predicts the data of turnover of freight traffic from January to December 2021.The average relative errors of the two types of models are all lesser， and the prediction ability of product season model is better than the simple season model.

Keywords： turnover of freight traffic; simple season model; product season model; ARIMA model; residual diagnosis

0  引  言

貨物周转量是运输企业所运货物吨数与其运送距离的乘积，代表了在一定时期内国民经济各部门对货物运输的需求以及社会货物运输总量，而货物运输需求大小取决于社会经济的发展水平。国内学者张宝友在探究我国物流业与进出口贸易关系时，认为两者之间存在极大的相关性，并且物流业对我国进出口贸易的发展起到了推动作用[1]。因此预测货物周转量的未来趋势，对促进物流业发展和国民经济发展具有重要作用。

近年来，国内外有许多学者运用时间序列方法预测交通运输业的发展趋势。凯里·高（Gogh Carey）和罗布·劳（Law Rob）[2]在对客源数据进行建模时，分别使用十个时间序列模型进行分析，研究成果表明在有干预的情况下，季节性ARIMA方法预测的准确度最高。关于季节性因素的周期长度，童明荣等[3]学者在对公路运输量建立ARIMA模型时，使用最小二乘法估计参数得到趋势方程，并利用傅立叶周期分析得出长度为12的季节成分，将12个月作为季节性的周期。在季节性时间序列研究中，大多数直接采用乘积季节模型，关于简单季节模型（即加法季节模型）的研究却极少。事实上，时间序列中的季节效应、随机效应和趋势效应的关联方式各有不同，简单季节模型也同样适用于带有趋势性和季节性的时间序列。高孝伟等[4]学者在对季节指数进行计算时，认为在考虑长期趋势时，利用加法季节模型比乘积季节模型更加具有合理性。因此，我们需要根据时间序列数据的特点，并且结合模型的拟合效果选择最优的模型。

本文选取2012年1月至2020年12月的货物周转量月度数据。由于季节变动和经济发展的影响，货物周转量大多带有季节性和趋势性，因此选用季节性ARIMA模型进行拟合及预测具有一定的优势。本文对货物周转量分别进行简单季节ARIMA模型和乘积季节ARIMA模型拟合，还进行了残差的自相关检验，以判断拟合的模型是否有效提取信息。在短期预测部分，本文还对预测结果进行相对误差的计算，以此判断预测精度。

1  研究理论基础

ARIMA模型（差分自回归移动平均模型）是统计学家博克思（Box）和詹金斯（Jenkins）于20世纪70年代初提出的一种时间序列方法，在金融、农业、气象等领域已有较广泛的应用。该模型利用历史数据揭示随时间变化的趋势，因此具有一定的预测能力。

1.1  ARIMA模型基本思想

ARIMA（p，d，q）实际上是ARMA模型（自回归移动平均模型）的一种扩展形式[5]。其中，AR为自回归模型，p为自回归项;MA为移动平均模型，q为移动平均项;d为原始序列转化为平稳序列所需做的差分次数。绝大部分非平稳时间序列数据在经过多次差分后均可以转换成平稳序列，因此对差分后平稳的时间序列使用ARMA模型拟合即为ARIMA模型的建模方法。ARIMA（p，d，q）的数学表达为：

ϕ（B）=1-ϕ1B-ϕ2B2-…-ϕpBp

θ（B）=1-θ1B-θ2B2-…-θqBq

其中B为后移算子，dxt表示为原始序列xt经过d次差分后的序列，εt为t时刻的随机误差，是服从均值为0，方差为常数σ2正态分布的白噪音。ϕi为待估计自回归参数，θj为待估计移动平均参数。

1.2  扩展的季节性ARIMA模型

季节性ARIMA模型分为简单季节模型和乘积季节模型。简单季节ARIMA模型是指序列中的季节效应、随机效应和趋势效应之间是加法关系。而若序列的各种效应间有复杂的关联性，则加法关系不能重复提取其中的信息，应该使用乘积模型。记s为季节性差分算子，因而有：

sxt=（1-Bs）xt=xt-xt-s

简单季节模型（加法季节模型）：通常周期步长差分即可将序列中的季节信息提取完整，低阶差分即可将趋势信息提取完整，提取完季节信息和趋势信息之后的序列是一个平稳序列，可以用ARMA模型拟合[6]。先对序列进行适当d阶差分消除趋势项，再进行S步差分消除周期项，最后使用ARMA模型拟合随机性，模型结构为：

乘积季节模型：短期相关性用低阶ARMA（p，q）模型提取;季节相关性用以周期步长S为单位的ARMA（P，Q）S模型提取[6]。假设短期相关和季节效应之间具有乘积关系，乘积季节模型ARMA（p，d，q）×（P，D，Q）S结构为：

U（BS）=1-ϕ1BS-ϕ2B2S-…-ϕpBpS

其中，d为阶差分消除趋势项;S为周期长度;P为季节性自回归阶数;D为季节性差分阶数;Q为季节性移动平均阶数。

1.3  季节性ARIMA模型建模步骤

使用季节性ARIMA模型进行时间序列分析的步骤为：（1）绘制时序图，初步判断平稳性、趋势性和周期性。计算并绘制自相关函数图和偏自相关函数图，并且用单位根检验其平稳性（Augmented Dickey-Fuller test， ADF）。（2）对非平稳序列进行平稳化处理。若时序图呈现较强的趋势性和周期性，需要使用多阶差分和多步差分分别消除趋势性和周期性。为了确定季节性的周期，可以直觀观察时序图和自相关图，还可以使用傅立叶周期分析确定。（3）根据时间序列的自相关图和偏自相关图确定阶数，辅以AIC赤池信息准则和SBC贝叶斯信息准则进行调整，AIC或SBC值越小表明模型越好，通过多个模型的比较进而建立效果最好的模型。（4）对拟合的模型进行参数估计，判断变量是否通过显著性检验，若不通过则需要将变量剔除，适用剩下的变量重新拟合。（5）对拟合模型的残差进行假设检验，诊断残差是否为白噪声，即是否仍存在自相关和是否符合正态性。如果残差序列为非白噪声序列，则模型并没有完整提取序列中的相关信息，即残差中还残留部分相关信息，说明模型拟合得不够好。（6）使用通过了上述检验的模型进行未来数据的预测分析。绘制预测数据95%置信区间图像，并计算预测数据对真实值数据的偏离程度，判断预测效果的优劣。建模流程图如图1所示。

2  实验与分析

对货物周转量的准确预测，是正确分析货运供求关系，明确发展方向的关键。本文选取国家统计局网站[7]公开的2012年1月至2020年12月一共108个月度全国货物周转量数据进行分析。此外，对于某些年份12月官方数据缺失，本文使用全年累计值减去前11个月累计值得出12月当期值，数据偏差在可接受范围内。本文在此数据基础上运用SAS统计软件建立模型及预测。

2.1  序列观察

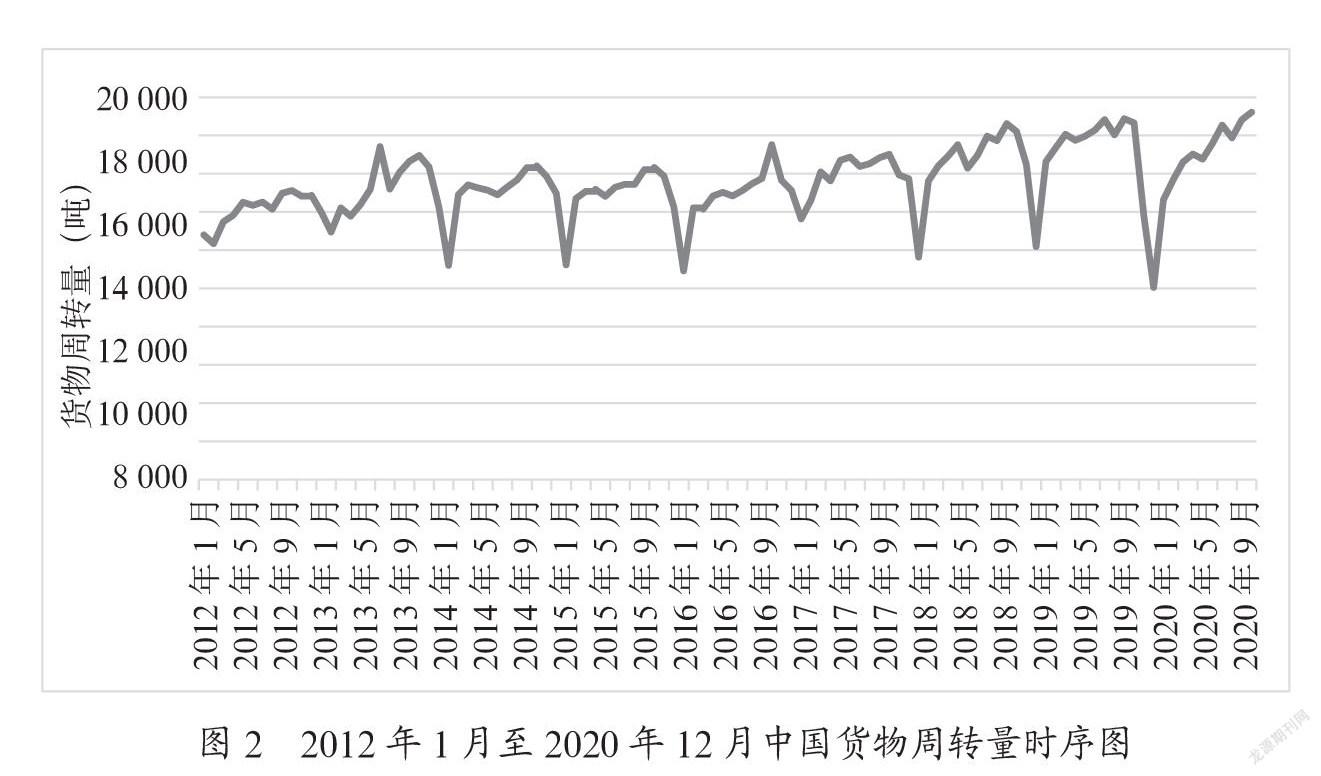
为直观观察时间序列的变化，制作出时序图，如图2所示。

从绘制的时序图直观判断，中国货物周转量数据在前五年的趋势性不明显，从第六年开始随时间增加呈现递增趋势，并且波动性也逐渐增大。此外，该序列有明显季节性，大致以12个月为周期。因此初步判断该序列为同时带有趋势性、季节性和随机性的非平稳时间序列，因此选用季节性ARIMA模型是适合的。

2.2  模型建立和检验

对原始数据进行一阶差分和十二步差分后，滞后6阶直至36阶均通过了ADF平稳性检验，并且在0.05显著性水平下拒绝白噪声假设，表明仍有部分信息未被提取出来，因此需要后续进行拟合，有继续分析的价值。差分后的序列为平稳非白噪声序列，满足使用ARMA模型进行拟合的条件。

计算ACF（自相关）值和PACF（偏自相关）值，并根据绘制的自相关图和偏自相关图的拖尾截尾性定阶，在0.05的显著性水平下剔除了不显著的参数，辅以AIC和SBC准则，选择最佳的简单季节模型和乘积季节模型分别为：

（1-B）（1-B12） xt = （1-0.560 79B）（1-0.450 44B12） εt

模型对应的AIC和SBC值如表1所示。

基于表1的结果，简单季节模型的AIC值和SBC值均大于乘积季节模型。根据AIC和SBC准则，在所有通过检验的模型中，使得AIC和SBC函数值达到最小的模型为相对最优模型。因此认为，在本文选取的中国货物周转量时间序列数据中，使用乘积季节ARIMA模型的拟合效果较好。

残差分析可以从两部分进行，一是判断残差是否仍存在自相关性，二是判断残差是否符合正态性假设。由表2可知，简单季节模型和乘积季节模型残差自相关检验的p值（Pr>卡方）均大于0.05，不能拒绝残差无自相关性的原假设，即表明残差无自相关性。残差正态性可由正态性检验的Q-Q图判断，残差大致分布在45°直线上，则可以认为残差基本符合正态性。若通过了正态性和自相关性检验则表明模型的残差中已无有效信息可以提取。在本文数据中，两种模型的残差均通过检验，拟合效果较好。

3  模型预测

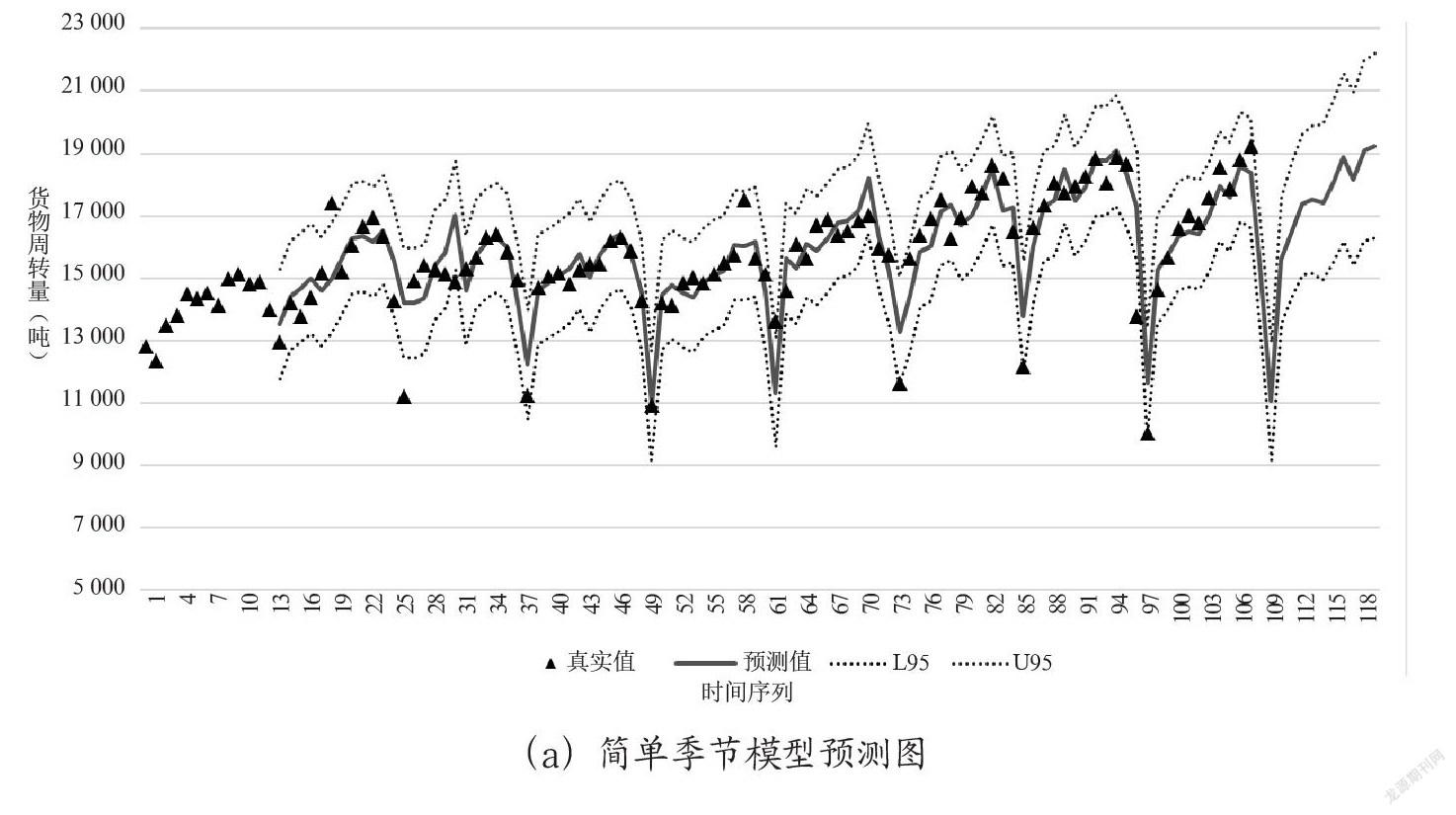
为了验证模型的短期预测能力，将拟合后的模型分别对2021年1月至12月的数据进行预测并作图。从图3（a）和3（b）中可以看出，简单季节ARIMA模型和乘积季节ARIMA模型预测值大致与真实值重合，并且波动性趋势也大致相同，说明两个模型较好地提取出了原始时间序列的趋势性、季节性和随机性，预测的效果较好。从预测图上无法直观判断两种模型的优劣，接下来对两种模型分别计算预测相对误差。

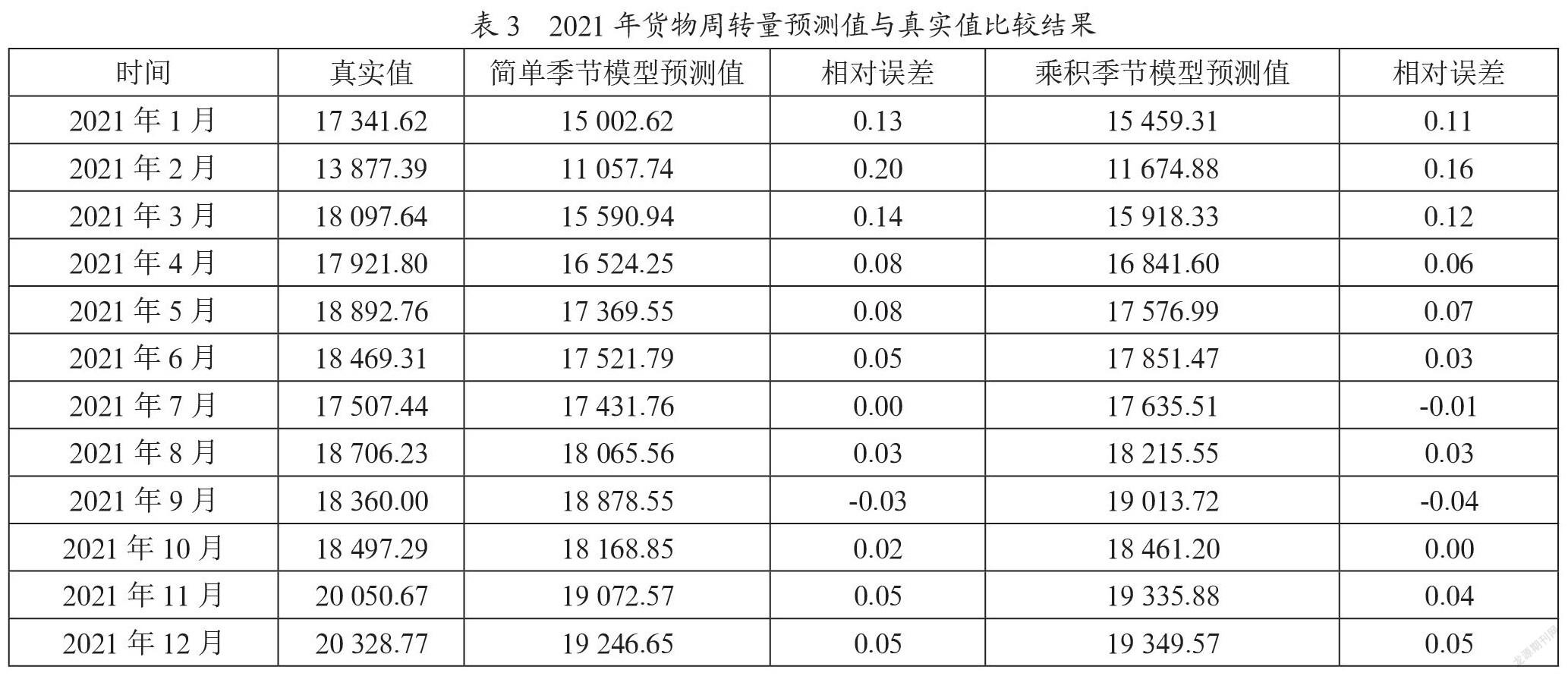
将真实值与预测值进行对比和简单计算得出表3所示数据，第一季度的预测效果相对来说较差，但6月之后的相对误差均在5%以内，总体预测能力可以接受。简单季节模型的平均预测相对误差为7.3%，而乘积季节模型的平均预测相对误差为5.9%。从经济意义上看，小于10%的预测误差都是可以接受的。因此这两个模型的预测效果都较好，而乘积季节模型在模型拟合效果和预测准确度上都比简单季节模型要好。

4  结  论

本文结论有以下两点：

（1）模型结论。在经济领域，ARIMA模型已取得良好的应用。本文尝试使用简单季节ARIMA模型和乘积季节ARIMA模型进行货物周转量的短期预测，结果显示两种模型均具有较好的实用价值。一般认为当时间序列数据的季节变动大致相等时，或数据随时间推移等宽变化时，使用简单季节模型即可，优点是模型表达和计算较简洁。反之，当季节变动与长期趋势大致成正比或同向变化时，应该采用乘积模型。本文选取的原始数据的季节变动相对一致，并且受趋势的影响较小，因此使用简单季节模型是可行的。综合上述实证分析，与乘积季节模型相比，简单季节模型虽然预测效果稍弱，但也有较好的应用价值，在实际中可以根据数据的特点和模型的复杂程度选择最适合的模型。此外，相比于单一模型，使用组合预测方法的预测精度更高。因此，为追求更高的预测精度，在模型的选择上面可以使用多种预测模型结合的方式，比如结合神经网络或者灰色预测。

（2）预测结果。从预测的数据来看，中国货物周转量的月度数据大致呈现趋势性和季节性。趋势性表现在从2017年开始的货物周转量具有递增的趋势，表明我国的物流产业有持续健康发展的趋势，进而表明国民经济在日益快速发展。季节性表现在每年的货物周转量具有相同的周期性，数值大致在每年的2月最低，11月最高，这与我国的国民消费习惯有关。2月为举国欢庆的春节假期，许多商家企业停工放假，因此货物周转量也相应减少。由于近年来的网购潮，11月各大商家对商品进行“双十一”的促销活动，巨大的优惠力度刺激着国民消费，进而刺激货物的周转量剧增。

从短期来看，国民经济部门和物流产业可以利用简单季节ARIMA模型和乘积季节ARIMA模型对未来的货物周转量月度数据进行预测，以提前了解未来物流的发展趋势，据此可以制定相应的政策和经营策略，以促进经济的持续健康发展。

参考文献：

[1] 张宝友.现代物流业对进出口贸易的影响——基于我国1995-2004年数据的实证研究 [J].国际贸易问题，2009，（1）：39-46.

[2] GOH C，LAW R. Modeling and forecasting tourism demand for arrivals with stochastic nonstationary seasonality and intervention [J].Tourism Management，2002，23（5）：499-510.

[3] 童明榮，薛恒新，林琳.基于季节ARIMA模型的公路交通量预测 [J].公路交通科技，2008（1）：124-128.

[4] 高孝伟，许涛，郑林昌，等.对季节指数计算方法的思考 [J].统计与决策，2006（9）：155.

[5] 熊志斌.基于ARIMA与神经网络集成的GDP时间序列预测研究 [J].数理统计与管理，2011，30（2）：306-314.

[6] 王燕.应用时间序列分析 [M].北京：中国人民大学出版社，2005.

[7] 国家统计局.国家数据 [EB/OL].[2021-12-03].https：//data.stats.gov.cn/easyquery.htm？cn=A01.

作者简介：黎可馨（2000—），女，汉族，广东梅州人，本科在读，研究方向：应用统计学。