第二大地边值问题引论
魏子卿
1.深圳大学,广东 深圳 518060;2.西安测绘研究所, 陕西 西安 710054
第二大地边值问题的边界面是已知的,因而称为固定边值问题。关于边界面外部的问题称为外问题,关于边界面内部的问题称为内问题。对大地测量而言,外问题更有意义。本文讨论的第二大地边值问题,实指它的外问题。
空间技术可以测量地面点的大地坐标——大地纬度、大地经度和参考椭球面的大地高。这意味着地形面以离散点大地坐标的形式就已知了。已知地面点的大地高,意味着该点的正常重力也已知了。如果已测量了地面点的重力,那么该点的重力扰动就等于是直接观测量了。边界面重力扰动的数学意义是扰动位在边界面外法线方向的负导数,而这正是第二大地边值问题的边界条件。
第二大地边值问题属于经典的Neumann问题[1-2]。空间技术的出现使这一边值问题的研究重新活跃起来。例如,20世纪60年代末,Hotine提出计算扰动位的Hotine公式[3];Bjehammar等证明边值问题解的存在性、唯一性和稳定性,并研究了垂线偏差的解法[4];文献[5]比较了计算大地水准面的Stokes和Hotine方法;文献[6—13]讨论了以地形面为边界面的第二大地边值问题的解法、地形改正等;笔者提出了边界面为参考椭球面的第二大地边值问题[14],等等。
第二大地边值问题的边界面可以是地形面,也可以是参考椭球面。两者应该是边界面最合逻辑的选择。这是因为,从地形面点沿椭球面法线向下量取一个大地高的距离,正是参考椭球面。如果地形面已知了,参考椭球面也就知道了。现代参考椭球是一个正常椭球。参考椭球面在物理上是正常位U=U0(常数)的等位面(水准面)。如果参考椭球面为边界面,它外部的地形质量必须移除。在这里,将这部分地形质量用Helmert第二压缩法压缩成无限薄层覆盖于参考椭球面[14]。同时我们还将地面重力扰动加地形(直接)影响改化为地面Helmert重力扰动,并用泰勒级数将其延拓至边界面得到椭球面Helmert重力扰动,作为边值问题的边界条件。
第二大地边值问题的解,或者是高程异常和地面垂线偏差,或者是大地水准面高和椭球面垂线偏差,或者是全部4者。这些术语如常,无须解释。这里有必要重提它们与地面点高程的关系。忽略垂线偏差,正高H、大地高h与大地水准面高N之间的关系是h=N+H。如果已知h和N,可得正高H=h-N。对于正常高H*,类似地有H*=h-ζ,这里ζ表示高程异常。这两个关系告诉我们,GNSS测量的大地高与第二大地边值问题得到的大地水准面高或高程异常,经简单线性组合,就得到了地面点的海拔高——正高或正常高,它们正是水准测量的产出。简单地说,大地边值问题的解加GNSS可代替水准测量。研究第二大地边值问题的动因之一就在于此。
本文原理性地讨论上述两种边界面的球近似第二大地边值问题。第1节和第2节介绍问题的边界条件、解法与解式,第3节是简单的讨论。
1 边界面:地形面
这种情况下,边界条件为边界面S上的重力扰动δg(X),X∈S,待确定的未知量为S外部空间Σ的扰动位T(X)=W(X)-U(X),这里W(X)和U(X)分别为点X∈Σ的实际重力位和正常重力位。球近似第二大地边界问题可公式化为
(1)
式中,∇2表示拉普拉斯算子,∇2=∂2/∂x2+∂2/∂y2+∂2/∂z2。
地形面不规则,也不是等位面。为方便计算,用规则的点水准面和参考椭球面来近似地形面。
1.1 地形面的近似:点的水准面U=UP
将任一点X的重力扰动δg(X)在地面点P的水准面处(图1),按z进行泰勒级数展开[6]
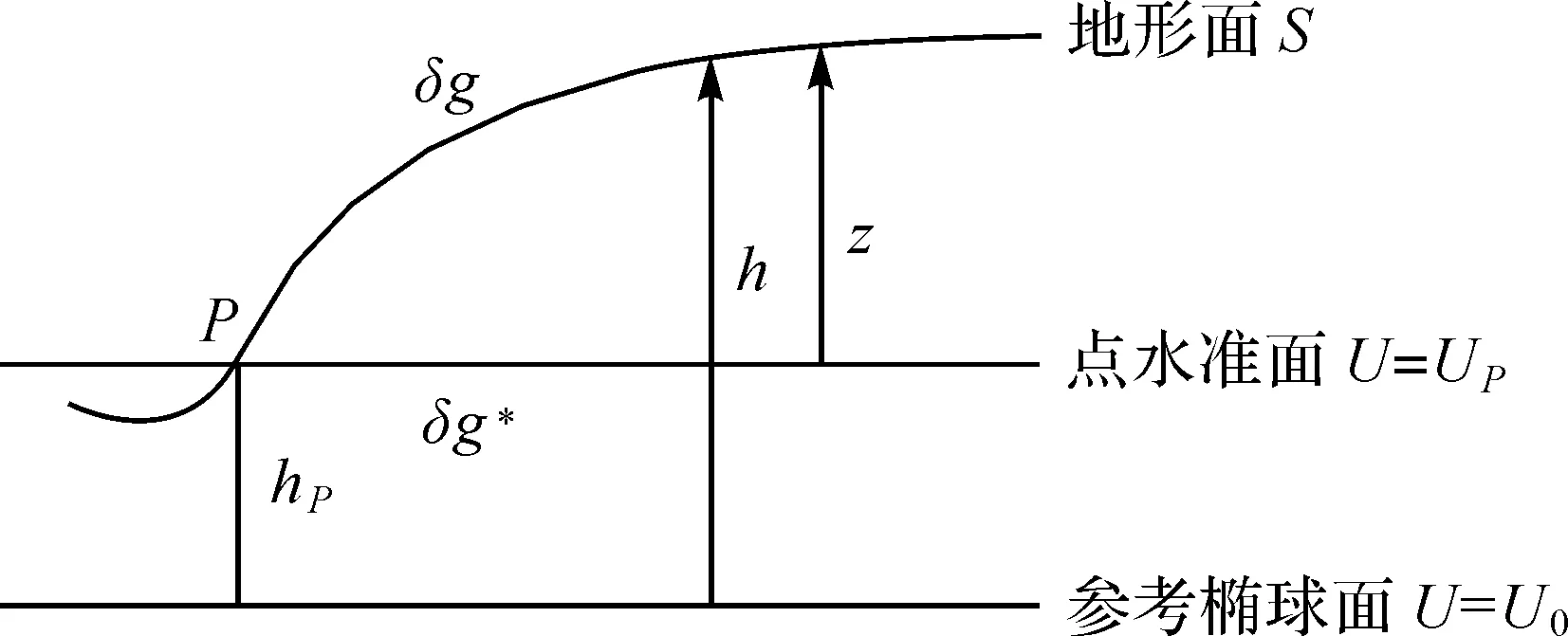
图1 从地球表面到点水准面的解析延拓
(2)
式中
z=h-hP
(3)
假定级数式(2)收敛,取至一次项,得到点水准面上的延拓重力扰动
δg*=δg+g1
(4)
其中
(5)
(6)
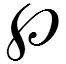
ψ=arccos[cosθcosθ′+sinθsinθ′cos(λ′-λ)]
(7)
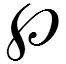
(8)
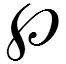
(9)
式中
l=((R+hP)2+r2-2(R+hP)rcosψ)1/2
(10)
将式(6)应用于地面点P(图1),则得点P的扰动位为
(11)
式中[3]
(12)
式中,ψPQP的算式参见式(7)。
用Bruns公式将T(P)转换为高程异常ζ
(13)
式中,γ代表似地形面(telluroid)上的正常重力。
T(P)转换为地面点P的垂线偏差,采用式(14)
(14)
式中[14]
(15)
1.2 地形面的近似:参考椭球面U=U0
根据Krarup-Runge定理[15],地球外部位总可以有足够的精度解析延拓至参考椭球面或海水面[6,16],据此用泰勒级数将地面重力扰动δg解析延拓到参考椭球面(图2)。
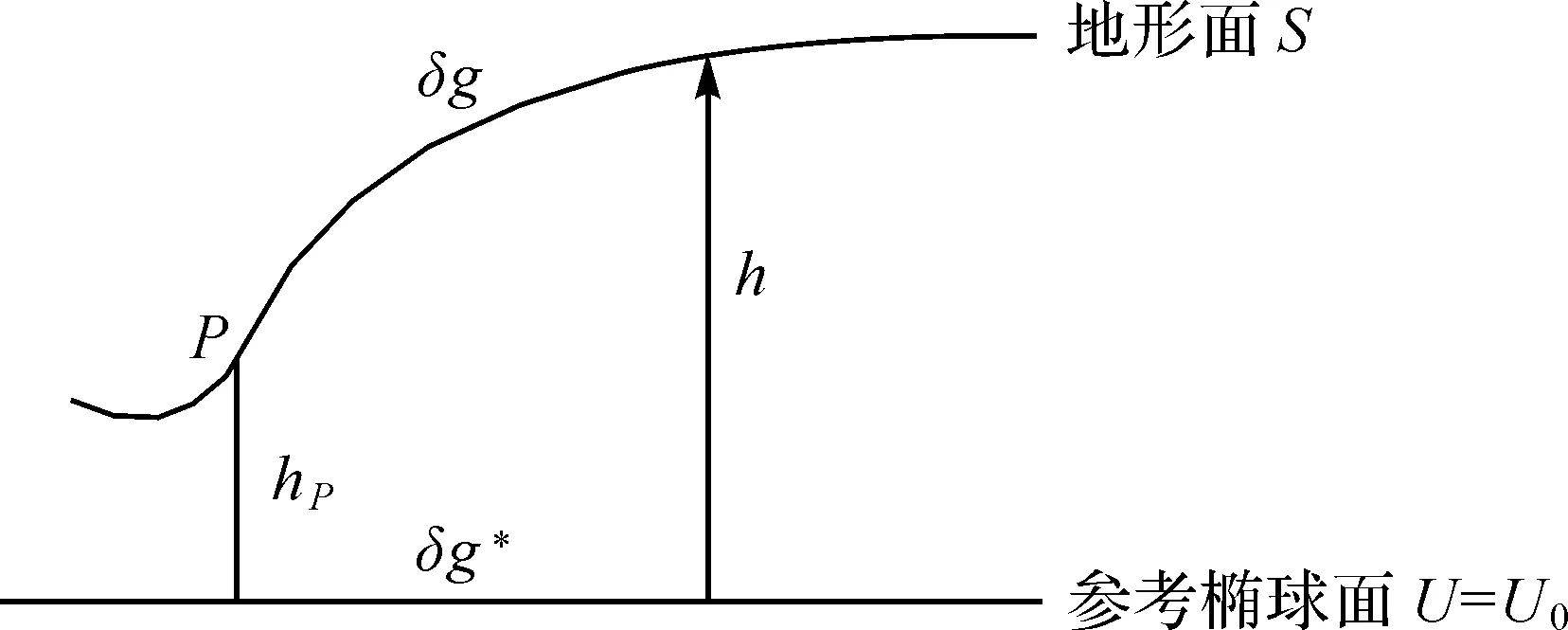
图2 从地球表面至参考椭球面的解析延拓
在参考椭球面上的延拓重力扰动是
δg*=δg+G
(16)
式中
(17)
当k=1时,有一阶延拓解,当k=1,2时,有二阶延拓解;当k=1,2,3时,有三阶延拓解,依此类推。经验表明,更高阶延拓解可以忽略。
(18)
式中
(19)
其中
l=(R2+r2-2Rrcosψ)1/2
(20)
式中,ψ的算式参见式(7)。
此时边界面仍是地形面,而式(18)的积分在参考椭球面上进行,Q0为参考椭球面的积分点。
将式(18)应用于地面点P(rp,Ω),则有点P的扰动位
(21)
式中
(22)
其中
(23)
式中,ψPQ0的算式参见式(7)。
地面点P的高程异常是
(24)
地面点P的垂线偏差是[14]
(25)
式中[14]
(26)
值得指出,根据调和函数的Stokes唯一性定理[16],式(11)和式(21)计算的同一地面点的扰动位应当符合在一定的范围内;同样,式(13)和式(24)计算的同一地面点的高程异常,以及式(14)和式(25)计算的同一地面点的垂线偏差也是如此。
2 边界面:参考椭球面
现在边界面为参考椭球面E,它外部的地形质量必须除去。为此,利用Helmert第二压缩法将E外部的地形质量向下压缩(移去)成无限薄层覆盖于E上(恢复)。地形质量的移去-恢复引起地面点P(图3)的引力位的变化为δV(P)=Vt(P)-Vc(P),称为残余地形位,这里Vt(P)表示E外部的实际地形质量在点P产生的引力位,计算式见附录中式(A1);Vc(P)为E上压缩薄层质量在点P产生的引力位,计算式见附录中式(A2)。
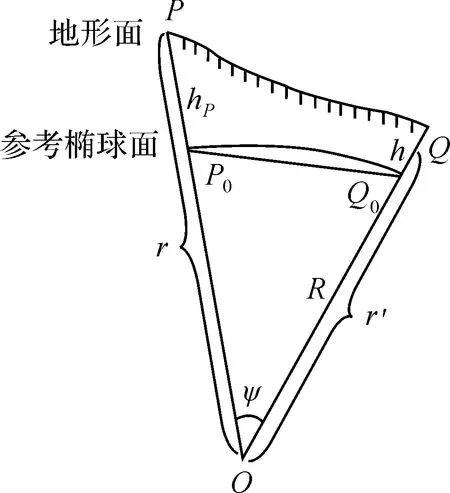
图3 地球表面上和参考椭球面上的计算点P和P0
地形质量的移去-恢复还引起点P重力的变化,称为地形的直接影响,对重力的改正是δA=∂δV(P)/∂r,这里r表示点P的地心向径。地形质量的移去-恢复引起一点引力位的变化,称为地形的间接影响,表现为对高程异常和地面垂线偏差的改正。
地面P点的实际重力扰动δg加上改正数δA,称为地面Helmert重力扰动δgh,即
δgh=δg+δA
(27)
用泰勒级数将δgh从地面延拓到参考椭球面E(边界面)
(28)
δgh*就是给定边界条件。待求未知量是E外部空间Σ′的扰动位Th(X)=Wh(X)-U(X),这里Wh(X)和U(X)分别为点X∈Σ′的Helmert重力位和正常重力位。此时球近似第二大地边界问题可公式化为
(29)
E外部Σ′任意点R(r,Ω)的Helmert扰动位Th是[14]
(30)
将式(30)应用于地面点P(图3)有
(31)
式中H(rP,ψPQ0)的算式见式(22);ψPQ0的算式参见式(7)。
将式(30)应用于点P0(图3),有
(32)
式中
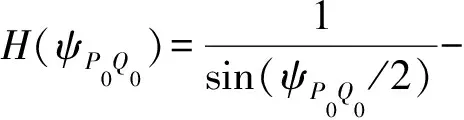
(33)
其中,ψP0Q0的算式参见式(7)。
用Bruns公式将Th(P0)转换为点P0的Helmert大地水准面(又称调整大地水准面)高Nh
Nh(P0)=Th(P0)/g0
(34)
式中,g0代表参考椭球面E附近的实际重力值[14],根据地面测量重力g用Poincare和Prey方法[16]向下归算得到。
点P0的真正大地水准面高N(P0)等于Nh(P0)加上地形间接影响δN(P0),即[14]
N(P0)=Nh(P0)+δN(P0)
(35)
式中
(36)
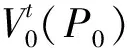
对于点P0的椭球面垂线偏差,有[14]
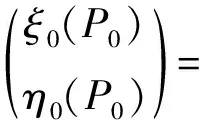
(37)
式中
(38)
高程异常是[14]
(39)
式中,Th(P)的算式见式(31)。
地面垂线偏差是
(40)
式中,∂H(rP,ψPQ0)/∂ψPQ0见式(26);ψPQ0的算式参见式(7);δV(P)=δVt(P)-δVc(P)。Vt(P)和Vc(P)分别为实际地形质量和压缩地形质量在点P产生的引力位,其算式见附录中式(A1)和式(A2)。
应当指出,用式(39)与式(13)及式(24)计算的同一地面点的高程异常应符合在一定的范围内;同样,用式(40)与式(14)及式(25)计算的同一地面点的地面垂线偏差应符合在一定的范围内。
还应当指出,正如所看到的那样,边界面为参考椭球面的第二大地边值问题,可以直接给出大地水准面高和椭球面垂线偏差。而边界面为地形面的第二和第三大地边值问题,没有这种能力。
现在回过头来推导偏导数∂δg/∂r。由于rδg是调和的[16,6],于是有
(41)
式中,δgn代表δg的第n阶分量,所以
(42)
对r微分,并令r=R,得在参考椭球面值
(43)
引用调和函数V的公式[16]
(44)
并令r=R与Yn=δgn,得
(45)
这就是重力扰动的垂直梯度公式。式中δgP参考于∂δg/∂r(对于球近似,∂δg/∂r=∂δg/∂h)的计算点P,l0是P0点与积分元之间的空间距离(图3),l0=2Rsin(ψ/2)
值得指出,式(45)的被积函数随距离增加而很快减小,所以积分范围可以限于计算点P附近。
还值得指出,式(45)对于Helmert重力扰动δgh与重力异常Δg同样适用。
重力扰动的更高阶径向导数式,见文献[14]中的附录B,那里给出了重力扰动的1—9阶径向导数式。
3 讨 论
目前广泛流行的Stokes问题和Molodensky问题属第三大地边值问题。前者的边界面是大地水准面,边界条件是大地水准面上的重力异常,定义为大地水准面上的重力与参考椭球面上的正常重力之差,解是大地水准面高和大地水准面垂线偏差;后者的边界面是地形面,边界条件是地面重力异常,定义为地面上的重力与似地形面上的正常重力之差,解是地面高程异常和地面垂线偏差。
Stokes理论发表于1849年,Molodensky理论诞生于20世纪40年代。当时测量技术只允许测量正高或正常高(这里统称“海拔高”),于是重力异常(不论是大地水准面上的,还是地面上的)是边界条件的唯一选择。用大地水准面高或高程异常与海拔高结合,可以得到测量技术难以给出的大地高。大地高是代表地球自然表面的地形面相对参考椭球面的高度。这是大地测量学研究地球形状的理据。
第二大地边值问题同样带有鲜明的时代特征。20世纪60年代以来,空间测量技术允许人们直接测定相对参考椭球面的大地高,地形面和参考椭球面均可以离散点的大地高形式测定出来。这意味着,第二大地边值问题的边界面,不论是地形面,还是参考椭球面,都是已知的。如果边界面是地形面,边界条件是重力扰动,问题的解是高程异常和地面垂线偏差;如果边界面是参考椭球面,边界条件是Helmert重力扰动,问题的解是大地水准面高和椭球面垂线偏差,还有高程异常和地面垂线偏差。倘若一点的大地高已经测得,该点的大地水准面高又已经算得,那么该点的正高就知道了;倘若一点的大地高已经测得,该点的高程异常又已经算得,那么该点的正常高也就知道了。这就是GNSS大地高结合第二大地边值问题解代替水准测量的概念。
第二大地边值问题,因边界面已知而属固定边值问题。第三大地边值问题,因边界面未知而属自由边值问题。理论上说,解自由边值问题需逐次迭代,实践中它常被当作固定边值问题解而不再迭代。相对而言,第二大地边值问题的边界条件和解法都较为简单,它的解会更好一些。本文给出它的球近似解,近似度在地球扁率级。在球近似基础上,加上椭球改正,近似度好于厘米级。或者,像国内外的经验证明的那样,用移去恢复技术结合顾及椭球项的全球重力场模型,球近似解也给出厘米级精度。
目前第二大地边值问题应用的一个限制是有GNSS大地高的重力数据有限。应当看到,这一情况在未来一段时间可能不会有大的改观。依笔者之见,在这种情况下,恰当的对策应当是,一方面既大力气获取更多新数据,另一方面也更加关注历史数据的有效利用。研究表明,用大地水准面高或高程异常的近似值(例如用全球引力位模型计算获得),改化现有重力点高程(从正高或正常高到大地高)的方案是可行的,高程改化并不至于严重伤及大地边值问题的解。
我们有理由看好第二大地边值问题的应用前景。毋庸置疑,它符合大地测量的发展方向。随着时间的流淌,这一趋势会更加明显。如果两方面都能做到更好,用第二大地边值问题解结合GNSS替代水准测量的目标是可以实现的。从长远观点来看,第二大地边值问题在这方面的表现很可能会胜过第三大地边值问题。

