基于测井数据的米氏旋回分析及浮动天文年代标尺的建立

徐敬领, 霍家庆， 宋连腾， 昝灵

1 中国地质大学(北京)地球物理与信息技术学院， 北京 100083 2 中国石油勘探开发研究院， 北京 100083 3 中国石油化工股份有限公司华东油气分公司勘探开发研究院， 南京 210019

0 引言

米氏旋回即米兰科维奇旋回，是指天文旋回导致气候(日照量)的周期性变化进而形成沉积韵律，最早由南斯拉夫学者Milankovitch(1941)在研究第四纪冰期旋回时提出，后来又被相关学者(Shackleton and Opdyke，1973；Hays et al.，1976；Berger, 1976, 1978; Berger and Loutre, 1991)通过大量的数据研究来证实.随着旋回地层学的不断发展，米兰科维奇旋回理论在地层划分对比、地层年代框架建立以及古环境古气候的研究中得到了广泛应用(李凤杰等，2008；王燕等，2019；吴怀春等，2008；Puetz et al.，2016；Westphal et al.，2004；贾泽南等，2019).总结前人研究米氏旋回的分析方法主要可分为两类，一类是岩性观察法(Weedon，2003；龚一鸣等，2004)，主要通过对钻井岩心或野外剖面的岩性岩相变化来观察分析，识别其中的米氏旋回记录.该方法识别米兰科维奇旋回存在一定困难，需要研究人员有丰富的经验与技能.另一类是时间序列分析方法，Weedon(2003)、郑民等(2007)、谢灏辰等(2016)采用快速傅里叶变换对研究区测井数据进行了频谱分析，识别出地层中的米氏沉积旋回，为沉积作用的分析和高频层序的划分提供依据.然而快速傅里叶变换的时域分辨力差，对于非平稳的实际测井信号序列来说，其无法分析米氏旋回沉积厚度在深度域的变化特征.袁伟等(2016)、杨雨等(2021)、刘浩童(2020)将傅里叶变换和小波分析方法相结合，两种方法的识别结果不仅可以相互对比验证，进而分析出米氏旋回在深度域上的变化特征，并计算沉积速率，最终精细地划分地层.然而该方法的研究重点还是在识别米氏旋回和划分地层上，没有进一步研究地层的年代学信息和建立高精度、高分辨率的时间地层格架.

为了从时间尺度上解决地球科学多个领域的关键问题，专家学者们开始寻找引起地质沉积周期变化的天文计时标准(汪品先，2006；吴怀春等，2011)，于是米氏旋回理论逐渐在浮动天文年代标尺的建立中得到应用.其中，Prokoph等(2001)利用米氏旋回理论，实现加拿大西部白垩纪Cenomanian-Turonian期界线附近地层连续的时间标定，估计了第二次大洋缺氧事件(OAE2)的持续时间约为320 ka.吴怀春等(2008)通过对松科1井南井青山口组的测井资料进行米氏旋回性分析，建立了青山口组浮动天文年代标尺，估计出青山口组1段底部发生的湖泊缺氧事件的持续时间约为250 ka，为后续研究青山口组沉积期的各类地质事件提供了年代学依据.魏小松等(2018)对北部湾盆地流沙港组沉积地层的自然伽马(GR)曲线进行米氏旋回性分析，并用锆石提供年代(时间锚点)，最终建立该地区的浮动天文年代标尺，为地层高频层序划分及提高油气勘探精度提供思路.邓秀芹等(2013)、张辉等(2014)、Wang等(2014)、张文等(2017)主要采用次离子质谱(SIMS)和激光剥蚀电感耦合等离子体质谱(LA-ICP-MS)等实验方法对鄂尔多斯盆地长7段开展了锆石定年分析，得到长7段年龄数据误差约为2.0 Ma；Zhu等(2019)通过锆石U-Pb ID-TIMS测年获得长7段相对精确的年龄为241.06±0.12Ma至241.558±0.093 Ma，数据误差范围约0.1 Ma，Chu等(2020)在此基础上研究了古气候、古环境与旋回，而基于测井数据研究长7段米氏旋回及沉积速率存在欠缺.以上天文年代标尺的建立有助于对研究区地质事件、古环境和古气候事件的持续时间做出精确估计，但都没有明确分析方法的原理、方法的可行性及从模拟的角度对米氏旋回分析的可行性做出探讨.

本文基于鄂尔多斯盆地B159井的测井数据，从傅里叶变换与小波深频分析的原理入手，通过数值模拟手段研究傅里叶变换和小波深频分析识别米氏旋回的可行性，再以B159井长7段的GR数据为研究对象，综合傅里叶分析和小波深频分析方法，识别出长7段地层中的米氏旋回，研究浮动天文年代标尺建立的方法，最终建立长7段地层的浮动天文年代标尺，为建立地层的时间格架提供一种高效的方法与思路.

1 米氏旋回频谱分析方法

1.1 米氏旋回数值模拟与频谱分析的理论基础

自然界中具有周期性的运动是普遍存在的.地层沉积的过程就是一个复杂的周期运动，它是由多个单周期的沉积运动叠加而成，每种周期的简单运动代表了这段地质历史时期所发生的沉积事件，它具有周期性、叠置性特点，表现为沉积物的结构、构造、岩性及岩相的周期性变化(郑民等，2007).测井信号本身也是一种由多信号叠加的复合信号，它记录了地层沉积的物质变化过程，能够敏感、连续地反映所测地层的旋回性、周期性等沉积特征，可以通过一定的方法技术提取地层旋回性特征，找出主要的周期，恢复地层的叠置韵律特征.

频谱分析是研究周期性事件的一种常见数学方法，其原理是利用傅里叶变换，把一条复杂的周期信号分解为一系列不同频率的正弦波或余弦波，找出其中振幅强度大且数学上呈现与米氏旋回周期相近的频率(胡丽莹等，2011).在实际工作过程中，采样是离散和有限的，因此在实际数据处理过程中都采用离散傅里叶变换，对于一段N项离散时间序列Xn，其离散傅里叶变换公式为

(1)

式中，Xk为频谱值，i为虚数单位，k=0，1，2,…，N-1.

而快速傅里叶变换(FFT)则是离散傅里叶变换(DFT)的快速算法，能迅速提高DFT的运算速度，使运算量减少两个数量级.

为了论证快速傅里叶变换识别米氏旋回的有效性，对米氏旋回做数值模拟研究.根据谢灏辰等(2016)、袁伟等(2016)用Berger法的计算结果：晚三叠世长短偏心率周期为404和123 ka，地轴倾角长短周期分别为44.3和35.4 ka，岁差长短周期分别为21.3和17.8 ka，首先模拟出周期分别为6个天文周期的正弦单信号曲线(如图4第二、三、四、五列)，然后将它们叠加，得到复合信号，该复合信号则可代表周期性沉积叠置地层的测量信号，最后对复合信号做FFT，如图1所示.图1左侧是6个天文周期的复合信号曲线，中间是对复合信号做FFT的结果，右侧是对复合信号做多窗口频谱分析(MTM)的结果.

图1 模拟的6个天文周期复合信号与频谱分析结果(a) 模拟的6个天文周期复合信号； (b) 复合信号的FFT分析结果； (c) 复合信号的MTM分析结果.Fig.1 The simulated composite signal of six astronomical periods and spectrum analysis results(a) The simulated composite signal of 6 astronomical periods; (b) The FFT analysis result of the composite signal; (c) The MTM analysis result of the composite signal.

分析图1中的复合信号曲线及FFT与MTM频谱分析结果得出：(1)6个天文周期组合的复合信号是比较复杂的，无法直观看出其包含的周期性信息；(2)通过对复合信号做FFT与MTM频谱分析，可以识别出复合信号所包含的有效频率信息，如：0.006、0.02、0.056、0.07、0.118和0.14个旋回/m，FFT与MTM对复合信号的分析结果一致，特别是6个尖峰频率是一样的，没有差异；(3)FFT频谱分析中的低频信号代表了长周期沉积的时间，如频率值0.006对应长偏心率时间404 ka，高频信号代表短周期沉积的时间，如频率值0.14对应短岁差时间17.8 ka；(4)该复合信号FFT频谱分析中含有6个主要频率信号，对应频率分别为0.006、0.02、0.056、0.07、0.118和0.14个旋回/m，根据频率倒数乘以采样频率可得旋回厚度(或周期时间)的公式，计算其对应的旋回厚度比为1∶0.3∶0.11∶0.086∶0.051∶0.043，这与6种天文周期的比值1∶0.3∶0.11∶0.088∶0.053∶0.044完全吻合.综上，通过对6个轨道周期的模拟与频谱分析，其结果不仅证明了FFT频谱分析米氏旋回的有效性与精确性，更为频谱分析识别划分地层旋回奠定了理论基础.

1.2 基于实际测井数据的米氏旋回频谱分析方法

基于米氏旋回的数值模拟与频谱分析结果，选择鄂尔多斯盆地三叠系长7段作为研究对象，以B159井长7段为例，该段厚度为124 m，是典型的陆相深湖—半深湖沉积，其构造稳定、连续性好，未发生沉积间断，且该段地层的岩性以泥页岩为主，而泥页岩中的黏土矿物对放射性元素吸附能力强，所以自然伽马曲线能够反映地层中黏土矿物含量的变化，从而敏感地识别沉积过程中受天文周期影响的米氏旋回(李凤杰等，2004；石巨业等，2017；Boulila et al.，2021).

选取B159井长7段的自然伽马曲线，采样间距Δ为0.125 m，提取该井段地层米氏旋回的频谱分析方法步骤为：(1)对GR数据进行lg(x+1)标准化预处理，再对预处理后的数据进行快速傅里叶变换，得到频谱图，如图2所示；(2)计算晚三叠世天文周期时间比为404 ka：123 ka：44.3 ka：35.4 ka：21.3 ka：17.8 ka，即天文周期比为1∶0.3：0.11∶0.088∶0.053∶0.044；(3)计算图2中有效频率所对应周期的比值，再与步骤(2)中的天文周期比作对比，结合图1模拟信号得出的6个米氏旋回对应的频率值，直接可找出与其相近的5个有效频率：0.00605、0.02015、0.0564、0.0705和0.1128个旋回/m，分别命名为A、B、C、D、E5个频率，且FFT频谱分析结果与MTM频谱分析结果一致；(4)通过周期旋回厚度或周期时间计算公式d=(1/f)×fs，计算得到A、B、C、D、E频率的旋回厚度分别为20.68 m、6.2 m、2.2 m、1.77 m和1.11 m，对应的旋回厚度比为1∶0.3∶0.11∶0.086∶0.054.其中，f为频率，fs为采样频率，值为8；(5)由于该段地层为深湖沉积环境、沉积稳定，其沉积物供给速率相对稳定，则识别出A频率的旋回厚度20.68 m对应为404 ka的长偏心率周期，B频率的旋回厚度6.2 m对应为123 ka的短偏心率周期，C频率的旋回厚度2.2 m对应为44.3 ka的地轴倾角长周期，D频率的旋回厚度1.77 m对应为35.4 ka的地轴倾角短周期，E频率的旋回厚度1.11 m对应为21.3 ka的长岁差周期；(6)根据上述米氏旋回的识别结果，即长7段包含的天文时间沉积周期，可用公式(2)计算出B159井长7段平均沉积速率为5.05 cm·ka-1.

×100=5.05 cm·ka-1,(2)

式中，Vp为频谱分析计算的平均沉积速率，dA、dB、dC、dD、dE分别为A、B、C、D、E频率的旋回厚度.

1.3 实际测井数据识别米氏旋回与计算沉积速率方法的应用效果分析

根据前文对B159井GR数据的频谱分析结果，分析该方法在识别米氏旋回与计算沉积速率的应用效果：(1)通过FFT频谱分析，可以将复杂的自然伽马数据变换到频率域，分析其频率信息，并提取能够反映米氏旋回周期的有效频率，从而更加有效地分析地层叠置旋回序列与时间周期；(2)根据FFT频谱分析及天文周期比识别出B159井长7段所包含的5个米氏旋回有效频率为0.00605、0.02015、0.0564、0.0705和0.1128个旋回/m(图2)；(3)计算5个有效频率对应的米氏旋回周期比为1∶0.3∶0.11∶0.086：0.054，其与天文周期比为1∶0.3∶0.11∶0.088∶0.053，非常接近，且误差不超过2.12%；(4)计算每个有效频率对应天文周期的旋回厚度分别为20.66 m、6.2 m、2.2 m、1.77 m和1.11 m，如表1所示，并可根据每个旋回厚度与旋回周期计算出每个天文周期的沉积速率，得出B159井长7段平均沉积速率Vp为5.05 cm·ka-1，这与Zhu等(2019)通过锆石U-Pb ID-TIMS测年获得长7段泥页岩沉积速率(5 cm·ka-1)非常吻合.

图2 Bai159井FFT频谱分析(a) 测井曲线； (b) GR的FFT分析结果； (c) GR的MTM分析结果.Fig.2 FFT spectrum analysis of Well Bai159(a) The logging curve; (b) The FFT analysis result of GR; (c) The MTM analysis result of GR.

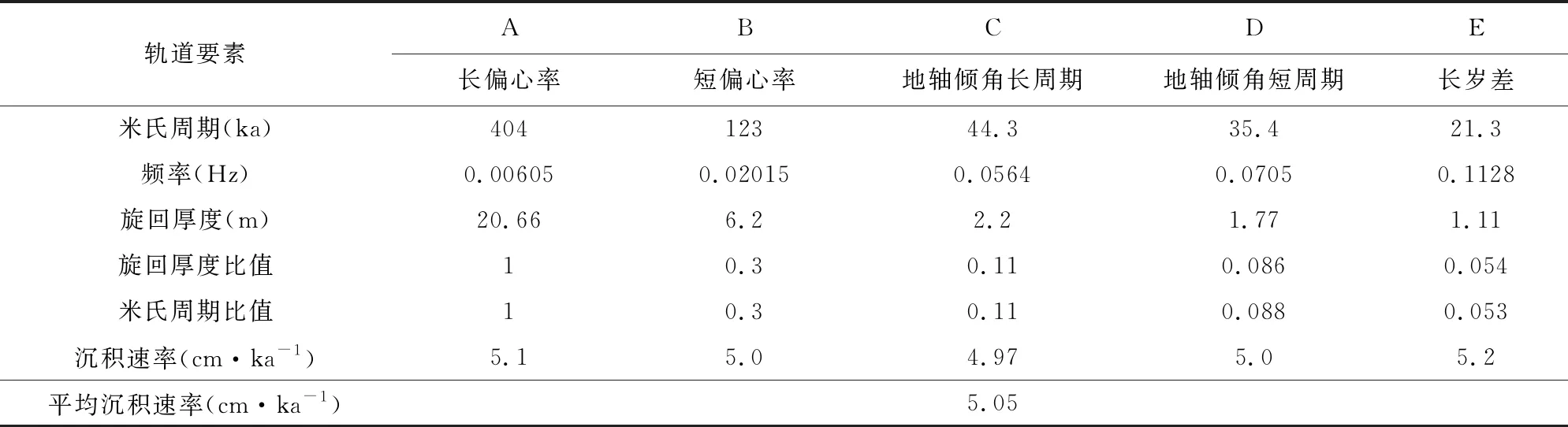
表1 鄂尔多斯盆地延长组长7段各天文周期的沉积速率计算结果Table 1 Calculation results of deposition rate in each astronomical period of Chang 7 Member of Yanchang Formation in Ordos Basin

2 米氏旋回小波深频分析方法

2.1 米氏旋回数值模拟与小波深频分析的理论基础

(3)

对测井信号做小波深频分析提取旋回信息的方法步骤如下：

(1)选取小波基函数，即母小波，一般选morlet小波，其不但具有非正交性而且还是由Gaussian指数复值小波，可以得到连续平滑的振幅和相位；

(2)选取一定尺度a的母小波与信号f(x)的起始点做卷积；

(3)计算得到小波变换后的系数CWTf(a,b)，它表示尺度a母小波与该段信号的相关程度.CWTf(a,b)越大，它们越相似；

(4)逐步按一定的步长向右平移小波进行计算，重复步骤(2)、(3)直到所有信号被覆盖，如图3所示，得到一组该尺度下的小波系数矩阵；

(5)然后，伸缩变换小波尺度因子a，重复步骤(2)—(4)；

(6)最后得到所有尺度a对应的小波系数CWTf(a,b)矩阵，即不同尺度(频率)的分频信息与能量旋回结构.

图3 小波深频分析变换步骤Fig.3 Wavelet deep-frequency analysis and transformation steps

从小波深频分析变换的步骤中可以看出，小波深频分析方法可以将一维深度域的测井数据转换为二维深度-尺度域的小波系数矩阵Ca×b.尺度a小波与信号的相似度越高，小波系数值越大，说明该深度位置很有可能存在尺度为a的沉积旋回.因此，可以通过小波系数值的大小变化，找出各种尺度的沉积旋回，再从中识别出尺度比(频率比)符合天文周期比的米氏旋回(徐敬领等，2009；张坦等，2017；闫建平等，2017).

为了论证小波深频分析识别米氏旋回的有效性，对米氏旋回做数值模拟研究：(1)模拟部分天文周期(长偏心率、短偏心率、短地轴倾角和短岁差周期)的单信号曲线，并将它们组合成一个复合信号(图4，第二—六列)，该复合信号则可代表周期性沉积叠置地层的测量信号；(2)对复合信号做小波变换，得到小波深频能量谱图(图4，最后一列)；(3)对不同尺度a的小波系数做模平均值，构建不同尺度a的小波系数模平均值曲线(图5).

图4 模拟的天文周期单信号、复合信号及小波深频分析能量谱图(a) 模拟的天文周期单信号与复合信号； (b) 复合信号的小波深频分析能量谱图.Fig.4 Simulated astronomical period single signal, composite signal and wavelet deep-frequency analysis energy spectrum(a) Simulated astronomical period single signal and composite signal; (b) The wavelet deep-frequency analysis energy spectrogram of the composite signal.

分析图4中模拟的复合信号曲线及小波深频分析结果可知：(1)6个天文周期组合的复合信号是比较复杂的，无法直观看出其包含的周期性信息；(2)小波深频能量谱图中(图4b)横坐标为尺度，从左到右尺度逐渐增大，小尺度代表了短周期沉积时间的地层叠置，即短周期沉积地层叠置序列，对应能量团个数较多，大尺度代表长周期沉积时间的地层叠置，即长周期沉积地层叠置序列，对应能量团个数较少；(3)小波深频能量谱图纵坐标指示了能量团代表的沉积地层叠置旋回边界位置及叠置旋回个数信息；(4)小波深频能量谱图(图4b)从左到右显示有4种尺度的能量团，分别对应4种天文周期的单信号信息，从左到右尺度逐渐增大，能量团也越大，每列能量团大小一样，对应尺度也一样.如短地轴倾角单频信号曲线的每个波峰和波谷对应着小波分析能量团(图4b)中从左数第二列每个能量团的中心，即波峰和波谷分别对应一个黄红色的能量团，因此两个相邻能量团中心的距离对应米氏周期的半旋回，3个能量团为米氏周期的一个完整周期旋回；(5)根据波峰、波谷与小波能量团的对应关系，对小波深频能量谱图中能量团的个数进行数数，小波深频能量谱图中共包含0.5个长偏心率周期的旋回，2.5个短偏心率周期的旋回，8.5个短地轴倾角周期的旋回，17.5个短斜率周期的旋回，与模拟的各天文周期旋回信号的个数是完全一致的，说明小波深频分析不仅可以识别不同级次(尺度)的周期叠置旋回，而且可以计算同一级次与不同级次(尺度)的周期旋回个数.

图5为小波系数模平均值曲线，主要是建立尺度与周期旋回级次的关系.图5中黑色圆圈为小波系数模平均值的局部极大值，其横坐标对应最优尺度为134、40和15，比值为1∶0.30∶0.11，与3种天文周期的比值1∶0.30∶0.11完全吻合，即对该模拟信号进行小波深频分析时，134尺度的小波系数或小波能量谱团对应长偏心率周期，40尺度的小波系数或小波能量谱团对应短偏心率周期，15尺度的小波系数或小波能量谱团对应长地轴倾角周期，可通过其中某个尺度的小波系数或小波能量谱团识别对应的地层周期叠置旋回.综上，通过对4个天文周期的模拟与小波深频分析，其结果不仅证明了小波深频分析米氏旋回的有效性与精确性，更为小波深频分析识别划分地层旋回奠定了理论基础.

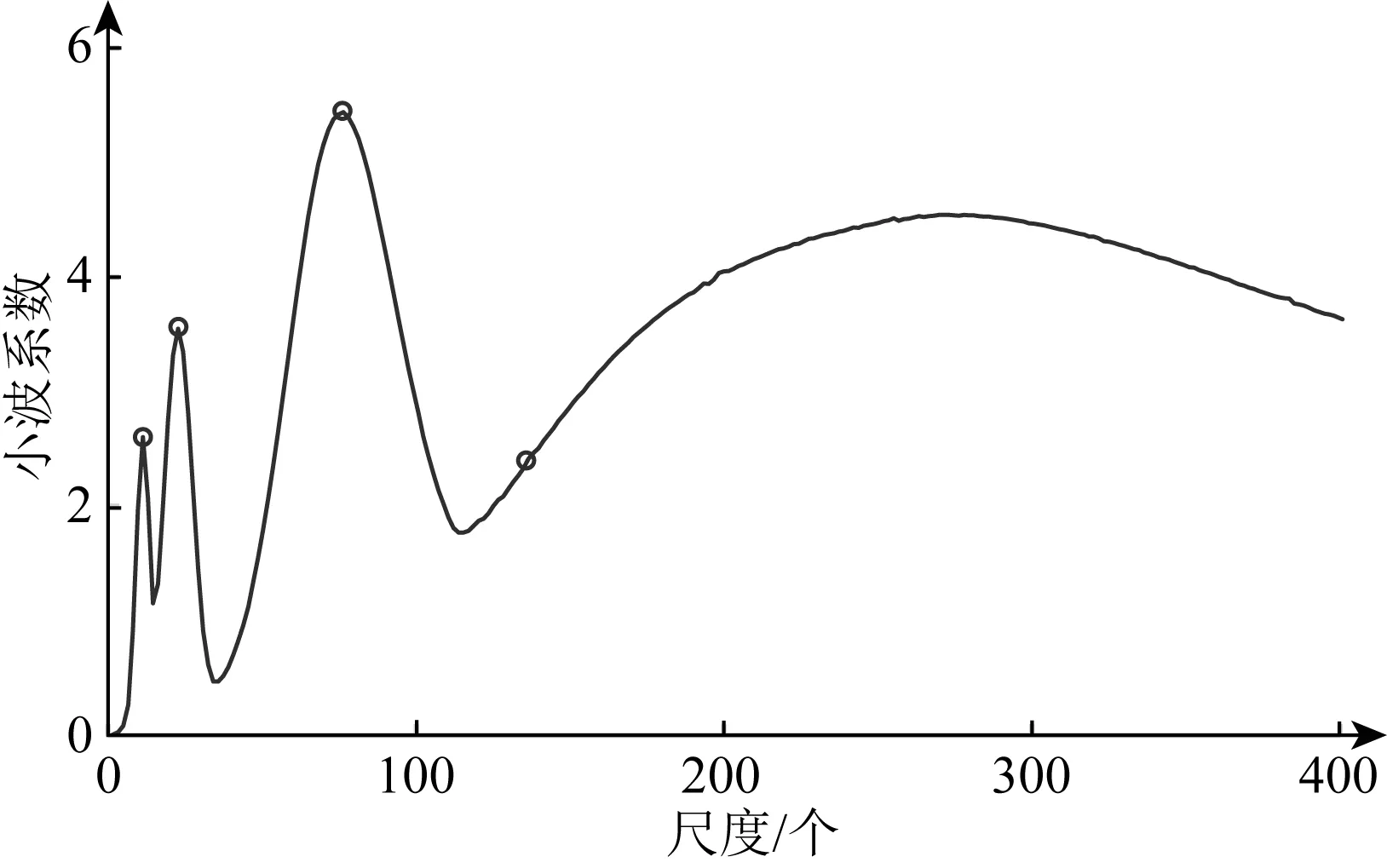
图5 复合信号小波分析的最优尺度选择(黑圈是局部极大值、为最优尺度的备选点)Fig.5 Optimal scale selection for wavelet analysis of composite signals (The black circles are local maxima, which can be used as candidate points for the optimal scale)

2.2 基于实际测井数据的米氏旋回小波深频分析方法

基于米氏旋回的数值模拟与小波深频分析结果，优选鄂尔多斯盆地三叠系长7段作为研究对象，并取B159井长7段的自然伽马曲线作为分析数据，采样间隔Δ为0.125 m，提取该井段地层米氏旋回的小波分析方法步骤为：(1)根据B159井的分层数据，选用B159井长7段的GR数据，如图6第二列所示；(2)对该段GR数据进行lg(x+1)标准化预处理，然后选取Morlet小波(中心频率Fc=0.8125)作为小波基函数进行小波深频分析，得到小波深频能量谱图，并做了镜像处理，如图6第三列(图6b)，横坐标为尺度；(3)计算每个尺度下小波系数的模平均值，构建不同尺度的小波系数模平均值曲线，如图6第四列(图6c)，局部极大值处为最优尺度；(4)根据频谱分析法计算的长7段平均沉积速率Vp=5.05 cm·ka-1，以及公式(4)、(5)、(6)得到尺度a=(Fc×Vp×T)/(100×Δ)，将6种天文周期T的值代入即可计算相应尺度值，根据计算结果推测各个天文周期对应的最大尺度值不超过134；(5)根据图6c小波系数模平均值曲线得到大小不超过134的四个最优尺度：12、15、40和134，再参考小波能量谱图筛选出符合天文周期比的尺度134、40，其比值为1∶0.3，因此推断尺度134和40分别对应长偏心率和短偏心率周期；(6)通过尺度值即可根据式(4)、(5)、(6)计算相应天文周期的频率、沉积厚度及沉积速率:

图6 B159井长7段GR曲线及其小波深频分析结果(a) B159井长7段GR曲线; (b) GR的小波深频分析能量谱图; (c) GR的小波分析最优尺度.Fig.6 GR curve and wavelet deep-frequency analysis results of Chang 7 Member of Well B159(a) GR curve of Chang 7 Member of Well B159; (b) The middle picture is the energy spectrum of GR wavelet deep-frequency analysis; (c) The optimal scale of GR wavelet analysis.

(4)

(5)

(6)

其中，f为该尺度下天文周期的频率，个旋回/m；d为该尺度天文周期内的地层沉积厚度，m；v为该尺度天文周期内地层的沉积速率， cm·ka-1；T为沉积时间，ka.

最后，根据公式(4)和(5)得到该尺度天文周期内地层沉积厚度：d=(a×Δ)/Fc，计算出长偏心率和短偏心率周期的沉积厚度分别为20.62 m和6.2 m；(8)根据计算的沉积厚度及长偏心率和短偏心率的周期，可用公式(6)计算出B159井长7段平均沉积速率为5.07 cm·ka-1:

(7)

式中，Vp为小波深度分析计算的平均沉积速率，dA、dB分别为长偏心率和短偏心率周期的沉积厚度.

2.3 实际测井数据识别米氏旋回与沉积速率的应用效果分析

根据图6 B159井GR数据的小波深频分析结果，分析该方法在识别米氏旋回与计算沉积速率的应用效果：(1)通过小波分析，可以将复杂的自然伽马数据变换到二维深度-尺度域的小波系数矩阵；(2)根据小波分析能够识别出地层中的优势旋回，即包含米氏周期的旋回，并能提供这些优势旋回随深度的变化信息及对应尺度；(3)根据小波深频分析能量谱图及天文周期比识别出B159井长7段所包含的2个米氏旋回最优尺度为134和40；(4)计算2个最优尺度对应的米氏旋回周期比为1∶0.2985，其与天文周期比1∶0.3非常接近，且误差不超过0.5%，即可推断出2个最优尺度的米氏旋回分别对应长、短偏心率；(5)识别出B159井长7段含有6个长偏心率旋回，20个短偏心率旋回，且尺度为134的1个长偏心率旋回约包含尺度为40的3个短偏心率旋回；(6)小波深频分析能量谱图中，尺度等于134的能量谱团旋回厚度与计算的长偏心率周期沉积厚度一致，尺度等于40的能量谱团旋回厚度与计算的短偏心率周期沉积厚度也一致.如图6，在2010～2030.6 m深度段，尺度为134的能量谱团指示了该段含有1个长偏心率旋回，则一个长偏心率旋回的厚度约为20.6 m，与前文公式(5)、(6)计算的长偏心率周期沉积厚度20.62 m吻合；(7)最后根据旋回周期与旋回厚度，计算B159井长7段平均沉积速率Vp为5.07 cm·ka-1，这与频谱分析法计算的平均沉积速率Vp(5.05 cm·ka-1)比较相近，且与Zhu等(2019)通过锆石U-Pb ID-TIMS测年获得长7段泥页岩沉积速率(5 cm·ka-1)非常吻合.

3 浮动天文年代标尺的建立

为了研究地层沉积、地质事件的持续时间，以及古气候、古环境与地质事件的关系，需要建立高精度且具有相对时间概念的浮动天文年代标尺(吴怀春等，2011).由于三叠纪时期火星和地球轨道的谐振作用发生了变化，导致短偏心率周期产生一定的改变，而长偏心率周期在该地质历史时期则具有较强的稳定性(Laskar，2004).因此，研究对象为鄂尔多斯盆地三叠系长7段时，以长偏心率周期为主、以其它天文周期为辅来重构各尺度下的测井曲线，作为建立浮动天文年代标尺的依据.

三叠纪长7段浮动天文年代标尺建立过程为：(1)根据B159井长7段的小波分析结果，得到反映米氏旋回周期的最优尺度为134和40，分别对应长偏心率周期和短偏心率周期；(2)提取出尺度134和40对应的小波系数，小波系数随深度的变化曲线即为该尺度下的重构测井曲线，曲线中两个相邻极大值点的距离表示该尺度旋回的一个周期；(3)编写算法剔除重构曲线中具有干扰性的无效极大值点，仅标记有效极大值点并计算旋回的个数，如图7所示.

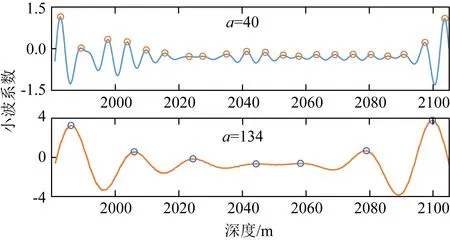
图7 小波深频分析重构米氏旋回曲线(红圈为有效极大值点，两个相邻红圈间距为一个周期)Fig.7 Reconstructed Milankovitch cycle curves of wavelet deep-frequency analysis (The red circle is the effective maximum point, and the distance between two adjacent red circles is one period)

(4)Zhu等(2019)采用锆石U-Pb ID-TIMS测年技术获得长7段顶部烃源岩年龄约241.558 Ma，根据测得顶部岩石年龄和尺度134的长偏心率重构曲线得到的该地层沉积时间，可得出地层的时间序列，即地质历史时间，如图8第八列所示；(5)以尺度134的长偏心率重构曲线为依据，绘制长偏心率周期旋回的地层厚度及沉积速率随时间的变化曲线，如图8最后一列，图中曲线上标注的数字为深度点，两个深度点的距离为一个长偏心率周期时间，曲线斜率为沉积速率；(6)综合测井曲线、小波深频色谱图(图8第五列)、不同尺度对应的重构曲线(图8第六/七列)、地层历史时间(图8第八列)、旋回地层厚度及沉积速率变化(图8第九列)，得出综合分析图.综上，通过小波深频分析，从B159井长7段GR数据中提取出404 ka的长偏心率周期和123 ka的短偏心率周期两条曲线，将这两条曲线作为调谐曲线建立了长7段的浮动天文年代标尺.

图8 B159井长7段浮动天文年代标尺第五列为小波深频分析能量谱图;第六列为重构的143尺度对应长偏心率周期曲线；第七列为重构的40尺度对应短偏心率周期曲线；第八列为确定的年代；第九列黑色横杠为长偏心率旋回地层的深度点与年代点，红色斜线为沉积速率曲线，斜率越大、沉积速率越大.Fig.8 Floating astronomical data scale of Chang 7 member of Well B159The fifth column is the wavelet deep frequency analysis energy spectrum; The sixth column is the reconstructed 143-scale long eccentricity period curve; The seventh column is the reconstructed 40-scale short eccentricity period curve; The 8th column is the determined age; The black horizontal bar in the ninth column is the depth point and age point of the formation with long eccentricity period, and the red oblique line is the deposition rate curve, the greater the slope, the greater the deposition rate.

根据图8各列信息的对比，分析该方法在建立浮动天文年代标尺的应用效果：(1)404 ka长偏心率曲线和123 ka短偏心率曲线的波峰与波谷位置都与小波深频色谱图中的能量团有着很好的对应；(2)研究出尺度与典型米氏周期(长偏心率、短偏心率)的关系，即尺度134和40分别对应长、短偏心率，根据关系与小波系数，计算出B159井长7段共记录了6个长偏心率旋回，20个短偏心率旋回；(3)鄂尔多斯盆地三叠系长7段长偏心率比较稳定(Laskar，2004)，以404 ka长偏心率曲线为基准，计算出B159井长7段的沉积时限约为6×404 ka=2424 ka，平均沉积速率V=124 m/2424 ka=5.1 cm·ka-1，这与频谱分析、小波分析计算结果十分吻合，并与Zhu等(2019)前人计算结果也完全吻合，论证了以长偏心率曲线精细标定地层相对时间的可靠性；(4)长7段地层短偏心率周期虽然有不断变化，但长偏心率周期与短偏心率周期的旋回个数比为20∶6=1∶0.3，与天文周期比完全吻合，说明短偏心率仍能够作为精细标定长7段地层相对时间的参考依据；(5)图8最后一列黑色横杠除了代表深度点，同时也表示了叠置层的沉积时间点，其长短代表了地层的相对历史时间，其长度越短表示地层历史时间相对越新，深度由深到浅对应地层时间由老到新，相邻黑色横杠的垂直距离为旋回的沉积厚度，因此红色线条的斜率越大，相应层段的沉积速率越大；(6)将第二—四列测井曲线与最后一列沉积速率作对比，发现沉积速率低的旋回地层，对应测井响应特征为泥岩的地层，沉积速率高的旋回地层，对应测井响应特征为砂岩的地层，即泥岩层的沉积速率小，砂岩层的沉积速率相对大.

4 结论

(1)基于频谱分析与小波深频分析的理论研究，通过对米氏周期进行数值模拟并进行频谱分析与小波深频分析，论证出两种方法均可识别信号中的周期性信息，即可提取地层周期性、旋回性信息，特别是米氏旋回，用于沉积时间与沉积速率的研究；小波深频分析还直观体现出能量谱团的变化、叠置旋回的个数及边界，但由于沉积地层存在多变性，两种分析方法结合起来使用效果更好，相互印证.

(2)建立了频谱分析与小波深频分析米氏旋回、沉积时间及速率的方法步骤与公式，并对鄂尔多斯盆地B159井长7段自然伽马数据分别做频谱分析和小波深频分析，识别出沉积厚度符合天文周期比的米氏旋回，表明长7段沉积过程受到天文周期的影响，广泛保存了米氏旋回.

(3)采用频谱分析和小波深频分析方法分别计算出鄂尔多斯盆地B159井长7段的平均沉积速率为5.05 cm·ka-1和5.07 cm·ka-1，与前人研究结果吻合.

(4)鄂尔多斯盆地长7段地层旋回主要受404 ka的长偏心率周期控制，该地层共识别出6个长偏心率旋回和20个短偏心率旋回，计算出长7段124 m地层沉积时限约为2.4 Ma.

(5)形成了天文年代标尺的计算方法步骤，并建立了鄂尔多斯盆地长7段浮动天文年代标尺，有助于对地质事件的持续时间做出精确的估计.