基于多层感知机重建GRACE与GRACE-FO之间数据缺失的黄河流域陆地水储量变化

石通， 刘新*， 穆大鹏， 李成名， 郭金运*， 邢云鹏

1 山东科技大学测绘与空间信息学院， 山东青岛 266590 2 山东大学空间科学研究院， 山东威海 264209 3 中国测绘科学研究院， 北京 100036

0 引言

GRACE重力卫星计划由美国宇航局(NASA)和德国空间飞行中心(DLR)联合开发，于2002年3月成功发射，可以探测到地球重力场的时变特征，时间分辨率为10天至30天(Tapley et al.，2004).GRACE时变重力数据被广泛应用于地球表面质量变化的研究，为陆地水储量变化的反演提供了一种新的手段.目前，国内外已经有很多学者将GRACE重力卫星应用到如流域、区域陆地水储量观测(Chen et al.，2014, 2017；Guo et al.，2014，2016； Liu et al.，2020a)、冰川和两极质量的动态监测(Luthcke et al.，2013；Velicogna and Wahr，2013；高春春等，2019)、洪涝干旱灾害的监测(Long et al.，2014)、全球海平面变化(Jacob et al.，2012)等领域.这些研究表明，GRACE重力卫星的观测结果可以作为传统地表水文观测技术及重力观测的有效补充，在近年来的水文学和地学研究中得到越来越广泛的应用.

经过长达15年之久的运行，GRACE卫星于2017年6月退役，GRACE Follow-On(GRACE-FO)重力卫星于2018年5月22日发射，两颗重力卫星之间存在接近一年的间断期.Velicogna等(2020)分析了格陵兰岛和南极洲的GRACE与GRACE-FO任务之间的数据连续性，发现在大陆和区域尺度上二者数据有较好的一致性.虽然现有的GRACE数据已经能够实现监测陆地水储量变化，但是为了研究陆地水储量长期变化，需要更长时间的数据积累.已有学者提出了对GRACE数据的重建方法以及间断期的连接方法，如自回归模型(Forootan et al.，2014)、线性回归模型(Nie et al.，2016)、统计公式模型(Humphrey and Gudmundsson，2019)、奇异谱分析法(Li et al.，2019)、深度机器学习法(Sun et al.，2020；Li et al.，2021).

当前黄河流域生态环境脆弱，水资源保障形势严峻，全球变暖背景下的气候变化和人类活动使黄河流域的水循环发生显著变化，对黄河流域水资源造成影响.已有学者针对黄河流域研究水储量变化(尼胜楠等，2014；Jing et al.，2019；Liu et al.，2020b；张璐等，2020)，但其研究时段均较短，且未使用GRACE-FO卫星观测数据.

本文基于多层感知机(Multi-Layer Perceptron, MLP)神经网络模型，结合GLDAS、CPC水文模型、降水、蒸散量以及土壤温度数据，以黄河流域为研究区，重建GRACE与GRACE-FO之间缺失等效水高，重点分析黄河流域上中下游陆地水储量变化与降水、蒸散发及土壤温度的关系，并使用连续小波分析和交叉小波分析研究GRACE反演的陆地水储量与GLDAS、CPC结果的周期特征.

1 研究区域与数据

1.1 研究区概况

黄河流域位于东经96°—119°、北纬32°—42°之间，流域面积79.5万km2.河口镇以上为黄河上游，河道长3472 km，流域面积42.8万km2；河口镇至桃花峪为中游，河道长1206 km，流域面积34.4万km2；桃花峪以下为下游，河道长786 km，流域面积只有2.3万km2.黄河流域年降水量在100～1000 mm之间，中上游南部和下游地区降水大于650 mm，而在内陆的西北宁夏、内蒙古部分地区，年降水量不足150 mm，在秦岭山脉北坡，由于受地形影响较大，降水多在700～1000 mm.流域整体春冬少雨干旱，秋夏雨量充足.图1为黄河流域上中下游位置示意图.

图1 黄河流域位置Fig.1 Location of Yellow River basin

1.2 数据

1.2.1 时变重力场数据

GRACE及GRACE-FO月时变重力场模型的处理与发布主要由美国德克萨斯大学空间研究中心(CSR)、德国地学研究中心(GFZ)和美国喷气动力实验室(JPL)三个研究中心提供.本文采用CSR、JPL、GFZ提供的2002-04—2020-12共192个月(缺失2017-07—2018-05及部分月份)的GRACE level-2 RL06 GSM 60阶月时变重力场模型，分别记为CSR-SH、JPL-SH、GFZ-SH.对于GRACE及GRACE-FO在其单独任务期间的1个月或2个月缺失通过相邻月份的平均值进行线性插值弥补(Long et al.，2015).

本文还采用了CSR、JPL发布的Mascon格网数据(Watkins et al.，2015；Save et al.，2016)，以下分别记为CSR-M与JPL-M.CSR-M与JPL-M格网大小分别为0.25°×0.25°与0.5°×0.5°.

1.2.2 水文模型

GLDAS水文模型与由GRACE反演的水储量之间有很强的相关性(Long et al.，2013)，本文选取GLDAS-Noah水文模型(Rodell et al.，2004)，数据的时间跨度为2002-04—2020-12共225个月，时间分辨率为1月，格网大小为0.25°×0.25°.该水文模型是由美国宇航局戈达德空间飞行中心(GSFC)和美国国家环境预报中心(NCEP)联合建立的全球水文模型，反映了陆地表面土壤水、冰和雪的变化.在GLDAS水文模型中提取0～2 m土壤湿度、积雪融水以及植被冠层水作为陆地水储量.另外在GLDAS水文模型中提取土壤温度和蒸散量，这两个变量与陆地水储量变化有一定的联系(Li et al.，2021).

CPC水文模型(Fan and van den Dool，2004)全球土壤湿度也用于估计与气候相关的水储量变化(李圳等，2018； Zhong et al.，2019)，CPC水文模型由美国国家海洋和大气管理局(NOAA)发布.选用该数据的时间跨度与GLDAS相同，格网大小为0.5°×0.5°，从CPC水文模型中提取0～1.6 m土壤湿度，并且包括了积雪融水等引起水平衡变化的因素.

1.2.3 降水数据

本文采用中国地面降水月值0.5°×0.5°格点数据集(V2.0)(赵煜飞等，2014)，该数据由中国气象网提供的2472个地面雨量站点进行空间插值得到.台站在中国东部地区密集且分布均匀，西北和东北地区相对稀疏.

数据来源信息如表1所示.

表1 数据来源信息Table 1 Data source information

2 方法

2.1 GRACE时变重力场数据处理

在GRACE数据后处理过程中，由于GRACE卫星的参考框架原点为地球质心，其时变重力场模型不包含一阶项系数，为此需要使用SLR观测的一阶项来替换，从而顾及地心运动的影响(Swenson et al.，2008; Sun et al.，2016；孙玉等，2019)，同时GRACE对时变重力场的C20项也不敏感，此外从2016年10月开始，GRACE卫星上一个加速度计出现故障，造成C30项精度较低(Loomis et al.，2020)，因此使用JPL及NASA GSFC发布的TN-13和TN-14数据分别替换一阶项、C20与C30项.为了消除平均地球重力场的影响，将月时变重力场球谐系数减去其2004—2009年平均值，进行与Mascon相同的去平均方法，以研究时变重力场的特点.尽管RL06月重力场模型(Dahle et al.，2019)条带误差及高频噪声减小了很多，但剩余的误差依然不可忽视.因此本文采用DDK3去相关滤波(Horvath et al.，2018)的方法对球谐系数进行处理.等效水高(Equivalent Water Height，EWH)(Wahr et al.，1998)为：

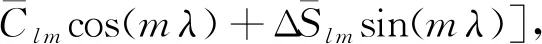
为了与GRACE数据进行对比，需要把GLDAS、CPC水文模型计算的陆地水储量进行球谐展开到60阶次，并进行300 km高斯滤波处理.

2.2 多层感知机重建等效水高

MLP是一种典型的前馈人工神经网络，适合对大量数据进行分类、建立复杂的非线性映射等问题.在设法获得有限的输入变量与相应的输出变量后，即可利用MLP网络来模拟输入与输出之间的联系，从而建立基于 MLP模型的预测方法(Pal and Mitra，1992；Kuremoto et al.，2014).由于本研究的重建方案是将若干输入变量映射到输出变量的回归问题，所以使用MLP神经网络模型.

如图2所示，MLP模型是由多层密集连接的信息处理节点所形成的网络(Zhu et al.，2021)，这些信息处理节点称为神经元.MLP网络由一个输入层、一个或多个隐含层和一个输出层组成.输入层是用于输入数据的节点，其数量与数据变量的个数一致，隐含层和输出层分别由神经元和输出变量组成.相邻层之间为全连接，而同一层的节点间未连接.本研究中使用三个隐含层，分别有512、256、128个神经元.将时间、经纬度、GLDAS水储量、土壤温度、蒸散量、降水量以及CPC水储量当作神经网络输入参数，输出参数为GRACE等效水高.

MLP神经网络信息处理机制(Zhu et al.，2021)为：

y=f(Wx+b),(2)

其中，x是神经元的输入，W和b分别代表连接权值和偏置，f(·)为神经元的激活函数，选择tanh函数，以捕捉输入信息的非线性信息.由于在本研究中MLP网络被应用到一个回归问题并且输出是任意的，因此不应在最后一个隐含层中使用激活函数，所以输出层的输出机制为：

y=Wx+b.

(3)

通过神经元对信息的处理及层层传递，MLP模型完成了从输入到输出的映射.MLP模型学习的本质就是通过网络的信息前向传递及误差逆向传播实现梯度下降算法，不断调整网络权值矩阵W和偏置矩阵b，使得网络理想输出与实际输出的误差达到最小.

在向MLP神经网络模型输入参数之前，需要把数据进行标准化，即：

图2 MLP网络结构，输入层参数分别为时间、经度、纬度、GLDAS与CPC水储量、降水、蒸散发(ET)及土壤温度(SoilTMP)，输出参数为GRACE等效水高Fig.2 Structure of MLP network. The input layer parameters are time, longitude, latitude, GLDAS TWS (terrestrial water storage), CPC TWS, precipitation, evapotranspiration (ET) and soil temperature (SoilTMP),the output parameter is GRACE EWH

(4)

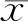
在月时间尺度上，由式(1)计算的等效水高与MLP网络得到的等效水高重建精度评价选用皮尔逊相关系数r(式(5))、纳什系数Ens(式(6))、平均绝对误差MAE(式(7))与均方根误差RMSE(式(8))：

(5)

(6)

(7)

(8)

相关系数r的取值范围为|r|≤1，|r|越接近于1，则表明等效水高与其重建值相关程度越高.纳什系数Ens反映拟合程度，Ens取值范围为负无穷至1，Ens越接近1，表示重建质量好，模型可信度高.MAE与RMSE越小，重建精度越高.

3 结果与分析

3.1 MLP神经网络重建结果验证

对于已有GRACE及GRACE-FO的时变重力场数据，从2004—2015年逐次空缺一年进行实验，以验证等效水高重建精度.本文使用MLP神经网络的目的是重建GRACE与GRACE-FO两代重力卫星之间缺失的约一年数据，所以选择缺失一年作为验证，若扣除过多的年份则MLP神经网络学习的样本数据减少，且与真实缺失时间差异较大.基于MLP神经网络模型训练时间为GRACE运行时间(2002-04—2017-06)和GRACE-FO运行时间(2018-06—2020-12)，在训练时间中从2004—2015年逐年地扣除一年，共构成12次实验，模型具体训练时间如表2所示.

表2 MLP网络训练时间Table 2 Training time of MLP network

模型训练后，再输入空缺年份的土壤水含量、降水、蒸散发及土壤温度等数据，用MLP模型重建出此缺失时段的GRACE EWH.利用训练样本对MLP网络进行训练，网络的参数根据误差梯度不断修正，输出结果逐步逼近训练集的输出结果.图3给出了黄河流域EWH与对应重建值，图3中数字对应实验序号.由图3可以看出在逐年空缺的实验中，等效水高重建值与真实值相符程度较高，相关系数r均大于0.93(p<0.01).但重建值在其拐点处与真实值有着一定的差距，而在拐点之间重建效果较好，其原因为极值点之间的数据多，MLP网络训练程度高，而极值处的等效水高数据少，MLP网络对极值不敏感，导致拐点处的重建效果差一些.

图3 黄河流域等效水高重建Fig.3 Reconstructed EWH in the Yellow River basin

图4给出了12次实验重建等效水高与真实值之间各检验参数的平均值在空间上的分布.各格网点等效水高真实值与重建值的相关系数r均大于0.5(p<0.01)，且有97%以上的相关系数r大于0.8(p<0.01)，表明MLP网络重建值与数据真实值之间的相关性较强.有82%以上Ens值大于0.5，表明MLP模型重建值的拟合程度高.至于(100°E，38°N)附近拟合程度较差，其原因为边界效应的影响，MLP模型训练该区域附近的格网点较少，导致其重建精度较差.MAE与RMSE最大值分别为1.52 cm和2.04 cm，误差较大处均位于流域边界处，原因也由于MLP网络没有训练黄河流域边界之外的格网点数据，导致临近边界处误差大，而流域内部的MAE与RMSE均较小，满足重建精度要求.以上实验证明了MLP网络对于重建GRACE与GRACE-FO两代重力卫星之间缺失等效水高数据的可行性.

图4 黄河流域等效水高重建值与真实值的误差检验Fig.4 Accuracy of the reconstructed and true EWH in the Yellow River basin

基于上述实验，保持输入参数不变，模型训练时间为2002-04—2017-06和2018-06—2020-12，将EWHMean-SH、EWHCSR-SH、EWHJPL-SH、EWHGFZ-SH、EWHCSR-M、EWHJPL-M逐一作为输出参数进行多次实验.模型训练后，输入2017-07—2018-05的各输入参数，MLP网络将重建出该时间段的黄河流域各格网点等效水高值.图5a给出了2002—2020年黄河流域等效水高，图5b为MLP网络重建的黄河流域在2017—2018年等效水高值.由于不同机构对于GRACE观测数据的处理方式不尽相同，导致计算的EWH值也有一定差异，造成MLP网络建立的模型差异，但也可在预测期间体现出等效水高大致变化情况.EWHMean-SH与EWHCSR-M的RMSE为0.88 cm，GRACE 球谐系数反演结果与Mascon数据吻合程度较好，说明使用Mean-SH计算的EWH可信度较高，且避免了某些月份的异常值，所以在下文讨论黄河流域水储量变化时均使用EWHMean-SH.

3.2 GRACE与水文模型时间序列分析

GRACE反演的黄河流域EWHMean-SH与GLDAS、CPC水文模型得到的水储量变化时间序列见图6.图6水储量时间序列结果均表现出明显的季节性，分别在秋季和春季达到最大值和最小值.对于图6a黄河流域整体来说，GRACE数据反演的EWH在2015年之前与水文模型结果符合程度较高，GRACE与GLDAS相关系数r为0.69(p<0.01)，而在2015年以后二者相关系数r为0.37(p<0.01).在2015年之后，GLDAS得到的水储量变化均高于GRACE数据反演的EWH，且GRACE反演的水储量呈现明显的下降趋势，而水文模型得到的水储量历年结果大致持平甚至略微上升，具体原因可能为GRACE重力卫星与水文模型监测的具体内容有所不同.GRACE反演结果包含多种因素，而GLDAS数据仅包含土壤水、积雪融水及植物冠层水含量，不包含深层水的变化，GLDAS、CPC水文模型仅能探测到浅层地表水，而黄河流域用水量大，对地下水超采严重，导致深层水储量逐年减少，这部分能够被GRACE重力卫星探测到(冯伟等，2012).基于2004—2009年距平值，黄河流域EWH变化范围为-10.8～7.9 cm.

由图6b、c可知黄河流域上游与中游地区水储量情况相似，在研究期间大致呈现持平趋势，且上游与中游地区GRACE反演的EWH与水文模型相关性较好，上游与中游的GRACE与GLDAS相关系数r分别达到0.6与0.38(p<0.01)，进一步验证了GRACE反演结果的可靠性.而黄河流域下游地区由GRACE反演的EWH呈现明显的下降趋势(见图6d)，且年内变化规律性较差，波动较多，GRACE与水文模型相关性均较小，而GLDAS与CPC相关系数r达到0.8(p<0.01)，说明下游地区GRACE探测到深层地下水亏损严重，人为因素影响大.

对于黄河流域整体及上中下游2002—2020年EWHMean-SH及GLDAS、CPC水文模型得到的水储量时间序列按照(9)式(尼胜楠等，2014)进行最小二乘拟合，以研究水储量在季节尺度上速率、振幅及相位的变化情况：

(9)

其中，Ai为振幅，φi为相位，Ti为周期，考虑周年及半年变化项，取a1作为EWH年变化速率.

由表3可见，由GRACE反演的黄河流域水储量呈现以-0.51±0.03 cm·a-1的速率减少，而GLDAS及CPC水文模型变化速率大致相当，均为略微上升，GRACE反演结果与水文模型差距较大的原因为黄河流域地表土壤水保持情况较好，而深层地下水逐年减少，尤其以下游地区最为明显.GRACE和GLDAS、CPC水文模型的周年相位较为一致，与GLDAS的周年振幅也较接近，而CPC的振幅明显高于其他两者，由于不同水文模型融合了不同的数据源，其包含的信息与精度存在一定的差异(李圳等，2018)，造成CPC水文模型的年周期振幅较大.

表3 黄河流域陆地水储量变化速率、振幅及相位Table 3 Rate, amplitude and phase of EWH in the Yellow River basin

为研究黄河流域水储量年际变化特征，采用13点滑动平均(13 points moving average，13PMA)(李武东等，2017)的方法来体现周年波动，结果见图7.由图7a可知，黄河流域水储量整体上呈现下降趋势，2003—2004年水储量呈现明显的上升趋势后，在2004年春季达到最大值，此后直到2017年均大致呈现出不同程度的下降，于2017年后又呈现出上升趋势.GLDAS与CPC水文模型结果显示浅层水储量大致呈现持平或上升趋势.由图7b、c可以看出黄河流域上游与中游水储量在2002—2015年间变化不大，而2015—2016年间呈现出明显下降趋势，又在此后呈剧烈上升.而图7d表明黄河流域下游地区在研究期间均呈现不同程度的下降趋势，仅在2012年及2020年出现明显上升趋势.

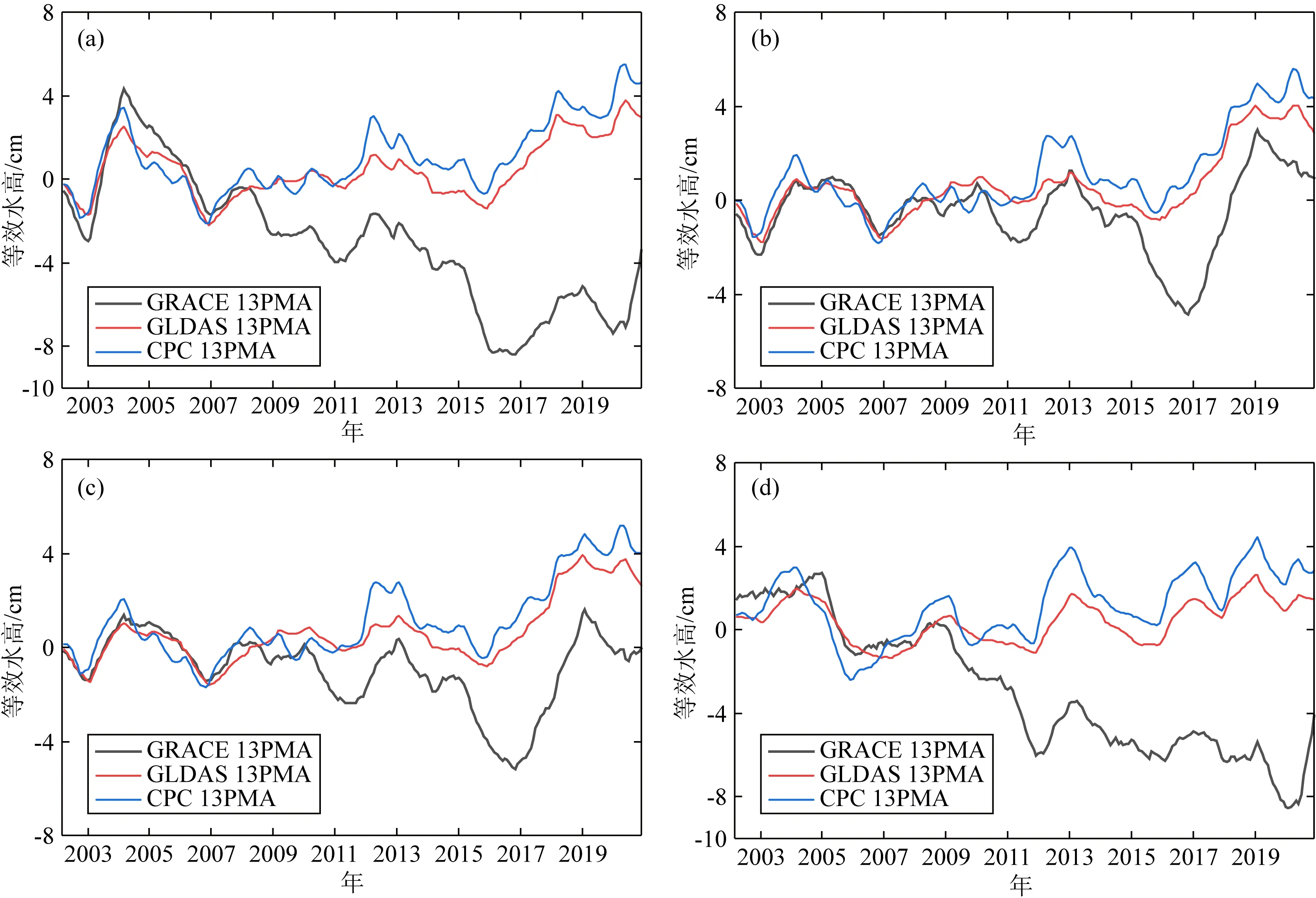
图7 采用13点滑动平均方法得到的等效水高年际变化趋势(a) 黄河流域整体； (b) 黄河流域上游； (c) 黄河流域中游； (d) 黄河流域下游.Fig.7 EWH interannual trends using 13 points moving average method(a) Overall Yellow River basin； (b) The upper reach of Yellow River basin； (c) The middle reach of Yellow River basin；(d) The lower reach of Yellow River basin.

3.3 黄河流域陆地水储量空间变化趋势

为研究黄河流域在2002年至2020年陆地水储量变化情况，利用GRACE球谐系数及Mascon计算了黄河流域水储量年际变化趋势.如图8所示，黄河流域EWH变化趋势上中下游差异明显，其中上游水储量保护情况较好，呈现略微上升趋势，由图8a—d可以看出球谐系数反演的结果对上游增长趋势较为敏感；中游大致呈现持平或略微下降趋势；而下游华北平原呈现严重亏损趋势，以图8e、f中Mascon对下游地区水储量严重亏损的反映最为明显.JPL-M格网大小虽然为0.5°×0.5°，但其许多相邻格网的数值一致，导致图8f中出现较大面积的相同数据.

图8 GRACE反演黄河流域等效水高变化率Fig.8 Rates of EWH from GRACE in the Yellow River basin

4 讨论

4.1 黄河流域EWH影响因素分析

在流域水文循环过程中，陆地水储量能够综合反映循环过程中降水、蒸散发等各种水文过程，其中降水能够导致流域水储量增加，而蒸散发等水文过程会使水储量减少，土壤温度的变化直接影响着蒸散发，进一步影响水文循环.水储量变化与降水、蒸散发及径流的关系(尼胜楠等，2014)为：

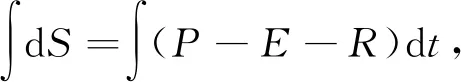
(10)

其中S为水储量，P为降水，E为蒸散发，R为径流.

本节主要分析降水、蒸散及土壤温度对黄河流域EWH的影响，并将EWH分别与降水量、蒸散量以及土壤温度进行对比分析，如图9所示，图中降水量、蒸散量以及土壤温度均已去除了2004—2009年的平均值，即距平值.

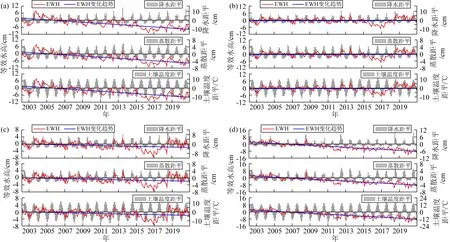
图9 GRACE反演黄河流域EWH与降水、蒸散发及土壤温度时间序列对比(a) 黄河流域整体； (b) 黄河流域上游； (c) 黄河流域中游； (d) 黄河流域下游.Fig.9 Time series of EWH by GRACE compared with precipitation, evapotranspiration and soil temperature in Yellow River basin(a) Overall Yellow River basin； (b) The upper reach of Yellow River basin； (c) The middle reach of Yellow River basin；(d) The lower reach of Yellow River basin.

对黄河流域整体及上中下游在研究期间由GRACE反演的水储量变化与降水、蒸散量以及土壤温度的相关系数以及滞后性进行分析，取最大滞后相关系数对应的时间作为滞后时间，结果见表4.

表4 黄河流域EWH与降水、蒸散发及土壤温度的滞后时间及相关系数Table 4 The lag time and coherence of the EWH with precipitation, evapotranspiration and soil temperature in Yellow River basin

4.1.1 降水对EWH的影响

降水是黄河流域水文循环过程中主要的水量来源，在水文循环过程中发挥着重要作用.黄河流域降水主要集中在汛期(6—10月)，汛期降水量占全年的70%以上，而冬季降水量仅占全年的2%～3.7%.由图9可知黄河流域水储量与月降水量呈现相同的季节性变化趋势，在降水汛期水储量显著上升.水储量在2003—2004年呈现上升趋势，上升速率高达4.21±1.3 cm·a-1，这与2003年黄河流域降水量均较常年偏多，且出现了多年不遇的秋汛密切相关，导致黄河流域的水储量距平值在2003年11月达到了研究期间的最大值+7.9 cm，并从此后2004年开始水储量距平值呈现逐年减少趋势，在2015—2016年间黄河流域EWH出现了明显下降，速率达-2.52±0.65 cm·a-1，而2015年6—9月黄河流域平均降水量较常年同期偏少24%，水储量变化总体趋势与降水在一定程度上线性相关.

由表4可以得出水储量变化滞后于降水的时间为2～3个月，原因为降水量经过一定时间的下渗等水文过程后转化为水储量从而被GRACE重力卫星探测到，也包括了观测月份之前的降雨.黄河流域上游地区水储量与降水的变化趋势基本一致，滞后2个月的EWH与降水相关性比中下游地区更强(r=0.31，p<0.01)，这主要是因为上游青藏高原、内蒙古高原水储量受自然因素影响较大，人为因素影响小；中游地区水储量与降水的滞后相关系数较低(r=0.22，p<0.01)，原因为中游黄土高原生态环境脆弱，水储量的影响因素较为复杂；而下游地区降水较为充沛，年际变化较大，而水储量与降水基本不相关(r=0.08，p>0.1)，下游华北平原人口稠密，人类生活、工业用水量较大，且由《黄河水资源公报》可知部分地区由于长期过量开采地下水，黄河流域已形成多个浅层地下水降落漏斗，导致降水量对于下游水储量的影响不占据主导因素.

4.1.2 蒸散发、土壤温度对EWH的影响

由图9a可以看出，黄河流域蒸散发量与土壤温度在2002—2020年间均呈现轻微上升趋势，而黄河流域年水储量呈明显下降趋势，其主要原因为土壤温度增高直接导致水分蒸散发的增多，而过高的蒸散发导致流域内水储量减少.流域蒸散发与土壤温度呈明显的季节性趋势，年内最大值出现在7—8月，此时的蒸散发与9—10月的水储量相关性较强(r=-0.31，p<0.05)，此时土壤温度与9—10月水储量相关性也最为显著(r=-0.4，p<0.05)，由此可见在夏季蒸散发与土壤温度均达到年内峰值，导致部分水储量通过水循环回到大气之中，而此水文过程大致需要2个月的时间.

由表4 还可知，对于黄河流域2002—2020年蒸散发、土壤温度时间序列与滞后2～3个月的水储量时间序列之间相关性最强，且蒸散发、土壤温度对于上游地区的水储量相关性影响较大，对中下游及整个黄河流域影响较小，这也和降水与水储量的相关性较为相似，而对于黄河流域整体滞后相关系数为正的原因为其相关性均不显著，且水储量受多种因素影响.GLDAS水文模型未能够充分考虑人类活动对蒸散发过程的影响，且由于其缺乏地下水模块而未能考虑地下水等因素对流域蒸散发的影响作用，而GRACE重力卫星则能够充分探测到流域内地下水和冰川等所有形式水资源的变化作用.总体而言，蒸散发与土壤温度对于水储量的影响是小于降水的，这与张璐等(2020)的结果一致.

4.2 EWH时间序列小波分析

相对于傅里叶变换，小波变换(Grinsted et al.，2004)在时域、频域中都能表现出优良的特性，利用该方法可以很好地将时间序列的周期性变化展现出来.本文采用连续小波分析(continuous wavelet transform，CWT)对2002—2020年共225个月GRACE反演的等效水高与GLDAS、CPC水储量时间序列进行功率谱分析，对其周期性进行探测，图10为连续小波分析的功率谱.从图10可以看出，基于GRACE、GLDAS与CPC数据解算的水储量都表现出了一定的周期变化特征，具体表现为均具有明显的周年周期信号，CPC水文模型计算的水储量周年信号最为明显，而2014—2017年水储量呈剧烈下降趋势，降水偏少，导致此期间GRACE与GLDAS计算的水储量周年信号不明显.

图10 GRACE、GLDAS及CPC计算的等效水高的小波分析Fig.10 The continuous wavelets transform of EWH by GRACE, GLDAS and CPC

图11 GRACE分别与GLDAS、CPC的交叉小波分析与相干小波谱分析Fig.11 The cross wavelets transform and wavelet coherence of EWH by GRACE with GLDAS and CPC

图12 GRACE与降水、蒸散发以及土壤温度的交叉小波分析Fig.12 The cross wavelets transform of GRACE with precipitation, evapotranspiration and soil temperature

为研究GRACE反演的等效水高与GLDAS、CPC水文模型得到的水储量之间的相关性和共振周期，分别对其时间序列进行了交叉小波(Cross Wavelet Transform，XWT)和小波相干谱分析(Wavelet Coherence，WTC)，结果如图11所示，图中的箭头方向表示二者相位的相关性，向右表示同相位，向左表示反相位，向下表示相位超前90°变化，向上表示相位超前270°或者延后90°变化(郭金运等，2015).交叉小波谱的大能量区基本都出现在整个时间序列的周年位置上(见图11a、b)，且相比于GRACE与GLDAS水储量之间共振周期，GRACE与CPC反演的水储量之间周年共振周期更为突出，说明基于GRACE反演的水储量与CPC水文模型结果在周年周期上相关性程度较高；由图11c、d相干小波谱分析可以看出，大部分的高值能量区都在影响锥线内，说明GRACE反演的等效水高与GLDAS、CPC水文模型得到的水储量较为一致，具有很强的相关性，且图中箭头大部分向右，说明两种数据计算的等效水高具有大致相同的相位.

对GRACE反演的黄河流域水储量分别与降水、蒸散量以及土壤温度进行交叉小波分析(图12)，以进一步分析其相关性.由图12交叉小波功率谱可以看出，GRACE反演的水储量与降水、蒸散量以及土壤温度之间的周年周期最为突出；在小于1周年的周期中，GRACE与降水、蒸散量之间会间断地出现一些高值能量带，例如降水、蒸散发在半周年的周期位置上高能量区出现在2012—2014年，说明在半周年周期位置上GRACE与二者也具有一定的相关性，但不如周年周期明显.周年周期的箭头均朝上，表明GRACE 反演的水储量相较于降水、蒸散量以及土壤温度变化滞后大致3个月，此结果与表3的结果相吻合.

5 结论

本文基于多层感知机重建了GRACE与GRACE-FO之间缺失的等效水高，研究黄河流域在2002—2020年水储量变化情况，并分析了降水、蒸散发、土壤温度与水储量的相关性，通过滑动平均方法与小波分析，讨论了黄河流域上中下游等效水高的时变规律.分析结果表明：

(1)基于多层感知机对GRACE与GRACE-FO之间缺失等效水高的重建有一定的可行性，MLP神经网络通过训练相关的输入参数后，可重建出精度较高的缺失等效水高，重建相关系数r均大于0.93(p<0.01).

(2)黄河流域水储量变化呈现出明显的季节性，水储量分别在秋季与春季达到最大值与最小值，整体呈现以-0.51±0.03 cm·a-1速率下降的趋势，2003—2004年水储量呈现明显的上升趋势后，在2004年春季达到最大值，此后直到2017年均大致呈现出不同程度的下降， 2017年后又呈现出上升趋势.黄河流域上游水储量以0.01±0.02 cm·a-1的速率大致持平，中游以-0.11±0.02 cm·a-1的速率轻微下降，上游与中游地区水储量与GLDAS水文模型相关系数r分别达到0.6与0.38(p<0.01)，而下游地区以-0.55±0.02 cm·a-1的速率显著下降.

(3)流域水储量变化受降水、蒸散发、温度及人类活动等因素的共同影响，GRACE反演黄河流域水储量变化相对于降水、蒸散发及土壤温度滞后时间达2～3个月，降水与水储量变化呈现出一致性，而水储量变化与蒸散发、土壤温度呈负相关，且降水对于水储量的影响大于蒸散发和土壤温度.上游与中游水储量受降水、蒸散发及土壤温度影响较大，而下游地区水储量受气象因素影响小，受人为因素影响较大.

(4)通过小波分析，验证了GRACE与GLDAS及CPC得到的陆地水储量具有很强的相关性，且均具有明显的周年共振周期；GRACE反演结果与降水、蒸散量以及土壤温度的周年共振周期同样明显.

致谢感谢CSR、JPL和GFZ提供的GRACE 卫星数据，GSFC提供的GLDAS水文数据，NOAA提供的CPC水文数据.感谢国家青藏高原科学数据中心(http:∥data.tpdc.ac.cn)提供中国区域基于降水重构陆地水储量变化数据.感谢审稿专家对本文提出的宝贵修改意见.