基于波数域梯度场分解的多尺度波形反演方法

李振春， 王自颖*， 黄建平， 崔超

1 中国石油大学(华东)地球科学与技术学院， 青岛 266580 2 海洋国家实验室海洋矿产资源评价与探测技术功能实验室， 青岛 266071

0 引言

在地震勘探领域，建立一个高精度的速度模型对地震成像和储层描述至关重要.全波形反演(Full Waveform Inversion, FWI)通过匹配观测数据与模拟数据中的所有波形信息建立目标泛函，利用局部优化算法，沿梯度方向不断更新得到精度更高的速度模型(Virieux and Operto, 2009).FWI的梯度是由正传的模拟波场与反传的残差波场做零延迟互相关计算得到的(Tarantola, 1984).反演过程中匹配的不仅仅是地震波场的走时信息，还有振幅及波形等动力学信息，因此FWI能够恢复地下模型中的细节构造.为了满足高精度地震勘探与开发的需求，建立更准确的速度模型，全波形反演近年来受到广泛关注.FWI面临的海量计算、“周波跳跃”、多参数反演等问题是一直以来的研究热点(李振春等，2020；邹鹏和程玖兵，2020；胡勇等，2021；潘冬雪等，2021；Wu et al.，2014；Chi et al.，2014; Kazei and Alkhalifah，2019; Wang et al.，2019；Yang et al.，2020；Yong et al.，2018，2019).

Wu和Toksöz(1987)首次讨论了反演中波数的分布，Mora(1989)指出全波形反演同时进行层析模式和偏移模式的更新.层析模式更新速度模型中的低波数成分，反演得到平滑的背景速度场.偏移模式则更新高波数分量，即更新含层界面信息的速度扰动，添加速度模型中的细节信息.对于反射地震数据，层析成分更新远比偏移成分弱，梯度场以高波数信息为主.在初始模型较差、缺少低频信息和大偏移距数据缺失时，反演结果易陷入局部极值，从而影响最终反演结果的精度(Yao et al.，2018，2020).

Liu等(2011)提出按照波场传播方向将地震波场分离为上行波场与下行波场，构造新的互相关逆时偏移成像条件，达到消除偏移结果中低频噪声的目的.Fei等(2015)发展了更为高效的波场分离算法，用于逆时偏移成像，该方法无需存储所有时刻的波场，节省了计算所需内存.Tang等(2013) 将这一成像条件应用到全波形反演中，将分离后的波场两两组合进行互相关，得到层析模式与偏移模式两种梯度，在反演前期提高长波长更新的权重，有效地提高了反演精度.Wang等(2016)发展了长波长成分与短波长成分交替更新的反演策略，也可以在一定程度上缓解低频缺失带来的局部极值问题.Chi等(2017)提出一种高效的梯度分解方法，利用反射系数引导波形反演，有效改善了深部构造的反演结果.除了根据上、下行波场分离进行梯度分解之外，Alkhalifah(2014)提出利用散射角滤波将波形反演梯度中的两成分分离.散射角滤波器的关键是计算震源波场与残差波场之间的角度，低波数成分由散射角接近180°的震源波场和残差波场构成.Yao等(2018)在平面波域实现了散射角滤波，解决了散射角滤波器基于速度各向同性的局限.然而这两种方法所需的内存和计算量较大，Yao等(2019)提出将梯度场变换到波数域加以低通滤波，利用非平稳平滑提取其中的层析成分，有效减小了计算量.还有学者提出反射波波形反演(Xu et al., 2012; Chi et al.，2015; Yao and Wu, 2017；Li and Alkhalifah，2020)，将常规波形反演的梯度分为背景模型和扰动模型的梯度两部分.与波场分离和角度滤波的方法不同的是，该方法通过引入Born正演，基于波动方程的线性化近似，将震源正传及残差反传得到的波场分别分解为背景波场与散射波场.然后对四个波场进行两两互相关，构造两部分梯度.

基于波形反演梯度分解的思想，本文将波形反演分为层析与偏移两种模式.在反演初期采用层析模式，发展了一种基于波数域梯度场分解的多尺度波形反演方法.利用Hilbert变换隐式分离上、下行波，计算层析模式梯度场，并在波数域进行低通阈值控制.该方法能够有效地更新速度模型中长波长成分，同时压制层析模式梯度场中剩余的偏移成分噪声.利用简单模型和Marmousi模型的测试结果表明，本文所提出的方法可以有效更新速度模型中的低波数成分，为常规全波形反演提供良好的初始模型，取得了较好的反演结果.

1 基本原理

1.1 时间域全波形反演理论

在时间域，二维各向同性常密度声波方程可以表示为：

+δ(x-xs)S(t)，(1)

式中，v(x)是速度，u(x,t,xs)是正演模拟在t时刻于空间位置x处的波场，xs为震源的空间位置，S(t)是震源时间函数.

全波形反演是一个非线性的最优化问题，通常将目标函数定义为观测数据与数值模拟数据之间残差的L2范数：

(2)

式中，E(m)为全波形反演的目标函数，u(xr,t;xs)表示通过正演模拟得到的地震记录，uobs(xr,t;xs)表示为观测地震记录，xs和xr为炮点与检波点的位置，tmax表示地震记录的时间长度.采用梯度类的局部优化算法，通过迭代的方法在初始速度模型v0附近寻找目标函数的极值.基于伴随状态法(Plessix, 2006; Fichtner and Trampert, 2011)，目标函数对速度的梯度通过计算正传震源波场与反传残差波场的零延迟互相关得到：

(3)

式中，GFWI表示全波形反演的梯度，t为时间，v(x)表示速度模型参数.ures(x,t;xs)为残差反传波场，即采用观测记录与模拟记录之差为伴随源：

Sadj(xr,t;xs)=u(xr,t;xs)-uobs(xr,t;xs)，(4)

计算伴随波场的波动方程可表示为：

+Sadj(xr,t;xs)，(5)

本文全波形反演采用的局部最优化方法为共轭梯度法，反演迭代的更新方向dk由本次迭代的梯度GFWI,k与上一次迭代的更新方向dk-1线性组合，表达式为：

dk=-GFWI,k+βkdk-1，k≥1，(6)

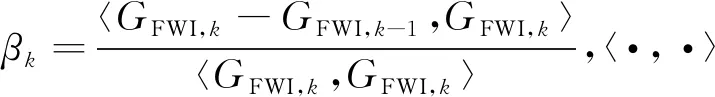
基于共轭梯度法计算得到的下降方向dk，模型迭代更新公式表示为：

vk+1=vk+akdk，(7)

式中，vk表示在第k次迭代时的速度模型，ak为步长，通过线搜索的方式获得(Pica et al., 1990).

1.2 全波形反演梯度分解方法

Mora(1989)提出“全波形反演=偏移+层析”，即全波形反演具备两种功能：一是偏移，更新层界面信息；二是层析，更新背景速度.因此，全波形反演的梯度可分解为两部分，表达式为：

GFWI=Gb+Gp，(8)

式中，Gb为背景速度更新量，主要为长波长成分，Gp为层界面信息更新量，主要为短波长成分.当地震数据以反射波为主时，全波形反演梯度由层界面信息更新量为主导，背景速度更新量相对较小而被压制，若初始模型与真实模型相差较远，则会导致反演陷入局部极值，无法重构高精度速度模型.

为了缓解这一问题，可以将全波形反演的梯度中层析成分与偏移成分分离，在反演过程中提高层析成分在梯度中的比重，使反演中的速度更新以长波长的背景速度更新为主.传统的全波形反演梯度为正传震源波场与反传伴随波场的互相关.本文根据地震波传播方向将波场分解为上行波场与下行波场，梯度中的偏移成分由空间上传播方向相反的震源波场与伴随波场进行互相关得到：

(9)

式中，S和R分别表示正传和反传波场，角标u和d分别代表波场的传播方向为上行和下行.梯度中的层析成分由空间上传播方向相同的震源波场与伴随波场进行互相关得到：

(10)

本文基于Hilbert变换进行隐式的波场分离(Chi et al., 2017)，梯度可表示为：

(11)

式中，Hz表示沿深度z方向的Hilbert变换.令λ=1，该式为层析梯度；令λ=-1，该式为偏移梯度.该隐式波场分离方法只在空间域进行一维Fourier变换，与频率-波数域波场分离方法相比，不需要存储所有时刻的波场，大大节省了波场分离带来的内存和计算负担.在反演的初期，我们以长波长成分的更新为主，用于构建良好的背景速度模型，因此在迭代过程中采用层析梯度，表示为：

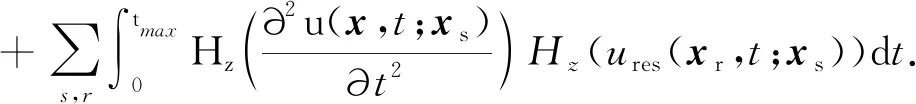
(12)

1.3 基于波数域梯度场分解的多尺度波形反演方法

根据上下行波场进行梯度场分解的方法存在偏移成分泄露问题，导致在高陡断层附近存在高波数假象.一种方法就是在波数域控制梯度更新的长波长成分(Yao et al., 2018)，本文设计了多尺度的二维波数域低通滤波器，以压制梯度分解后在层析梯度中残余的高波数成分.该二维波数域低通滤波器表示为：

(13)

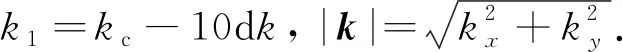
通过在分解的层析梯度之上加以波数域的滤波并控制截断波数，我们可以得到不同尺度的低波数梯度更新量，从而实现多尺度反演，为全波形反演建立良好的初始模型.由于该滤波器在每次迭代中应用一次，所增加的计算量相比于波场模拟和梯度分解是可以忽略的.

本方法的反演流程如图1所示：(1)由地震波场正演模拟得到合成地震记录，与观测记录作差得到残差波场；(2)将检波点的残差反传得到残差波场；(3)对波场沿深度方向作Hilbert变换，互相关得到波形反演的层析梯度；(4)应用波数域滤波器，压制残余的高波数偏移成分；(5)迭代结束，更新速度模型；(6)经过多个反演阶段多个尺度的波数域滤波，输出速度模型，再采用常规波形反演获取高分辨率速度模型，得到最终结果.

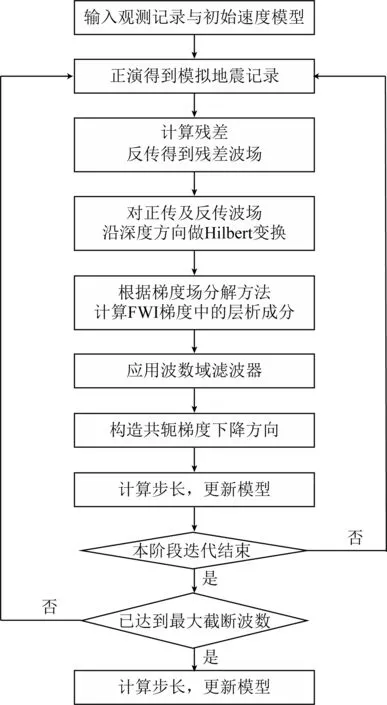
图1 基于波数域梯度分解的多尺度波形反演流程Fig.1 Work flow of multi-scale full waveform inversion based on gradient decomposition in wavenumber domain (WGDFWI)

2 模型试算

根据以上提出的基于梯度分解的多尺度波形反演方法，本文首先利用双层简单模型，采用单震源、单接收点的观测系统，测试梯度分解的正确性和有效性.然后将该方法应用到Marmousi模型，采用多尺度反演策略，测试该方法对复杂模型的反演效果，并与常规波形反演结果进行对比，验证了本文所提出反演方法的有效性.

2.1 全波形反演敏感核函数测试

首先采用双层简单模型测试全波形反演的敏感核函数.真实模型纵横大小为5 km×5 km，网格间距为10 m.图2a中黑色实线为层界面所在位置.真实模型第一层速度值为2.0 km·s-1，第二层速度值为3.0 km·s-1.采用的初始模型具有与真实模型相同的构造，第一层速度值为2.0 km·s-1，第二层的速度值为2.95 km·s-1.

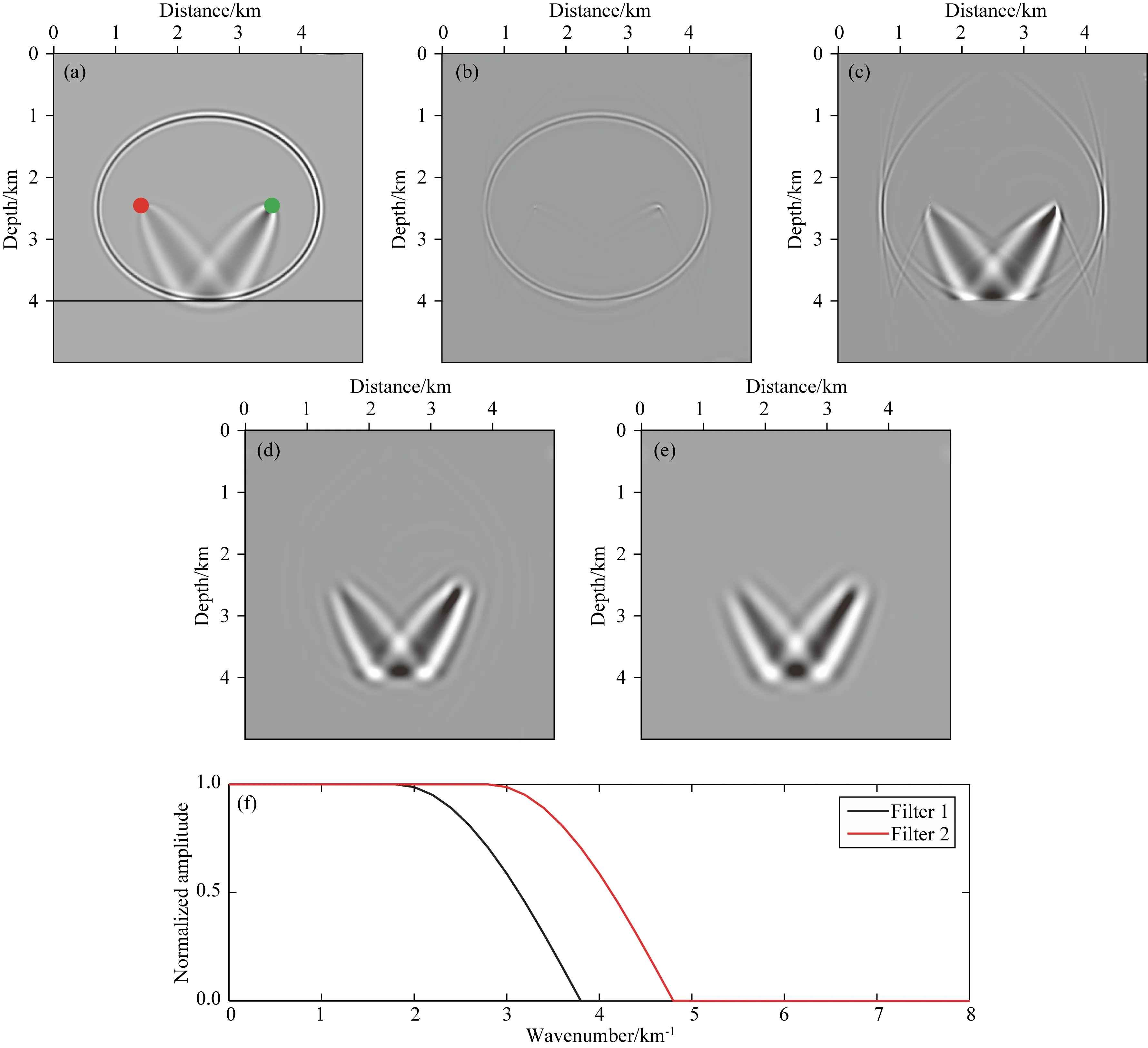
图2 全波形反演敏感核函数(a) 常规全波形反演敏感核函数； (b) 梯度分解得到的偏移成分； (c) 梯度分解得到的层析成分； (d) 将图(c)进行波数域滤波，使用图(f)中所示波数域滤波器2(红)； (e) 将图(c)进行波数域滤波，使用图(f)中所示波数域滤波器1(黑)； (f) 波数域滤波器.Fig.2 FWI sensitivity kernel(a) The sensitivity kernel of conventional FWI; (b) Migration component after decomposition; (c) Tomographic component after decomposition; (d) Wavenumber domain filtered tomographic component, using the filter 2 in fig.(f); (e) Wavenumber domain filtered tomographic component, using the filter 1 in fig.(f); (f) Wavenumber domain filter.

采用主频为10 Hz的雷克子波.震源所在深度为2500 m，横向位置为1500 m.接收点所在深度为2500 m，横向位置为3500 m.震源和检波点位置如图2a红色圆点与绿色圆点所标示.计算常规全波形反演梯度，得到的波形反演敏感核函数(图2a).椭圆形偏移圈为波形反演提供层界面信息更新量，“兔耳朵”形状的层析成分能够在迭代中提供低波数背景模型的更新量.

采用以上提出的隐式波场分离方法，我们根据波场的传播方向，将波形反演的梯度分解为两部分.基于公式(11)，令λ=-1，可以提取出其中的偏移成分.如图2b所示，敏感核函数中只含有椭圆形的偏移圈.令λ=1，可以提取出其中的层析成分.如图2c所示，敏感核函数中偏移圈被压制，层析成分的振幅被大大提升，可以有效增强长波长成分更新.

从图2c可以看出，在敏感核函数两侧仍有未被完全压制的高波数成分.这表明梯度分解之后的层析成分中存在偏移成分泄露的现象，表现为大倾角的反射轴.由于波场只按照垂直传播方向分离，而对于倾角较大的反射面，虽然其正传与反传波场的传播方向在水平方向上方向相反，但其在垂直方向上同向，因此在提取的层析成分中形成高波数假象.本文应用波数域低通滤波器优化层析成分梯度，有效地压制了剩余的偏移成分，缓解了偏移成分泄露问题，如图2d、e所示.另外，通过在波数域控制低通滤波的截断波数(图2f)，可以得到含有不同波数成分的层析梯度，这一优化的层析成分梯度能够为波形反演提供更有效且较为稳定的背景模型更新.

2.2 Marmousi模型测试

本文以Marmousi模型为例进行试算，以验证本文方法的有效性和稳定性.真实模型纵横大小为9204 m×2760 m，网格数目为767×230，网格间距为12 m，在真实速度模型上采用10 Hz雷克子波作为震源子波进行正演模拟，时间采样间隔0.001 s，检波器记录总时间长度为4 s，得到观测数据.总炮数为153炮，炮间距60 m.采用全接收的观测系统，检波器间隔为12 m，深度为12 m(图3a).将真实模型进行平滑，作为反演的初始模型(图3b).该初始模型与真实模型相差较大，直接进行常规全波形反演，会导致反演过程中观测数据和模拟数据的波形不匹配的问题.“周波跳跃”使反演迅速落入局部极值，难以得到与真实模型接近的反演结果.由图4可以看出，速度模型浅部高陡断层附近存在高速异常的假象，深部背斜构造也未得到良好恢复.

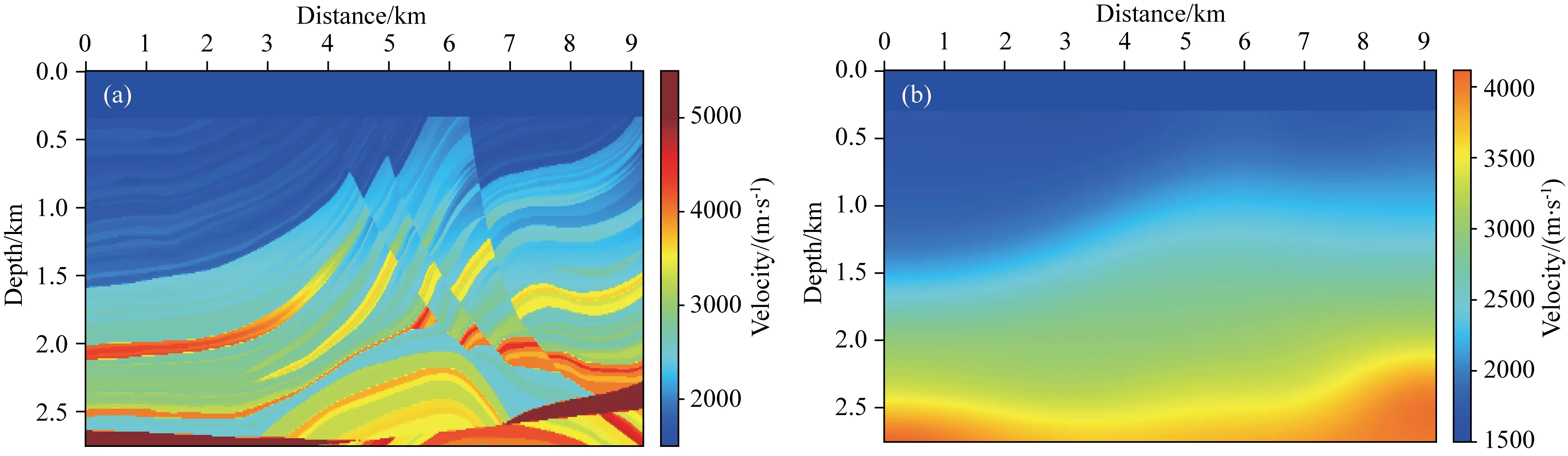
图3 Marmousi速度模型(a) 真实速度模型； (b) 初始速度模型.Fig.3 Marmousi velocity model(a) True velocity model; (b) Initial velocity model.

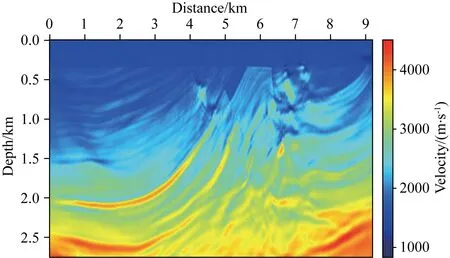
图4 常规全波形反演结果Fig.4 Conventional FWI result

将本文提出的方法应用于该复杂模型，可为常规波形反演建立良好的初始模型.为了提高反演的稳定性，采用四个截断波数不同的二维波数域滤波器(图5)，将该滤波器应用于每次迭代计算得到的梯度，以缓解梯度分解后的层析成分中偏移泄露的问题.四个阶段的多尺度反演过程中，每个阶段迭代30次，各反演阶段的结果如图6所示.在反演前期，恢复了大尺度的速度模型信息，反演结果平滑且没有高波数假象.随着截断波数的增大，逐渐恢复出更多较为细节的速度模型构造信息.

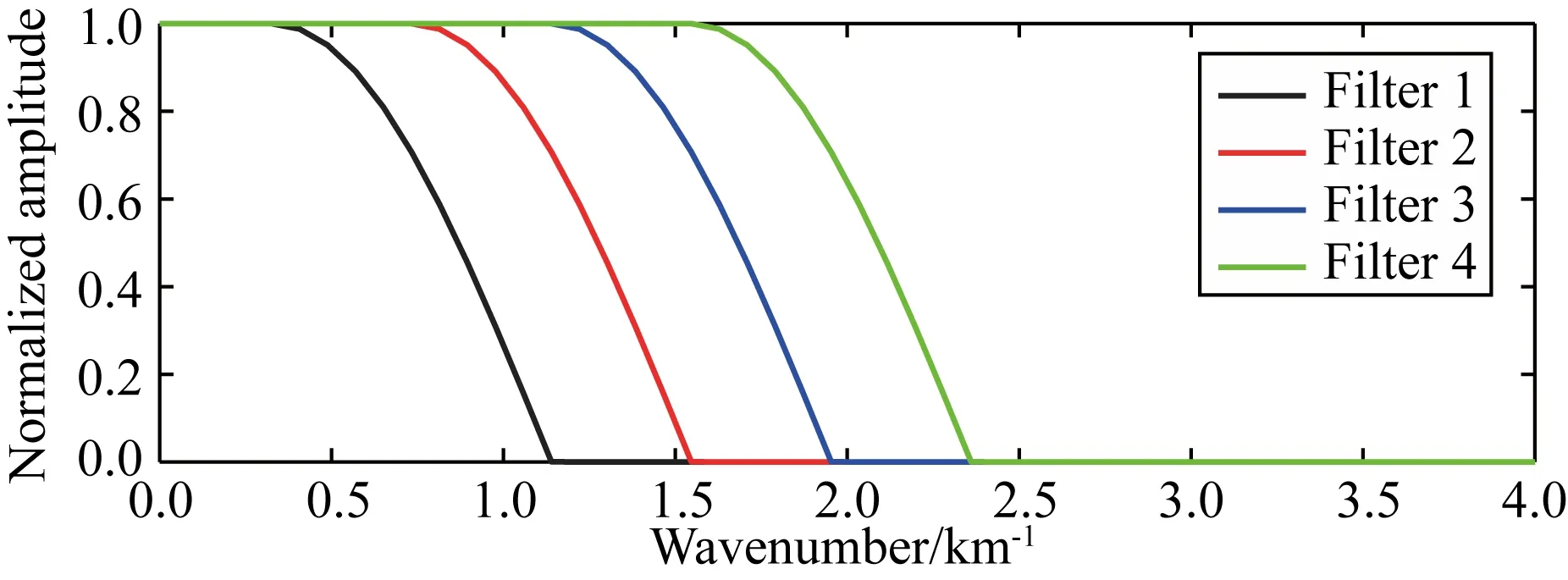
图5 四个反演阶段的波数域低通滤波器Fig.5 Wavenumber domain filters in the four scale inversion stages

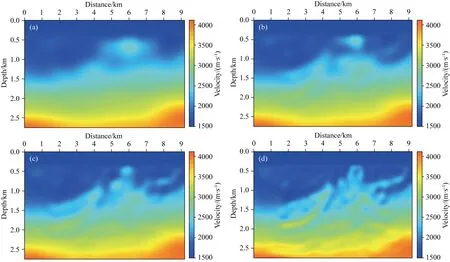
图6 基于多尺度波数域梯度分解方法的波形反演结果(a) 采用最小截断波数的滤波器1得到的反演结果； (b) 提高截断波数，采用滤波器2得到的反演结果；(c) 采用滤波器3得到的反演结果； (d) 在最后一个反演阶段，采用滤波器4得到的反演结果.Fig.6 Inversion results of multi-scale FWI based on gradient decomposition in wavenumber domain(a) Inversion result using filter 1; (b) Inversion result after increasing cut-off wavenumber using filter 2; (c) Inversion result using filter 3; (d) Inversion result using filter 4.

将反演结果(图6d)作为初始模型，进行常规波形反演，得到高分辨率的最终波形反演结果.由图7可以看出，本文方法可以给出相对准确的反演结果.相比于常规全波形反演，本文方法高精度地重构了浅层的断层构造，同时也恢复出深层背斜构造的基本形态.

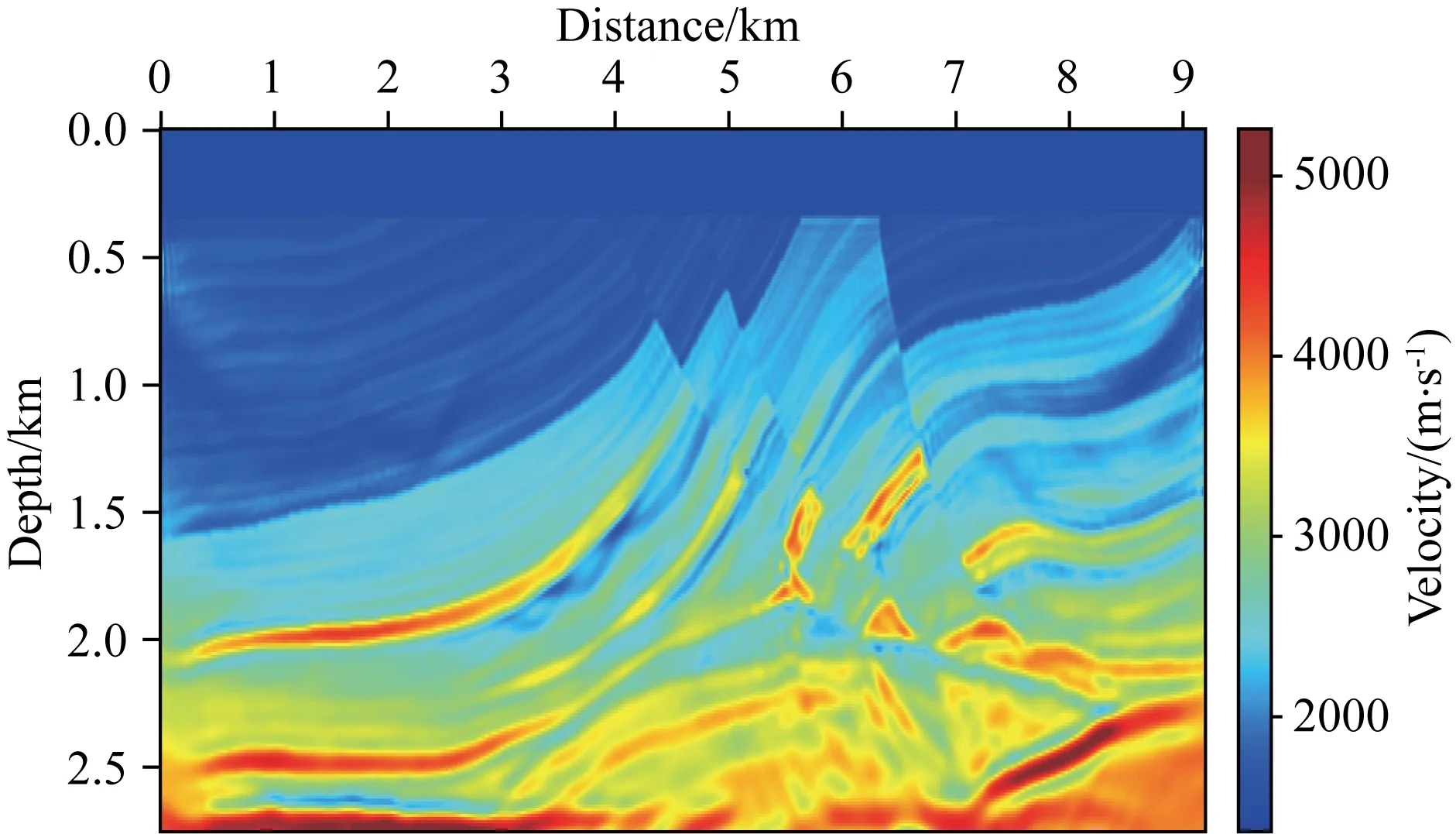
图7 最终波形反演结果Fig.7 Final inversion result

分别在三个位置抽取速度模型的纵向曲线，单道对比结果如图8所示.速度模型抽取单道的横向位置分别为2640 m，4320 m，6000 m.对比真实速度、初始速度与反演结果的单道曲线，可以看出基于梯度分解的多尺度波形反演结果与真实模型更为接近.本文方法相较于常规波形反演，对于浅-中层的反演结果基本准确，且没有高速异常假象，在深层的反演效果也有明显提升.

图8 速度模型抽取单道对比(a) 2640 m处速度曲线； (b) 4320 m处速度曲线； (c) 6000 m处速度曲线.Fig.8 Comparison of velocity traces(a) Distance=2640 m; (b) Distance=4320 m; (c) Distance=6000 m.

为了证明本文方法策略的有效性，分别进行仅采用梯度分解的波形反演方法(GDFWI)和仅应用多尺度波数域滤波器的波形反演方法(WFFWI)的两组反演测试，反演结果分别如图9、图10所示.图9a中模型的低波数成分得到了一定的更新，最终反演精度相较于常规波形反演也有所改善.然而偏移泄露问题使构建的背景速度模型中存在大倾角的高波数异常，导致最终反演结果(图9b)在浅层存在少量高波数噪声，中深层构造也与真实模型仍有较大差异.若仅将多尺度波数域滤波应用于常规波形反演的梯度，且采用相同的波数域滤波器和反演流程，反演结果如图10所示.反演效果略优于常规全波形反演，但速度结构信息也无法得到准确恢复，部分高速异常假象依然存在.

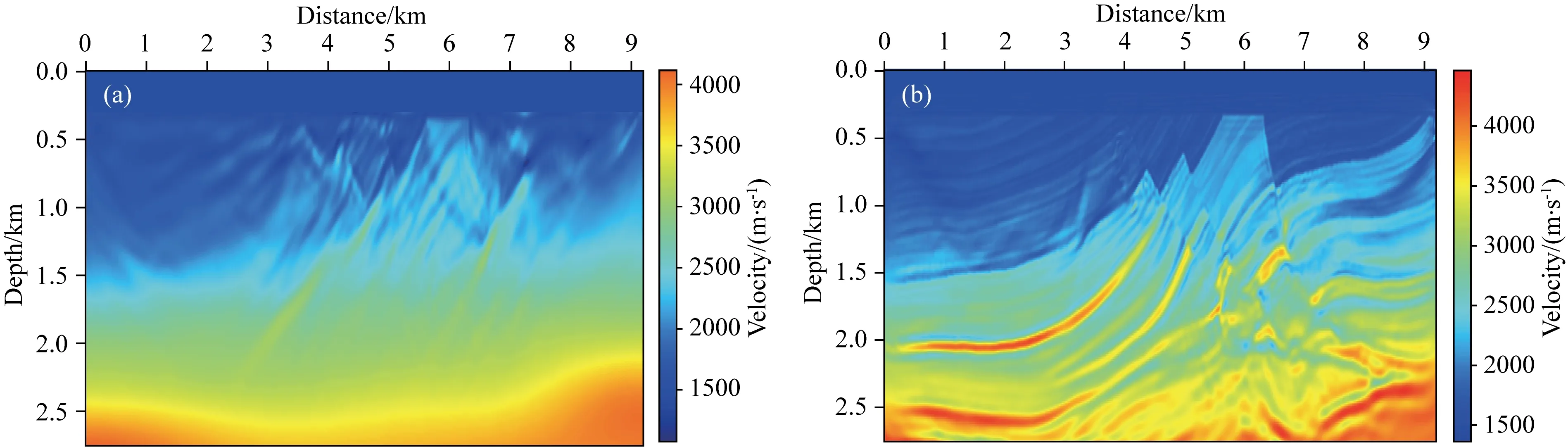
图9 梯度分解的波形反演(GDFWI)结果(a) 仅采用梯度分解的波形反演结果； (b) 以图(a)为初始模型进行常规波形反演的最终结果.Fig.9 Gradient-decomposition full waveform inversion result(a) Inversion result only based on gradient decomposition; (b) Waveform inversion results using fig.(a) as initial model.

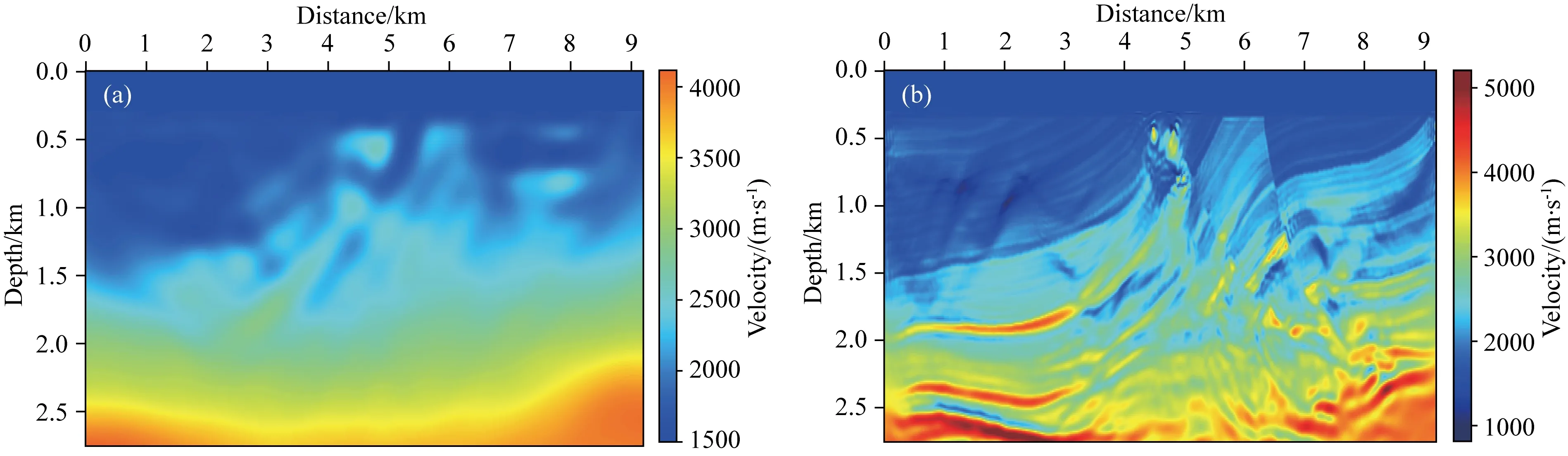
图10 多尺度波数域滤波波形反演(WFFWI)结果(a) 仅应用波数域滤波器进行多尺度波形反演结果； (b)以图(a)为初始模型进行常规波形反演的最终结果.Fig.10 Wavenumber-domain filtered full waveform inversion result(a) Waveform inversion result only based on wavenumber-domain filter; (b) Waveform inversion results using fig.(a) as initial model.

图11给出了反演的归一化目标泛函收敛曲线.反演前期利用三种方法(WGDFWI, GDFWI, WFFWI)恢复低波数信息的反演收敛曲线如图11a所示.以该三种方法建立的背景速度模型作为初始模型进行常规波形反演的目标泛函收敛曲线如图11b所示.与常规波形反演的收敛曲线对比，可以看出本文方法的目标泛函收敛至更小的数值.综上，基于波数域梯度分解的多尺度波形反演方法能够更为稳定有效地更新背景速度模型，以此作为常规波形反演的初始模型能够获得更高精度的反演结果.

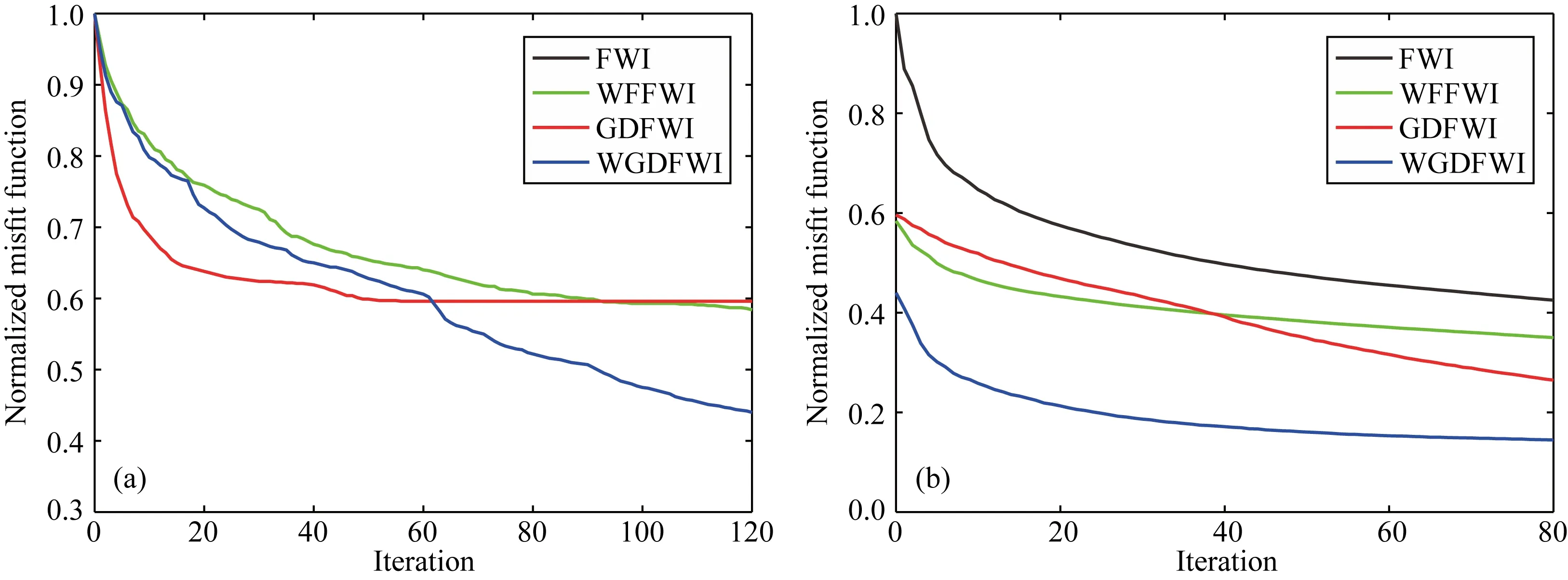
图11 归一化目标泛函收敛曲线(a) WFFWI、GDFWI、WGDFWI三种波形反演方法构建背景速度模型的目标泛函收敛曲线； (b) 将初始速度模型和三种波形反演方法构建的背景速度模型作为输入速度模型进行常规波形反演的目标泛函收敛曲线.Fig.11 Normalized misfit function convergence curves(a) Misfit convergence curves at the early stage using WFFWI, GDFWI, WGDFWI to reconstruct background velocity model；(b) The later stage using conventional FWI.

2.3 有限偏移距反射波波形反演模型测试

在实际情况中，地震数据往往采用移动接收方式，偏移距较小，观测数据以反射波为主.因此，本节利用有限偏移距的反射波数据对本文方法进行测试，以验证本文方法在限制偏移距情况下的有效性.

采用的真实模型(图12a)纵横大小为9204 m×2760 m，网格数目为767×230，网格间距为12 m.采用12 Hz雷克子波作为震源子波进行正演模拟得到观测记录，时间采样间隔0.001 s，检波器记录总时间长度为3 s.总炮数为127炮，炮间距72 m.采用两边接收的移动观测系统，检波器间隔为12 m，深度为12 m，最大偏移距为2400 m，仅保留炮记录中的反射波作为观测数据.反演的初始模型如图12b所示.

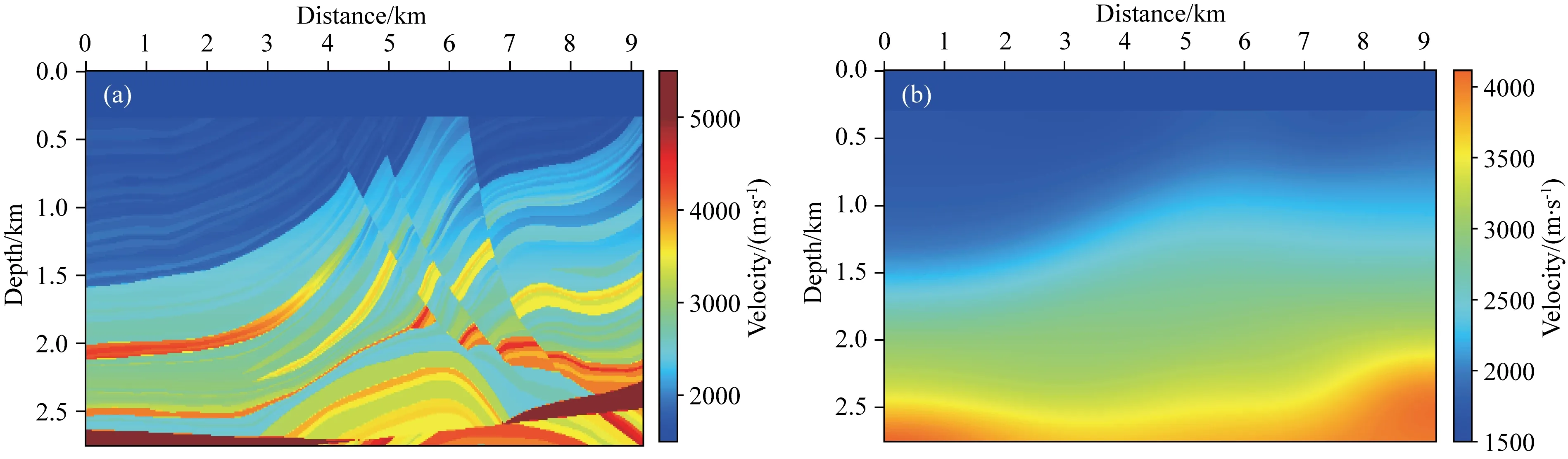
图12 Marmousi速度模型(a) 真实速度模型； (b) 初始速度模型.Fig.12 Marmousi velocity model(a) True velocity model; (b) Initial velocity model.

图13为观测数据的偏移距有限时，本文方法在反演前期构建的背景速度模型.反演过程中采用的二维波数域滤波器和反演流程与2.2小节保持一致.图14为本文方法与常规波形反演的最终结果.图15为反演结果抽取1500 m、6000 m、7500 m位置处纵向速度曲线对比.常规波形反演能够基本恢复浅层的基础构造，但存在一些高波数噪声；对于中-深层构造，常规波形反演以偏移成分更新为主，对含有低波数成分的层内速度信息未能实现精确反演，导致最终结果不准确.本文方法在反演前期强调了低波数的层析成分更新，有效避免反演陷入局部极值，实现了较高精度的速度建模.从抽取的速度曲线可以看出，本文方法最终反演结果更接近真实速度模型.

图13 多尺度波数域梯度分解的背景速度模型反演结果Fig.13 Inverted background velocity model of multi-scale FWI based on gradient decomposition in wavenumber domain

图14 多尺度波数域梯度分解的波形反演最终结果(a)与常规波形反演结果(b)Fig.14 Results of multi-scale FWI based on gradient decomposition in wavenumber domain (a) and conventional FWI (b)

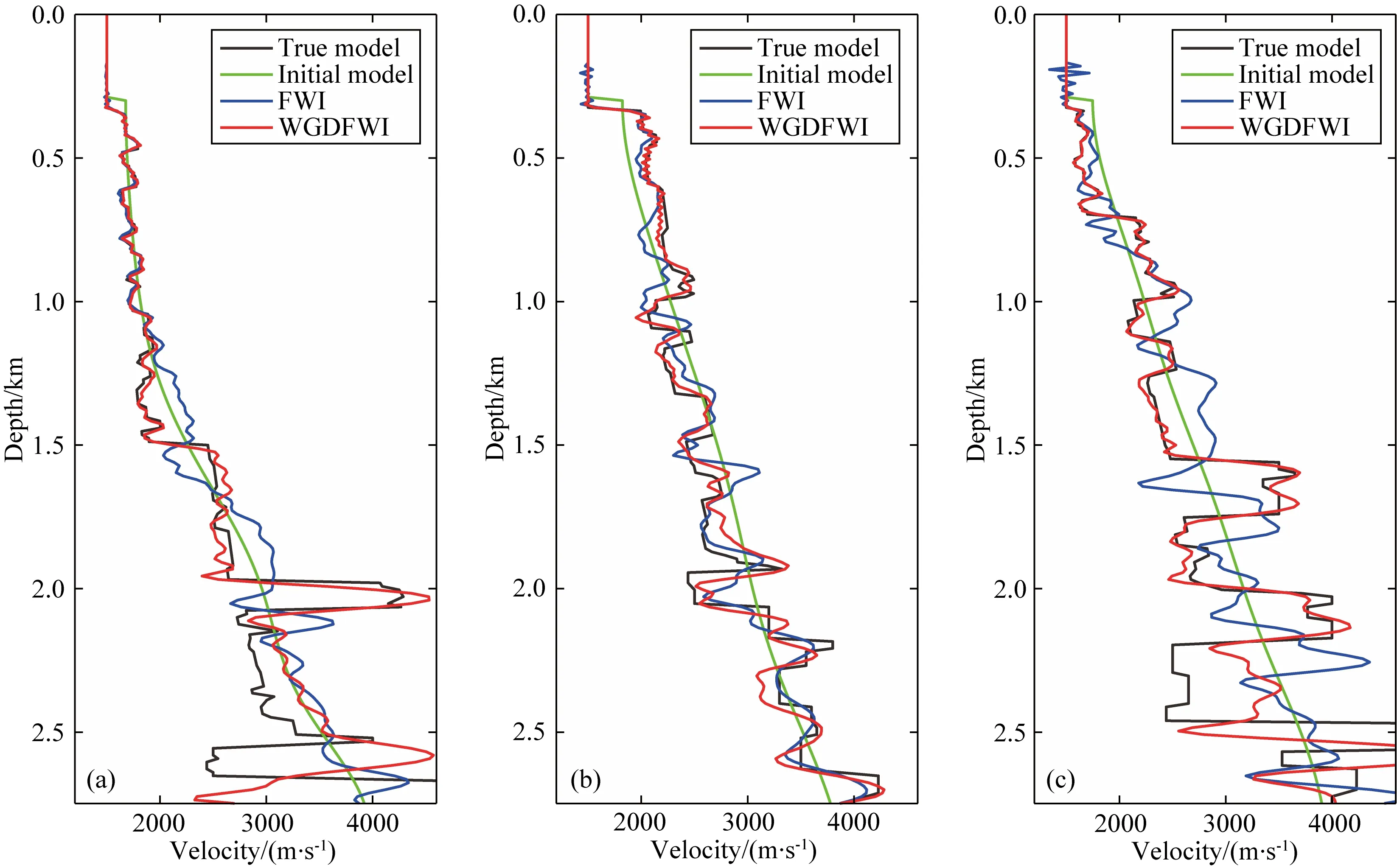
图15 速度模型抽取单道对比(a) 1500 m处速度曲线； (b) 6000 m处速度曲线； (c) 7500 m处速度曲线.Fig.15 Comparison of velocity traces(a) Distance=1500 m; (b) Distance=6000 m; (c) Distance=7500 m.

3 结论

本文对时间域全波形反演方法进行了研究，针对波形反演中低波数成分更新相对较弱，反演易陷入局部极值的问题，根据波场传播方向进行隐式波场分离，提取出梯度中的层析成分，先利用多尺度层析梯度反演构建低波数背景速度模型，然后以此为初始模型，采用常规的波形反演方法来获取高分辨率模型.从波形反演敏感核函数分析的结果可以看出，该梯度分解方法能够增强梯度中低波数成分的振幅，压制大部分的偏移成分，波数域滤波可以有效消除剩余的高波数假象，缓解偏移成分泄露的问题.利用复杂模型进行数值实验的结果表明，该方法能够稳定而有效地更新大尺度的背景速度模型信息，为常规全波形反演提供良好的初始模型，提高最终反演结果的精度.

致谢感谢中国石油大学(华东)地震波传播与成像(SWPI)课题组的支持与帮助，感谢审稿专家提出的修改意见.