基于ELMD-SVD和Prony的谐波间谐波检测方法

刘士绮，王雅静，梅宇，张祥珂，施瑶，窦震海

（山东理工大学电气与电子工程学院，山东 淄博 255049）

近年来，随着新能源领域的发展以及非线性负荷和电力电子设备的大量使用，导致了电力系统信号中主要由谐波和间谐波引起的波形失真。为了保证输配电网的电能质量，必须对电力信号的谐波进行有效的检测与分析[1]。目前，常用的谐波检测的方法主要有快速傅里叶变换（fast Fourier transform，FFT）[2]、小波变换[3]、Prony 算法[4]、希尔伯特-黄变换（Hilbert-Huang transform，HHT）[5]等。其中FFT具有频谱泄露、栅栏效应等问题，且不能处理非线性和非平稳信号。小波变换具有多分辨率特性，可分析非平稳、非线性信号，但是其结果不是实时频谱，不适合于直观分析，此外其分辨率取决于不同母小波的选择，且基函数的选择也尚无明确理论指导[6]。基于经验模态分解（empirical mode decomposition，EMD）的HHT方法可将原始信号分解成一系列固有模态函数（intrinsic mode functions，IMFs），然后用希尔伯特变换（Hilbert transform，HT）对其进行分析，但EMD存在过度分解、模态混叠和端点效应等问题[7]。

Prony方法具有频率分辨率高和计算简单的优点，但其对噪声非常敏感[4]，对待检测信号的信噪比要求较高，通常需结合降噪算法对信号进行预处理。

为解决噪声对Prony算法在谐波参数辨识时的影响，文献[8]提出先将信号进行EMD分解去掉噪声IMF分量，然后进行Prony分析的方法，但EMD存在虚假分量、模态混叠、端点效应等问题，去噪的同时也丢失了大量有效信息。文献[9]采用集成经验模态分解（ensemble empirical mode decomposition，EEMD）降噪方法，EEMD抑制了EMD存在的模态混叠效应，提高了去噪效果，但EEMD的白噪声辅助分析方法可能造成更多虚假IMF分量。局部均值分解（local mean decomposition，LMD）是一种新的时频分析方法，由Jonathan S Smith[10]于2005年提出，它可以将复杂的多分量信号自适应分解成一组由高频到低频排列的乘积函数，由于不需进行希尔伯特变换，从而有效地避免了EMD和EEMD的无法解释的负频率问题，且抑制端点效应和模态混叠能力均强于EMD[11]。文献[12]提出LMD与奇异值分解（singular value decomposition，SVD）结合的微震信号降噪方法，由于LMD规避了EMD的诸多缺陷，相比以上算法进一步提高了降噪效果，但仍无法完全消除模态混叠对降噪带来的负面影响。集成局部均值分解（ensemble local mean decomposition，ELMD）是基于LMD并结合EEMD的白噪声方法提出的一种改进算法[13]，该方法抑制了LMD的模态混叠效应同时不存在EEMD的虚假分量问题。

本文提出一种基于ELMD-SVD和Prony的谐波检测方法，先利用ELMD的高通和一系列带通滤波器的滤波器组结构对电力系统信号进行初步降噪，再用奇异值分解针对残留噪声进行二次降噪，最后对降噪后信号利用Prony提取信号参数。仿真结果表明，该方法能最大程度滤除噪声且保留信号原始特征，准确的辨识出谐波信号的幅值、频率和相位参数。

1 基本原理

1.1 Prony算法基本原理

1.2 ELMD基本原理

ELMD是在LMD基础上引入白噪声辅助分析的一种改进算法。LMD能够把多成分信号分解为一系列频率由高到低排列的乘积函数（product functions，PF）分量，每个PF分量应只包含一个频率成分，然而研究表明信号的间歇性会造成原始LMD的模态混叠问题，该问题导致LMD将信号分解为一些物理意义不明确的PF成分，即一个PF分量可能包含不同的时间尺度，使信号与噪声无法完全筛分，影响去噪效果。

为抑制LMD的模态混叠，ELMD将白噪声辅助分析方法引入到LMD中，在LMD方法自适应分解前对信号重复加入M次均值为零的高斯白噪声，白噪声均匀分布在各个频段上，可以引导信号自适应分布到合适的频段上，改善了极值点分布不均匀的缺陷，可有效抑制模态混叠。主要步骤如下：

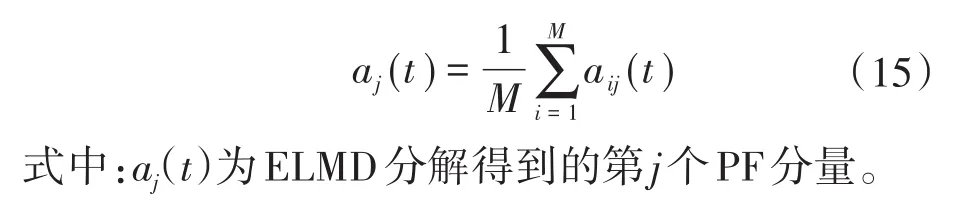
虽然ELMD有效抑制了LMD的模态混叠效应，但从EMD，LMD及其所有相关改进算法的本质来说，迭代算法上一层分解得到的结果会用到下一层的分解过程中，因此噪声在每层PF分量中都有混叠，只是程度不同。舍弃掉ELMD分解结果的高频部分，会造成部分低频有用信息随着高频PF分量被去除而丢失，而部分高频噪声又遗留在低频PF分量中。

要实现有效降噪需对ELMD分解结果进行筛选，分辨出噪声分量和有效分量。因此，引入K-L散度（Kullback-Leibler divergence）法确定噪声分量与有效分量分界点，将分界点之前的噪声分量剔除，对剩余分量予以保留，实现降噪的同时最大程度避免丢失信号有效信息。

1.3 K-L散度原理

ELMD将含噪信号分解为从高频到低频分布的一系列PF分量，因此引入信息论中K-L散度法区分噪声分量和有效分量。K-L散度被广泛用于度量两个分布之间的相似性[14]，算法如下：

基于这一理论，依次将各PF分量与原信号作为两个集合，采用K-L散度对各个PF分量与原信号的相似程度进行界定。与原信号相似性越高的PF分量K-L散度越小。根据K-L散度特点，针对电力系统信号，分量K-L散度越大说明其为噪声分量的可能性就越大。将各分量与原信号的K-L散度按照式（21）归一化至[0，1]区间。其中x为K-L散度值，xmax和xmin分别为K-L散度最大值和最小值，y为归一化值。归一化后设置阈值c，对高于阈值c的分量为噪声分量，低于阈值c的分量为有效分量。

ELMD借助白噪声在求平均时相互抵消的思想，将M次分解得到的PF分量的平均值作为最终的分解结果，可以排除白噪声分量得到真实分量，然而有限次的平均并不能使白噪声完全消除。目前常用的小波变换消噪法受基小波、阈值选择等问题的影响，消噪能力并不十分理想，因此使用奇异值分解方法进一步消除白噪声残留和模态混叠带来的工程噪声残留：

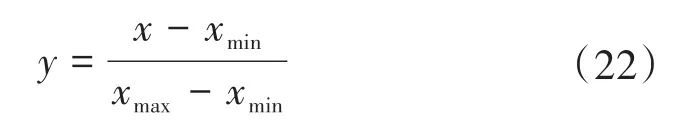
1.4 奇异值分解基本原理

根据奇异值分解理论和Frobeious范数意义下矩阵最佳逼近定理得到：有用的信号主要由前r个较大的奇异值反映，噪声信号由后面较小的奇异值反映，保留较大奇异值将余下奇异值置零，形成新的对角矩阵D带入式（24）进行逆变换获得降噪重构后的信号。因此，奇异值分解降噪的关键在于重构个数r的选择。

1.5 奇异值分解阶数确定

以原始信号主频个数的两倍作为奇异值有效秩阶次的方法对仿真信号取得了较好的效果[15]，而文中方法在SVD之前已经通过ELMD初步降噪，因此对实际工程中的复杂工况仍有良好的适应性。采用FFT提取信号主频个数，从而确定奇异值有效秩阶次。

2 ELMD-SVD-Prony算法

2.1 算法思路

虽然ELMD抑制了LMD的模态混叠效应，但对分解结果直接去除高频PF分量的做法仍可能造成部分有效信息丢失，因此本文采用ELMD分解得到PF分量，然后计算各PF的K-L散度，将含噪分量予以剔除，对剩余有效分量进行SVD二次降噪，最后结合Prony提取谐波参数。该算法可有效降噪同时不丢失信号有效信息，提升Prony检测精度。

2.2 联合处理过程

ELMD-SVD-Prony算法联合处理过程如下：

1）对含噪信号进行ELMD分解，得到L个PFi（t），i=1，2，…，L以及余项u（t）。

2）分别计算各PFi（t）分量与原始含噪信号的K-L散度并归一化，K-L散度方法区分度较高，本文针对电力系统信号进行大量实验后将阈值c设置为0.5。将高于阈值的n个PF中前n-1个予以剔除，第n个PF为分界分量，由于分界分量中会含有部分有效信息故予以保留。

3）对分界分量及剩余PF分量利用奇异值分解降噪，奇异值阶数根据信号主频个数确定。

4）将奇异值分解降噪后的各PF分量与余项u（t）累加重构得到最终降噪结果。

5）对联合降噪处理得到的信号进行Prony分析，获得谐波参数。

2.3 算法流程图

本文所提算法流程图如图1所示。

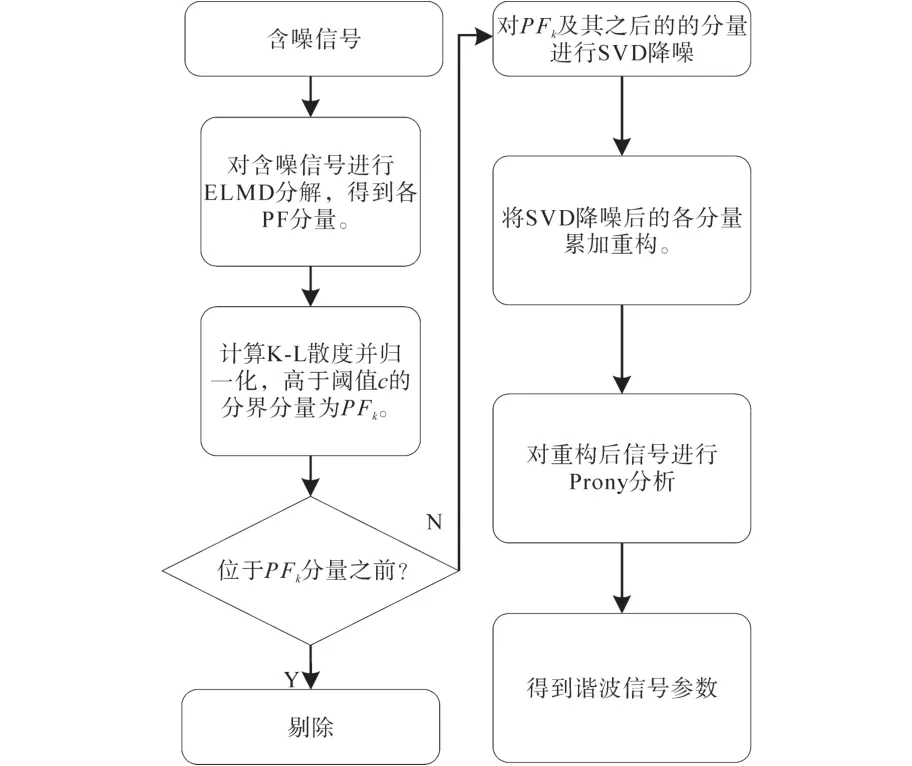
图1 算法流程图Fig.1 Algorithm flow chart

3 仿真分析

电力系统模拟信号如下：

仿真参数设置如下：采样频率10 kHz，采样点数3 000，采样时长0.3 s。将20 dB高斯白噪声加入信号中，得到含噪信号如图2所示。

3.1 降噪效果对比分析

ELMD对含噪信号分解结果如图3所示。K-L散度如图4所示，相似性最低的PF6为余项。

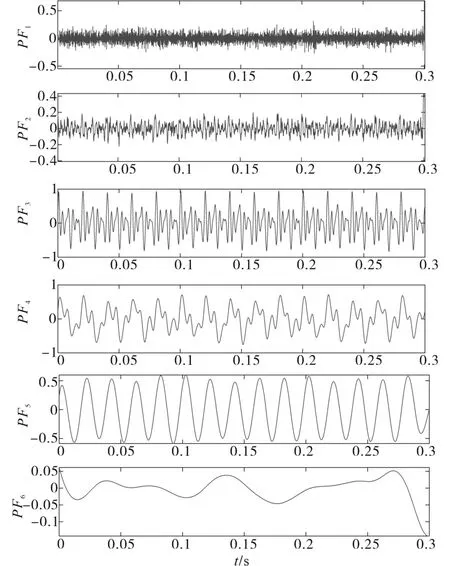
图3 ELMD分解结果Fig.3 Decomposition result of ELMD

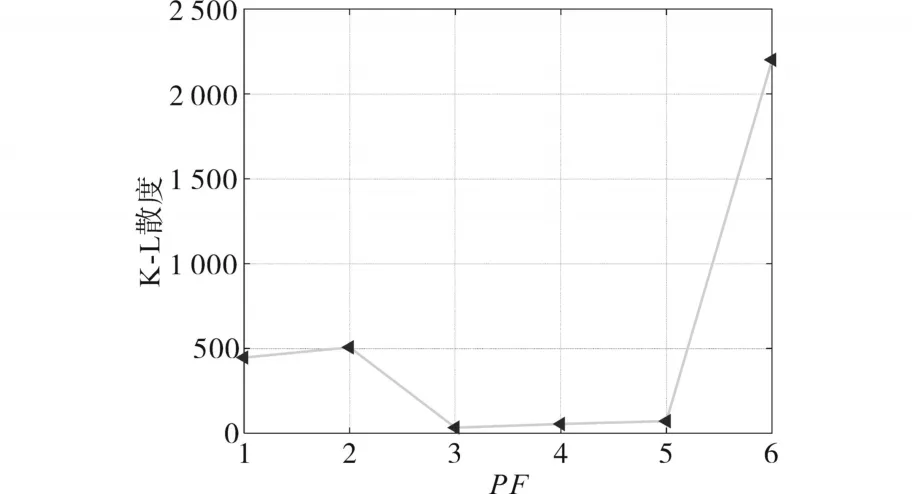
图4 ELMD各PF分量的K-L散度Fig.4 K-L Divergence of ELMD

对PF1～PF5的K-L散度归一化记录于表1，可见PF2为分界分量，此时剔除PF1分量，并对PF2和剩余分量进行SVD二次降噪，降噪重构后波形如图5所示。

表1 各PF与原信号K-L散度归一化值Tab.1 Normalized values of K-L divergence

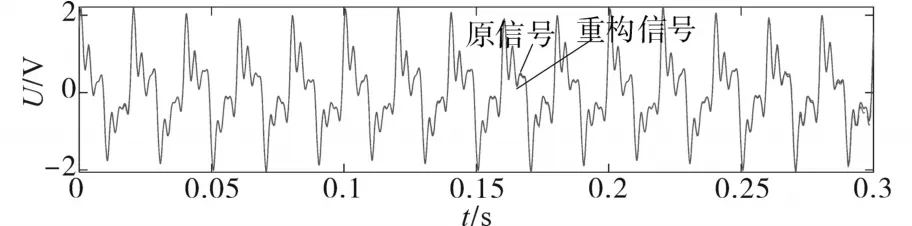
图5 降噪重构波形Fig.5 Noise reduction and reconstruction waveform

由图5波形可以看出，除端点效应造成的端点处有些许误差，重构波形绝大部分与原信号近乎完全贴合，最大程度得保留了信号的原始特征。

为进一步验证文中方法降噪效果，现将文中ELMD-SVD降噪方法与EEMD-SVD降噪方法[16]进行对比。EEMD在EMD基础上使用了白噪声辅助分析，是目前常用的降噪方法，文献[16]将EEMD与SVD结合用于矿山微震信号降噪。

为定量分析降噪效果，引入均方根误差（RMSE）和信噪比（SNR）公式作为评价指标：

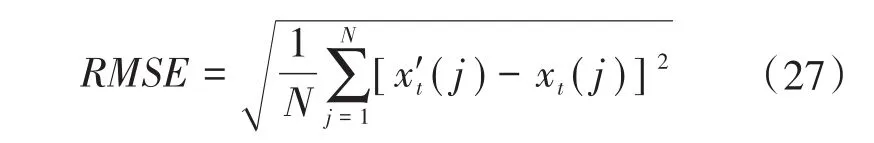
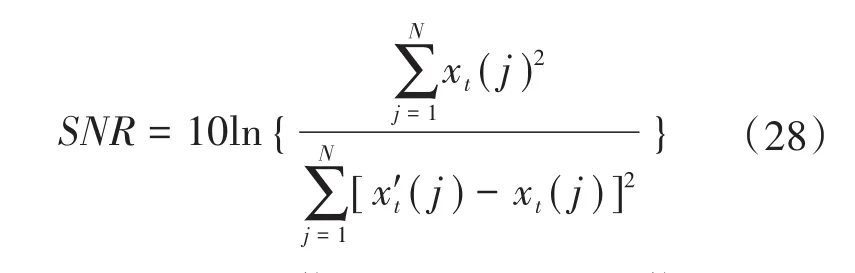
式中：xt（j）为不含噪信号；xt′（j）为含噪信号；N为采样点数。

RMSE越小，SNR越大，说明降噪效果越好。

分别评测上述方法在加入5 dB，10 dB，20 dB高斯白噪声后的降噪表现。

EEMD-SVD方法与文中所提方法的仿真对比结果如表2所示。

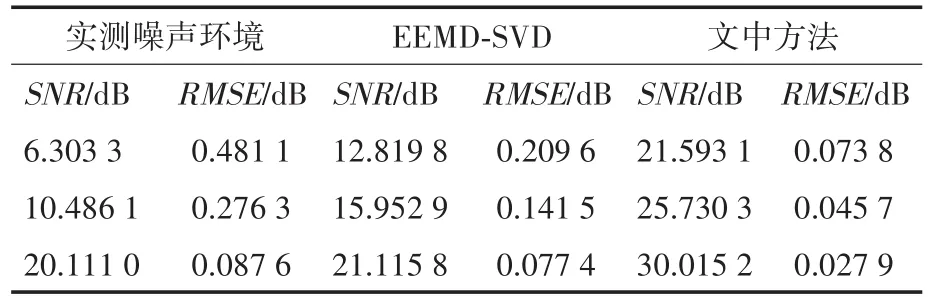
表2 两种方法降噪效果对比Tab.2 Comparison of denoising of two methods

由表2可以看出，在不同噪声环境下，经EEMD-SVD处理后信号SNR提高了1.004 8～6.516 5 dB，RMSE降低了0.010 2～0.271 5 dB；而文中方法SNR提高了9.904 2～15.289 8 dB，RMSE降低了0.059 7～0.407 3 dB。其中在6.303 3 dB的噪声环境下文中方法可实现高达15.289 8 dB的信号恢复能力。表2结果表明文中方法降噪效果更显著且在低信噪比环境下仍具有很强的适应性。

3.2 检测性能对比分析

为验证文中降噪方法对Prony算法检测精度的提升，将式（25）信号分别经EEMD-SVD和ELMD-SVD方法降噪后的信号进行Prony分析。由于高频噪声被剔除，为满足Nyquist采样定理，将两种方法降噪后信号每隔10个采样点取值一次，得到采样频率为1 000 Hz，采样点数为300的信号序列进行Prony分析，Prony阶数设置为12。

EEML-SVD-Prony方法与文中所提方法检测结果对比如表3所示。

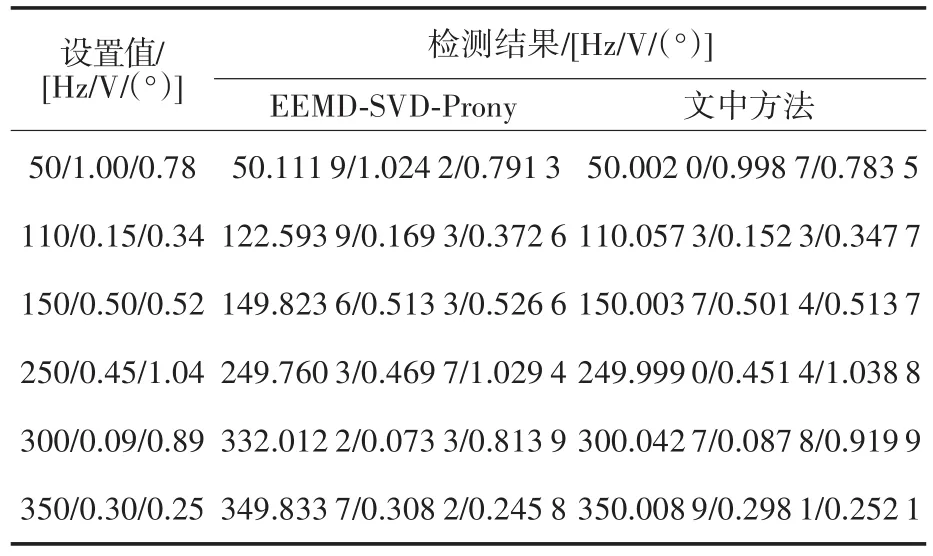
表3 检测结果对比Tab.3 Comparison of test results

由表3数据可见，在20 dB噪声环境下，EEMD-SVD-Prony方法对各整数次谐波拟合较好，但对于幅值含量较低的110 Hz间谐波和300 Hz偶次谐波基本无法准确辨识。而文中方法对于各次谐波间谐波的频率幅值相位均能准确辨识，有效提高了Prony算法的对间谐波的辨识能力。且EEMD需要手动设置分解阶数，而ELMD无需人为干预。

3.3 算法比较

文献[17]提出基于CEEMD和改进Prony的谐波分析方法。

为进一步说明文中所提方法的优越性，采用与文献[17]相同的信号模型，在20 dB噪声环境下，设置ELMD白噪声加噪幅值为0.8，加噪次数为300，SVD分解阶数为8。文中所提方法降噪后的仿真辨识结果与文献[17]方法结果对比如表4～表6所示。

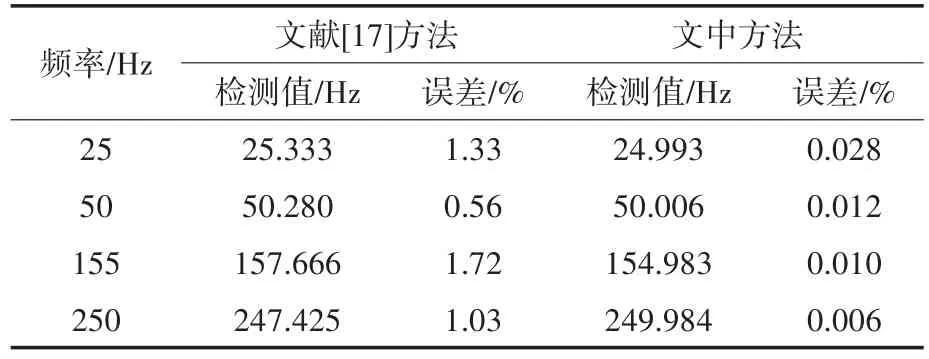
表4 频率检测结果Tab.4 Frequency detection result

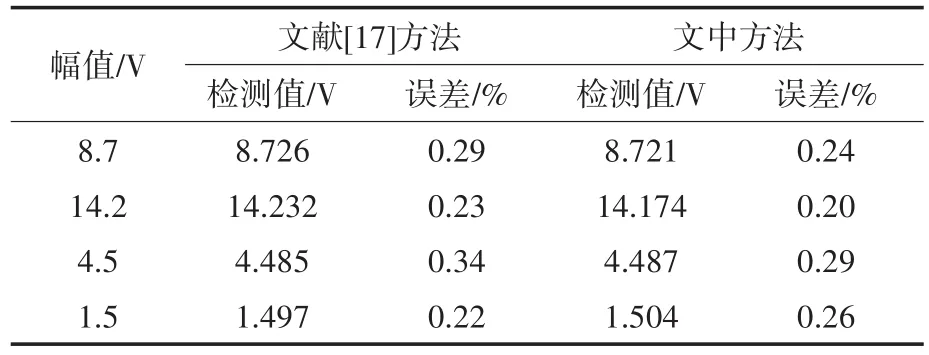
表5 幅值检测结果Tab.5 Amplitude detection results

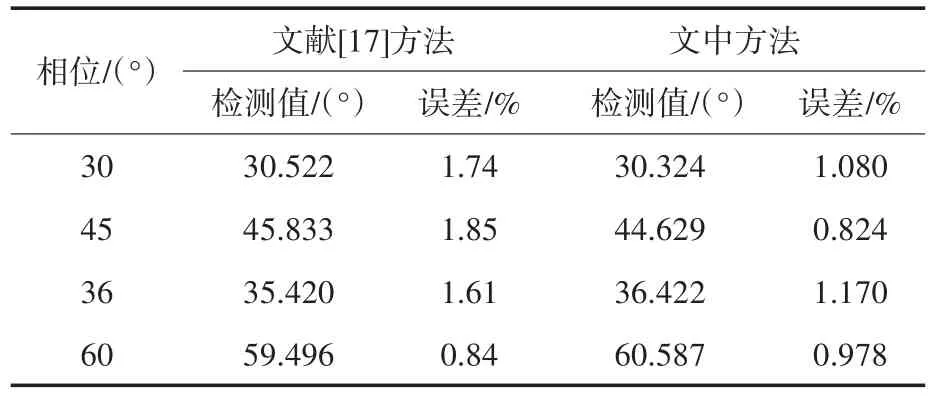
表6 相位检测结果Tab.6 Phase detection results

由表4～表6中数据可见，文中方法频率检测精度更高，对25 Hz和155 Hz间谐波的测量精度达到0.028%和0.01%，比文献[17]方法的频率检测精度高出一个数量级，得益于ELMD的抗模态混叠能力和K-L散度的含噪分量识别，ELMDSVD-Prony方法检测结果更加准确。

3.4 实测信号验证

为更好地验证文中所提方法的有效性，采用文献[18]的实际信号，其为无补偿直流电弧炉的特征信号，由基波（50 Hz）、高次谐波（125 Hz）和间谐波（25 Hz）组成。信号采样频率为10 kHz，采样点数为3 000，在20 dB噪声环境下波形如图6所示。设置ELMD加噪幅值为0.8，加噪次数为300，SVD分解阶数为6，经ELMD-SVD降噪重构后波形如图7所示。

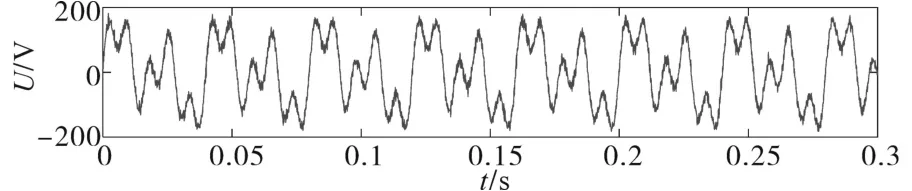
图6 采集信号波形图Fig.6 Acquisition signal waveform

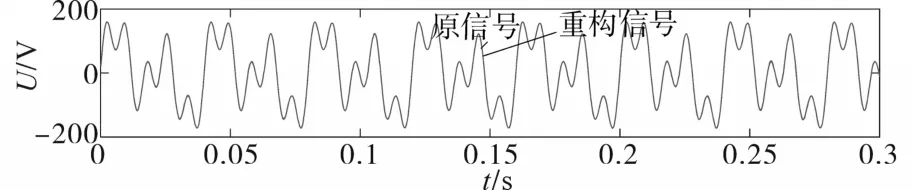
图7 降噪重构信号波形Fig.7 Noise reduction and reconstruction signal waveform

对降噪后信号每隔20采样点取值一次，得到采样频率为500 Hz信号进行Prony分析，参数辨识结果如表7所示。

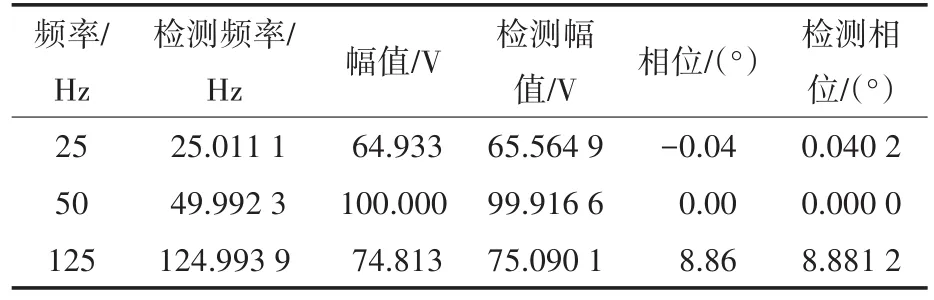
表7 实测信号参数辨识Tab.7 Parameter identification of measured signal

由表7可知，文中算法对实测数据的频率检测精度较好，对25 Hz，50 Hz，125 Hz高次谐波的频率检测误差分别为0.044 4%，0.015 4%，0.004 9%，幅值和相位检测误差均在1%以下。验证了文中方法的有效性。

4 结论

针对噪声干扰电力系统谐波信号提取问题，文中利用ELMD的滤波器组结构对含噪信号进行初步降噪，再利用K-L散度确定有效分量进行SVD二次降噪，最后对去噪后信号进行Prony分析，充分发挥各算法优点。结果表明，文中方法在低信噪比环境下仍具有优异的信号恢复能力和谐波参数辨识能力。