Y源高增益DC-DC变换器滑模控制技术的研究

王凤莲，韦正怡，周明珠，曹益畅，郝杨阳，丁新平

（1.青岛理工大学信息与控制工程学院，山东 青岛 266520；2.南京信息工程大学自动化学院，江苏 南京 210044）

传统Boost变换器在低功率场合具有携带方便、体积小等优点，在大功率场合具有稳定性好、易于控制等优点。但是传统Boost变换器的缺点也非常明显，由于自身升压能力不足，所以在高升压场合，电路容易运行于过高的占空比下，这将导致功率开关管的导通损耗非常大，且控制难度增加；同时开关管和二极管承受的反向电压非常大，导致输出二极管的反向恢复时间和反向恢复损耗加大，使得变换器效率急速下降[1]。由于上述缺点的存在，新型高增益DC-DC电路成为研究的热点[2-4]。

目前工业上对直流变换器的控制方式主要是PID控制，因其控制思路和参数整定相对简单，在工业界备受欢迎[5-6]。但是PID控制需要对模型进行精确建模，在对高阶、复杂的对象建模时较为困难，甚至无法建立精确的传函数学式，影响了PID控制的鲁棒性和响应效果。在上世纪五十年代，滑模控制（sliding-mode control，SMC）技术被首次提出。滑模技术因为具备优良的动态响应性和鲁棒性能得到了广泛的关注[7-9]。

文献[7]针对Boost电路提出了一种基于正交多项式函数逼近的滑模自适应控制策略，针对Buck电路提出了一种基于神经网络逼近的滑模自适应控制器；文献[8]和文献[9]分别针对Boost电路和Buck三电平电路设计了基于PWM调制的滑模变结构控制器；鲜有文献对高阶直流升压电路进行滑模控制研究。

本文提出一种新型带有耦合电感的高增益直流变换器。利用状态空间平均法对变换器建模，然后通过数学软件分析计算电路的小信号模型并求解出电路输出电压关于占空比的传递函数。分别采用PID控制器和滑模控制两种控制方式对电路进行控制，以此对比出加入趋近律的滑模变结构控制对高升压直流变换器有更强的鲁棒性和更快的响应速度。最后利用Simulink工具箱仿真验证了滑模控制的正确性。闭环实验结果验证了滑模变结构控制对高阶直流变换器控制的有效性。

1 Y源DC-DC升压变换器

图1所示为新型高增益耦合电感直流变换器（Fibonacci switch capacitor-Y sources DC-DC converter，FSCYS）的结构原理图。FSCYS由一个直流电源、一个独立电感、一个开关管、两个二极管、三个电容和一个三绕组耦合电感构成。输入电感L1提供连续的输入电流，二极管D1和电容C1组成钳位回路，能够很好地吸收开关管上因漏感产生的电压尖峰。三耦合绕组（N1：N2：N3=1：n1：n2）呈Y型连接，能够最大化提升输出电压增益，电路的增益为

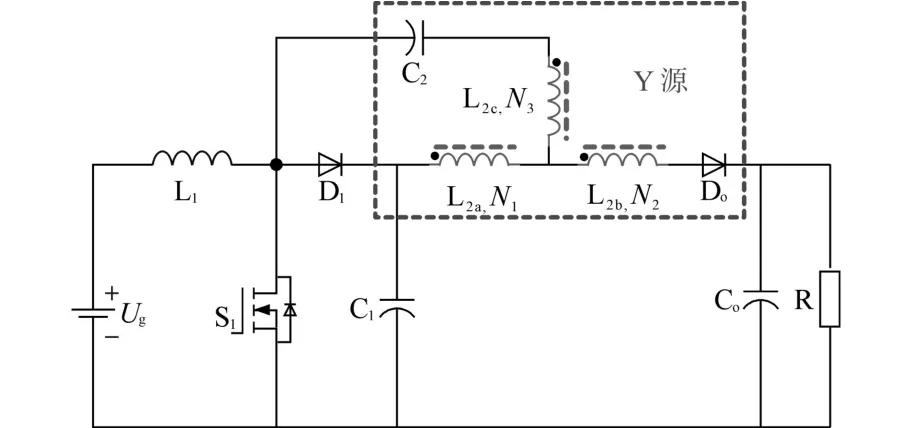
图1 新型高增益耦合电感直流变换器Fig.1 Novel high-gain coupled inductor DC-DC converter

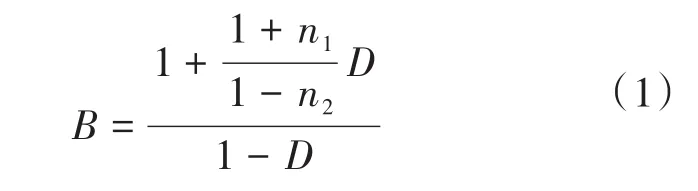
式中：D为直通占空比。

2 Y源DC-DC变换器的建模

3 Y源DC-DC变换器的滑模控制器设计

3.1 滑模控制律推导

为简化控制量的计算过程，不同于在PID控制器中使用双极性三角波为载波，在滑模控制中，将采用单极性的锯齿波为载波来产生PWM，具体实现方案如图2所示。

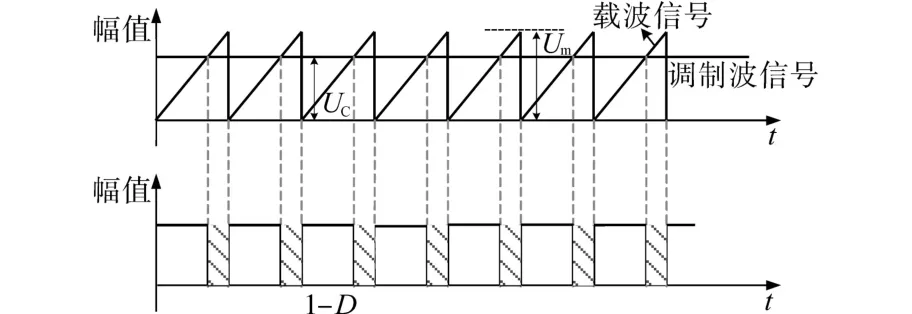
图2 FSCYS滑模控制器PWM调制策略Fig.2 PWM modulation strategy of FSCYS sliding mode controller

从图2可以看到，采取单极性的锯齿波作为载波调制时，根据直流电源的工作需要，在调制信号小于载波信号时，则产生一个低电平，反之，则会有高电平产生。由于式（18）解出的是关于Dˉeq的控制量表达式，所以在仿真和计算中令载波信号的幅值为0～1，频率等同开关管开关频率，则D=（1-滑模控制器产生的调制信号）＜载波信号。

3.2 滑模控制的抖振抑制设计

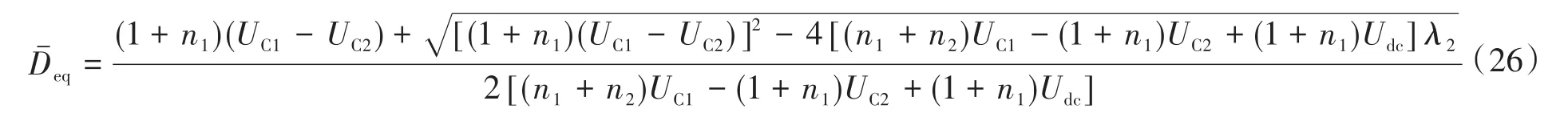
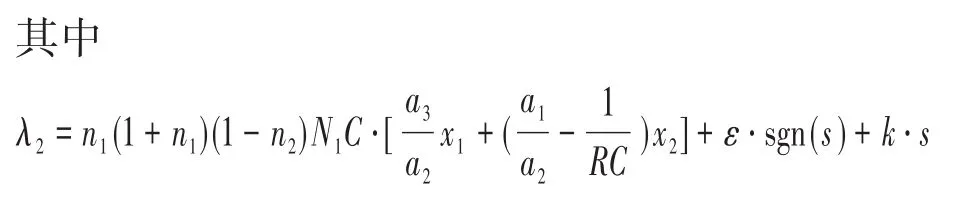
4 仿真对比

图3给出了FSCYS直流电源结构的SMC实现框图，在图3中的比例+微分方框中加入趋近律即为加入趋近律后的SMC实现框图。根据框图在Matlab∕Simulink中搭建仿真图并进行仿真实验。图4、图5、图6所示分别为FSCYS在简单滑模控制、加入等速趋近律后的滑模控制、加入指数趋近律后的滑模控制的输出电压动态响应。通过开关切换，在t=0.4 s时产生10 V的输入电压扰动；在t=0.8 s时，将负载减小为原来的2∕3。从图中可以看出，未加趋近率的输出电压在负载切换时误差较大，经过分析可知是由于滑模控制中的固有问题——抖振。在加入趋近律后，FSCYS的输出效果较好，没有明显的干扰现象，且过渡过程平滑、稳定。与加入等速型趋近律相比，指数型趋近律的加入极大地优化了FSCYS的动态过程，加入指数型趋近律后，SMC从扰动开始至到达稳态的控制时间仅仅为6 ms，这对于要求快速响应的高增益直流变换器具有重要意义。

图3 FSCYS直流电源结构的SMC实现框图Fig.3 SMC realization block diagram of FSCYS DC power supply structure

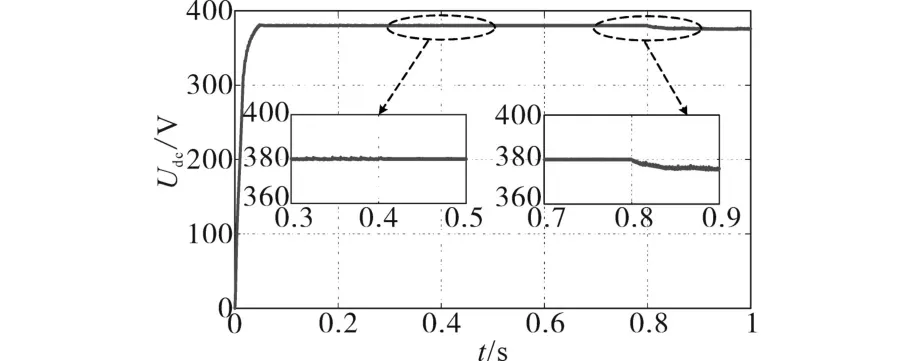
图4 未加趋近律的输出电压的动态响应Fig.4 Dynamic response of output voltage without reaching law

图5 加入等速趋近律后FSCYS的输出动态响应图Fig.5 The output dynamic response graph of FSCYS after adding the isokinetic reaching law

将闭环方式下的FSCYS输出响应性能进行对比，传统PID控制、无趋近律的滑模控制、等速趋近律的滑模控制和指数趋近律的滑模控制的超调量分别为192%，0.31%，0.23%，0.21%，可以看出滑模控制的超调量特别小。

5 实验

图7、图8、图9分别为FSCYS在PID控制、简单滑模控制、加入指数趋近律的滑模控制作用下的动态响应波形图。

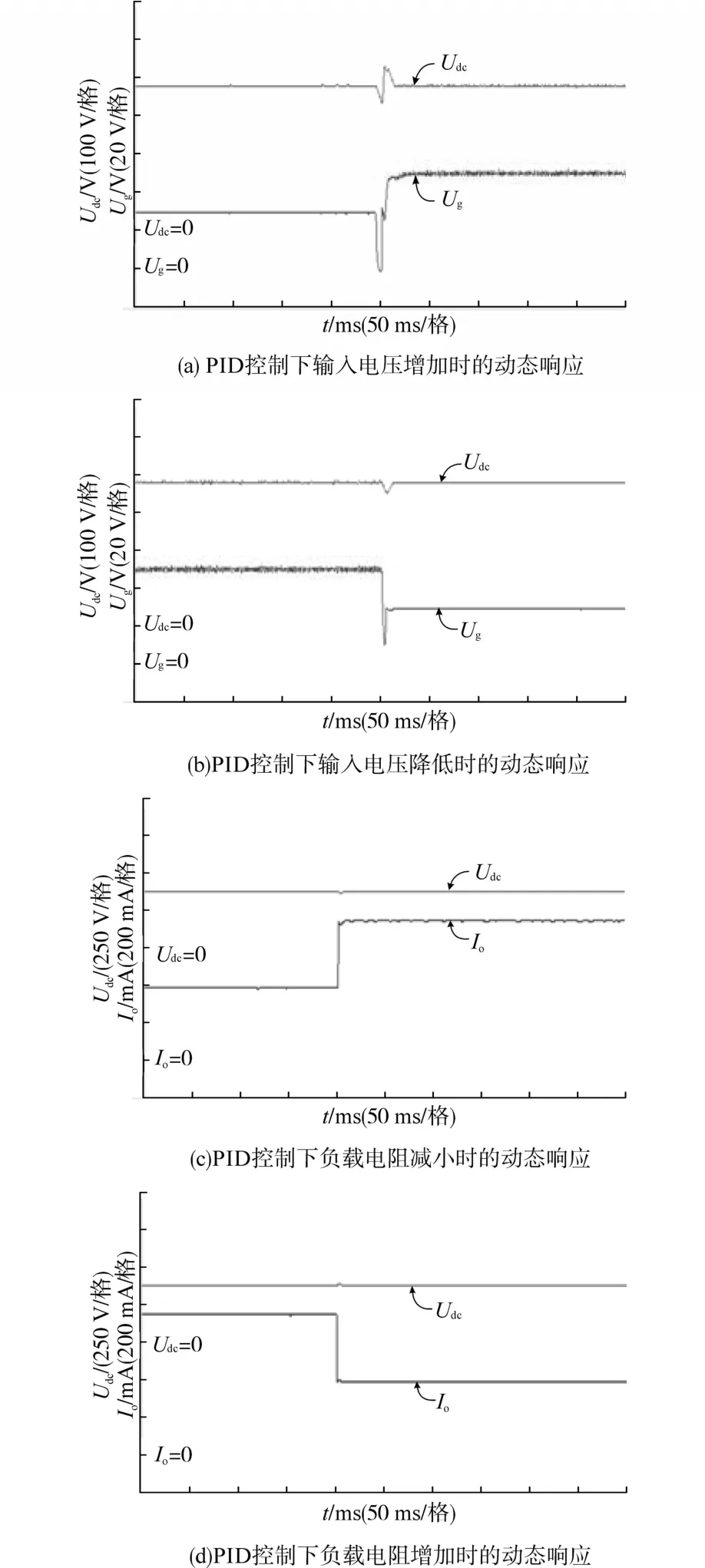
图7 PID控制器下的FSCYS的动态响应Fig.7 Dynamic response of FSCYS under PID controller

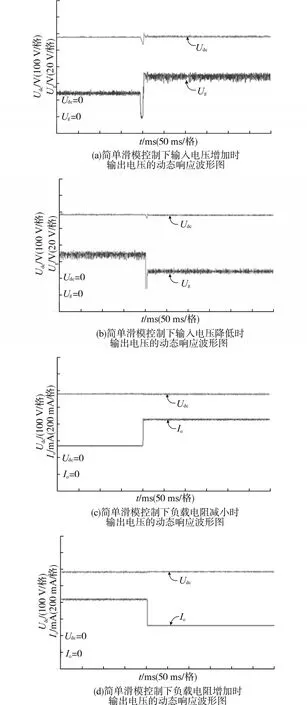
图8 简单滑模控制器下FSCYS的输出电压动态响应波形图Fig.8 The output voltage dynamic response waveforms of FSCYS under simple sliding mode controller

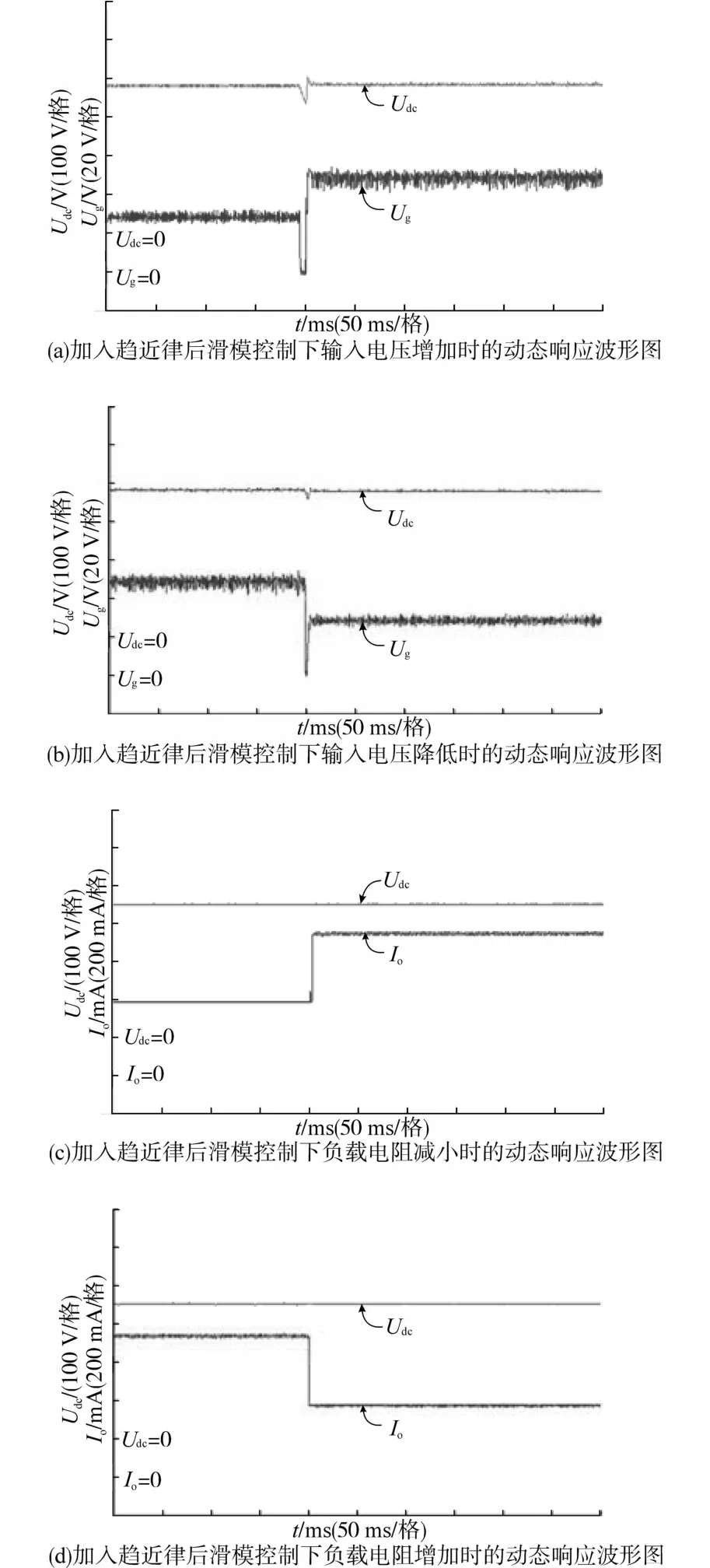
图9 加入趋近律后滑模控制器下FSCYS的动态响应波形图Fig.9 The dynamic response waveforms of FSCYS under sliding mode controller with reaching law added

在设计所提变换器的PID控制器参数时，采用小信号建模方法，利用Bode图补偿进行PID参数的校正[12]，并借助Matlab的Sisotool工具箱得到PID 控制器参数为：Kp=0.833 8，Ki=83.176，Kd=0.000 020 081 1。

图7a、图8a、图9a为输入电压从30 V突变到50 V时的动态响应波形图；图7b、图8b、图9b为输入电压从50 V下降到30 V时的动态响应波形图；图7c、图8c、图9c为负载从720 Ω突变到360 Ω时的动态响应波形图；图7d、图8d、图9d为负载从360 Ω突变到720 Ω时的动态响应波形图。

图7a可以看到，输出电压在经过大约20 ms左右的时间达到新的稳态，从图中基本上看不到输出电压的稳态误差。由于在升压过程中是两个输入电源的串联，输入电压纹波增加，导致输出电压的纹波也有一定的影响。图7b可以看到输出电压的动态品质比升压时的动态品质好。从图7c和图7d可以分析出，负载波动对输出电压没有产生较大的影响，过渡时间大约只有几ms。

图8a中可以看到，输出电压的调节时间明显小于传统的PID控制器，仅仅需要5 ms左右的时间即可稳定，但输出电压有微小的稳态误差和相对较大的输出电压纹波，这和理论分析时滑模控制器的固有缺陷有关。从图8c、图8d可以明显的看出，当负载扰动时，输出电压基本上没有明显的变化，只是在纹波上有非常微小的变化，这也是滑模变结构控制相比于传统PID控制器的优势。

在简单滑模控制中加入指数趋近律后，FSCYS电路的输入输出动态响应如图9所示。理论分析时，加入趋近律的滑模控制可以减小输出电压的抖振现象和加快响应速度，这一点在图9a和图9b中得到了验证，在同样的扰动下，加入趋近律后输出电压的纹波相对较小，响应速度相对较快。

图10所示为实验样机图，主要由供电电源、驱动电路、Y源电路、采样电路、负载、示波器和软件控制平台构成。

图10 FSCYS变换器样机Fig.10 FSCYS converter prototype

6 结论

本文对FSCYS采用滑模控制器进行闭环控制，滑模控制器比PID控制响应速度更快、超调量更小。分别设计了无趋近律的滑模控制、等速趋近律滑模控制、指数趋近律滑模控制三种控制器。仿真和实验表明指数趋近律滑模控制和等速趋近律滑模控制能够有效解决无趋近律的滑模控制的抖振问题；指数趋近律滑模控制相较于等速趋近律滑模控制响应速度更快、稳定性更好；滑模控制非常适合应用于高阶直流变换器领域。