基于CSO-SVM的数控机床主轴热误差建模

刘洪江，胡 腾,2，何 勇，董 峰，罗 为

（1.西南石油大学机电工程学院，四川 成都 610500；2.四川普什宁江机床有限公司，四川 都江堰 611830；3.中国石油集团川庆钻探工程有限公司培训中心，四川 成都 610213；4.成都广通汽车有限公司，四川 成都 611430；5.中国质量认证中心，四川 成都 610065）

近年来，随着精密加工技术的不断进步，制造行业对数控机床的加工精度提出了更高的要求。热误差占数控机床总加工误差的40% 以上，是影响数控机床加工精度的关键因素[1-3]。主轴是数控机床最重要的部件之一，因此对主轴热误差的研究尤为重要。目前，主要采用误差防止法和误差补偿法来减小主轴热误差[4]。误差防止法的本质是抑制或消除热误差，如通过优化数控机床结构、控制环境温度等方式减少主要热源产热，但是会极大地增加机床设计和制造的成本，故在工程中应用较少[5-6]。误差补偿法是通过构建机床温度变化与主轴热误差的映射关系，由主轴的温度变化来预测主轴热误差，并通过数控系统对热误差进行补偿[7-9]。该方法成本低、实用性好、预测的精度稳定，在实际工程中被广泛应用。

对于误差补偿法，构建精度高、鲁棒性好的热误差预测模型（以下简称热误差模型）是实现热误差补偿的重要前提[10-11]。许多学者对热误差模型进行了深入研究。王维等[12]采用线性回归分析法建立了热误差模型。考虑到离散的温度变量不能准确反映整个机床温度场的变化，且温度变量与热误差之间会逐渐呈现极强的非线性关系，采用线性回归分析法建模会出现一定的偏差，所以人工神经网络和机器学习被大量应用到热误差建模。谭峰等[13]通过建立集成BP（back propagation，反向传播）神经网络模型来处理温度变量与热误差之间的非线性关系，并取得了良好的预测精度。Li等[14]采用粒子群优化（particle swarm optimization,PSO）算法有效优化了BP神经网络的拓扑结构，从而进一步提高了BP神经网络模型的预测精度。Qiang等[15]将灰色关联理论应用于热误差建模，以解决温度数据样本量少、信息贫乏的问题。朱星星等[16]以进给轴为研究对象，建立了基于最小二乘支持向量机（support vector machine,SVM）的热误差模型，取得了比较理想的补偿效果。然而，以上方法都存在局限性：神经网络模型对数据样本量的需求高且收敛速度慢，在建模时，只有选择了合适的拓扑结构，才可能取得好的预测效果：SVM算法可以通过小样本数据建模，并且克服了局部收敛的问题，但预测精度对参数的选择非常敏感；PSO算法可以对神经网络模型的拓扑结构进行优化，也可以对SVM的关键参数寻优，但存在收敛速度慢、局部寻优能力较差等问题，对预测精度有较大影响。

为了解决上述问题，笔者首先采用五点法测量某数控机床主轴的热误差；其次，利用鸡群算法全局搜索能力强、搜索效率高等优点，对SVM模型的惩罚参数c和核参数g进行优化，实现鸡群优化算法（chicken swarm optimization,CSO）算法与SVM的结合，即建立基于CSO的SVM热误差模型；最后，为了验证所建模型的预测精度及鲁棒性，将该模型与多元线性回归模型和PSO-SVM模型的预测精度进行对比，并改变工况对该模型的鲁棒性进行验证。

1 主轴温度和热误差的测量

1.1 五点法测量原理

五点法测量如图1所示。主轴前端装夹了1根测试芯棒，5个位移传感器（S1至S5）的相对位置固定。其中，S3位于芯棒中轴线方向，S1与S2以及S4与S5均沿芯棒径向布置，S1、S4用来测量主轴X向的热误差，S2、S5用来测量主轴Y向的热误差。

图1 五点法测量示意Fig.1 Schematic of five-point measurement

五点法测量的原理如图2所示。由于偏转角θx较小，则θx≈tanθx，即主轴Z向的热误差E和X向的热漂移误差θx分别为[17]：

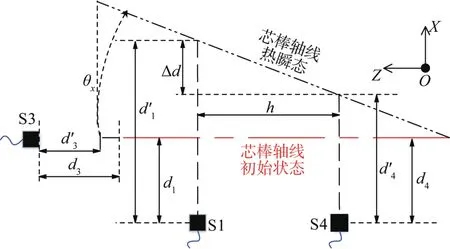
图2 五点法测量原理示意Fig.2 Schematic of principle of five-point measurement

式中：d3、d3′分别为初始状态和热瞬态下S3传感器探头与测试芯棒前端面的距离；d1、d1′分别为初始状态和热瞬态下S1传感器探头到芯棒轴线的距离；d4、d4′分别为初始状态和热瞬态下S4传感器探头到芯棒轴线的距离；h为同侧传感器S4与S1之间的距离。

1.2 主轴温度和热误差的测量方法及测量结果

大量研究表明，在主轴达到热平衡的过程中，主轴轴向热误差相比其他方向的热误差更显著，所以选取主轴轴向热误差为主要研究对象，并在某数控机床进行温度和主轴热误差的测量实验。实验按照ISO230-3-2007中数控机床热误差的测量标准，采用五点法测量。选用电涡流位移传感器采集热误差数据，选取PT100热电偶温度传感器采集温度数据。

传感器探头与测试芯棒端面或法面的距离均保持为1 mm。为了准确反映机床温度场的变化，根据文献[18]提出的温度传感器布置方案及温度测点优化方案得到了4个关键温度测点，如表1所示。接着在机床的该4个测点布置好温度传感器，如图3所示。

表1 机床的关键温度测点Table 1 Key temperature measuring points of machine tool

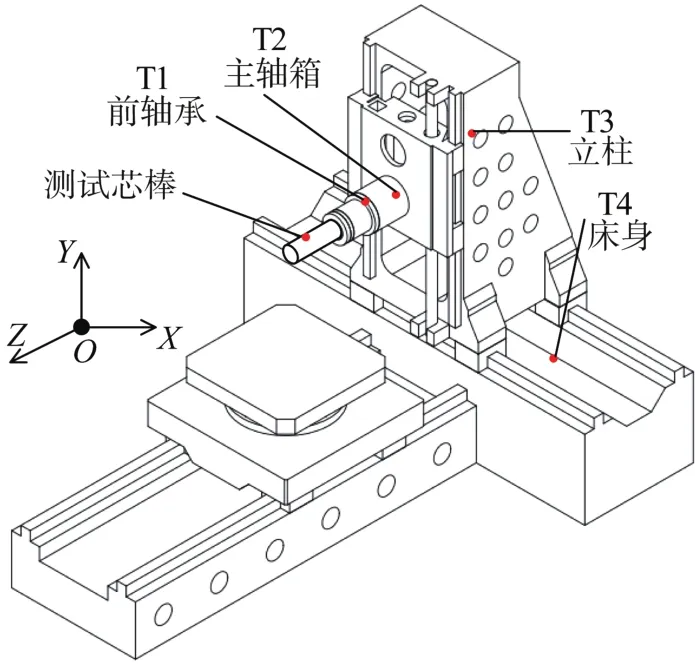
图3 机床关键温度测点的分布Fig.3 Distribution of key temperature measuring points of machine tool

机床温度和主轴热误差的测量平台如图4所示。主轴以3 000 r/min的恒定转速保持空转，每隔3 min同步采集一次温度数据和热误差数据。实验进行3 h，共采集到60组数据。

图4 机床温度和主轴热误差的测量平台Fig.4 Measuring platform of machine tool temperature and spindle thermal error

待机床完全冷却后，再设置主轴转速分别为2 000 r/min和4 000 r/min进行实验，并将采集到的数据进行简要分析。

当转速为3 000 r/min时机床各关键测点的温度变化曲线如图5所示。由图可知，3 h后各测点温度基本不再变化，即主轴已经达到热平衡。

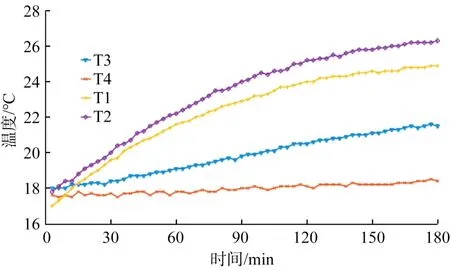
图5 转速为3 000 r/min时机床各关键测点的温度变化曲线Fig.5 Temperature variation curve of key measuring points of machine tool at rotate speed of 3 000 r/min

不同转速下主轴热误差变化曲线如图6所示。由图可知，在不同的转速下，主轴热误差不同。所以研究变工况下热误差模型的鲁棒性必不可少。

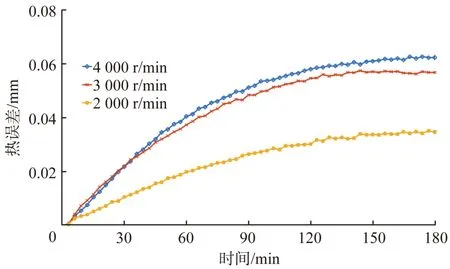
图6 不同转速下主轴热误差变化曲线Fig.6 Variation curve of spindle thermal error at different rotate speeds

2 基于CSO算法的SVM热误差建模

2.1 SVM热误差建模

多元线性回归建模是较常见的机床主轴热误差建模方法。该建模方法通常需要大量实验数据来构造超越方程，其求解过程较为繁琐，计算收敛性较差，且可能不收敛。SVM是一种人工智能技术和机器学习方法，目前在模式识别、信号处理、回归预测等领域得到了大量应用。与神经网络相比，SVM能解决训练时间长和训练样本量大带来的问题，并有较强的处理非线性映射问题和全局寻优的能力[19]。该方法的理论支撑源于结构风险最小化原则，通过选择函数子集及其判断函数，最终使风险达到最小。

2.2 CSO算法

为了提升SVM模型的预测精度，常常采用遗传算法、粒子群算法等对SVM的重要参数进行寻优。然而遗传算法和粒子群算法容易出现收敛早且局部搜索能力差的问题，容易陷入局部最小值。

CSO算法是一种新颖的仿生群体智能算法，通过模拟具有等级秩序的鸡群觅食行为达到全局优化的效果[20]。CSO算法根据适应度值的大小将鸡群分为多组，适应度值较小的几个被判别为公鸡，较大的几个判别为小鸡，其余则为母鸡。每组包括1只公鸡、若干母鸡和若干小鸡。鸡群跟随公鸡觅食，小鸡在母鸡周围觅食，觅食能力从强到弱依次为公鸡、母鸡、小鸡。在这种等级秩序下，不同鸡群间相互合作，协同觅食，且依据各自的运动规律不断更新位置以达到搜索食物的目的，直至寻找到最佳觅食位置。这种觅食方式不仅提升了算法的局部优化能力，其全局优化能力也得到了提升。

CSO算法的流程如图7所示。

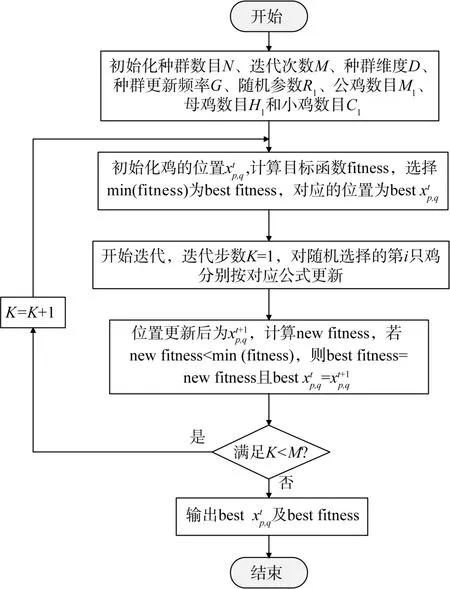
图7 CSO算法流程Fig.7 CSO algorithm flow

2.3 SVM热误差模型的优化

SVM热误差模型的惩罚参数c和核参数g对SVM模型预测精度的影响较大。为了提高SVM模型的预测精度，采用CSO算法来优化c和g，即将CSO算法与SVM结合进行建模。把c和g的初始值作为CSO算法中鸡群的初始位置，将SVM模型的均方根误差MSE作为CSO算法中的适应度函数，即：

式中：yv为实际测量值；y＇v为模型预测值；n为样本数量。

f（x）值越小，表示预测精度越高。根据CSO算法中鸡群的运动规律，不断迭代更新鸡群的位置，直至输出最小的适应度值和对应的最优参数c和g，即完成了CSO算法与SVM的结合，建立了基于CSOSVM的热误差模型。

3 CSO-SVM模型的预测精度及鲁棒性验证

3.1 不同模型预测精度的对比

构建CSO-SVM模型后，将主轴转速为3000r/min时机床各关键温度测点的温度时序数据作为模型的输入，输出热误差。其中，随机选取45组数据作为训练集进行训练，训练完成后，将余下的15组数据作为测试集进行验证。CSO-SVM模型训练结果和测试结果如图8所示。可以得到CSO-SVM模型的均方根误差（即最佳适应度值）为0.002 404，计算出相应的最佳参数c和g分别为7.346 5和0.026 1。同时，得到训练集的残差为-2.9～2.9 μm，测试集的残差为-1.2～2.5 μm。

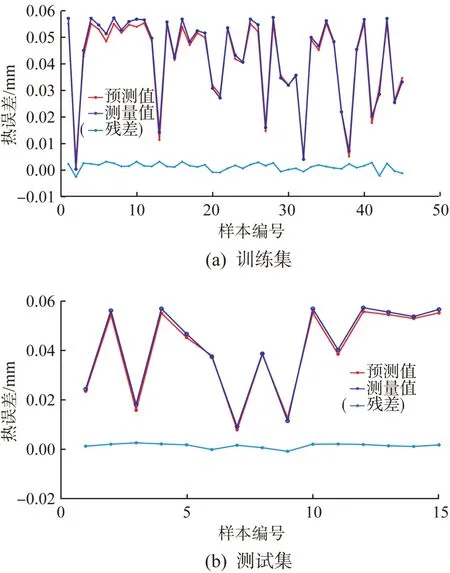
图8 转速为3 000 r/min时CSO-SVM模型的热误差预测结果Fig.8 Thermal error prediction results of CSO-SVM model at rotate speed of 3 000 r/min

为了进一步验证CSO-SVM模型的优越性，基于转速为3 000 r/min时的实验数据，将其预测结果与多元线性回归模型、PSO-SVM模型的预测结果进行对比，结果如图9所示。由图可知，CSO-SVM模型的平均预测精度高达97.32% ，相比于多元线性回归模型和PSO-SVM模型分别提升了6.53% 和4.68% 。

图9 不同模型预测精度的对比Fig.9 Comparison of prediction accuracy of different models

3.2 CSO-SVM模型鲁棒性验证

在实际工程中，工况在不断变化。为了验证CSO-SVM模型的鲁棒性，体现其实际工程价值，基于转速为2 000，4 000 r/min时的实验数据进行CSOSVM模型热误差预测分析。预测结果如图10所示。由图可知，在2 000，4 000 r/min的主轴转速下，模型残差分别为-5.3～2.8 μm、-3.3～3.1 μm，平均预测精度分别达到了92.53% 和91.82% 。

图10 不同工况下CSO-SVM模型的热误差预测结果Fig.10 Thermal error prediction results of CSO-SVM model under different working conditions

此外，当转速为3 000 r/min时对主轴径向热漂移误差进行预测分析。预测结果如图11所示。由图可知，其残差为-7.516 5×10-4°～7.500 0×10-4°，预测精度高达91.76% 。

图11 转速为3 000 r/min时CSO-SVM模型的主轴径向热漂移误差预测结果Fig.11 Prediction result of spindle radial thermal drift error of CSO-SVM model at rotate speed of 3 000 r/min

研究表明：所建CSO-SVM模型具有较高的预测精度和良好的鲁棒性，在实际工程中具有较强的应用价值。

4 结论

1）当主轴转速为3 000 r/min时，CSO-SVM模型训练集和测试集的残差分别达到了-2.9～2.9 μm、-1.2～2.5 μm，其平均预测精度高达97.32% 。相比于传统的多元线性回归模型和PSO-SVM模型，平均预测精度分别提升了6.53% 和4.68% ，体现了CSO算法与SVM结合的优越性。

2）当主轴转速为 2 000，4 000 r/min时，CSOSVM模型热误差的平均预测精度分别为92.53% 、91.82% 。当主轴转速为3 000 r/min时，CSO-SVM模型主轴径向热漂移误差的平均预测精度达到91.76% 。可见CSO-SVM模型具有良好的热误差预测能力和鲁棒性，拥有较强的实用性和工程应用价值。