基于空变分离的两步聚焦双基曲线合成孔径雷达成像

徐熙毅，谭鸽伟，李彪

(华侨大学 信息科学与工程学院，福建 厦门 361000)

0 引言

随着雷达成像技术的发展，合成孔径雷达(SAR)平台的运动方式也呈现出多样化。其中，曲线运动轨迹双基SAR系统因其特殊的应用价值引起关注，它可通过调整雷达的运动轨迹和波束指向，直接获得重要区域的二维高分辨图像和散射信息，实现精确定位。

由于收发平台分置，曲线轨迹双基SAR的斜距历程是两个双曲方程之和，其回波频谱不能直接用驻留相位原理来获得。此外，由于收发平台具有不同的三维速度和三维加速度，使回波信号距离- 方位的耦合更加复杂，并带来更加严重的二维空变性，给曲线双基SAR的成像处理带来了困难。

基于双基SAR成像所提出的算法，主要分为时域算法和频域算法。时域算法主要有反向投影(BP)算法，BP算法能够为复杂的飞行轨迹问题提供解决方案。通过距离误差补偿，理论上可以实现任意配置下的精确成像。然而，BP算法的计算效率低，不适合实际应用。文献[5-8]提出了快速BP算法及其改进形式，来加速成像过程。以上方法消除了冗余的相位误差计算，在一定程度上提高了计算效率。然而，计算时间的成本仍然大于频域算法。文献[9-10]给出了双基SAR的距离多普勒(RD)算法，但是都没有考虑曲线轨迹和非等速平台带来的二维空变问题，不适用于曲线运动轨迹下的双基SAR成像。而改进的RD算法虽然考虑了距离向的空变问题，但是忽略了方位向的空变性，当成像场景变大时会出现严重的散焦现象。文献[14-17]提出了线性调频变标(CS)算法及其改进算法，但该类算法只考虑了一次项的空变补偿，忽略了高次项的空变误差影响。扩展的方位非线性调频变标(EANLCS)算法较好地解决了方位向的空变问题，但是没有考虑距离向空变相位误差和加速度的影响，适用场景有限。文献[23-25]通过在距离向引入Keystone变换，方位向运用EANLCS算法解决二维空变问题，然而该类算法推导过程复杂，而且只补偿了多普勒偏移和多普勒调频率的空变误差，忽略了高阶项的空变影响，不适用于大场景模式。

综上所述，现有算法不能有效解决曲线运动给双基SAR带来的更复杂的二维耦合问题和更加严重的二维空变问题。为此，本文提出两步聚焦处理方法。首先建立空变分离的斜距等效模型，基于该斜距对回波相位进行空变分离，然后通过参考点匹配滤波直接补偿其非空变部分，完成粗聚焦。对于剩余的空变相位，在距离向通过引入Keystone变换，在方位向通过对多普勒参数进行最小二乘拟合和方位重采样，有效补偿了回波相位的空变误差，从而实现精确聚焦。通过两步聚焦处理显著提高了边缘点的成像性能，适用场景更大，成像深度更广。

1 空变分离的斜距等效模型

如图1所示，以场景中心为坐标原点建立三维直角坐标系，(,,0)为成像区域内的任一点，为方位向时间，当=0时，发射机和接收机的初始位置分别为(,,)和(,,)，然后它们分别以三维速度(t,t,t)、(r,r,r)和三维加速度(t,t,t)、(r,r,r)沿曲线轨迹飞行，()和()分别为发射机和接收机到点的瞬时斜距。

图1 曲线轨迹双基SAR成像几何模型Fig.1 Geometric model of the imaging of bistatic SAR with curvilinear trajectory

设和分别表示发射机和接收机与点目标的初始斜距。依据运动方程，有

(1)

将斜距重新整理为

(2)

式中：

t为发射机斜距的第阶泰勒展开系数，r为接收机斜距的第阶泰勒展开系数，=1,2,3,4。

则点目标到发射机和接收机的瞬时斜距总和为

()=()+()

(3)

将(2)式在=0处进行泰勒展开，可得

(4)

当发射机和接收机沿曲线轨迹飞行时，成像区域内不同位置点目标的斜距历程不同，会引起回波信号的相位空变，从而导致场景边缘点成像效果变差。为了提高聚焦效果，需要分析回波信号的空变性，由三维同性原理，将斜距模型分为两部分：一部分为与点目标位置(,)有关的项，即空变部分；另一部分为与点目标位置无关的项，即非空变部分，故斜距模型中的各阶泰勒展开系数可表示为

(5)

式中：t为发射机斜距的非空变泰勒展开系数；t为发射机斜距的空变泰勒展开系数；r为接收机斜距的非空变泰勒展开系数；r为接收机斜距的空变泰勒展开系数。简化为=+。其中，为场景中心斜距的泰勒系数，=t+r，即非空变部分；与目标位置有关，表示空变部分，=t+r。

故最终的空变分离斜距等效模型为

(6)

为验证本文所提空变分离的斜距等效模型的精确性，采用表1所示参数，对(6)式与原始斜距的误差以及由斜距误差产生的多普勒相位误差进行仿真，如图2所示。

表1 仿真参数Tab.1 Simulation parameters

图2 斜距误差和多普勒相位误差比较Fig.2 Comparison of sloping error and Doppler phase error

假设发射机发射线性调频(LFM)信号，则从目标接收的回波解调到基带后为

(7)

式中：为快时间变量；为光速；和分别为距离向和方位向的时域包络；为发射信号的调频率；为载波波长。

2 第1步粗聚焦—非空变相位补偿

根据驻留相位原理对回波信号进行距离向快速傅里叶变换(FFT)，得到

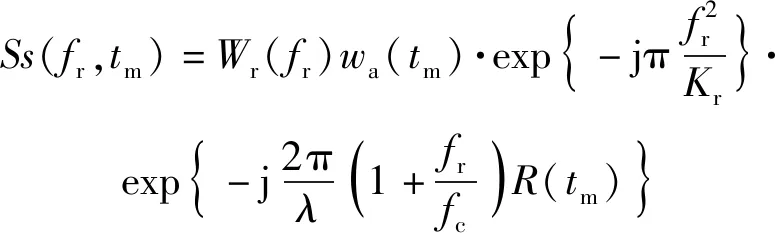
(8)

式中：为距离向的频域包络；为距离向的频率变量；为载波频率。

(8)式中的第2个指数项包含距离徙动项，与目标位置有关的空变项以及三维加速度带来的相位误差项。其中，距离徙动项是距离- 方位的强耦合项，对成像影响较大。而点目标位置(,)的变化会带来严重的空变误差，导致成像效果变差。针对此问题，有必要进行相应处理和补偿。

为分析点目标位置变化带来的空变性，以场景中心为参考点构造补偿函数并进行距离压缩，补偿函数为

(9)

(9)式中各项主要起到以下作用：

1)关于方位时间的1次项，其主要作用是进行线性距离走动(LRCM)矫正，以减小距离- 方位的耦合。

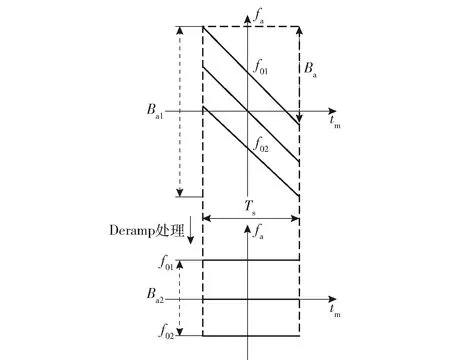
图3 Deramp原理图Fig.3 Schematic diagram of Deramp

3)方位时间的高次项(3次及以上)，其作用主要是补偿高阶非空变相位。

通过以上分析，补偿函数能够同时完成距离走动矫正，距离压缩，方位向Deramp处理以及高次非空变相位补偿，实现点目标的粗聚焦。将(9)式乘以(8)式，得

(10)

由(10)式可知，非空变相位补偿后的剩余项全部为空变相位，包括剩余距离走动项以及Deramp后的残留误差。采用表1所示参数对剩余空变相位进行仿真，如图4所示。由图4可见：场景中心(0 m，0 m)的空变相位误差为0 dB，近点目标位置(200 m，200 m)的空变相位误差为773 dB，边缘点(400 m，400 m)处空变相位误差为1556 dB，表明偏离中心点越远，空变相位误差越大；当成像场景较大时，该空变误差不仅影响距离向聚焦性能，更会严重影响方位向的聚焦效果。

图4 不同点目标处的空变相位误差Fig.4 Space variant phase error at different point targets

这种误差的空变性给误差补偿处理带来了极大的挑战，现有方法大多难以兼顾补偿精度和计算效率。为此，本文提出第2步精确聚焦处理，在距离向引入Keystone变换来消除距离向的主要空变误差，在方位向基于最小二乘拟合推导各阶多普勒参数的线性表达式，并通过方位重采样来解决方位相位的空变性。

3 第2步精确聚焦—空变相位补偿

3.1 基于Keystone变换的距离向处理

由(10)式可知，距离走动矫正完之后还剩余和的一次耦合项1=-1，这是空变距离徙动的主要分量，将通过Keystone变换的方法进行去除。

为了消除剩余的LRCM，令

(11)

式中：为新的方位时间变量。将(11)式代入(10)式，并在=0处进行泰勒展开，整理得

(12)

式中：为带有空变性的方位相位；为剩余距离徙动空变相位；为2次距离压缩空变相位；为剩余高次耦合空变相位。

由(12)式可知，Keystone变换后距离向的1阶空变分量1被完全祛除，只剩下较小的高阶分量。为了分析距离向的空变剩余误差，采用表1所示参数对剩余的各阶相位进行仿真，如图5所示。

图5 距离向剩余空变相位Fig.5 Range to residual space phase

(,)=exp{(++)}

(13)

(13)式与(12)式相乘并作距离向逆IFFT，得到

(14)

式中：Δ=-t-r，t和r分别表示发射机和接收机相对于场景中心的初始斜距。至此距离向处理完成，解决了距离向相位关于目标位置(,)的空变问题。

3.2 基于最小二乘直线拟合的方位重采样处理

根据(14)式，方位向相位具体表示为

(15)

因为为常数，对成像没有影响，故可忽略不作分析。

(15)式包含了与目标位置(,)有关的空变相位。如果不做空变补偿，则不仅会影响成像效果，还会影响成像场景的深度。

由于曲线运动双基SAR收发平台以不同的速度和加速度飞行，方位向无法明确定义，因此不再适合用目标的方位初始时刻来表示双基曲线SAR的方位空变性，而采用频率位置来描述方位空变性。因此，令

(16)

方位相位(15)式可重写为

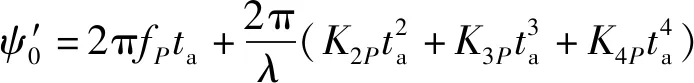
(17)

由构建方位多普勒参数的空变函数为

(18)

(18)式的系数0和1(=2,3,4)通过最小二乘法直线拟合原理求解得到。本文算法采用个点目标来拟合各阶多普勒参数的线性表达式方法如下。

根据(18)式，0，1为待求解项，令=[0,1]已知，

(19)

式中：1,2,3,…,是依据(16)式计算得到的个点目标的频率位置；1,2,3,…,是依据(5)式得到的个点目标第阶空变泰勒系数。

用矩阵形式表达为=，其中：

(20)

(21)

因为(21)式左边各部分均已知，所以可直接求解得到直线的方程系数向量，即最终可得到(18)式中的系数0,1,=2,3,4的具体值。

故信号可重写为

(22)

式中：由于0与无关，代表多普勒参数的非空变项，可直接补偿，补偿函数为

(23)

(23)式与(22)式相乘后，得到信号为

(24)

通过(24)式可以发现，方位相位已经在时域通过线性化了。接着可以通过方位重采样处理祛除剩余的与有关的空变分量，可通过方位向sin插值实现上述操作。采样因子为

(25)

最后通过方位向FFT实现频域聚焦，聚焦信号表达式为

(26)

通过以上分析，绘制本文算法流程图，如图6所示。

图6 算法流程图Fig.6 Flow chart of the algorithm

4 仿真分析

通过仿真分析评估本文所提算法的成像性能，仿真参数如表1所示。以场景中心为坐标原点建立直角坐标系，选取的45个仿真点目标沿轴和轴均匀排列。每个点目标之间沿轴方向相距100 m，沿轴方向相距200 m，均匀地分布在成像区域内，如图7所示。图7中：为中心点，、为边缘点。

图7 点目标空间分布图Fig.7 Spatial distribution of target points

采用本文两步聚焦方法对45点目标阵成像所得到的高线图如图8所示，可见中心点和边缘点、都能很好聚焦，表明本文算法较好地解决了双基曲线SAR的二维空变问题，极大地提高了边缘点的聚焦性能。

图8 本文算法对45点目标阵成像的高线图Fig.8 Height plot of the 45-point target array imaged by the proposed algorithm

为进一步说明本文算法的优越性，对成像场景中的中心点和边缘点以及，进行单独放大显示，并将本文算法分别与文献[10]的RD算法、文献[11]的改进的RD算法以及文献[18]的EANLCS算法进行对比，结果如表2所示。

表2 不同算法的三点等高线图Tab.2 Three-point contour plotby applying different algorithms

观察表2可以发现，第1步粗聚焦后的三点仿真图，由于剩余空变相位的影响，严重影响成像质量，有必要进行第2步精确聚焦处理。经过第2步精确聚焦处理后，与另外3种算法相比，本文算法的等高线图无论是中心点还是边缘点、，其成像效果都更好，其他3种算法在边缘点都呈现了不同程度的散焦现象，说明其他3种算法在边缘点成像效果较差，成像场景有限。图9展示了不同算法的3个点的方位脉冲剖面图。

图9 不同算法的点目标方位脉冲剖面图比较Fig.9 Point-target azimuth pulse profiles by applying different algorithms

图9中，因为传统的RD算法未考虑SAR信号的二维空变问题，所以在边缘点和的方位剖面图出现了严重的散焦情况；而改进的RD算法因为引入了关于空变的剩余距离徙动矫正处理，其成像效果略好于传统的RD算法，但是该算法只补偿了距离向的1阶空变误差，所以边缘点仍然存在较为严重的散焦现象；文献[18]所提出的EANLCS算法，将多普勒参数关于目标的方位位置作泰勒展开，推导出各阶多普勒空变系数，然后引入EANLCS算法，较好地解决了方位相位有关于的空变性，但是忽略了变化带来的空变问题，因此相比于另外两种算法，其成像效果较好，但是还是出现了不同程度的散焦问题。由此可见，相比于上述3种方法，本文两步聚焦算法因为在距离向引入Keystone变换，方位向通过最小二乘拟合引入方位重采样方法，很好地补偿了距离向和方位向关于目标位置的二维空变相位误差，边缘点的聚焦性能得到了极大地改善。

此外，为了准确地比较4种算法的具体性能，表3列出了4种算法下的3个点目标性能参数。从表3可知，本文算法相对另外3种算法成像性能参数更好且分辨率更高，边缘点没有出现散焦的情况，且峰值旁瓣比(PSLR)和积分旁瓣比(ISLR)值都接近或者优于理论值-132 dB和-98 dB，表现出良好的聚焦性能。

表3 点目标的性能分析Tab.3 Performance analysis of point targets

通过上述高线图、方位脉冲响应以及点目标性能分析比较可知，本文提出的两步聚焦算法具有更好的成像精度以及更广的成像区域。

5 结论

本文基于双基曲线SAR的几何模型建立了空变分离的斜距等效模型，提出了一种适合双基曲线SAR的两步聚焦处理算法。第1步通过非空变相位补偿，完成粗聚焦。第2步对剩余的空变相位进行补偿：在距离向通过Keystone变换来去除距离向的主要空变相位；在方位向通过对多普勒参数的最小二乘拟合和方位重采样，来补偿各阶方位相位的空变误差，从而实现精确聚焦。得出主要结论如下：

1)本文提出的基于空变分离的斜距等效模型具有较高的精确性，满足成像要求。

2)本文提出的两步聚焦处理算法，有效解决了双基曲线SAR的二维空变难题。通过与其他算法作对比，验证了本文算法其成像性能更好，拥有更高的分辨率，适用于大场景模式。