基于深度自动编码器神经网络的飞行器翼型参数降维与优化设计
吴则良,叶建川,王江,金忍
(北京理工大学 宇航学院,北京 100081)
0 引言
随着计算流体力学的发展,气动外形优化在飞行器的设计中变得越来越重要,其中气动外形的参数化设计对气动外形优化起到至关重要的作用。良好的气动外形参数化设计方法需要满足在设计区间内以更少的设计参数覆盖更大的变形范围(尺度),以满足优化和创新设计的要求。
传统的翼型和机翼形状表征大多基于高维度的描述参数,如形函数线性扰动法、正交基函数法、自由变形法、特征参数描述(PARSEC)法和类别形状函数变换(CST)法等。在气动外形优化中,越大的设计空间和越多的参数变量能够覆盖越大的优化目标变化范围。但设计空间尺度和参数变量维度的增加会导致设计空间急剧膨胀,增加计算流体力学消耗的时间成本,同时增大遗传算法等智能全局搜索的优化算法寻找最优解的难度。目前部分学者采用代理模型的方法来解决这类高维度高计算成本的优化问题。Iuliano通过对比直接优化和代理模型优化,发现使用代理模型优化可有效减少计算流体动力学(CFD)的计算次数。但在代理模型的建立过程中,设计变量越多,建立具有合理精度的代理模型所需要的样本点就越多,所需样本数量也会随之呈指数倍增加,出现“维度灾难”的问题。
为解决该类问题,目前一部分学者采用改进的代理模型。Han等提出了变保真度的分层Kriging代理模型,对RAE2822翼型和三维运输机外形进行气动优化。另一部分学者提出了对设计变量进行降维的再优化求解。Wu等采用基于本征正交分解(POD)的方法对CST翼型描述方法进行降维处理,并证明了POD方法降维前后的翼型参数化方法在描述目标变化尺度具有同等的效果。
本文采用深度自动编码(DAE)算法对翼型描述参数进行降维,结果显示相对于POD算法,DAE算法能够适用更少的参数达到同样的参数降维效果。随后,采用基于DAE算法和Kriging代理模型的优化设计方法对RAE2822翼型进行跨声速来流下的减阻设计。结果显示,DAE算法相对于POD算法具有更优的参数降维能力,并可显著提升基于代理模型的翼型优化设计效率。
1 翼型参数降维设计
1.1 翼型库建立
在进行翼型的几何参数降维之前,需要先对翼型进行参数化描述并建立翼型数据库,常用的翼型参数化方法有PARSEC方法、Hick-Henne方法、正交基函数法、CST方法等。廖炎平等对几种翼型参数化方法拟合精度进行了对比研究,结果表明CST方法拟合精度较高,能产生连续光滑的几何外形。因此本文在翼型参数化过程选用CST方法。
CST方法是Kulfan提出的通过拟合翼型上下表面坐标点来描述翼型的一种方法,由于其良好的鲁棒性与精度,广泛运用于各类翼型参数化研究中。CST方法对翼型上下表面坐标点的描述规则如下:
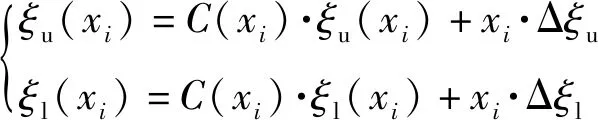
(1)
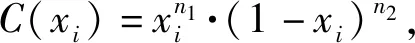
通常在使用CST方法对翼型进行拟合时,CST参数维数设置越高,对翼型拟合效果越好,但过高维度的参数也将增加计算成本。本文采用18维的CST方法对RAE2822翼型进行描述,以拟合前后翼型上下表面坐标点的残差衡量翼型的拟合精度。经CST方法拟合对RAE2822翼型的拟合效果以及残差如图1和图2所示,可见其上下表面拟合前后坐标点的残差均控制在10以内,认为CST方法满足翼型参数化要求。
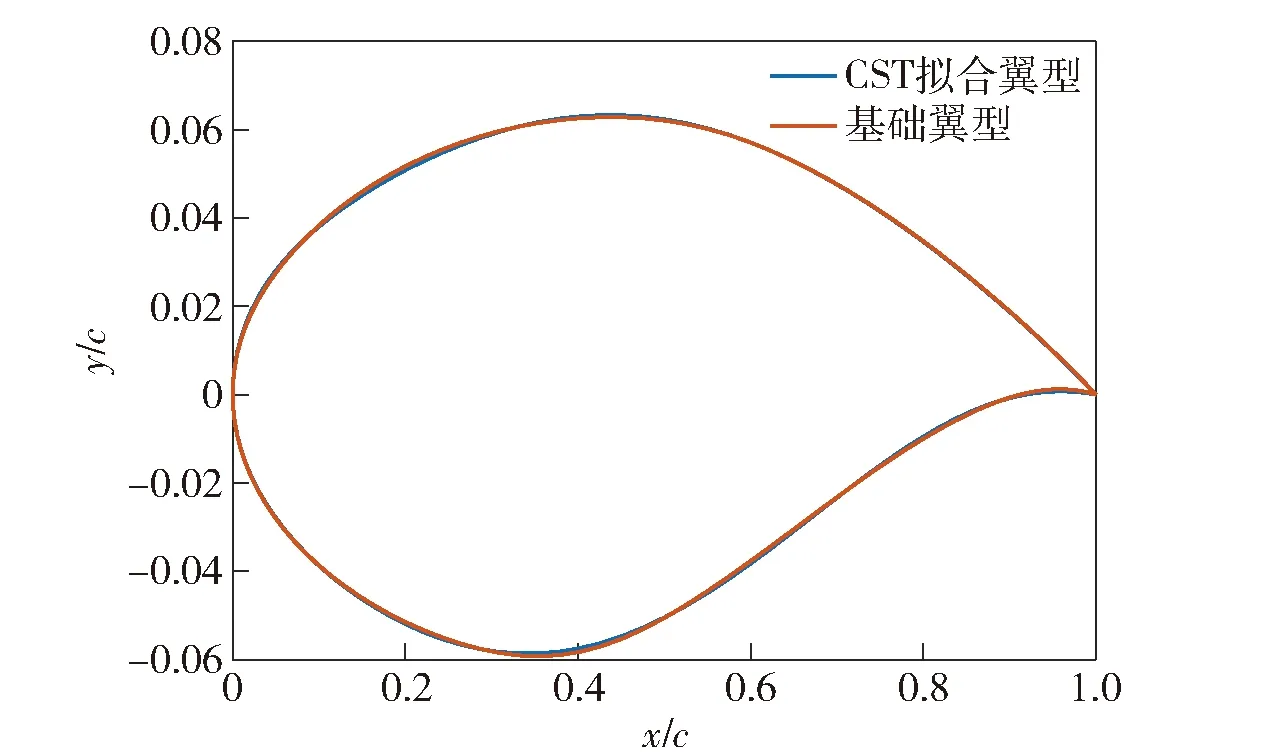
图1 基于CST方法的RAE2822翼型拟合结果Fig.1 RAE2822 airfoil fitting resultsobtained by CST method
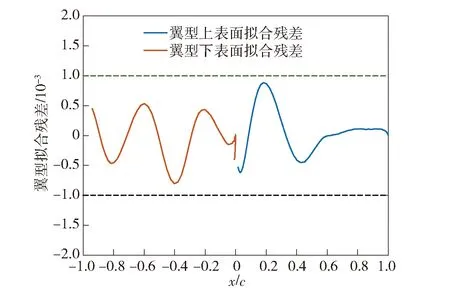
图2 基于CST方法的RAE2822翼型拟合残差(横坐标-1~0代表翼型下表面,0~1代表翼型上表面)Fig.2 Fitting residual of RAE2822 airfoil obtained by CST method(-1-0:the lower surface;0-1:the upper surface)
为保证翼型优化过程中生成新翼型的合理性,需要对每种翼型参数化方法设计变量设置一定的上下界,工程上一般认为±10%~±20%可以满足要求。为提高翼型优化效果,本文在RAE2822翼型的拟合基础上选择设计变量的上下边界(±20%)作为设计空间,并基于拉丁超次方抽样方法生成用于参数降维训练的翼型数据库。拉丁超次方抽样方法是一种分层随机抽样,能够确保对每个变量范围的全覆盖。生成的翼型设计空间如图3所示。
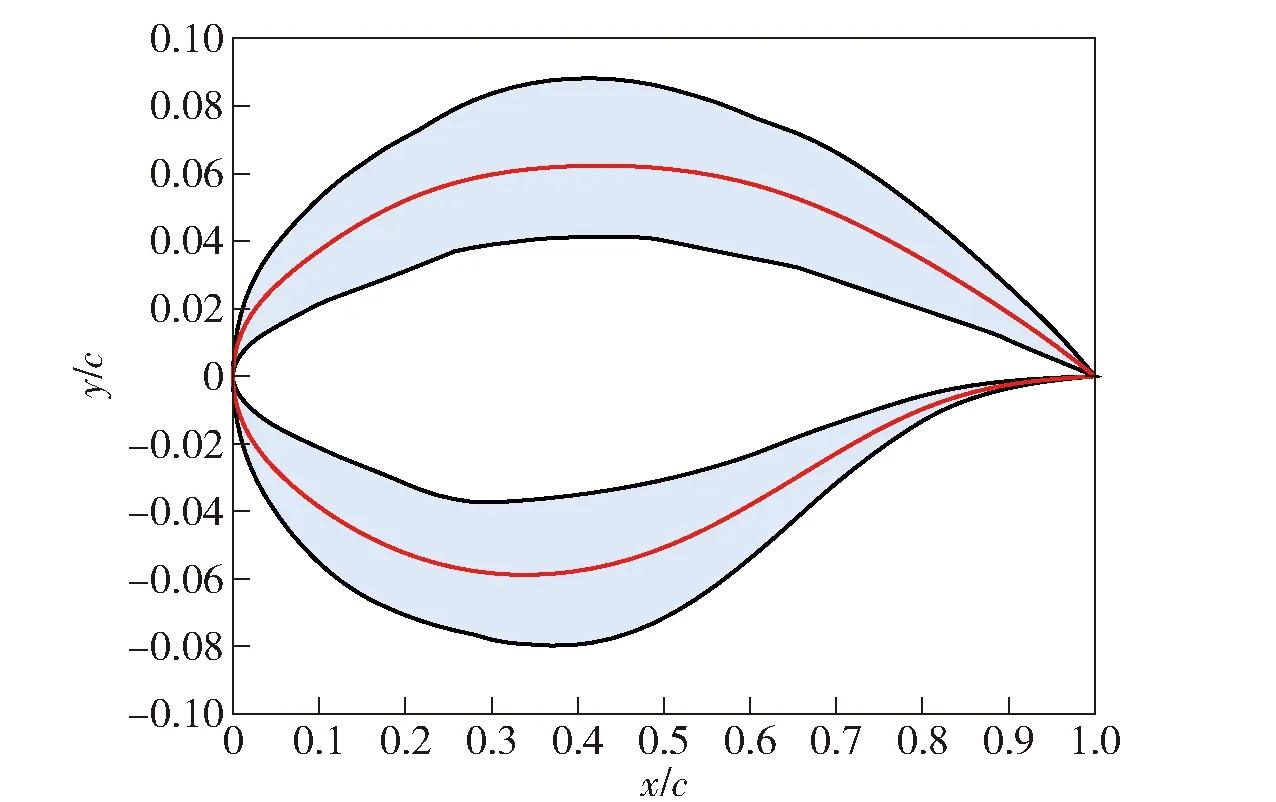
图3 基于CST方法的翼型设计空间Fig.3 Airfoil design space based on CST method
数据库中的翼型可以用个二维坐标点统一表示,其中每个翼型的坐标保持一致,因此翼型数据库可以用其中各翼型的坐标(()=[,,…,])来表示,此处是一个×阶矩阵,其中为数据库中的翼型个数,代表每一个翼型特征点的个数。本文采用RAE2822翼型为基础翼型,其二维坐标采用NASA翼型数据库数据,有=130。
1.2 参数降维方法
1.2.1 本征正交分解法
POD法是一种用于获得高维数据的低维近似的数据分析方法,在1933年首次由Hotelling正式提出,现已广泛应用于各学科领域。POD通过降低数据重要性,可以实现将数据库中的数据分解为一组正交基函数。假设有个不相关的数据,每个数据都可以用一个维特征向量()()表示,则这组数据可定义×阶矩阵(×)。POD的原理是用维数更少的矩阵′(′×′)来表示描述的线性空间,即′≤。Chatterjee对POD降维算法进行了详细推导和分析,其可转化为如下约束极值问题:
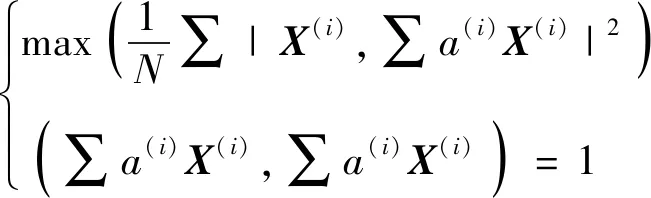
(2)
式中:|·,·|和(·,·)分别为内积运算和内积运算的范数运算;()为基向量构成的矩阵的元素,=[,,…,()]。(2)式也可以通过在核函数和基向量之间定义核函数和算子来表征,即
=λ
(3)
式中:(×)为的协方差矩阵;为矩阵的特征根。
中的每个元素可通过(4)式计算得到:
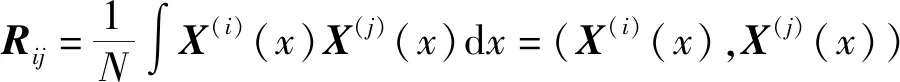
(4)
显然,是一个对称的非负矩阵,并具有一组特征根()和特征向量()。依据特征根()将特征向量()排列,可求得系数矩阵。
降维后的矩阵′可通过(5)式求得:
′=·
(5)
式中:为系数矩阵的前′列。
1.2.2 基于DAE的神经网络模型法
自动编码器的概念最早由Rumelhart等在1986年提出,它最初作为一种数据压缩算法被用作处理高维复杂数据,具有如下特性:
1)数据相关特性,DAE可以用来压缩与编码特征分布相似于训练样本的数据,应用到翼型描述参数的降维是合理的;
2)自编码器的数据压缩是有损的,在本文中用于简化翼型数据的描述,可实现快速概念设计。
3)自动编码器能够从训练数据中自动学习特征压缩与编码,减轻概念设计阶段的计算工作,且该方法具有一定通用价值,不依赖于特定翼型结构。
DAE主要由两部分组成,一是编码器=(),用于将输入数据压缩成一个维数较小的码向量,也称为隐层;二是解码器,用于生成重构函数=(),用来将编码的矢量还原为原始的输入数据。在训练过程中,需要为DAE设置损失函数,测量解码器恢复数据的程度或由于特征压缩造成的信息丢失。编码和解码网络中的参数可通过采用随机梯度下降等算法,通过最小化损失函数来求得。
近年来,随着计算机性能的提升,深度神经网络的训练成为可能。2012年,Krizhevsky等使用先进的非线性单位、正则化技术取得了优秀的训练效果。2015年,Ioffe等提出的批标准化技术可以有效地训练更深层的神经网络。2016年,Cheng等提出了残差网络,使任何深度的网络都能进行有效训练。
与自动编码器相比,DAE增加了深度,提高了学习能力,更有利于预训练。如图4所示,对于一个由5层结构构成的DAE,隐层的节点数量先降低再升高,最终只需要得到矢量[]和解码层的参数就可以输出最终的重构数据,其中为DAE网络结构隐层中的参数。
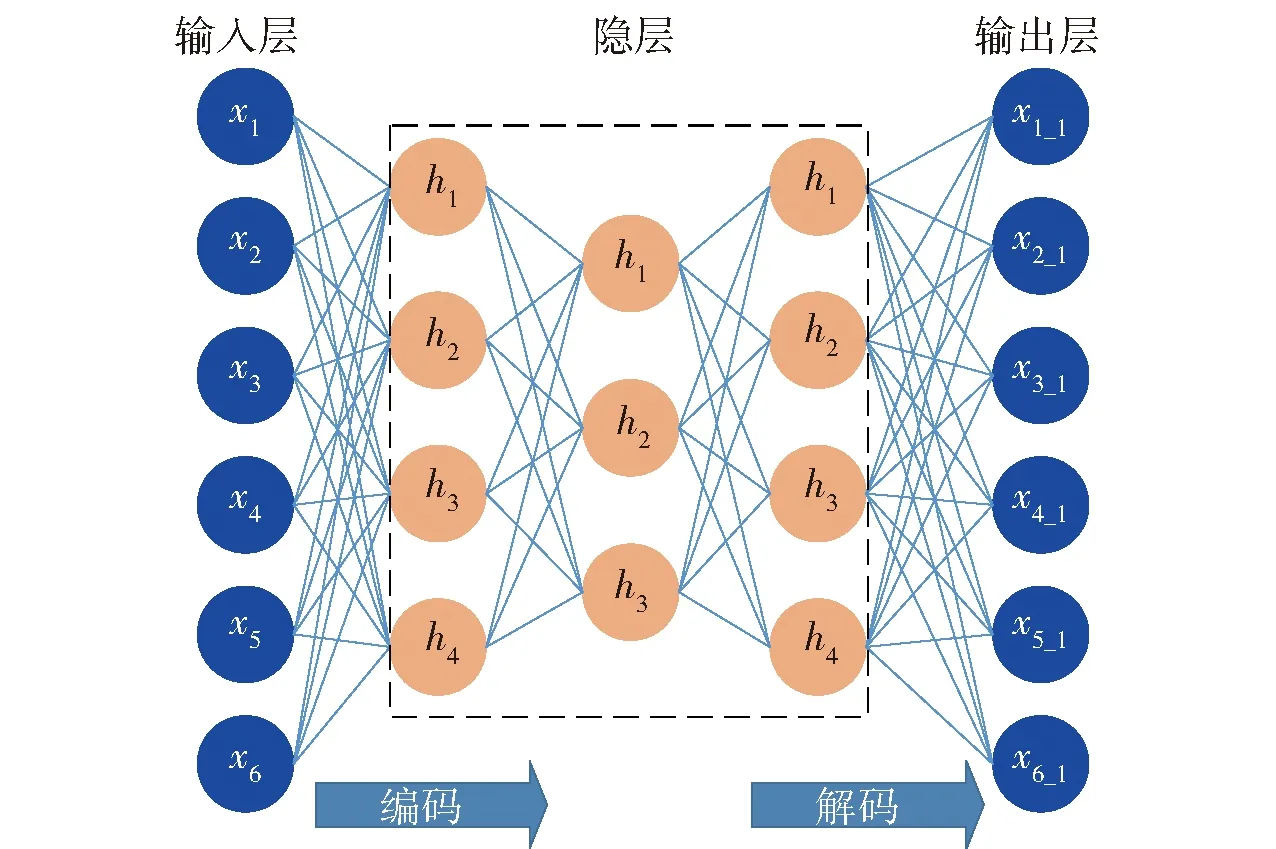
图4 DAE网络结构Fig.4 DAE network structure
1.3 翼型参数降维
1.3.1 基于POD的翼型参数降维
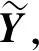
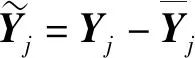
(6)
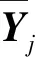
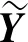
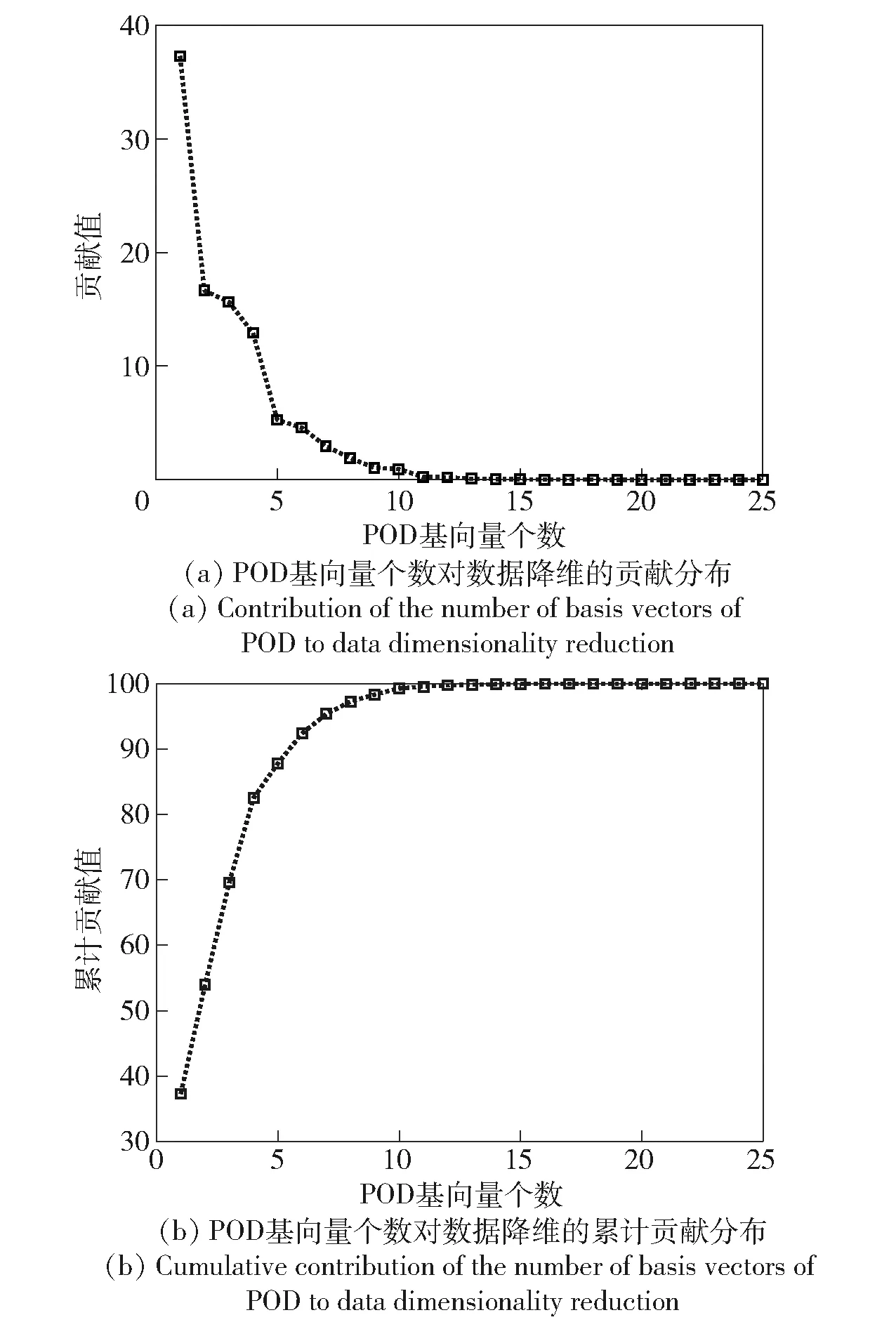
图5 POD基向量对于数据降维的贡献值和累计贡献值Fig.5 Contribution and cumulative contribution of basis vectors of POD to data dimensionality reduction
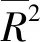
在翼型库中随机抽取4个翼型,其经POD-7降维前后翼型形状对比和拟合误差如图6和图7所示,可以看出经POD-7降维后的翼型坐标点纵坐标误差基本在±0.005以内,满足翼型参数拟合要求。
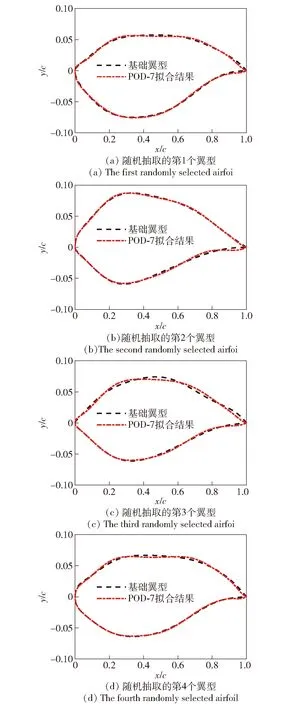
图6 POD-7降维前后翼型对比Fig.6 Comparison of airfoils before and after POD-7
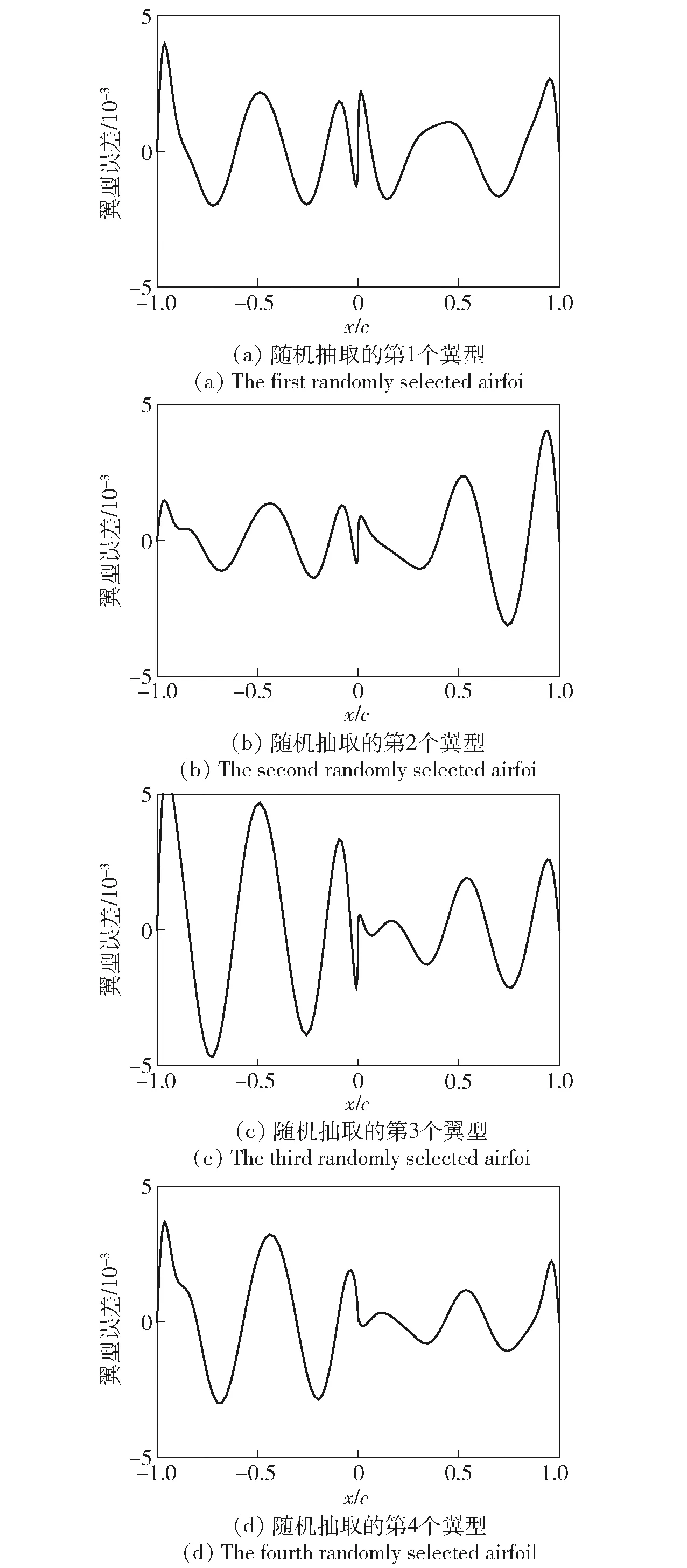
图7 POD-7降维前后翼型误差曲线Fig.7 Error curves of airfoils before and after POD-7
均方差′定义如下:
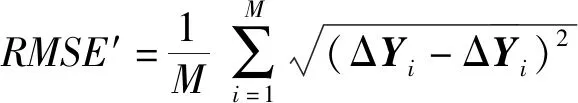
(7)
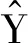
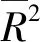
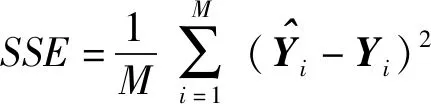
(8)
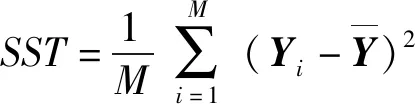
(9)
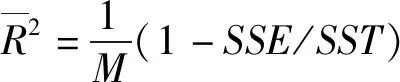
(10)
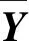
132 基于DAE的翼型参数降维
DAE模型将翼型数据库作为输入,如图8所示(图中表示隐层结构),DAE神经网络包括输入层、输出层、隐层、编码降维层、解码重构层。编码降维层设置4层,隐层节点数为编码降维最后一层节点数的一半。解码重构各层节点数与编码降维层相对称。
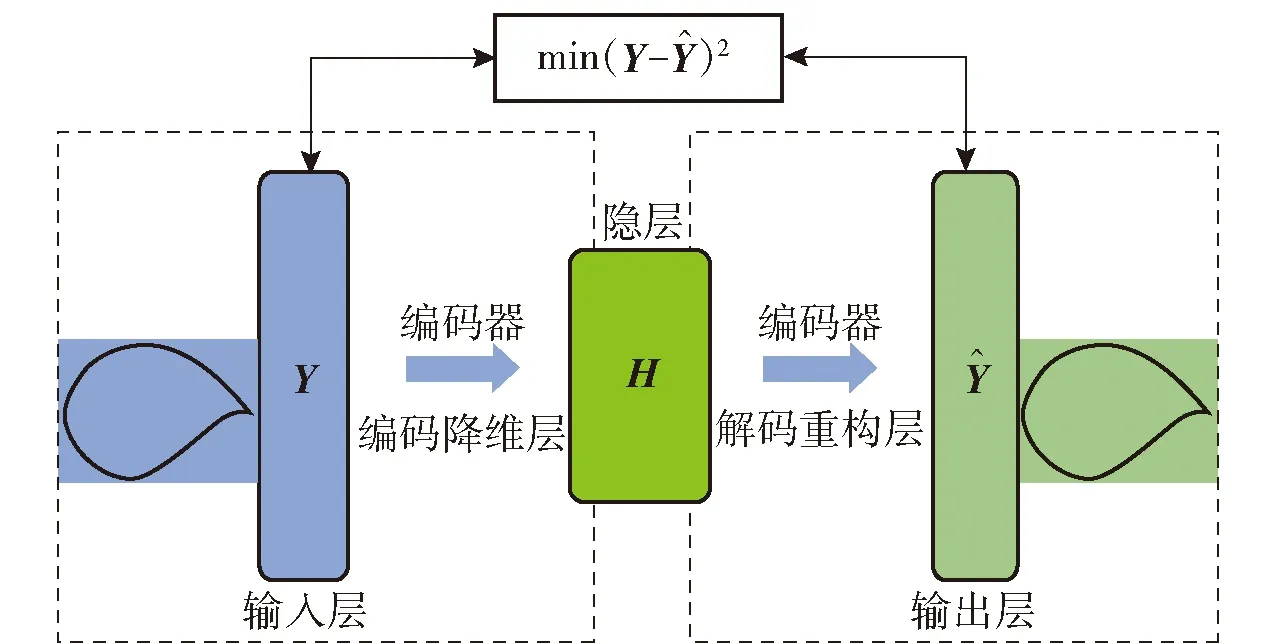
图8 DAE神经网络参数降维框架Fig.8 Parameter dimensionality reduction framework of DAE neural network
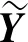
=1-
(11)
由(11)式可以看出,越接近于0,翼型降维前后的损失越小。本文分别对DAE神经网络隐层节点数为6(DAE-6)和节点数为7(DAE-7)的模型进行无监督训练,DAE-6训练过程的随迭代步数变化如图9所示。
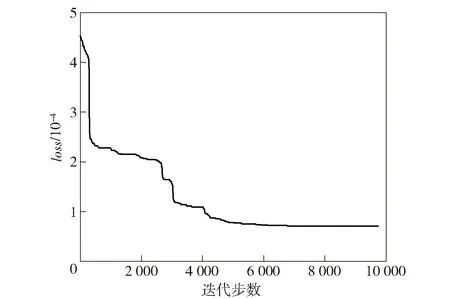
图9 loss随迭代步数变化曲线Fig.9 loss versus iterative step
经DAE-6模型进行训练前后翼型对比如图10和图11所示,可以看出降维前后翼型的拟合误差均严格控制在±0005以内,对比图7可以看出,经DAE-6降维后的翼型拟合误差要显著小于POD-7。
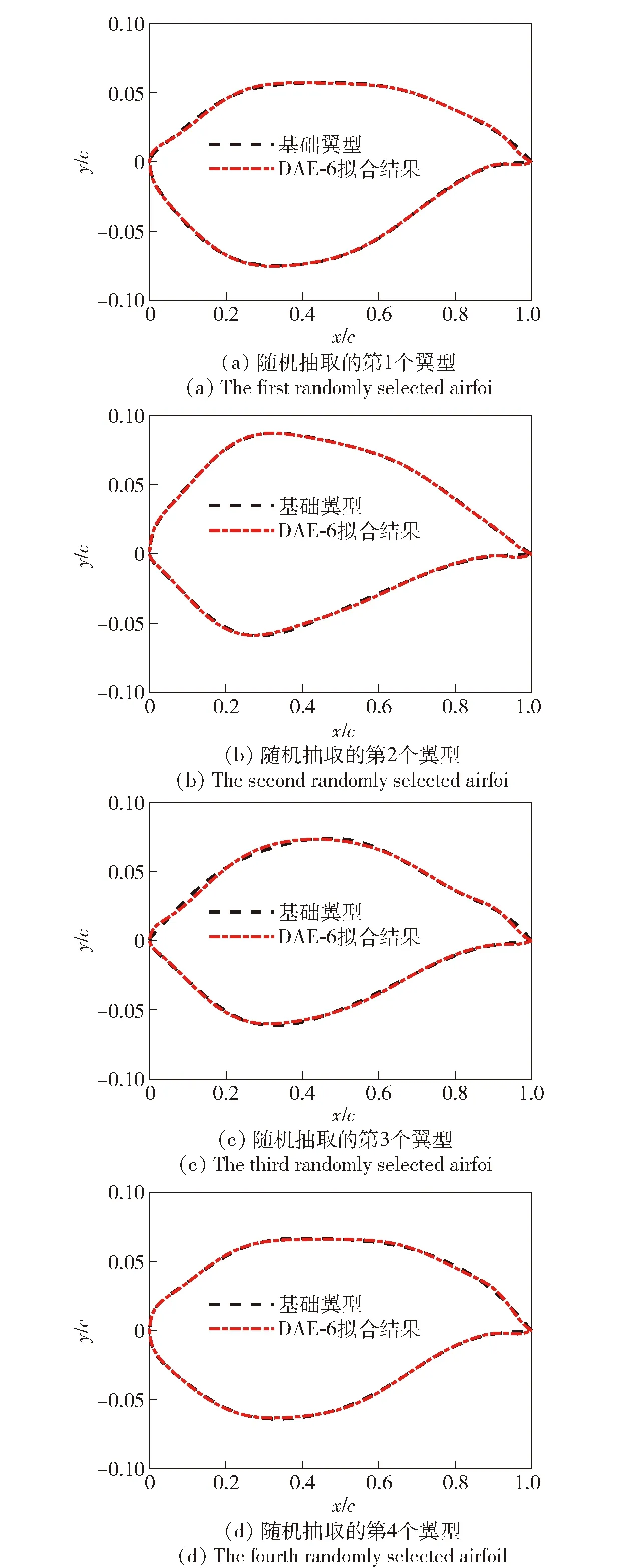
图10 DAE-6降维前后翼型对比Fig.10 Comparision of airfoils before and after POD-6
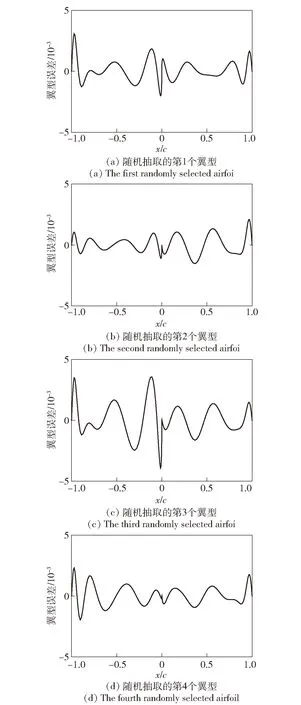
图11 DAE-6降维前后翼型误差曲线Fig.11 Error curves of airfoils before and after DAE-6
DAE-6隐层中的翼型设计参数可以表示为
=[,,,,,]
(12)
通过分别改变每个参数,可以分析(12)式中每个变量对翼型几何特性的影响如图12所示。由图12可以看出DAE-6中每个参数均对翼型的几何特性产生全局影响:的变化主要影响翼型上表面最大厚度位置和下表面最大厚度位置;的变化主要影响翼型上表面最大厚度位置;的变化主要影响翼型下表面尾缘的形状;的变化主要影响翼型上表面最大厚度以及下表面前缘半径;的变化主要影响翼型的最大厚度;的变化主要影响翼型下表面最大厚度以及上表面尾缘的形状。
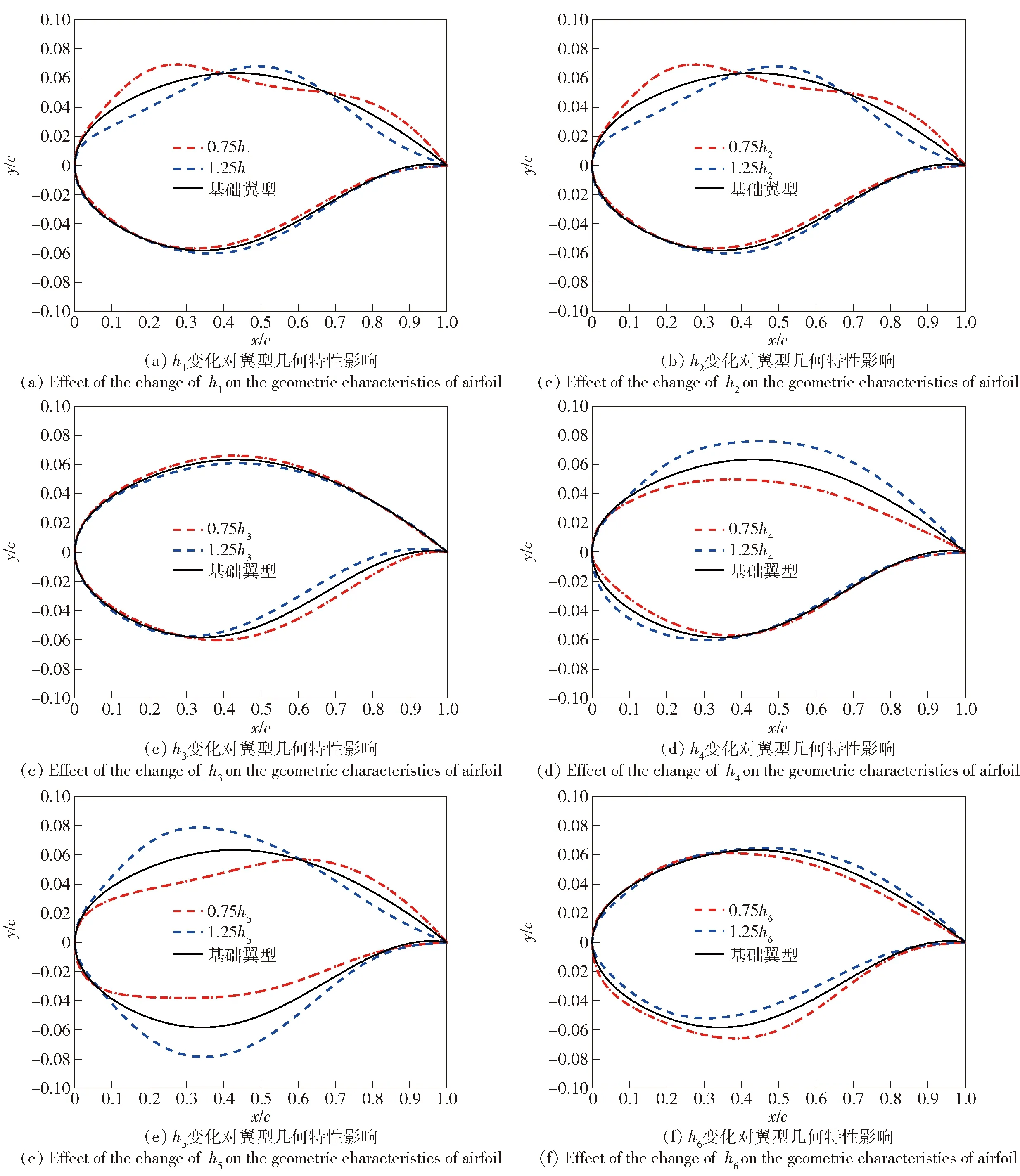
图12 DAE-6各参数对翼型描述的影响Fig.12 Effect of DAE-6 parameters on airfoil description
1.4 翼型参数降维效果对比
本文中所验证的翼型参数降维方法效果如表1所示。
从表1中可以看出,进行相同维度的翼型参数降维时,DAE效果要显著优于POD,DAE-6可达到与POD-7相同的翼型参数降维效果。因此本文选用DAE-6和POD-7对RAE2822翼型进行参数降维与优化设计。

表1 各方法翼型参数降维效果对比Tab.1 Effect comparison of dimensionality reduction of airfoil parameters
2 翼型优化设计
本文针对跨声速条件下RAE2822翼型进行减阻设计,流场相关参数设置为雷诺数=65×10,马赫数=0734,攻角=271°。优化设计目标与约束条件为
min
(13)
s.t.>
(14)
≤
(15)
≥
(16)
式中:为翼型阻力系数;为翼型升力系数;为翼型的俯仰力矩系数;为翼型几何面积;、、分别为RAE2822翼型的升力系数、阻力系数和翼型横截面积,具体参数取值如表2所示。

表2 RAE2822翼型相关气动参数Tab.2 Aerodynamic parameters of RAE2822 airfoil
本文翼型优化设计流程如图13所示。在翼型优化设计过程中,本文使用18维参数的CST方法取新的补充样本点;在优化过程中选用遗传算法进行设计空间内的寻优。
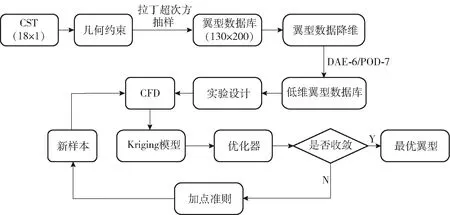
图13 翼型优化设计流程图Fig.13 Airfoil optimization design framework
(CST18)作为优化设计的参考基准;在获取初始翼型数据库时,本文采用拉丁超次方抽样,以保证对设计的几何约束范围实现全覆盖,初始翼型数据库中包含200个样本;选用Kriging模型来构建替代模型,用于减少仿真次数,提高优化设计流程效率;利用目标函数最小化准则和最大期望提高准则获
值得指出的是,本文对翼型数据进行降维过程中,不论选择POD-7方法还是DAE-6方法,均会产生一定的仿真和训练时间成本,但对比构建Kriging模型和经遗传算法对翼型寻优,并利用CFD进行气动性能仿真计算所需的时间成本,翼型数据降维环节的时间成本影响可以忽略不计,因此可以认为POD-7方法和DAE-6方法对本文翼型优化设计与计算效率的影响无显著差异。
翼型优化设计结果如图14~图16所示。其中图14为经CFD仿真的各参数化方法下翼型优化结果的阻力系数分布曲线。由图14可以看出,经优化设计后的翼型在跨声速条件下激波明显减弱,其中经DAE-6优化设计的翼型在跨声速流场下的CFD仿真压强云图和速度云图如图17和图18(为来流速度)所示。由图15可以看出,各参数化方法下的翼型优化结果均与原RAE2822翼型几何形状有显著差异,主要体现在翼型上下表面最大高度位置以及上下表面最大曲率。观察图16可知,相对于CST18,POD-7和DAE-6能够显著提升优化收敛速度,并且DAE-6的优化收敛速度快于POD-7,证明DAE-6在翼型优化效率与描述潜在翼型方面的能力要更优于POD-7。
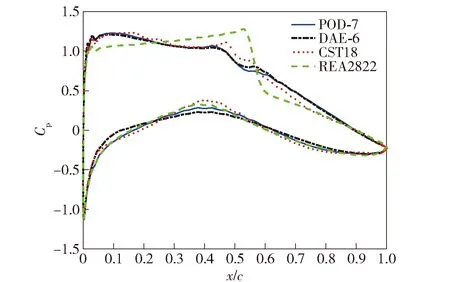
图14 各参数化方法下翼型优化结果Cp分布Fig.14 Cp of airfoil optimized results of each parameterization method
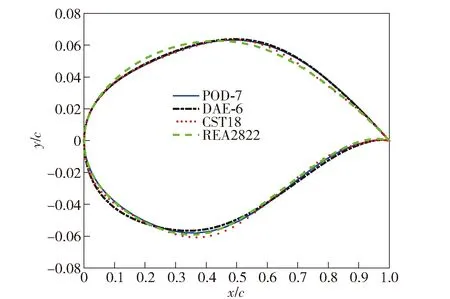
图15 各参数化方法下翼型优化结果几何形状对比Fig.15 Comparison of airfoil optimized results under each parameterization methods
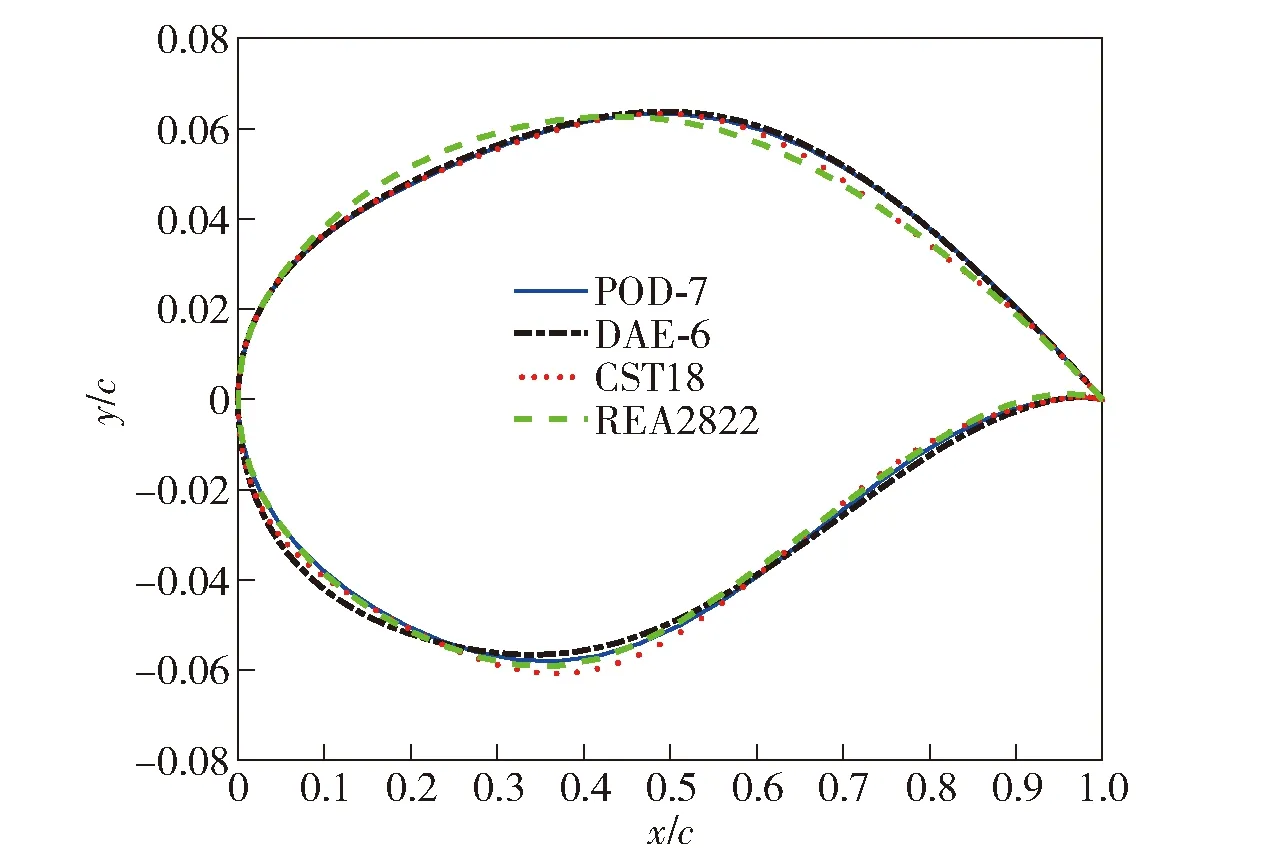
图16 各参数化方法下翼型优化过程Cp收敛情况Fig.16 Convergence of Cp in airfoil optimization process of each parameterization methods
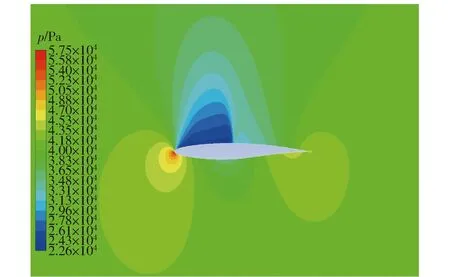
图17 经DAE-6优化后的翼型CFD仿真压强云图Fig.17 CFD pressure contour of airfoil optimized by DAE-6
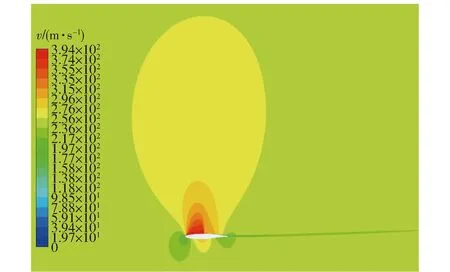
图18 经DAE-6优化后的翼型CFD仿真的速度云图Fig.8 CFD velocity contour of airfoil optimized by DAE-6
在预设计算条件下,经Fluent软件对RAE2822翼型进行跨声速流动下的气动性能仿真计算,得出该条件下RAE2822的为0.018 5。由图16可以看出,CST-18、POD-7和DAE-6均能满足跨声速流动下对RAE2822翼型的优化设计目标,对比三者优化设计结果,经DAE-6降维优化的翼型阻力系数比经CST-18拟合优化的降低11.61%,经POD-7降维优化的翼型阻力系数比经CST-18拟合优化的降低9.74%,证明DAE-6在该设计目标下对RAE2822翼型的减阻优化设计效果优于POD-7。
3 结论
本文介绍了POD和DAE两种数据降维算法在二维翼型参数降维中的应用,并验证了二者均可以在允许的误差范围内大幅度减少翼型描述参数的个数。本文将POD与DAE两种方法分别与代理模型相结合,对RAE2822翼型进行跨声速条件下的优化设计。得出主要结论如下:
1)POD和DAE可以在使用少量变量参数条件下大幅度提升翼型优化效率,并减小遗传算法寻优压力以及减少代理模型初始样本个数。
2)通过对比CST-18、POD-7、DAE-6对RAE2822翼型优化优化设计结果,证明DAE-6方法在提高优化设计效率、降低翼型阻力系数方面效果更优。

