复合材料层合板鸟弹撞击损伤分析

王 浪，孙有朝，周亚东，杨 坤，曾海军，陈 川

（1.南京航空航天大学民航学院，南京 210016；2.中国航发商用航空发动机有限责任公司，上海 200241；3.中国南方航空公司股份有限公司，广州 510470）

0 引言

随着中国经济和科技的快速发展，飞机的数量和班次都在不断增加，因鸟撞而发生的飞机安全事故也越来越多，据统计，在飞机的地面安全事故中，鸟类碰撞事故占21%。其中大量事故的起因是鸟类被吸入航空发动机，造成发动机叶片变形，进而导致发动机推力降低、叶片断裂等严重后果，严重威胁民用和军用航空的安全，引起国际社会的高度重视。因此，设计和研究航空发动机叶片防鸟撞击保护装置对于提高航空飞行的安全性、减少财产损失、保障乘客生命安全具有极其重要的意义。

为避免鸟撞飞机事件的发生，提高航空器结构的抗鸟撞击能力，迫切需要通过开发高性能材料和更好的耐撞性设计来提高飞机风扇叶片结构的抗鸟撞性能。一般来说，鸟撞是持续时间短（一般在毫秒范围内)的高强度载荷加载事件，具有复杂的耦合相互作用。在鸟弹的软体撞击作用下，鸟弹的几何效应、材料模型，以及初始速度和落角等关键参数都会影响风扇叶片结构的变形和损伤机理。为了解决复合材料风扇叶片在鸟弹高速冲击下变形和损坏的问题，Hedayati等研究了平板不同厚度、铺层方式对平板鸟撞总能量的影响；Di等研究了鸟撞风扇叶片层合板厚度对飞机的影响，计算出鸟撞层合板的临界厚度；Zhou等在不改变整体几何形状的情况下，考虑了不同材料体系（不同铺层顺序和总厚度)的鸟击耐撞性；Kim等、Siddens等分别采用任意拉格朗日-欧拉（Arbitrary Lagrange-Euler，ALE)方法和无网格拉格朗日粒子方法研究了被鸟击中的单个风扇叶片的初始退化，并评估了对其他发动机部件的后续损坏；Heimbs等介绍了在软体冲击下承受拉伸和压缩预载荷的层压复合板的动态行为，发现拉伸和压缩预加载会对损坏模式产生影响。上述研究表明，影响叠层复合材料鸟撞损伤的关键因素包括层合板的总厚度、铺层角度、转速和撞击位置等。

本文进行了鸟弹在4个角度下撞击复合材料层合板的试验，并进行了数值模拟，建立了复合材料层合板靶板，分析了复合材料层合板与弹体发生碰撞后的受力情况，建立风扇真实模型模拟鸟弹撞击风扇。

1 复合材料层合板鸟撞数值模拟

1.1 鸟弹几何模型的建立及网格划分

利用Ironpython语言对弹体尺寸以及复合材料层合板靶板尺寸进行参数化，定义鸟弹以及复合材料层合板的尺寸与实际试验状态下的尺寸一致，程序化方法有利于模型生成，同时缩短工作时间。将鸟弹形状简化为圆柱体，鸟弹几何尺寸如图1所示，靶板为长方形。对鸟弹模型进行全六面体网格划分，网格数量为9483，鸟弹模型网格划分如图2所示。

1.2 复合材料层合板几何模型的建立

对复合材料层合板壳体进行建模，将网格模型生成K文件导入Isprepost进行TSHELL单元的铺层，为便于定义每层材料，分别对每层的积分点进行层数定义。从板上方到板下方共分5层，每层的铺层角度分别为0°、45°、90°、-45°、0°，网格数量为3960。复合材料层合板尺寸、模型网格如图3、4所示。

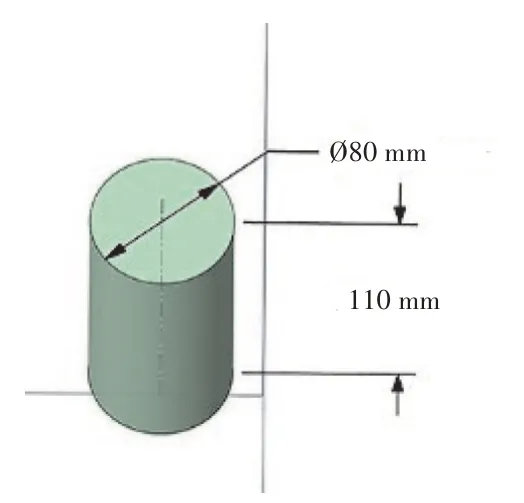
图1 鸟弹几何尺寸

图2 鸟弹模型网格

图3 复合材料层合板尺寸

图4 复合材料层合板模型网格

图5 在不同入射角度下鸟弹撞击的组装弹体-靶板模型

鸟弹在不同入射角度下撞击靶板时的组装弹体-靶板模型如图5所示。图中红色矩形为鸟弹，绿色矩形为靶板，鸟弹入射角度为靶板与重力方向夹角，分别为0°、15°、30°、45°，鸟弹撞击在矩形靶板一条长边的中部。

考虑到边界效应的影响，试验采用全模型进行仿真计算。

1.3 仿真计算约束和材料模型的确立

1.3.1 仿真计算约束条件的设置

该仿真计算模型采用ANSYS/LSDYNA中的拉格朗日算法，弹体与复合材料层合板之间的接触为侵蚀接 触（*CONTACT_ERODING_SURFACE_TO_SURFACE，简称为ESTS），建立的全模型无需设置对称边界约束，同时根据试验条件，在目标板件单短边施加固定边界约束，弹体速度设置为140 m/s。具体约束条件如图6所示，在试验中平板采用一端悬臂的方式夹持，如图7所示。

图6 目标板件的约束条件

图7 试验平板一端悬臂夹持

1.3.2 仿真计算材料模型的设置

数值模拟面临的挑战之一是建立一个合适的弹体和复合材料层合板材料模型，本文考虑到试验中鸟弹出现的流体分散现象，采用*MAT_ELASTIC_PLASTIC_HYDRO材料模型。

靶板模拟采用LS-DYNA中的COMPOSITE损伤材料模型，该模型适合描述复合材料等脆性材料在大应变、高应变率和高压下的动态响应，鸟弹和靶板材料模型参数分别见表1、2，其中靶板、方向分别为靶板长边、短边方向，方向为与靶板垂直的方向。

表1 鸟弹材料模型参数

表2 靶板材料模型参数

2 数值模拟结果分析

在上述模型的基础上，对数值模拟鸟撞复合材料层合板损伤情况进行了分析。在0°、15°、30°、45°4个角度下鸟弹与复合材料层合板接触的运动过程如图8所示。由于复合材料层合板角度发生变化，初始撞击时间不相同。在4个角度下鸟弹的速度时程曲线如图9所示。从图中可见，在4个角度下复合材料层合板的鸟弹初始速度均为140 m/s，当复合材料层合板与鸟弹接触时，鸟弹的速度开始减小，45°复合材料层合板最先与鸟弹接触，其次分别是30°、15°、0°复合材料层合板，而后随着时间的延长，鸟弹速度不断减小。45°复合材料层合板的鸟弹速度达到平衡的时间最短，但30°复合材料层合板的残余速度最小。

图8 在不同入射角度下鸟弹弹体与复合材料层合板接触的运动过程

图9 在不同入射角度下鸟弹的速度时程曲线

鸟弹沿风扇进气方向撞击风扇叶片时，切鸟角度会改变，不同角度的撞击对叶片造成的损伤也不同。为了分析复合材料层合板与鸟弹碰撞后的受力情况，对4个角度下复合材料层合板与弹体碰撞进行了数值模拟，不同角度下复合材料层合板的应力如图10所示。从图10（a）中可见，0°复合材料层合板在第1.11 ms时产生应力，在第1.19 ms时开始出现裂纹，裂纹从断裂位置呈折线形延展，在第1.77 ms时复合材料层合板全部断裂；从图10（b）中可见，15°复合材料层合板在第0.93 ms时产生应力，在第1.04 ms时出现裂纹，裂纹从断裂位置呈折线形延展，在第1.63 ms时复合材料层合板全部断裂；从图10（c）中可见，30°复合材料层合板在第0.76 ms时产生应力，在第0.91 ms时开始出现裂纹，与0°和15°复合材料层合板不同，裂纹呈直线形延展，在第1.61 ms时层合板完全断裂；从图10（d）中可见，45°复合材料层合板在第0.61 ms时产生应力，在第0.82 ms时出现裂纹，与30°复合材料层合板破坏裂缝相同，裂纹呈直线形延展，在第1.57 ms时平板完全断裂。可见由于角度不同，鸟弹距复合材料层合板的距离也不同，角度越大，距离越近，鸟弹与复合材料层合板接触的时间越短，但观察到一个有趣的现象，角度越大，复合材料层合板从开始产生应力到出现裂纹的时间越长，说明角度越大，复合材料层合板的抗鸟撞效果越好。综合比较鸟弹的残余速度和复合材料层合板的损坏情况可知，鸟弹入射角度为30°时复合材料层合板的抗鸟撞效果最好。

图10 在不同入射角度下鸟弹撞击时复合材料层合板的应力分析

在4个不同入射角度下鸟弹撞击复合材料层合板时，复合材料层合板应变随时间变化的试验结果与数值模拟结果对比如图11所示。图中实线为仿真结果曲线，虚线为试验结果曲线；应变仿真结果最大值与试验结果最大值的比较见表3。仿真结果与试验结果的误差

从表3中可见，应变仿真结果与试验结果的误差在10%以内，验证了数值模型的正确性。

图11 在不同入射角下鸟弹撞击时复合材料层合板应变随时间变化的试验与数值模拟结果对比

表3 复合材料层合板应变最大值仿真结果与试验结果的比较

为模拟真实环境下鸟弹撞击风扇叶片的情况，建立风扇叶片的计算模型，如图12所示。

风扇转速为6000 r/min时，在不同入射角度（通过投鸟角度改变）下鸟弹撞击的速度时程曲线如图13所示。鸟弹初始速度均为140 m/s，不同入射角度下鸟弹与风扇叶片碰撞的时刻分别为：0°时为第0.79 ms，15°时为第0.62 ms，30°时为第0.47 ms，45°时为第0.79 ms。从图中可见，入射角度越大，鸟弹与风扇叶片的接触时间就越短，这与试验结果一致，且角度为30°时，复合材料层合板的残余速度最小，这在工程上十分有利。

图12 风扇叶片计算模型

图13 风扇转速为6000 r/min时，在不同入射角度下鸟弹撞击的速度时程曲线

在不同入射角度下鸟弹位移随时间变化曲线如图14所示。从图中可见，各角度下鸟弹撞击初始时刻的位移均为0，而后随着时间的延长，各角度下鸟弹位移不断增大，呈线性增长趋势，可以看到风扇叶片位移在0°时最大，在15°时次之，在30°和45°时几乎相等。

对鸟弹与风扇叶片靶板接触的单元进行应力分析，各角度下接触单元的应力最大值如图15所示。从图中可见，风扇叶片靶板的应力在鸟弹入射角度为0°时最小，随着入射角度的增大，风扇叶片靶板的应力也随之增大，在入射角度为15°和30°时应力值相差不多，在45°时应力最大。综上所述，在风扇叶片靶板为30°时，鸟弹残余速度最小，风扇叶片靶板的位移最小，承受应力较小，靶板的抗鸟撞效果也最好。

3 结论

图14 在不同入射角度下鸟弹撞击时风扇叶片位移随时间变化的曲线

图15 在不同入射角度下风扇叶片靶板接触单元的应力最大值

（1）复合材料层合板鸟撞数值模拟结果与试验结果一致，综合比较鸟弹的残余速度和复合材料层合板的损坏情况，发现在鸟弹入射角度为30°时复合材料层合板的抗鸟撞效果最好。

（2）风扇转速为6000 r/min时，鸟弹入射角度越大，鸟弹与风扇叶片接触的时间就越短，接触碰撞后鸟弹的速度减小越多、残余速度越小。鸟弹入射角度为30°时，复合材料层合板的抗鸟撞效果仍然最好。