基于改进AFSA的桨扇发动机加速控制计划优化
邢耀仁,黄向华
(南京航空航天大学能源与动力学院,南京 210016)
0 引言
航空发动机的过渡态是指发动机由一种工作状态改变到另一种工作状态的变化过程,加速时间是衡量发动机过渡态性能的重要指标之一。在满足发动机性能参数约束的前提下,尽可能缩短加速时间可以最大限度地提升发动机动态性能,因此对加速控制计划进行优化具有重要的工程应用价值。
航空发动机是气动热力计算高度复杂的非线性系统,直接对其进行满足参数约束下的过渡态性能寻优很困难,目前常用的寻优方法有2种:(1)功率提取法,即在发动机稳态模型基础上,从高、低压转子提取额外的功率,使高压压气机的起动工作点沿着等换算转速线移动,在满足约束前提下,尽可能使提取功率更大,从而获得最佳的加速控制规律;(2)动态规划法,即在发动机动态模型基础上建立可以实现性能需求的目标函数,并求解1个有约束的泛函优化问题,该方法目前被广泛应用于发动机过渡态控制优化中。运用的主要优化算法有约束变尺度法、序列二 次 规 划 法(Sequential Quadratic Programming,SQP)、线性二次型调节器(Linear Quadratic Regulator,LQR)法、自适应方法和元启发式算法等。由于约束变尺度法等传统算法都是基于梯度概念来寻优的,既要求目标函数和约束条件可微,又容易陷入局部最优解中。而启发式算法通过模仿自然选择过程,具有了生物进化的2个优势——强化和多样性。其中强化可以使算法向最优值附近搜索,多样性可以保证最优值的全局最优性。人工鱼群算法(Artificial Fish Swarm Algorithm,AFSA)是一种基于鱼群行为的启发式算法,具有简单的结构形式和较好的全局寻优能力,在各类优化问题中得到了广泛应用。王锡淮等通过引入半可行域的概念,提升了人工鱼群算法求解带约束问题的能力;范永利等针对人工鱼群算法难以综合考虑寻优速度和寻优精度的不足,通过引入双高斯函数对算法进行了改进,提高了算法的全局寻优能力和搜索速度。
本文引入自适应调整策略和半可行域对人工鱼群算法进行改进,在此基础上,提出了一种桨扇发动机加速控制计划的优化方法。
1 桨扇发动机过渡态控制问题
桨扇发动机作为一种介于传统涡桨发动机和涡扇发动机之间的新概念发动机,具有优于涡桨发动机的高速性能和高于涡扇发动机的燃油效率。随着环保要求的不断提高,航空业对高效率、低排放动力装置的需求为桨扇发动机的发展提供了机遇,因此对桨扇发动机进行研究具有一定的经济和环保价值。现今桨扇发动机有多种实现方案。一种桨扇发动机的结构如图1所示。该桨扇发动机采用的3转子结构可以提升发动机的功率,采用的对转桨扇可以抵消一部分力矩。基于以上优点,本文选取3转子对转桨扇发动机作为研究对象。
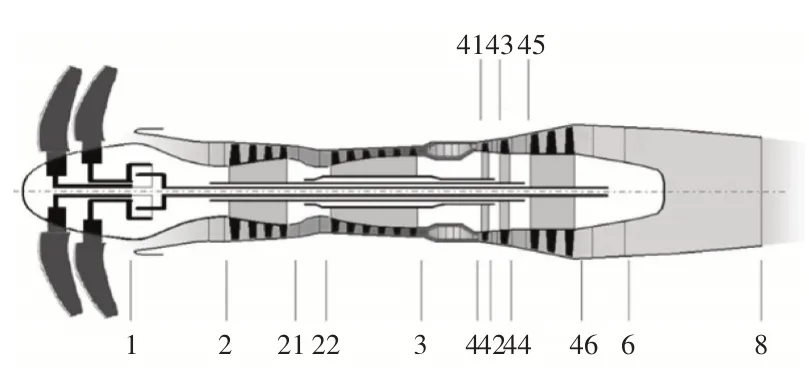
图1 桨扇发动机结构
在飞行状态给定时,发动机控制量确定了其工作状态,桨扇发动机常用的控制量有供油量和前后桨扇桨距角、。对桨扇发动机加速控制计划进行优化就是运用优化算法来求解发动机过渡态中1组最佳的控制序列[]=([][][]),使得发动机可以在最短的时间内从初始状态到达目标状态。要使用优化算法对发动机过渡态进行优化,需将发动机加速过程转化为1个标准的优化问题,而转化的第1步就是确定优化目标和约束条件。由于桨扇发动机的推力绝大部分都来自于前后桨扇叶片产生的推力,为了使桨扇发动机工作稳定,需保证工作时功率涡轮轴转速保持100%不变,不能按传统涡喷、涡扇发动机那样通过转速和推力的一一对应关系来间接确定推力。但桨扇的推力可以很方便地通过转速和桨距角从特性图中插值求得,因此本文直接对推力进行优化。
衡量发动机加速性能最直观的指标就是加速时间,加速时间越短、超调量越小,往往说明发动机的加速性能越好。由于发动机的加速过程是连续的,需要将整个加速过程分割为一系列的静态过程。在每段20 ms的加速过程中,通过优化算法计算当前状态下的最优控制量,使得推力在满足约束的前提下达到当前状态下能达到的最大值。如果加速过程中每个20 ms内的推力都增长到了当前状态下所能达到的最大值,即当前推力与目标推力的差值最小,便可保证整个加速过程的时间最短。依此对目标函数进行转化和离散处理,具体时间最优过程寻优的目标函数为
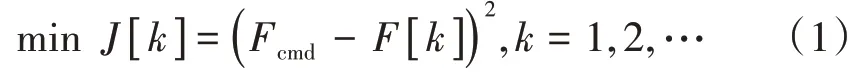
式中:[]为第个仿真步长中的目标函数;为目标推力,在每步中均保持为终态推力不变;[]为第个仿真步长结束后的预测推力。
通过该目标函数即可保证发动机推力在每个20 ms步长中都尽可能地接近目标推力值。
同时,桨扇发动机在加速过程中需要保证高压轴转速、低压轴转速、功率涡轮轴转速、涡轮前温度、高压压气机喘振裕度和低压压气机喘振裕度都处在安全范围内。此外,、、等桨扇发动机的控制量也会受到执行机构调节范围和调节速度的限制。综上所述,桨扇发动机需要满足以下12个约束

式中:、、为高压轴、低压轴、功率涡轮轴的最大转速;为最高涡轮前温度;、为高、低压压气机最小喘振裕度;为发动机最大供油量;Δ为供油量变化速率;Δ为最大供油量变化速率;、为最大、最小前桨距角;、为最大、最小后桨距角;Δ、Δ为前、后桨距角的变化速率;Δ为最大桨距角调节速度。
将桨扇发动机的安全约束经过归一化处理转化为以下14个约束函数

最终得到了最短时间加速控制计划优化问题的标准数学形式

2 AFSA算法
2.1 算法简介
人工鱼群算法主要利用鱼的3大基本行为:觅食、聚群和追尾行为,采用自上而下的寻优模式,从构造个体的底层行为开始,通过鱼群中各个个体的局部寻优,达到全局最优值在群体中凸显出来的目的。人工鱼的3种基本行为简述如下。
2.1.1 觅食行为
觅食行为是鱼群循着食物多的方向游动的行为,是鱼趋向食物的一种活动。人工鱼视野如图2所示。
人工鱼X 在视野内随机选择一种状态X

式中:为人工鱼的视野半径;为0~1之间的随机值。
计算X 和X 的目标函数值Y 和Y ,如果Y 好于Y ,则X 向X 的方向移动1步
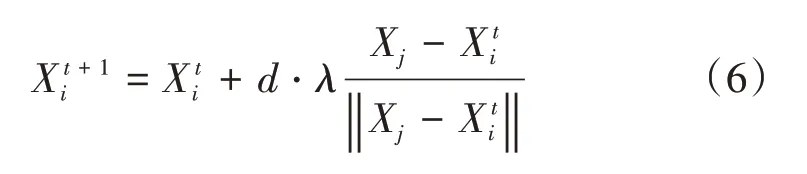

图2 人工鱼视野[16]
式中:为步长。
否则,X 继续在视野内寻找X 并判断是否满足前进条件,寻找次数达到上限后仍未找到X 时,随机前进1步

2.1.2 聚群行为
鱼聚集成群可以集体觅食和躲避敌害,这是鱼在进化过程中形成的一种生存方式。鱼聚群时会遵守2条规则:(1)尽量向邻近伙伴的中心移动;(2)避免过分拥挤。
人工鱼X 搜索视野内的伙伴数量和中心位置,如果>δY (其中为拥挤度因子),则表明伙伴中心位置较好且不太拥挤,朝伙伴中心移动1步,否则执行觅食行为

2.1.3 追尾行为
当某1条鱼或几条鱼发现食物时,附近的鱼会尾随而来,导致更远处的鱼也尾随过来。
人工鱼X 搜索视野内目标函数Y 最优的人工鱼X ,若Y n>δY ,则表明伙伴位置较好且不太拥挤,朝最优人工鱼移动1步,否则执行觅食行为。
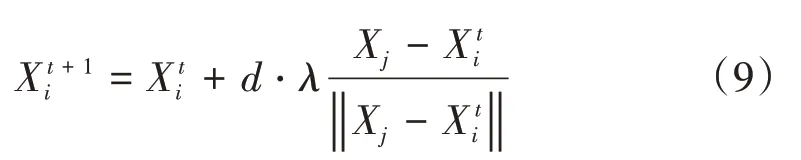
2.2 算法改进
针对算法存在的后期搜索盲目性大的缺陷,文献[16]通过引入双高斯函数对觅食行为进行改进,因文献中通过双高斯函数获取步长调节系数的计算参数过多、过于复杂,本文对步长的自适应调节机制进行简化。另外,由于原始算法无法求解带约束问题,本文参考[15]引入半可行域思想来处理约束。
2.2.1 动态调整视野和步长
视野对人工鱼群算法的行为和收敛性能有较大影响。视野范围较大时,人工鱼的全局搜索性能强并能快速接近最优点,但可能会在最优值附近出现振荡现象,难以稳定;视野范围较小时,人工鱼的局部搜索能力强,可以更精确地接近最优值,但存在收敛速度慢的缺点。
对于发动机这一类强非线性系统,寻优前期应该加强全局搜索能力,在大致定位到最优值的位置后改为加强局部搜索能力。因此在算法运行前期,为了增强算法的全局搜索能力和收敛速度,采用较大的视野和步长,使人工鱼可以在大范围内进行粗搜索;随着搜索的进行,逐渐减小视野和步长,最后算法在最优解附近进行精细搜索,从而提高算法的收敛速度和寻优结果的精度。
视野和步长的动态调整策略为

式中:为调节系数,需满足前期从1开始缓慢减小,后期快速减小直到接近0,根据文献[14]中一些算法实例,本文采用指数函数对进行调节

式中:为当前迭代次数;为最大迭代次数;为大于1的整数。
视野的初值选取为/ 4(为搜索宽度),步长的初值选取为/ 8,最小视野半径=0.05,最小步长=0.005。
2.2.2 对觅食行为的改进
在人工鱼群算法的觅食行为中,人工鱼会随机选择一种状态,如果该位置优于当前位置,则向该方向移动1步,但在该方式下人工鱼只能前进不能后退,因此对人工鱼的移动方式加以修改

2.2.3 对约束问题的处理
由于发动机参数有严格的限制条件,在寻优时必须对约束条件进行处理。为了最大限度地发挥发动机性能,在寻优时需要使发动机的工作点尽可能地接近限制边界。如果只是简单地让可行解无条件地优于不可行解,易使寻优结果远离边界,陷入局部最优或者寻不到最佳性能点,因此本文引入半可行域的概念对约束进行处理,通过保留一定比例稍稍超过约束边界的人工鱼样本,来保证寻优算法具有搜寻到边界附近最优点的能力。
同时,由于发动机各物理量的数量级相差较大,直接使用物理量计算不利于各约束间的比较,影响寻优计算时的准确性。因此需要对各量进行归一化处理。
对于归一化后的不等式约束极值问题的标准形式为

引入评价人工鱼与约束边界接近程度的函数()

对于1个给定的正数,有()≤,则将该人工鱼样本定义为半可行点,将其保留并参与后续的优化过程;对于()>的人工鱼样本则直接舍去,并用重新生成的人工鱼样本来代替。
为了保证人工鱼样本集合中保留一定比例的半可行点,引入对阈值的自适应调节机制

式中:为半可行点在所有样本中所占的比例;为要保持的半可行点所占比例的目标值;为阈值每次动态调整的步长。
最终筛选样本时从优到劣排列的标准为:
(1)可行点严格优于半可行点;
(2)可行点间目标函数值更佳的为优;
(3)半可行点间()值较小的为优。
2.3 算法步骤
对人工鱼群算法进行改进后,算法求解步骤如下。
定义鱼群规模、初始可视域半径、拥挤度因子、初始移动步长、最大尝试次数、最大迭代次数、半可行点判定阈值、半可行点比例和阈值调整步长,在约束范围内随机生成人工鱼群样本;
计算初始鱼群每个个体的目标函数值,将最优人工鱼的位置和目标函数值记录在公告板中;
分别执行聚群行为和追尾行为,如果满足移动条件,则向2种行为中更优的方向移动1步,如果均不满足移动条件,则执行觅食行为;
评价新一代鱼群的所有个体,如果某个体目标函数值优于公告板值,则更新公告板上最优解的位置和目标函数值;
计算半可行点在鱼群中的比例,按结果调整半可行点判断阈值;
如果前后2代的最优人工鱼个体目标函数值没有满足一定的精度要求或计算代数没有达到最大次数,返回到步骤3;
寻优结束,输出结果。
2.4 算法验证
为了验证改进后的人工鱼群算法的寻优性能是否优于标准的人工鱼群算法,本文选取表1中的标准测试函数进行验证。验证算法的具体参数为:=100,=1,=0.618,=0.05,=100,=1000,=0.01,=15%,=0.005。

表1 标准测试函数
用2种算法对每个标准测试函数分别测试5次,记录寻优结果的最优值、最差值、平均值和平均优化代数,并与文献[16]中同测试函数下的双高斯法改进结果进行对比,文献中鱼群算法参数与前2种算法的一致。仿真环境为:Intel®Core™i5-8300H CPU@2.30 GHz,16 GB内存,Win10 64位操作系统,VS2010编程。具体寻优结果对比见表2。
从表中可见,3种算法的最优解均能在约束范围内接近理论最优值0,可以在一定程度上验证本文算法程序的正确性。与原始AFSA相比,改进后的AFSA平均迭代次数减少幅度较为明显,平均寻优结果精度的数量级提升较为明显,说明改进后的AFSA较原始AFSA具备更快的收敛速度和更高的收敛精度。将本文改进AFSA寻优结果与文献[16]中的双高斯改进AFSA进行对比发现,本文算法虽然经过简化,但精度依然很高,平均迭代次数与文献[16]中的结果相近,且对于测试函数1,本文算法平均迭代次数明显小于文献中的结果。
3 最优加速控制计划的获取
以桨扇发动机在飞行高度=0 km时的加速工作状态为例,对于其他工作点,只需在模型中修改相应高度、马赫数的数值即可。在加速时,飞行员通过推油门杆来设定目标推力值,选取发动机的一种典型工作状态:从巡航状态(推力为最大推力的60%)加速到最大推力状态(100%推力)的场景进行优化。分别运用改进的AFSA和SQP算法对该过程的加速控制计划进行优化,得到在加速过程中的推力、各控制量和典型参数随时间的变化,如图3~6所示。

表2 改进AFSA和AFSA、NAFSA[16]的寻优结果对比
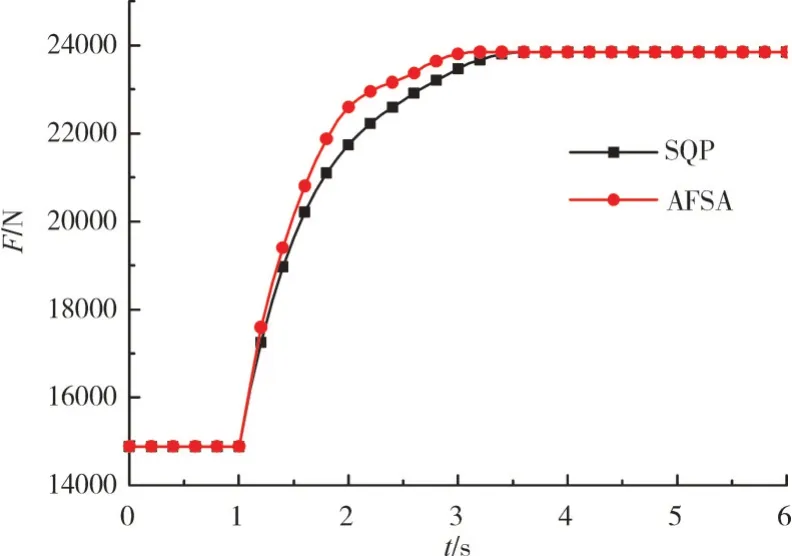
图3 在加速过程中推力随时间的变化

图4 在加速过程中桨距角随时间的变化

图5 在加速过程中供油量随时间的变化


图6 在加速过程中典型参数随时间的变化
从图中可见,改进AFSA和SQP 2种算法均可保证优化后的控制计划在整个调节范围内满足约束要求。
将2种算法得到的桨扇发动机时间最优加速过程总时长和寻优程序总计算时间进行对比,结果见表3。

表3 算法效率对比 s
从表中可见,改进AFSA计算出的时间最优加速控制计划的加速时间比SQP的结果缩短21.8%(0.58 s),说明改进AFSA的全局寻优能力更强,在寻优时可以更加精确地搜索到每个步长中满足约束要求的最大推力;但SQP算法在计算代数更多的前提下,总计算时间仍然短于改进AFSA算法,说明在计算速度上,基于梯度的数学基础更严密的SQP算法更胜一筹。
4 结论
通过引入自适应调节策略和半可行域对AFSA算法进行改进,提高了收敛速度和寻优精度,实现了对带约束优化问题的求解。
将改进AFSA算法应用于具有多个可调变量的桨扇发动机加速计划优化中,得到的控制计划加速时间比SQP算法的缩短21.8%(0.58 s),证明了该算法具有更强的全局寻优能力。
综上所述可知,改进AFSA算法具有优秀的非线性全局寻优能力,适用于桨扇发动机过渡态加速计划的优化。

