基于思维可视化构建小学减负增效新课堂的策略探讨

作者简介：余雅清（1992～），女，汉族，福建厦门人，厦门第二实验小学，研究方向：小学数学。

摘 要：小学数学阶段，学生对知识的表达空洞、不直白，思维内隐、晦涩，最终在知识的理解掌握方面表现不佳。文章基于当前教学现状对相关问题产生的原因进行分析，在前人研究的基础上，为构建减负增效的新课堂提出思维可视的方法。

关键词：思维可视;思维发展;减负增效

中图分类号：G623.5 文献标识码：A 文章编号：1673-8918（2022）18-0001-05

一、引言

課堂上知识点和习题讲解后，笔者常常想要得到学生的反馈，于是问道：“还有不清楚的吗？”学生往往是清一色地回答：“没有，懂了。”就算个别诚实的学生回应还不大明白，再讲解后已经理解，可是一旦受到变式应用练习的冲击，经常还是大面积的遭殃，许多题目的错误率比预想的要高得多。没有标尺，没有量表，如何精准衡量和把握？虽有思考，但学生思维过程很隐晦，知识的加工程度不同，无法确定知识掌握水平，更难有的放矢地帮助学生。课堂的时间短容量大，学生如何轻松牢固地掌握重难点，及时内化和拓展思维？教育部出台“五项管理”，减负再次被广泛关注，如何构建有效课堂，成为笔者经常思索的一部分。

其实这是学生内隐思维导致知识掌握不佳的表现。内隐思维是游走于脑袋里的想法，经常是一闪而过、不具体、不全面的思考，这种思考往往是不经过表达、记录和动态生成的，更多存在于一种被动式地接受学习模式中，而非主动式探索，这样的思维经常被指向“似懂非懂”。学生要提高掌握知识的效率，需遵循理解、巩固保持与应用练习的规律进行。内隐思维导致知识掌握不佳，就是以被动式学习的方式参与，思维内隐模糊，思考浅薄片面，出现理解新知上不全面，巩固知识时没效果，进而在应用领域手足无措、错误率极高的现象。

内隐思维导致知识掌握不佳主要有以下特点：

①能理解部分知识点，但处在一个似懂非懂的境地，好像听得懂，但又说不清道不明。

②难以与本身的已有知识网络勾连，新知识未能纳入已掌握的知识系统，已有知识未获得扩大和更新。

③在变式训练和应用练习上，手足无措，错误率极高。

二、存在问题的原因分析

基于存在的问题，笔者进行充分的分析讨论，力求抓住问题的核心，探求其本质原因。探求问题的本质主要是从客观和主观两个方面着手。客观上和实际教学的材料内容有关，主观上与教师和学生有关。

（一）形象向抽象过渡期，思维特点受限

小学阶段是学生具体形象思维向抽象逻辑思维过渡的关键期，尽管发展逻辑思维成为主要任务，但学生始终脱离不开直观的支撑和直接的经验。特别是面对抽象的问题常常表现得迷茫困惑，只有以具体形象的事务作为切入点，问题才能有所突破。

（二）留痕习惯规范欠缺，少主动不科学

学生年龄尚小，他们偏向天马行空，喜欢用自己的方式表达思维，但往往他们的方式还不够科学有效率。日常理解知识和练习过程中，他们是存在惰性的，在过程表述方面能省则省，不愿意多花时间呈现自己的思考过程，一旦教师对“可视化思维”提出一些规范要求，他们的反应一般是较为抵触，不愿接受。

（三）留痕习惯指导欠缺，心有余力不足

在实际教学中，教师会忽略留痕习惯的培养，在画图、操作、言说、记录方面的指导不够细致，未能及时发现和反馈学生的问题，学生只是为了做而做，不知道这些工具是为思维发展服务的。等到学生独立思考问题时，无从下手，不知道借助什么工具分析，如何开始分析，怎么进行严谨的分析。教师有时候有了自己的教学主张，但在推进过程中或是后续学习中难以坚持贯彻和执行，教学压力下，往往“思维可视”的指导就成为牺牲品。久而久之，又打回原形，还是原来的教和原来的学。

（四）受到学习材料牵制，重结果略过程

在部分学习材料的编拟中，体现出精简的过程，更重视结果的达成，从而忽略了过程的产生，会给学生错误导向。然而部分学习材料考虑学生的思维特点，能够契合学生年龄特点来编制，但是在呈现方式上，无法多元呈现，例如对话、图像、动态图，甚至动画、视频等，学生感受不深，无法深刻体会知识内容的本质，往往只见树木不见森林，只记结论不学方法。在部分练习材料中，考查的方向则偏向于应用知识的结论方面，而非知识的过程方法，学生也顺势代用公式，生搬硬套，不考虑思维方法。

三、前人的研究成果

文章旨在利用“思维可视化”的方法介入学生的知识掌握过程，弱化思维内隐的弊端，在理解、巩固保持的环节中加以监控和干预，帮助学生形成良好的思维习惯，提高知识掌握水平，以达到最大限度应用知识，拓展思维，发展能力的目标。

在中国知网（CNKI）数据库以主题为“小学数学思维可视”进行了精确查找，共检索到136篇文献，其中博士论文1篇，硕士学位论文10篇，期刊119篇，国内会议6篇，研究发展呈现出逐年上升的态势。

刘坤在《思维可视化导学案在小学数学教学中的运用实践》一文中提出：让学生掌握思维可视化学习方法要有“识图—制图—用图”三个阶段。此外，还提出了运用思维可视化需要注意的事项。

季容臻在《基于“思维可视化”的小学科学探究教学策略》一文中提出，“思维可视化”是一种认知策略，根据儿童思维发展的局限性而提出。“思维可视化”包含两种表达形式：“可视思维”“有声思维”，其中“可视思维”，即将抽象知识或事物通过一定手段的转化，使之变得具体、直观。

张齐华提出要善于调动学生的多重感官，创新教学路径，用直观的图形表征抽象的思维，在动手操作与实践中体现思维的过程，在语言表达中外化学生的思维，通过“画”“做”“说”参与思维的发生、发展和过程表达中。

从有关研究可以看出，思维可视化的教学能够促进学生的思维发展，促进学生的学习，提高教学有效性，因此思维可视化受到广大研究者的高度关注。但思维可视化研究应用到小学数学学科的研究较少。小学阶段是学生思维能力培养和发展的关键时期，且数学是一门依靠思维的学科。因此，小学数学思维可视化教学有待于进一步的研究。基于前人研究成果，文章所研究的思维可视主要涵盖：直观的图形表征、探究式的动手操作和精准的数学语言，而数学语言又通过文字和口头两种方式进行表达和传递。

四、思维可视化策略建议

随着数学教学的发展，培养数学核心素养如今受到前所未有的重视。在现阶段，拓展学生的数学思维成了数学教学的根本任务。数学学习本身就是抽象的晦涩的，其思维更是内隐的不可见的，如何破解思维这个神秘的“黑匣子”，就需要教师利用有效的手段，将内隐逻辑具象化，实现思维可视化，让教师能及时地跟踪，有效地把握学习情况，学生能了解自己的掌握情况，也能评价其他同学的学习情况，达到思维的提升，最终实现核心素养的达成。

要想实现清晰追踪学生学习情况，及时跟进和调整的有效课堂，就要通过一定的策略使得学生思维输出可视化。

（一）“画”得精准，用形象解释抽象

美国数学家斯蒂恩曾说：“如果一个特定的问题可以被转化为一个图形，那么，思想就整体地把握了问题，并且能创造性地思索问题的解法。”图示法的使用，无形中渗透着数形结合、几何直观、数学模型等数学思想方法，对数学学科核心素养的培养有重要意义。

1. 示意图演绎生活情境

示意图能大体上描述或表示物体的形状、相对大小、物体与物体之间的关系，低年级的学生以具体形象思维为主，将抽象的文字信息转化成便于理解的示意图，有利于化解抽象问题与学生思维本身固有的特点之间的矛盾。正如心理学家刘范所言：“即使是只要求儿童进行对抽象的数进行运算的项目，儿童往往会借助直观的图像来求解答;当解题遇到困难时，这种现象更为常见。”

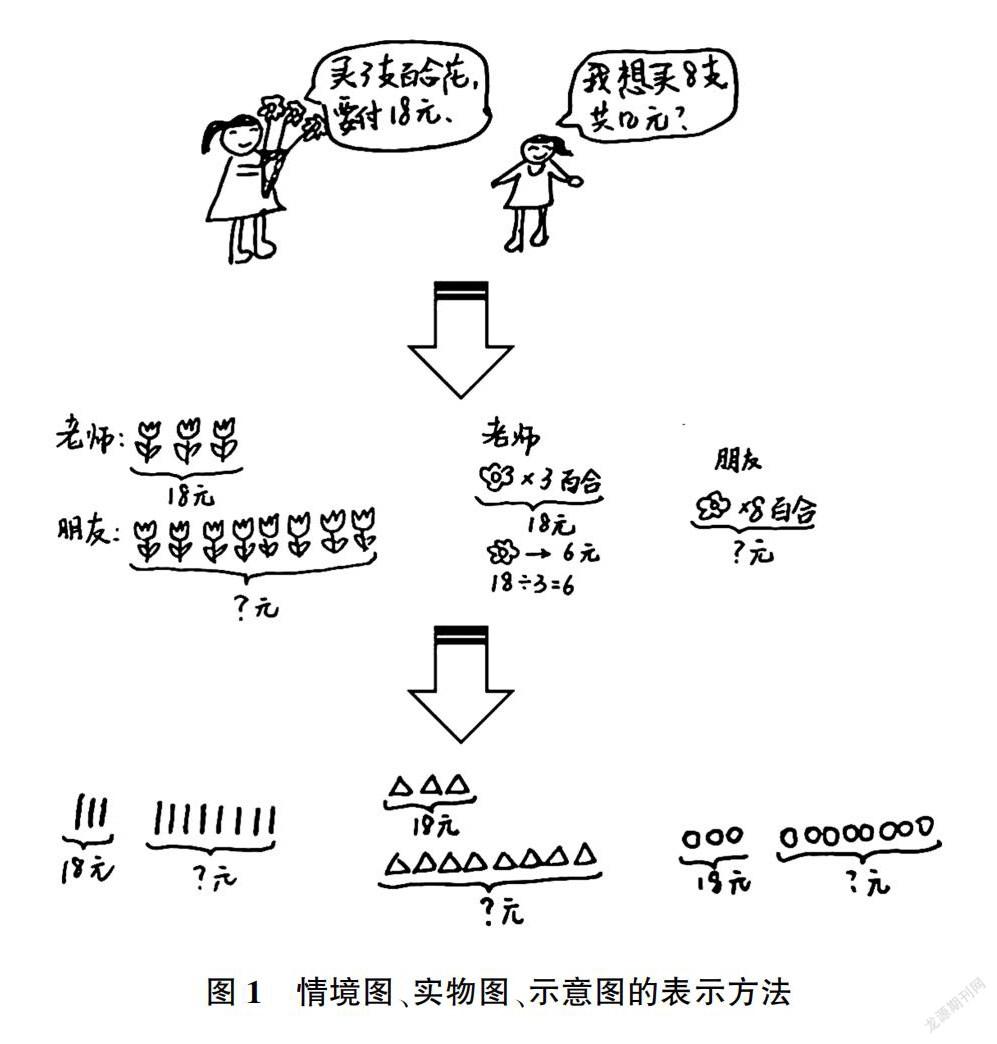
例如，执教有关“归一”的解决问题时，面对“老师买了3枝百合花，付了18元，老师的朋友，也想买8枝同样的百合花，老师的朋友要付多少钱？”引导学生用画图的方式表示已知条件和问题。学生经历了画图过程，从具体的情境图到实物图，再到示意图，带领学生在对比中优化简明的画图方法。更重要的是，要求人人能解释算式的道理，18÷3算的是一枝百合花的价格，在图里用一个○表示，要求8支百合花的价格，就是8个○的总和（如图1）。

图1 情境图、实物图、示意图的表示方法

学生通过亲身试水画图，感受画图的优越性和必要性，自然而然地演绎了稍复杂的情境，再通过问题导向，增强“读图”的意识和能力，分析数学信息，明晰数量关系，勾连图与式。在归纳总结中建立归一的数学模型，一系列的思维活动悄然发生，教师也能在一幅幅图中把握学情，启发思考。

2. 线段图辨清不同情境

线段图是由几条线段组合在一起，用来表示应用题中的数量关系，帮助学生分析题意，解答问题的一种平面图形。线段图在中年级开始引入使用，其直观形象的特点，能将抽象信息进行再创造，从而达到问题解决的目的。

例如，在《画线段图解决问题》一课中，“红花是黄花的2倍，白花是黄花的3倍，三种花一共有36朵，黄花有几朵？”和“一根绳子剪掉了全长的一半还多10米，还剩30米，这根绳子长多少米？”这两个例子，刚出示时学生感受并不深，甚至习惯用以往一条线段表示，但是通过对比，就能进一步提炼得出：总体与部分关系，通常画成一条线段，而不同量的关系通常需要画成多条线段，便于比较（如图2）。

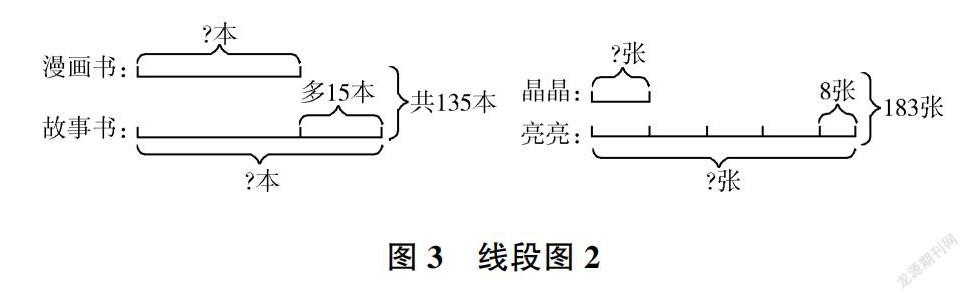
随着教学推进，呈现问题：“漫画书和故事书一共有135本，故事书比漫画书多15本，问漫画书和故事书各有多少本？”根据“故事书比漫画书多15本”这一关系句可以马上确定出标准量是漫画书，再进一步画出故事书。而在稍复杂的情境下“晶晶和亮亮一共有183张卡片。亮亮的卡片数量是晶晶的4倍多8张，两人原来各有卡片多少张？”重点分析“亮亮的卡片数量比晶晶的4倍多8张”，也能得出标准量是晶晶的卡片数量。不管是和差问题还是倍数问题，都要根据关系句画图，而且要先画标准量再画比较量，还要标清数据，理清数量关系（如图3）。

线段图呈现思考过程，可能是不完整或是不清晰的，但是，线段图这种可视化的思维输出，教师看得见，一次次把握重要节点，适当点拨，及时归纳，学生对问题的把握越来越清晰，后续学生在运用图形解决问题上不仅有方向了，而且也有方法了。

3. 矩形图解开复杂情境

越到高年级，用矩形图解决问题的需求开始产生。根据题意画出矩形，可用矩形的长表示一种量，用矩形的宽表示另一种量，面积表示这两种量的积的关系，这样可以把抽象的数量关系变得具体形象，便于寻找解题线索。

例如，在执教《画矩形图解决问题》时，面对较直接的面积问题，长宽的对应关系很明显，但是对不显著的问题情景，则需要重点明确长表示什么、宽表示什么，在图与式之间建立勾连，打破学生原有的不熟悉和不习惯。继续丰富矩形图的内涵，并非只能适用于“长×宽=长方形面积”类型，也能作用于“每份数×份数=总数”，甚至是“单价×数量=总价”“速度×时间=路程”等一系列两个数的积的数量关系的模型中。将各种相关数量关系融汇在一起，理解长、宽所表示的含义，逐渐会发现图示法的优点——利用图示法可以解决一系列的数学问题（如图4）。

这样的过程就是重要的数学建模，模型建立，再延伸到遇到复杂的数学问题也能迎刃而解了。通过绘制矩形图，学生的思维拓宽，層次拔高，而且提高问题解决的能力，增加学习的自信。

执教过程中，应结合学生的年龄特点，将各种画图方法融入日常教学中。当学生遇到困难时，能根据问题情境灵活选择画图的策略，在“画”中分析信息和问题之间的关联，用形象易感知的手段辅助解释抽象的问题情境，就能有效突破思维瓶颈，有利于问题解决。

（二）“做”得具体，借操作提升思考

美国教育家杜威提倡“从做中学”，或者说，“从经验中学习”。在他看来，教学应从学生的经验和活动出发，使学生在游戏和工作中获得知识和能力。学生个人的操作经验是最有说服力的，比起直接的教给，学生显然理解得更深刻和全面。

例如，在《平行四边形的面积》一课中，引导学生注意整体的全局意识，推导公式是一个过程，不是为了转化而操作，而是为了后续的找联系和推导进行铺垫。清晰的思路，便于指引学生进行有向操作，所有的操作活动变得主动积极、有指向、有目标，“动”中会思考着怎么实现转化，“动”后还会想着如何找联系、推公式。因为看得到学生的动态操作过程，就能发现学生活跃的思维贯穿活动中和活动后，避免了操作活动与主动思考的割裂，实现了操作的高效性，学生的思维也跟着推进和发展。

（三）“寫”得多样，依留痕全盘考虑

写这种简单易操作的手段，也是思维留痕的重要手段，如何有效地写、写到什么程度就显得尤为重要。有效写出，就有发展思维的可能，完整写出，就是发展全面思维的基石。《分数除法（除数是整数）》中提到：“是不是所有的分数除以整数都可以转化成乘整数的倒数。请你们以6/7÷4为例进行说明。”用画图的方法学生已经觉得麻烦，不适用，所以有用说理解释的，“6/7÷4相当求6/7的1/4，就是把6/7平均分成4份，取其中的一份”，还有利用商不变的性质来转化。（如下5）思维多样化、全面化全在可视中追踪和引导，课堂得以呈现丰富、有层次的形态。

6/7÷4

=6/7×1/4÷4×1/4

=6/7×1/4÷1

=6/7×1/4

6/7÷4

=6/7×7÷（4×7）

6/7÷4

=6/7×7/6÷4×7/6

（四）“说”得清晰，靠逻辑改善混乱

1. 大问题牵引，给学生整理语言的机会

知识拒绝“咀嚼”完了再给学生，设置大问题，有利于引导学生全面思考问题，完整经历探究过程，从而避免接受支离破碎的知识，也减少了浅度思维。例如，在教学《平行四边形的面积》时，在课堂的开始就用短平快的方式问道：“我们怎么进行平行四边形面积研究呢？你有想法吗？”学生的思考量大，不仅要考虑研究的某一个环节，还要思考如何一步步地推进，还可以回忆以前的相关经验找两者不同。这样把繁杂的知识点用统一归整的问题牵连起来，给学生留足时间思考讨论，也给学生整理思路语言的机会，全面的、深度的思维也在问题的驱动下得以绽放。

2. 深入式对话，让学生调整语言的契机

师生、生生之间的深入对话能打通教学中的固有状态，即“似懂非懂”的状态。只要多追问一句，“你是怎么想的？”“说说你的理由。”放低自己的姿态，更多地亲近学生，走进学生，深挖学生资源，“能说得更具体点吗？”“你能再完整地说一遍吗？”其实这样的过程教师已经完整跟踪到学生的掌握情况，而且已经在纠正学生对知识的理解疏漏。学习不是浅尝辄止，更不是人云亦云，教学中多留出一部分时间，多追问，多质疑，给予学生评价反馈的机会。如此推进，不仅能在分享、对话、质疑、辩论中求同存异，还能建构知识架构，思维就在这样开放的、有深度的对话中悄悄展开并升华。

学生利用以上的手段，将内隐逻辑具象化，实现思维可视化，使得教师能及时地跟踪，有效地把握学习情况，学生能了解自己的掌握情况，也能评价其他人的学习情况，达到思维的提升，最终实现核心素养的达成。

知识类型的不同决定了教学方法的差异，但使思维可见，通过以上的“画”“做”“写”“说”的方式，让教学有所依，在精心设计的活动下，学生的思维正悄然走向高阶，也符合了当下对教育的追求：教得少而精，学得深而广。减负增效的新课堂，将使得教育质量提高，学生兴趣提升，教育氛围融洽。

参考文献：

[1]史宁中.《数学课程标注（2011年版）》解读[M].北京：北京师范大学出版社，2012：28，120.

[2]季荣臻.基于“思维可视化”的小学科学探究教学策略[J].江苏教育研究，2018（2）：47-50.

[3]刘坤.思维可视化导学案在小学数学教学中的运用实践[C]∥《教师教学能力发展研究》科研成果集（第十一卷），2017，11.

[4]曹小兰.“可视化”教学，让学生的数学思维看得见[J].小学教学参考，2017（26）：47.

[5]张齐华.“思维可视化”视域下小学数学课堂之重建[J].江苏教育，2017（25）：48-50.