风震联合作用下高层建筑主体结构和玻璃幕墙的性能研究
任重翠,李建辉,唐 意,刘军进,严亚林,郝 玮,孙 超
(1. 建研科技股份有限公司,北京 100013;2. 建筑安全与环境国家重点实验室,北京 100013;3. 国家建筑工程技术研究中心,北京 100013)
《关于加强超高层建筑规划建设管理的通知》[1]是住建部为了推进城市发展而颁布的,该通知使我国超高层建筑建设日趋下降,因此,普通高层成为城市主流的建筑形式。一栋普通高层建筑既包含内部主体结构,又包含外部围护结构。其中,起美观和围护作用的玻璃幕墙在高层建筑中作为附属结构,对主体结构的影响较弱[2],在设计中常以等效荷载的方式进行施加[3],不作为实际构件进行建立。然而,在地震或风等灾害荷载作用下,主体结构虽然具有一定的安全性[4−5],但玻璃幕墙等非结构构件的破坏常会产生更为严重的次生灾害,并对灾后救援产生重要影响。如1994年1月17日的美国加州北岭地震[6],造成大量结构和非结构构件破坏,上千人受灾,经济损失达300多亿美元;2017年8月23日从广东省珠海市登陆的台风“天鸽”,致使受伤和死亡人数过百,经济损失高达83.1亿元。
因此,有必要开展考虑玻璃幕墙等非结构构件的总体结构分析。而目前有关主体结构与玻璃幕墙的非线性分析及两者的相互影响研究较少,多为幕墙构件[7−8]、局部单元的线弹性分析[9−10]及相关试验研究[11]。
内部结构作为高层建筑的主体在地震作用下的响应较大;而玻璃幕墙作为附属结构,主要受风荷载影响。当两者联合建模计算时,需进行风、地震荷载作用下的全面分析。因此,可在风、地震单独作用的情况下,进一步进行风震联合作用研究。目前,关于风震联合作用的研究已成为土木工程领域的热点,如2019年刘杨等[12]采用地震需求分析法研究了一栋钢管混凝土框架-防屈曲支撑结构的易损性;2020年周颖等[13]以一栋580 m高的超高层建筑为例,分析了风震耦合作用下的结构抗振可靠度;2022年任重翠等[14]对一栋300.5 m高的超高层建筑进行了风震耦合作用分析。可见,对普通高层的主体结构与玻璃幕墙在风震联合作用下的研究分析仍较为匮乏。因此,对普通高层建筑开展风、地震单独及联合作用下的主体结构与玻璃幕墙非线性响应分析,会对高层建筑结构的抗灾设计和研究分析提供一点新思路。
本文依据《建筑结构抗倒塌设计规范》[15]对非结构构件的建模要求,将玻璃幕墙建入一个98 m高的高烈度区框架-核心筒结构,形成总体有限元分析模型。基于场地条件选取三组地震波,并通过1∶440缩尺模型风洞试验获得不同重现期、持时约600 s的风压荷载值。采用能够反映结构受力过程的动力弹塑性分析方法,研究主体结构和玻璃幕墙的相互影响及两者在风、震单独和联合作用下的性能变化,从而为高层建筑主体结构与玻璃幕墙的抗震、抗风设计提供一点参考。
1 结构设计信息
1.1 框筒结构
框筒结构[16]的高度为98 m,共24层,层高为:F1层6 m,F2层~F24层4 m。结构平面为44 m×44 m的正方形(图1),对应高宽比为2.2;核心筒是一个矩形平面,大小为21.8 m×20 m,高宽比4.5。外框柱子之间及与筒外墙的距离分别为8.8 m和12 m。

图1 标准层平面图Fig. 1 Structure typical plan
抗震设计参数:8度(0.2 g)设防、丙类,地震分组为第一组,III类场地,Tg为0.45 s。
设计风荷载:地面粗糙度为B类,重现期10年、50年、100年及1.1倍100年的风压值分别为0.4 kPa、0.65 kPa、0.75 kPa及0.825 kPa。
采用SATWE软件设计得到的墙、柱构件截面尺寸及混凝土强度等级列于表1。

表1 墙柱构件设计信息Table 1 Design information of structure members
结构梁板为现浇体系,混凝土为C30。楼板厚度:核心筒外110 mm,核心筒内110 mm 、130 mm。
小震下结构设计基本信息列于表2,可见结构层间位移角小震下为1/864,远大于风荷载下的1/4344,表明本结构为地震荷载作用控制。结构整体计算指标均能满足现行规范的设计要求。

表2 结构设计基本信息Table 2 Basic information of structural design
1.2 玻璃幕墙
玻璃幕墙的横梁、立柱为铝制框材,截面为管材□300 mm×120 mm×10 mm;玻璃单元为单片厚度为8 mm的双层中空玻璃。玻璃幕墙单元的平面长度尺寸约为3 m。铝材和玻璃对应的强度标准值[2]分别为172 MPa、50 MPa。
2 损伤与坠落分析方法
2.1 结构材料属性
钢筋和铝材的应力-应变关系如图2所示,可见刚度在应力应变循环过程中无退化。材料极限应变和强屈比为0.025、1.2。

图2 钢筋和铝材的应力-应变关系图Fig. 2 Stress-strain relationship of steel and aluminum
混凝土模型见图3,其中梁柱混凝土自行编写,材料轴心抗压、抗拉强度按《混凝土结构设计规范》(GB 50010−2010)[17]表4.1.3确定。
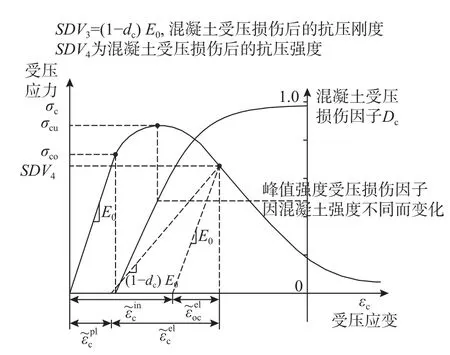
图3 混凝土弹塑性损伤模型Fig. 3 Elastoplastic damage model of concrete
玻璃[18]采用图4所示的脆性断裂模型[19],该模型采用最大主拉应力破坏准则。
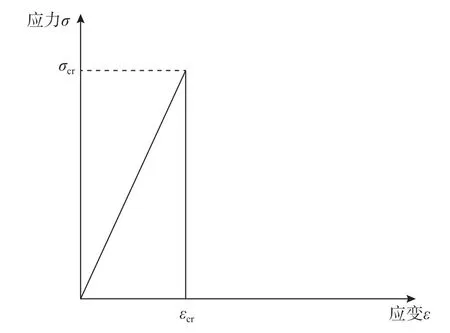
图4 玻璃应力-应变关系Fig. 4 Stress-strain relationship of glass
2.2 构件有限元单元
在分析中主体结构梁、柱、幕墙横梁、立柱采用铁木辛柯梁单元模拟(图5(a));剪力墙、连梁、楼板和玻璃采用减缩积分分层壳单元模拟(图5(b))。

图5 相关构件有限元单元Fig. 5 Finite element of components
玻璃单元与横梁、立柱之间的连接关系较为复杂,如玻璃边缘和镶嵌槽之间存在间隙,结构胶具有一定的厚度和变形能力等。以往研究,常将玻璃单元与支撑构件间简单设置为固接或铰接关系,这很难准确反映它们之间的相互作用。因此,基于受力和设计需求,专门研究了可指定多方向刚度和阻尼比的多自由度连接单元,来模拟玻璃与横梁、立柱之间的复杂连接关系[15](图5(c))。
2.3 非线性因素的考虑
分析过程考虑了施工模拟,通过设置单元生死的方法,按照建造过程先施工主体,再施工横梁、立柱,最后施工玻璃幕墙和连接单元,如图6所示。同时考虑了几何“ P-Δ ”非线性、大变形等非线性效应。

图6 结构总体有限元分析模型Fig. 6 Total finite element model of structure
3 损伤与坠落分析研究
3.1 模型校核
主体结构及加设玻璃幕墙单元后的模型校核根据《建筑结构抗倒塌设计规范》(CECS392:2014)[15]第5.1.4条进行。
首先,进行了结构质量、周期和振型对比,如表3和图7所示。可见,加设幕墙单元后结构的质量略增、周期略小、振型不变,表明玻璃幕墙对主体结构质量、周期和振型影响较小。

图7 结构前3阶周期及振型Fig. 7 The first three vibration periods and modes of structure
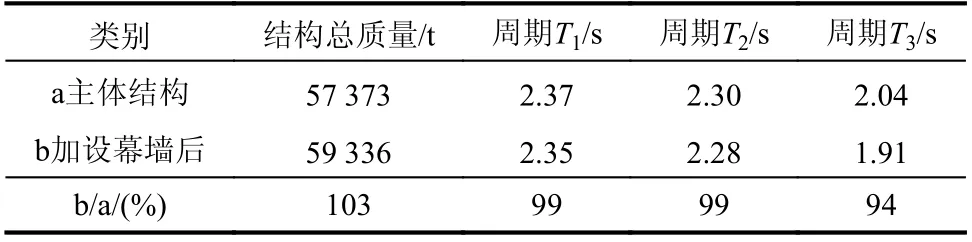
表3 结构质量、周期对比Table 3 Comparison of structural mass and periods
然后,根据《建筑抗震设计规范》[20]的要求,选择一组人工波(图8)。按三向(主向∶次向∶竖向=1∶0.85∶0.65)输入到结构模型中进行大震弹塑性分析,其中峰值加速度为400 Gal。
图8 人工波信息Fig. 8 Artificial wave information
计算得到的结果列于表4和图9,可见,考虑玻璃幕墙的结构顶点位移有所减小,结构基底剪力和最大层间位移角的变化较小。

图9 大震弹塑性计算结果对比Fig. 9 Comparison of elastoplastic analysis results under rare earthquake

表4 大震弹塑性分析计算结果对比Table 4 Comparison of elastoplastic analysis results under rare earthquake
本节分析表明:作为围护结构的玻璃幕墙,对主体结构在地震下的反应和屈服情况影响较小,可以达到规范的设计要求。因此,在后续分析中主体结构的基底剪力和变形等指标可基于主体结构构件给出。
3.2 地震作用下计算结果
为研究主体结构和玻璃幕墙在地震作用下,非线性响应随地震强度增大的变化情况,根据规范[20]选波要求,在图8所选人工波基础上,如图10所示选择了两组40 s的天然波,以峰值加速度400 Gal、510 Gal进行大震和超大震弹塑性时程分析。

图10 两组天然波反应谱曲线Fig. 10 Response spectrum curves of two natural waves
计算结果由表5、图11给出,可见,随地震动强度的增大,主体结构的非线性响应和玻璃幕墙的破坏情况均增大。

表5 地震下主体结构整体指标计算结果Table 5 Main structure index results under earthquake
因核心筒剪力墙出现一定塑性损伤,结构基底剪力的增长低于加速度之比(如b1/a1列中的105%、102%、121%低于127.5%);反映结构变形的顶点位移和最大层间位移角增幅高于加速度增幅,如b2/a2和b3/a3列,尤其是人工波作用下最大层间位移角由1/125增至1/33,表明结构出现不可恢复的变形,面临倒塌。
因峰值加速度为400 Gal时,三组地震波中仅人工波作用下玻璃幕墙发生了大面积脱落,其他两组天然波作用下玻璃幕墙未发生破坏,因此,后续以人工波的计算结果进行说明。
图11(a)~图11(c)玻璃幕墙的破坏位置表明:平行地震作用主向的玻璃单元容易发生破坏,垂直地震作用主向的玻璃单元较为安全。
3.1节的分析已表明:主体结构受玻璃幕墙的影响很小,而玻璃幕墙受主体结构的影响及两者的变形关系有待进一步研究。因此,参考文献[14]中的方法,按图12变形关系图,进行总体模型中主体结构和玻璃幕墙的层间变形及对应的层间位移角关系求解。

图12 主体与幕墙的变形关系分解图Fig. 12 Deformation relation decomposition diagram of main structure and glass curtain wall
按式(1)和式(2)可计算得到总体和主体结构的层间变形:

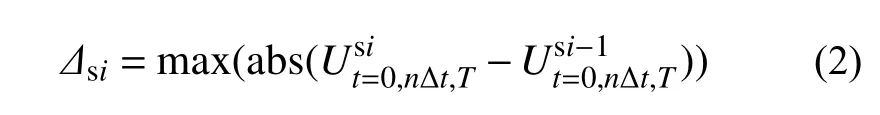
式中:Δi、Δsi为第i层总体、主体结构层间变形;t、Δt为作用时刻、时间间隔;n为正整数;T为结束时刻;0,nΔt,T为第i层的变形时程。
然后,根据式(3)和式(4)可计算得到第i及i−1层玻璃幕墙自身的变形时程:

进而将相邻楼层的时程做差,按式(5)获得玻璃幕墙的层间变形:
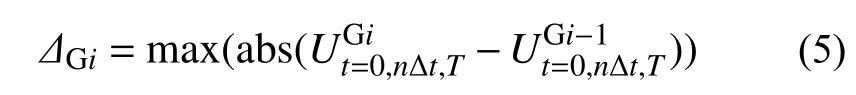
最后,按式(6)所示的层间位移角θi与层间变形Δi、层高hi关系,可求解得到总体、主体结构和玻璃幕墙的层间位移角:

图11(a)~图11(c)表明:玻璃幕墙的破坏位置较为离散,因此为便于对比,后续变形分析以四个外框角柱(图1所示)作为参考点。结果由图13给出,可见,大震作用下主体结构的层间变形,在玻璃幕墙未坠落前大于玻璃幕墙的自身变形。对应400 Gal、510 Gal地震强度,有代表性的中部F12层~F14层玻璃变形占总体层间位移角的比例为30%~32%、20%~22%,对应主体结构层间变形为玻璃幕墙自身变形的3.0倍~3.4倍、4.1倍~4.7倍。玻璃坠落后,因脱离主体结构的程度不同,部分楼层会出现层间位移角突增的情况。
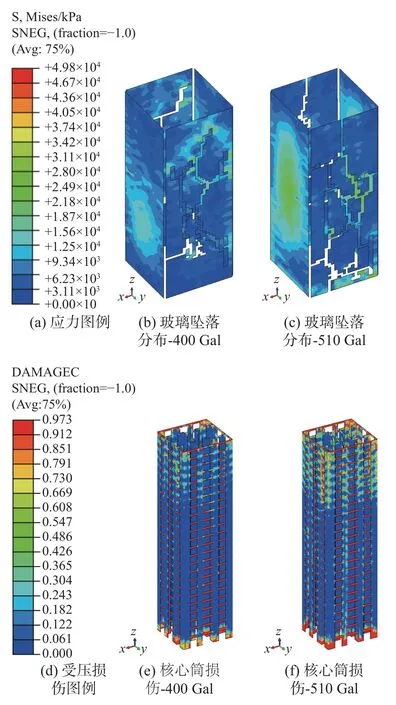
图11 人工波作用下计算结果Fig. 11 Results under the action of artificial wave

图13 人工波作用下结构层间位移角Fig. 13 Story drifts of structure under the artificial wave
为观察各部分层间位移角的变化情况,图14给出两个楼层在不同地震强度作用下的时程曲线。
图14(a)~图14(b)的对比表明:玻璃坠落前,主体结构的层间变形与总体变形相当,即大于玻璃幕墙的;玻璃坠落后,主体结构的变形曲线受玻璃幕墙的影响较小,发展较为平稳。图14(b)~图14(c)的对比表明:在设防烈度大震作用下,主体结构变形小于规范限值1/100,未倒塌,曲线在0轴附近往复波动;当地震强度增至超烈度大震时,主体结构的层间位移角突增至1/35,且偏离0轴发展,表明主体结构呈倒塌状态。

图14 人工波下层间位移角时程曲线Fig. 14 Time history of story drift under artificial wave
3.3 风压作用下计算结果
为研究在风载作用下玻璃幕墙的性能变化,基于风洞试验(1∶440缩尺模型)[21]获得了全楼4896块玻璃单元、持续时间约为600 s的风压时程数据,进行风压作用下的非线性时程分析。
因本结构高度仅为98 m,结合表2的设计结果可以看出,风荷载不控制,在10年、50年重现期风压作用下,玻璃幕墙反应不明显。因此本节主要进行100年重现期风压0.75 kPa、及放大1.1倍后风压为0.825 kPa的时程分析。
图15给出结构上部高度位置,位于不同侧面的四个玻璃单元的风压时程曲线,可见迎风的正面风压值基本为正,侧面及负面为吸风、风压值为负。
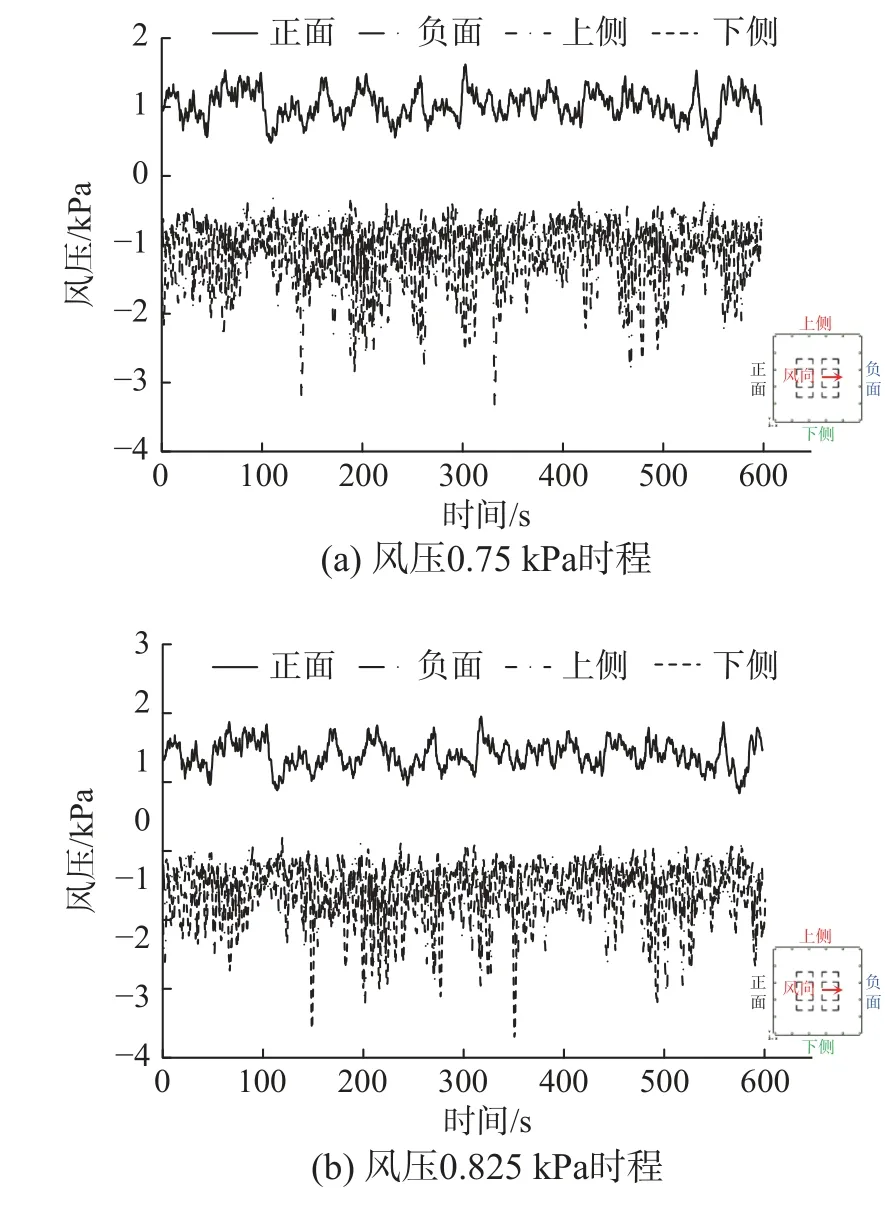
图15 风压时程曲线(四个玻璃单元)Fig. 15 Wind pressure time history (four glasses)
计算基本风压0.75 kPa、0.825 kPa得到的风速分别为34.6 m/s、36.3 m/s(《建筑结构荷载规范》(GB 50009−2012)[22]公式E.2.4-1),对应12级风[23](13级台风)、12级风(14级强台风[24−25])。
表6给出不同风压作用下主体结构的计算结果,可见结构基底剪力和变形随风压增大呈线性增长,与图16中核心筒未出现损伤的结果一致。

图16 风压作用下核心筒受压损伤Fig. 16 Frame-core wall damage under wind pressure

表6 风压作用下主体结构整体指标计算结果Table 6 Main structure index results under wind pressure
图17给出玻璃幕墙的破坏情况,可见,随风压从0.75 kPa增至0.825 kPa,玻璃幕墙未发生破坏,仅侧吸风、正吸风面玻璃应力接近标准值的单元数由1个增至4个。
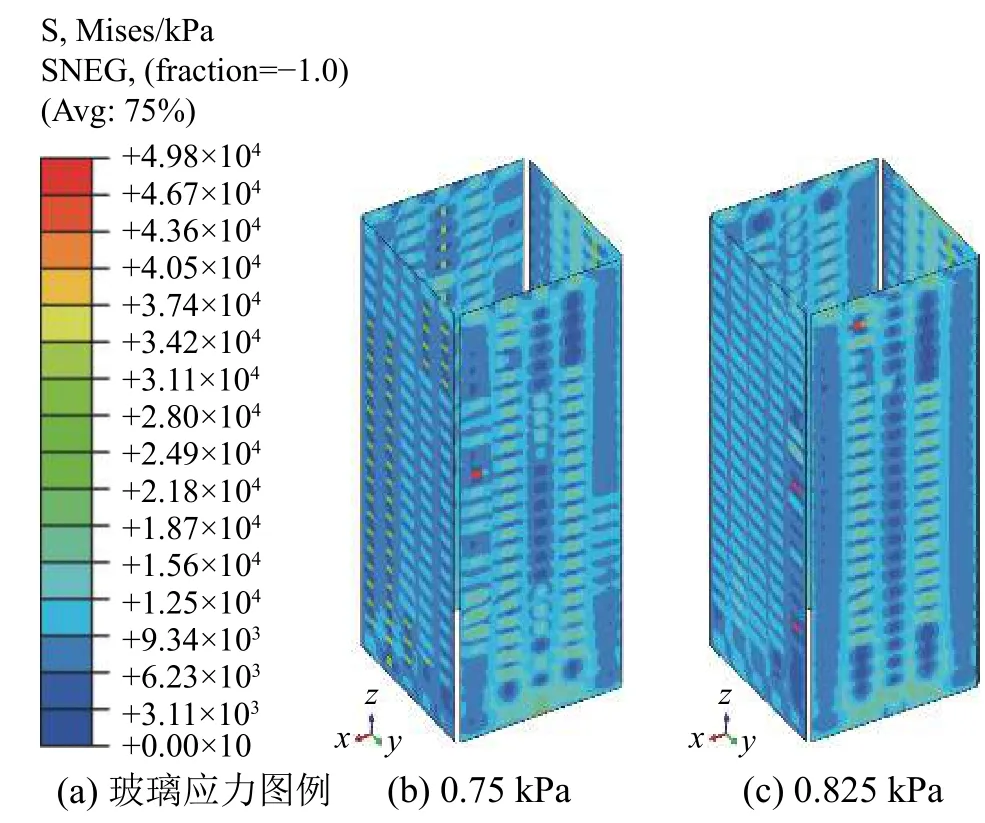
图17 风压作用下玻璃幕墙计算结果Fig. 17 Glass curtain results under wind pressure
图18给出根据式(1)~式(6)计算得到的层间位移角分布曲线,可见与地震作用结果相似,玻璃幕墙未发生破坏时主体结构的层间变形远大于玻璃幕墙自身,对应F12层~F14层主体结构层间位移角为玻璃的4.1倍~5.2倍;玻璃幕墙层间变形占总体变形的比例较小,其中F12层~F14层为19%~23%。增大,地震作用结束后结构响应随风载作用小幅波动,并趋于稳定。

图18 风压作用下层间位移角分布(0.825 kPa)Fig. 18 Story drifts under wind pressure (0.825 kPa)
图19(c)~图19(d)对比表明:地震单独作用下,四个外框角柱(图1中C1~C4)的层间位移角分布曲线基本一致,表明结构共同受力、整体变形;
3.4 风震联合作用下计算结果
为深入研究主体结构和玻璃幕墙在风震联合作用下的性能,本节根据3.2节、3.3节风震单独作用的计算结果做进一步分析。因地震波作用时间短,而风荷载作用的时间则较长,因此进行总时长为60 s的风震联合作用分析,可满足结构(基本周期2.35 s)的计算需求。在整个风荷载作用过程中,地震波在第20 s~50 s进行联合作用,对应的荷载强度为设防烈度大震(400 Gal)和1.1倍100年重现期风压(0.825 kPa)。
主体结构的对比结果由表7、图19给出。可见,表7中C与W+E项不等效,表明结构进入非线性状态后,风震联合作用下的结构响应并非两种荷载单独作用的直接叠加。在联合作用下,结构基底剪力低于风震作用的简单叠加、高于地震单独作用;顶点位移和层间位移角增长较大,为风震简单叠加的121%、106%,为地震单独作用的130%、114%。

表7 风震联合作用下主体结构整体指标计算结果Table 7 Main structure index results under the combined action of wind and earthquake
图19(a)~图19(b)表明:在地震单独作用下结构基底剪力和顶点位移的时程曲线在0基线附近往复振荡,当地震作用结束时趋于0;当考虑风震联合作用时,在初始风压作用下时程曲线略微偏离0轴、作小幅振动,联合地震作用后结构响应当风震联合作用时,四条曲线出现明显差异,比值由1.0增至1.3,表明结构出现了非常不利的扭转效应,需要采取措施进行加强。
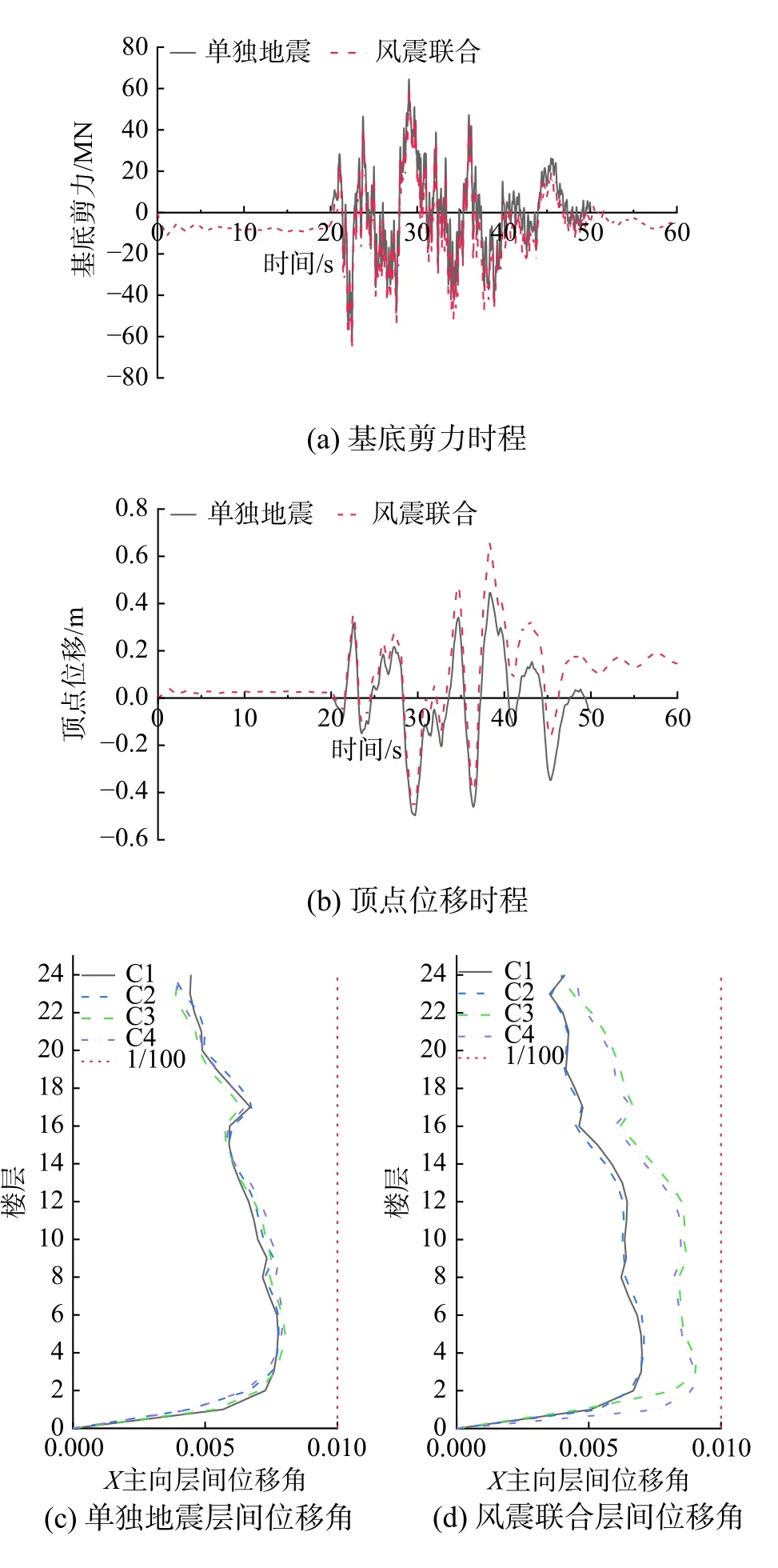

图19 风震联合作用下主体结构计算结果Fig. 19 Structure results under the combined action of wind and earthquake
图19(f)~图19(g)表明:与单独地震作用相比,风震联合作用下底部剪力墙的损伤加重。
图20给出玻璃幕墙的破坏对比结果,可见风震联合作用下玻璃幕墙的破坏范围增大,由单独地震作用的中部楼层分别向上、向下延伸至全部楼层。因地震荷载控制,玻璃破坏范围集中于平行地震作用主向的侧面。

图20 风震联合作用下玻璃幕墙计算结果对比Fig. 20 Glass curtain results under the combined action of wind and earthquake
图21给出总体、主体结构和玻璃幕墙的层间位移角的分布曲线。可见,在玻璃幕墙未坠落的楼层,玻璃自身的层间变形小于主体结构,主体结构变形起控制作用,为玻璃幕墙自身变形的1.3倍;对应玻璃单元发生破坏的楼层,玻璃脱离主体结构进行变形,与图14的结果相似。

图21 风震联合作用下结构层间位移角曲线Fig. 21 Time history of story drift under the combined action of wind and earthquake
本节分析表明:风震联合作用会增大主体结构的非线性响应和玻璃幕墙的破坏范围,使主体结构的变形呈非线性增长、扭转效应增大、平行地震作用主向的玻璃单元破坏范围增大。
4 结论
本文以98 m高的框筒结构为例,采用动力弹塑性分析方法,研究风、地震单独及联合作用下,主体结构和玻璃幕墙的性能变化,主要结论如下:
(1)实现了同时考虑主体结构与玻璃幕墙结构的总体有限元分析模型构建,通过分析得到玻璃幕墙作为围护结构对主体结构影响不大。在风、地震单独和联合作用下,通过总体、主体结构和玻璃幕墙三部分的层间位移角分解得到,主体结构的层间变形大于玻璃幕墙自身的,在结构中部楼层为玻璃幕墙层间变形的3.0倍~5.2倍。
(2)在设防烈度和超烈度大震作用下,随地震强度增大,主体结构的非线性响应和玻璃幕墙的坠落范围增大,其中基底剪力的增长小于顶点位移和最大层间位移角的。风荷载对普通高层建筑结构的影响较小,在100年重现期及放大1.1倍风压作用下,结构处于弹性状态,基底剪力、顶点位移和最大层间位移角呈线性变化,玻璃幕墙未发生坠落破坏。
(3)风震联合作用下,主体结构出现不利的扭转效应,并且主体结构和玻璃幕墙的非线性响应,大于风震单独作用的直接求和。如设防大震与1.1倍100年重现期风压联合作用时,主体结构的顶点位移和最大层间位移角为风震单独作用求和后的121%、106%,外框角柱的层间位移角之比由1.0增至1.3;玻璃幕墙的坠落面积大于风震单独作用的叠加。
(4)在地震单独和风震联合作用下,平行受力主向的玻璃幕墙受力较大,容易发生破坏。

