基于改进萤火虫算法的有限元模型修正
刘 纲,陈 奇,雷振博,熊 军
(1. 山地城镇建设与新技术教育部重点实验室(重庆大学),重庆 400045;2. 重庆大学土木工程学院,重庆 400045;3. 中铁十一局集团第五工程有限公司,重庆 400037)
有限元分析技术具有应用成本低、计算过程直观等显著优点,已广泛应用于各种复杂机械、航空及土木工程结构的设计、性能分析与损伤识别[1−2]。但实际结构的复杂性、边界条件等的不确定性,使得有限元计算结果与实际结构响应往往存在一定差异[3]。为使有限元模型能够更为准确地反映结构实际状态,有限元模型修正技术得到了大力发展,已成为当前重点研究方向和前沿[4]。
目前,有限元模型修正技术多采用参数型修正法,即对有限元模型中的材料特性、截面尺寸等参数进行修正,具有简单直观、物理意义明确等特点[5]。修正步骤主要包括目标函数建立、修正参数确定及优化算法选取等,其中,合理算法的选取是保证修正精度的关键因素[6]。因为传统的牛顿法、一阶优化法等确定性搜索优化算法对初始值较为敏感,且易陷入局部最优[7],故而近年来各类随机搜索优化算法得到了更多的发展及应用。
李成等[8]提出了基于人工鱼群算法的结构模型修正方法,以每层层间刚度为修正参数,完成了实验室3层框架的模型修正;杜大华等[9]提出一种基于模拟退火算法的有限元模型修正方法,并以火箭发动机喷管模型为例实现了7参数的有限元模型修正;苏越[10]提出了基于蚁群优化算法的有限元模型修正方法,并完成了虎门大桥的有限元模型修正;夏志远等[11]提出了基于高斯白噪声扰动的粒子群优化有限元模型修正方法,某在役桥梁结构模型修正结果表明,各阶频率误差降低至8.86%以下。此外,差分进化算法、蜂群算法、遗传算法等[12−16]也被大量应用到结构动力学模型修正中,形成了一系列基于仿生学的有限元模型修正方法,并在土木、机械等结构中显示出良好的修正效果。
萤火虫算法(firefly algorithm,FA)作为一种新兴启发式智能仿生算法,具有参数少、易实现、全局寻优能力强等特点,在状态预测、传感器优化布置、信号降噪处理等领域得到初步应用[17−21]。但标准FA算法存在着后期收敛速度慢、收敛精度低等不足,严重制约了FA在实际工程中的应用。针对这一问题,本文通过对随机吸引度因子及自适应步长因子的改进,提升算法收敛效率与精度。并通过函数、简支梁数值模拟和某实际连续刚构桥的有限元模型修正,验证改进FA算法有效性,从而为有限元模型修正提供优化方法支撑。
1 萤火虫算法及其改进
1.1 萤火虫算法基本原理
萤火虫算法是一种随机搜索算法,其基本思路是借鉴萤火虫的自然行为,将优化问题中的迭代搜索看作是萤火虫相互吸引而自发聚集的过程,从而通过模拟萤火虫群体行为实现最优化问题求解。在自然界中,萤火虫个体的吸引力与发光强度正相关,与它们之间距离的平方负相关;亮度小的萤火虫个体向亮度大的萤火虫靠近,从而完成萤火虫种群的自发式移动和聚集[17],如图1所示。图1中,每个黑色原点为一只萤火虫个体,代表优化问题的一个可能解;萤火虫周围的光晕表示其发光强度,代表该只萤火虫的适应度函数值大小,适应度值越优,萤火虫的发光强度越强、光晕范围越大;两只萤火虫之间的虚线代表吸引力,虚线越粗,代表吸引力越大。

图1 萤火虫发光强度示意图Fig. 1 Luminous intensity of firefly
萤火虫的移动过程就是可能解不断向最优解的迭代过程,下面给出该过程的数学描述。假设Xi=(x1i,x2i,···,xdi)是群体中的第i只萤火虫,其中i =1, 2, 3, ···, N。N与d分别表示种群中萤火虫的个数与修正参数的维度。对任意两只萤火虫Xi与Xj(i≠j),定义两者之间的欧氏距离rij为:
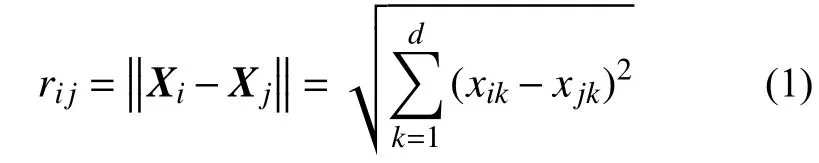
则两者之间的吸引度因子为:

式中:β0为两只萤火虫距离rij=0时的吸引力,一般取为1;γ为光在空气中的衰减系数,一般取为0.01~100。假设萤火虫Xj(j≠i)的适应度值优于Xi,则萤火虫Xi会被萤火虫Xj吸引而更新,有:
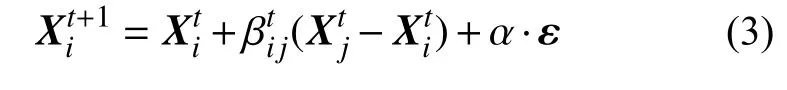
式中:j=1, 2,···, i−1, i+1,···, N,上标t为当前迭代步数;α为步长因子,取值范围为0~1;ε为d维随机向量,服从正态分布N(0,1)。若Xi为当前最佳,则对Xi进行随机移动:

萤火虫Xi在第t步的具体更新过程如图2所示。

图2 第i只萤火虫更新步骤Fig. 2 Updating steps of the ith firefly
1.2 萤火虫算法改进
在式(3)中,萤火虫Xi的更新过程可细分为跳跃操作dxβ和随机游走操作dxα:

因此,该算法的优化性能主要取决于吸引度因子βij和步长因子α,若这两者设置不当,会导致算法精度下降甚至难以收敛。针对这一问题,本文提出改进自适应参数控制算法,以提升计算效率及精度。
1) 随机吸引度因子
吸引度因子βij在不同γ取值下随着欧氏距离rij的变化规律如图3所示。
由图3知,γ较大时,吸引度因子βij及跳跃距离dxβ均会随着距离增加快速趋近于0,致使搜索停滞;γ较小时,βij往往过早趋近于1,此时,跳跃操作可近似等效为:

图3 βij迭代过程Fig. 3 The iterative process of βij
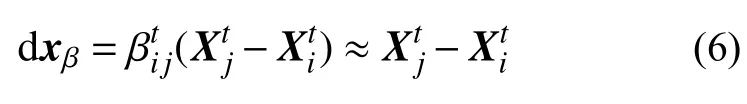
此时,亮度较低的萤火中直接跳转到高亮度的萤火虫附近,难以对状态空间内其他位置进行探索、产生有效跳跃,导致发现率低、易陷入局部最优。因此,衰减系数γ大小决定了萤火虫的可视范围,在原萤火虫算法中,衰减系数γ为定值,不会随着迭代过程而改变,故无论γ取值如何,不可能同时兼顾迭代初期大范围快速搜索、迭代后期小范围精细搜索的需求。
针对这一现象,本文取γ=0.01,使各萤火虫的βij大于0.8,拥有较大的初始搜索空间,避免计算停滞;同时,引入隔代随机吸引度因子,如式(7)所示,使βij有机会取较小值,解决因γ取值过小导致βij过早趋于1而致使解的同质化现象,以提升算法遍历性。

式中:rand表示从均匀分布U(0,1)中抽取随机数;mod(t,2)=0表示迭代步数t为偶数。通过设置隔代随机吸引度因子改善算法搜索空间。以某二维函数优化过程为例,跳跃操作改进前后搜索变化如图4所示。由图4可知,改进前由于βij过早趋近于1,跳跃距离dxβ沿固定线性路径分布,搜索范围单一。而改进吸引度因子有效增加算法搜索范围,扩大了算法的搜索路径,提升了算法遍历性,提高了计算精度。

图4 跳跃操作产生的距离dxβFig. 4 The distance dxβ produced by jump operation
2) 自适应步长因子
在萤火虫算法迭代初期,随机选取的初始值往往离真值较远,则此时步长因子α应取较大值以保证获得较广的探索空间,而随着算法不断迭代优化,种群中所有个体将逐渐聚集,最终收敛到真值,即:

此时,α应趋近于0。否则,算法将在最优解附近大幅振荡,影响算法的收敛性能。从以上分析可知,α值应随着迭代演化而逐渐减小,但缩减的速度大小会影响最终计算效率与精度。缩减速度过大,会导致dxα过早趋于0,迭代过早停滞,无法收敛到最优值;缩减速度过小,会导致迭代后期的dxα过大,使结果在最优解附近振荡。因此,本文提出参数α自适应动态更新策略:

式中:α0为步长因子初始值,建议取为1;T为最大迭代步数;c为常数缩减因子,可根据实际情况取值以获取适宜的步长因子自适应缩减速度。根据算例实际计算结果分析,建议自适应步长因子α的缩减系数c取为15,此时,α及dxα变化规律如图5所示。

图5 α及随机游走距离dxα变化曲线Fig. 5 Curves of α and random walk distance dxα
改进后的萤火虫算法如图6所示,其中,虚线框内内容为算法改进部分。

图6 算法流程图Fig. 6 Algorithm flow chart
2 算法性能测试
2.1 试验设置

采用3个常用的基准测试函数检验改进FA算法的效果(如图7所示),算式如下:式中:d 为参数的维数,所有函数均取为2; f1为单峰函数,用于考察算法的收敛速度; f2虽是单峰函数,但其全局最优点隐藏于一条狭长的通道中不易获得; f3是典型的非线性多模态函数,具有大量局部极值,可有效检验算法的全局搜索性能。f1和 f2的参数取值范围为(−10, 10),f3的参数取值范围为(−32.768, 32.768),各函数图像如图7所示。改进及标准FA算法的萤火虫总数均取为60,最大迭代步数取为1500。
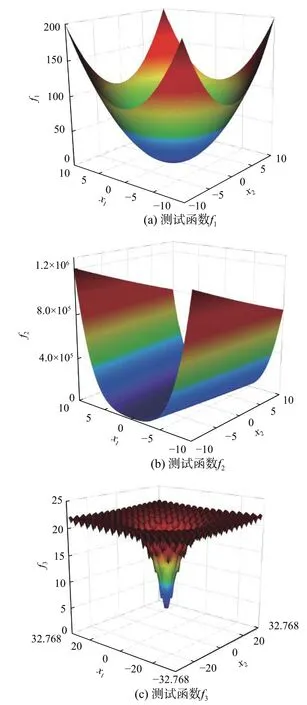
图7 各测试函数3维图Fig. 7 Graphical model of each test function
2.2 试验结果
因萤火虫算法是一种随机算法,为确定统计意义上的优化效果,式(10)中每个函数分别优化20次,统计最终计算结果及计算精度达到0.01[11]所需平均迭代步数。计算结果如表1所示。限于篇幅,图8仅给出f1与f3函数20次平均优化迭代过程函数值与迭代步数的关系。

表1 测试函数计算结果Table 1 Computed results of test functions

图8 f1、f3函数20次平均优化迭代过程Fig. 8 The 20 average iterative processes of f1、f3
由表1知,对于所有基准测试函数,改进FA算法在优化平均值方面均有较明显提升,且从标准差来看,改进FA算法具有更强的算法稳定性;由图8知,在优化计算过程中,标准与改进FA算法在计算初期收敛速率相当,但迭代50次左右以后,由于参数没有适应性功能,标准FA的优化速率急剧降低,陷入局部最优解,在多峰函数计算时,未能收敛。而改进FA算法,无论处理单峰函数还是复杂多峰函数,在900步前均能保持较好的收敛趋势,有效提升了算法中、后期收敛速度,且计算精度远超设定阈值,拥有较高的收敛精度。
3 基于改进FA的有限元模型修正
3.1 基于改进FA算法的有限元模型修正方法
有限元模型修正的3个主要步骤是:确定目标函数、修正参数及修正算法。目标函数往往根据可获得的实测数据确定。在土木工程中,结构动态测试在随机激励下容易实现,故选取识别的固有频率与模态振型,建立如下目标函数:

式中:n、m分别表示频率ω与振型φ的阶数;下标e、r分别表示有限元模型计算值与实测值;CV表示测量变异系数。通过变异系数加权,给予测量误差较小的项以较大的权重,减小测量误差对修正结果的影响。
其次,选取弹性模量、密度、几何尺寸等作为修正参数[5],并用向量X=[x1,x2,···,xd]表示。
最后,使用改进FA算法进行有限元模型修正。通过抽样形成初始萤火虫种群,每个萤火虫代表一个参数向量X,将参数向量代入有限元模型计算结构响应,进而通过式(11)确定每个萤火虫的适应度值,再按照图5中的流程更新萤火虫位置,直到达到迭代终止条件。
3.2 简支梁模型修正
对一跨度为10 m的简支梁进行模型修正。该梁高H=0.6 m,宽B=0.4 m,材料密度为2500 kg/m3,沿长度方向将梁均分为10个单元,记为编号1~10,并设置9个振型测点,记为编号①~⑨,如图9所示。

图9 简支梁模型Fig. 9 The model of the simple-supported beam
选取10个单元的弹性模量为修正参数Ei(i=1,2, ···, 10)。为方便修正,对修正参数值进行归一化无量纲处理,即θi=Ei/E0,其中,E0=3.3×104MPa,则修正参数为无量纲量θi。考虑环境、施工工艺等因素影响,假设混凝土实际弹性模量存在一定离散性,随机设置各单元的弹性模量“真值”,如表2所示。

表2 各单元弹性模量真值Table 2 The actual elastic modulus of each element
在实际问题中,由于测量误差,每次测量结果往往不尽相同,故一般使用多次测量结果以减少误差影响。为模拟这一过程,首先将预设真值代入有限元模型计算获取前6阶频率和前3阶竖向振型;然后对各阶频率及振型分别添加1%噪声以模拟测量误差,最终“实测”频率信息如表3所示。

表3 实测频率信息Table 3 The information of measured frequency
基于上述“实测”值,分别使用原始FA及改进FA对简支梁进行有限元模型修正。修正时,各萤火虫参数初始值从均匀分布U(0, 2)中随机抽取,种群中萤火虫个数N=20,每只萤火虫包含变量维数d=10,最大迭代步T=3000。本文仅列出某只萤火虫迭代收敛情况,如图10所示。参数修正结果如图11所示。

图10 某只萤火虫各维参数收敛情况Fig. 10 Convergence of parameters of one firefly

图11 修正前、后参数及误差对比Fig. 11 Comparisons of parameters and errors before and after updating
从图10可看出,标准FA算法由于参数不可适应性,迭代过程易陷入停滞,修正效率低,且最终计算结果未能全部收敛到真值;所提改进算法在1000步左右即可收敛,且均能收敛到真值。从图11可知,修正前各参数误差均大于9%,其中单元4的弹性模量误差最大,高达66.7%;标准FA修正后模型的个别参数计算误差不减反增,修正效果较差;改进算法修正后模型各参数误差均降低至1.08%以下,其中单元1参数误差仅为0.08%。故所提改进算法极大地提升了原始算法的计算性能,具有良好的修正效果。
3.3 某连续刚构桥修正
某三跨预应力混凝土连续刚构桥跨径组合为140 m+240 m+140 m,根部梁高为15 m,跨中及边跨直线段梁高均为4.5 m,主梁采用单箱双室截面,箱梁腹板采用直腹板,主梁材料采用C50混凝土;桥墩主墩采用双薄壁墩,墩身薄壁截面尺寸为16 m×25 m,两薄壁间净距为7 m,墩高为55 m,墩身材料采用C40混凝土。C40、C50混凝土初始弹性模量分别取为3.25×104MPa、3.45×104MPa,初始密度均取为2600 kg/m3。
利用商业有限元软件建立该桥模型,所有构件均采用欧拉三维梁单元模拟。在桥墩底端,桩基础与承台基础具有很大的刚度且与基岩嵌固良好,故将其视作固端约束;主梁与墩顶采用固接;桥梁两端为活动支座,在有限元中各设一个单向支座,提供X、Z(垂直纸面)方向的平移约束与绕Z方向的转动约束。初始有限元模型如图12(a)所示,模型共包含547个节点,272个单元。
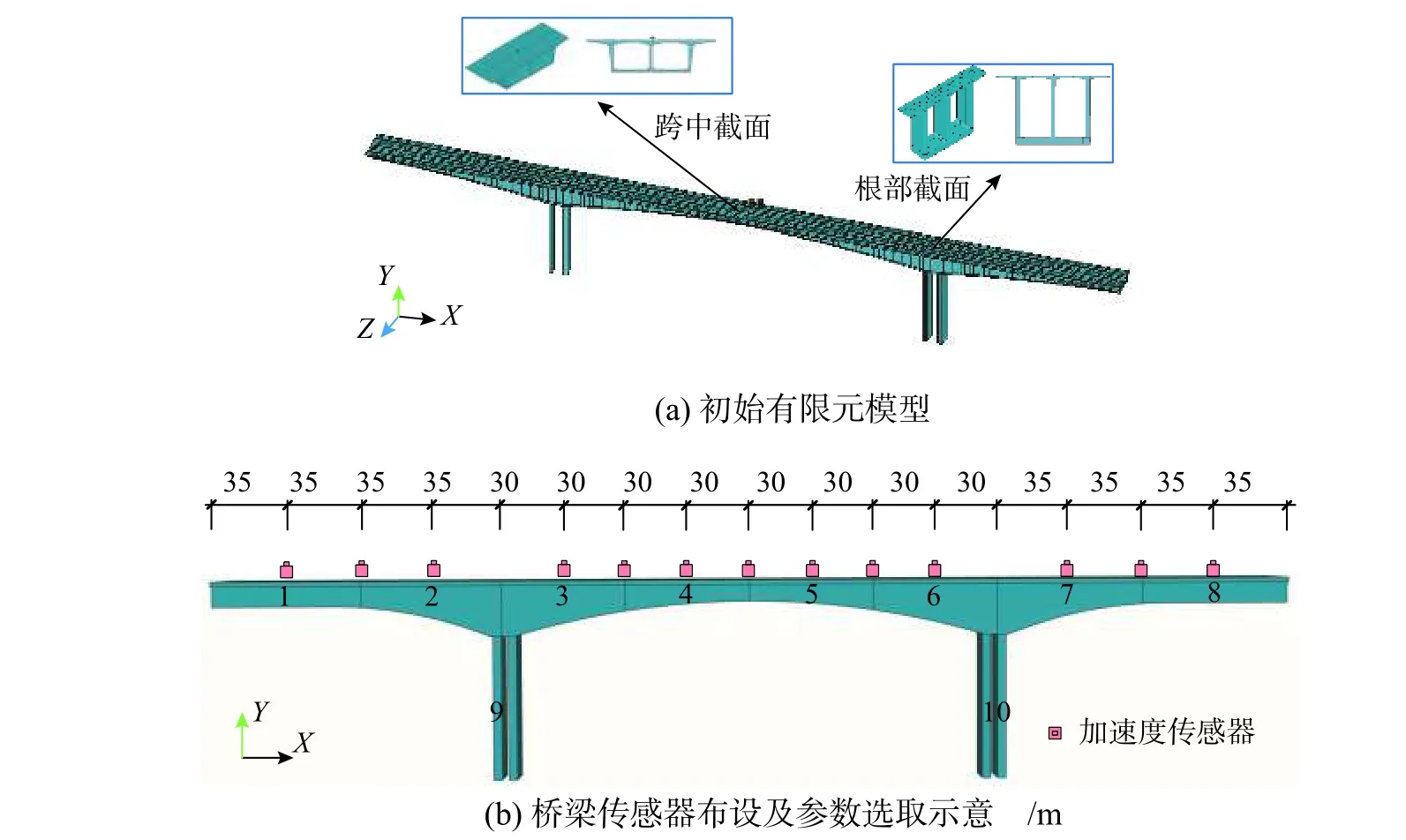
图12 初始有限元模型、传感器布设及参数选取示意图Fig. 12 The initial finite element, the sensor arrangement and the selection of the parameters
传感器布设位置如图12(b)所示,共采用13个加速度传感器进行实桥环境随机激励测试,采样频率设为25 Hz,分别进行5次采样以减少随机误差的影响,每次采样时间持续30 min。通过频域分解法(frequency domain decomposition)处理测试数据获得的前4阶竖向自振频率、竖向振型与初始模型计算结果对比如表4所示,除第4阶频率误差较小之外,其余阶频率误差均达到6%以上。

表4 模型修正前后计算结果对比Table 4 Comparisons of the calculation results before and after model updating
该桥主梁施工采用悬臂浇筑工艺,考虑到相邻节段梁施工间隔较近、差异较小,为减少计算参数,将相邻节段梁的弹性模量、密度分别视为一个参数,参数选取如图12所示,其中1~10为选取的合并后节段编号,故全桥共选取20个修正参数。修正时,萤火虫个数N=20,最大迭代步数T=2000。
由表4知,改进FA算法修正后有限元模型的各阶频率误差均明显下降,均低于3.25%,修正效果较好;而原始FA算法修正后模型的第3阶、4阶频率误差反而略微增大,最大误差出现在第3阶,达到7.34%,修正效果较差;根据表中MAC数值及图13(限于篇幅,只列出前2阶振型)可知,两种算法修正后各阶振型与实测振型吻合度均有提升,但总体上改进FA计算精度优于原始FA。
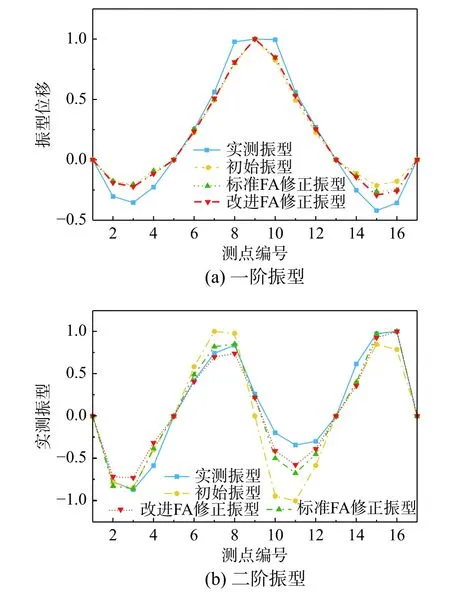
图13 振型对比图Fig. 13 Comparisons of mode shapes
综上所述,改进FA算法相较于原始FA算法在实桥有限元模型修正中表现出更加良好的修正效果。
4 结论
针对标准FA算法缺陷,提出了参数自适应改进方法,通过多种单、多峰函数以及简支梁数值算例与某大桥有限元模型修正,验证了所提方法的有效性。所得结论如下:
(1) 根据FA算法更新原理,分析吸引度因子βij与步长因子α的变化规律,提出参数自适应方法,并通过4个具有不同形式特点的单、多峰测试函数验证了改进FA算法相较于原始FA算法在寻优速率、精度方面的优越性。
(2) 分别将改进前后的FA算法应用于10维简支梁模型修正,结果表明,原始算法在修正中易陷入停滞,修正精度较低,而改进算法拥有较好的修正效果。修正前后,简支梁参数最大误差由初始模型的66.7%降低至修正后的1.08%,且修正后最小误差降低至0.08%。验证了改进FA算法在结构有限元模型修正中的应用可行性。
(3) 基于环境随机激励测试与频域分解法,识别某连续刚构桥的竖向前4阶频率、振型。结果表明,修正前频率最大误差为14.47%,改进算法修正后各阶频率相对误差明显下降,均控制在3.25%以内。此外,修正后的各阶振型与实测振型吻合度均有提升,表明所提方法拥有良好的修正效果。

