基于改进粒子群算法的避障轨迹规划*
马东阳 库祥臣 米 显 杨星涛 赵欢乐
(河南科技大学机电工程学院,河南 洛阳 471003)
机器人的关节运动结果直接影响着作业效果,对关节轨迹规划的研究可提高机器人工作效率,减少运动过程中的抖动和冲击,对于延长机器人使用寿命,提高效益具有重要意义[1−3]。目前轨迹规划优化方法有很多,可通过改进规划算法,使用高阶多项式曲线[4]、B样条曲线等以提高轨迹的平滑性,使机器人关节运动更加平稳[5];针对轨迹参数以时间最优、冲击最优和能量最优等为目标应用算法寻优[6−7]。浦玉学[8]等针对机器人轨迹能耗优化问题改进引力搜索算法,提升算法搜索能力,完成低能耗运动轨迹规划。王超[9]等提出一种自适应的遗传算法避免陷入局部极值,以时间最短为目标,完成平滑轨迹规划。李俊[10]等通过动态改进遗传算法参数改善局部最优问题,结合样条函数生成机器人平稳运动轨迹。基于以上研究理论可知算法的收敛速度和全局搜索能力,避免陷入局部极值,是算法使用的依据,对轨迹最优规划有重要影响。
本文以机器人避开障碍物,关节转角增量最小和用时最短为目标,使用多项式函数完成轨迹描述。提出指数曲线递减和动态调整策略的改进粒子群算法,通过多项式参数寻优,完成轨迹优化,并进行实验和仿真验证。
1 避障轨迹规划
通过参数寻优的方法完成避障轨迹规划总体流程如图1所示。

图1 规划方法流程
1.1 机器人避障任务描述
机器人分拣任务如图2所示,由机器人完成传送带上位置a处零件的抓取,然后根据测量装置b处的信息将零件分拣至不同的物料盒c中,路径点a记为起点,路径点b记为测量作业点,路径点c记为目标点。

图2 任务描述
在测量操作过程中为避免机器人本体与测量装置及其他装置的碰撞,传统上是由工程师根据经验,采用拖拽示教的方法,确定运动轨迹。本文研究以机器人各关节转角增量最小,运动时间最短为优化目标,在任务空间中,障碍物信息已知,通过参数寻优完成避障轨迹规划,进而提高作业效率。
1.2 碰撞检测模型建立
如图3所示,基于包围球理论[11],根据机器人本体特征将其简化为4个圆柱体C的组合,并将障碍物六面体B简化为球体A。

图3 包络圆柱理论模型
图3中球体A中心和六面体B的中心一致,六面体B的最大外围尺寸即为球体A的直径2RA,圆柱体C的半径记为RC。进一步简化模型,将4个圆柱体C看作4条线段l,其外径做如下处理:R=RA+RC,R称为包络半径。空间中线段与点的距离决定两者的位置关系,据此建立碰撞检测模型。为确定空间中线段的位置,根据机器人关节变化矩阵求得关,关节5的位节2的位,关节3的位,关节4的位,关节6的位,则3个线段模型在三维空间的表达式如式(1)所示。

式中:di为线段i到球心的距离,i=1,2,3。若di>R,则线段与球不接触无碰撞,否则接触即发生碰撞。
1.3 运动轨迹的数学描述
本文在关节空间采用多项式函数进行轨迹规划,通过寻找一个最优作业点,连接前后两段轨迹,作业点关节信息与多项式参数相关,通过改变参数来改变作业点信息完成避障。作业点和起点之间与该作业点和目标点之间的轨迹使用五次多项式描述。对于单关节在路径点n之后的轨迹曲线数学描述如式(3)所示。

路径点n和n+1处的关节角度,角速度和角加速度分别表示为θn、,关节从路径点n经过时间tn到达路径点n+1,则θn(t)的6个约束条件如式(4)所示。
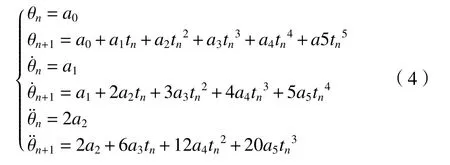
求解θn(t)可得各系数,经过整理,该段轨迹函数如式(5)所示。

根据式(5)可知只要输入θn、θn+1、和tn即可求出该段的轨迹函数θn(t)。分别计算起点到作业点和作业点到目标点的两段轨迹函数θ1(t),θ2(t)根据已知条件:起点的机器人各关节角度θ0=[q01,q02,q03,q04,q05,q06],终点的各关节角度θf=[qf1,qf2,qf3,qf4,,qf5,qf6],起点和终点的各关节角速度,角加速度,在测量作业点处,则需要确定的参数分别是作业点处各关节的角度θz=[qz1,qz2,qz3,qz4,qz5,qz6]和两段轨迹时间t1、t2。
2 参数寻优模型
2.1 优化模型建立
本文以各关节角度增量最小和关节运动的时间最短为优化目标建立目标函数如式(6)所示。

运动学约束如式(7)所示。

式中:θjmax、分别表示关节j的最大转角、速度和加速度值。fθ是各关节角度增量之和,计算方法如式(8)所示。
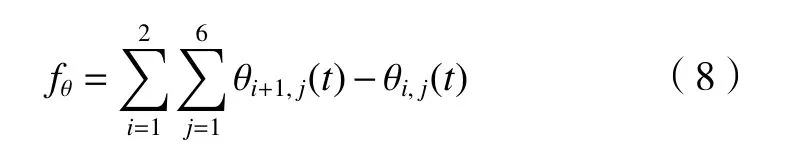
ft是各段运动时间之和,ft=t1+t2。η1、η2是转角增量权重和时间权重。在优先保证时间优先的情况下,设置η1<η2。
在目标函数中还需加上机器人本体与障碍物不发生碰撞的约束条件,本文使用惩罚函数处理碰撞约束,构造新的目标函数如式(9)所示。

式中:µ为罚因数;fob为碰撞检测项,将轨迹函数插入n个采样点,在每个采样点处分别计算距离d并进行碰撞判断,将结果记为fobi规定不碰撞为1,反之为0。将采样点处的计算结果累乘如式(10)所示。

根据以上分析,参数寻优的避障轨迹规划问题即在满足碰撞检测条件下关节转角增量最小,时间最短的多项式结构参数p=(θzj,t1,t2),j=1,2,···,6的寻优问题。
2.2 改进粒子群算法
粒子群优化算法(particle swarm optimization,PSO)算法结构简单,通过追随当下最优解来搜寻全局最优[12]。标准PSO算法由于参数固定,在迭代求解过程中若粒子个体认知权重大于群体社会性权重,则可能使算法后期无法收敛,反之则可能出现收敛速度快陷入局部极值无法寻到全局最优,本文通过改进PSO来优化这一情况。
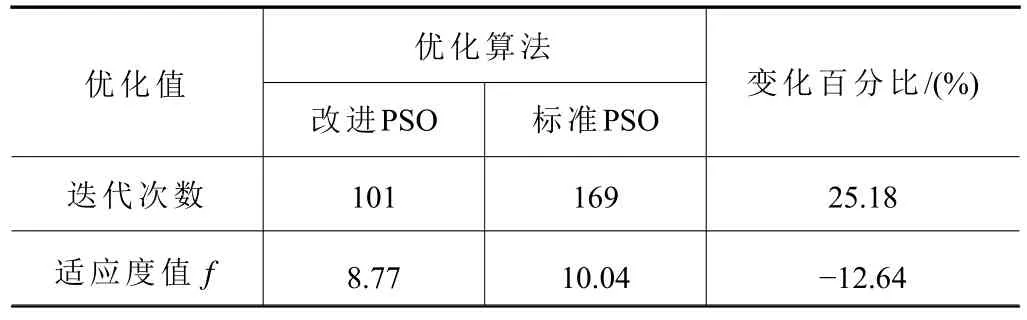
粒子更新公式如式(11)所示。
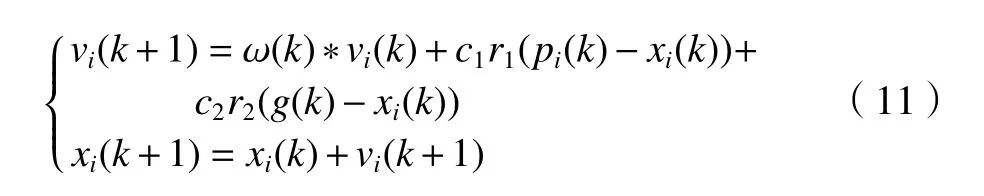
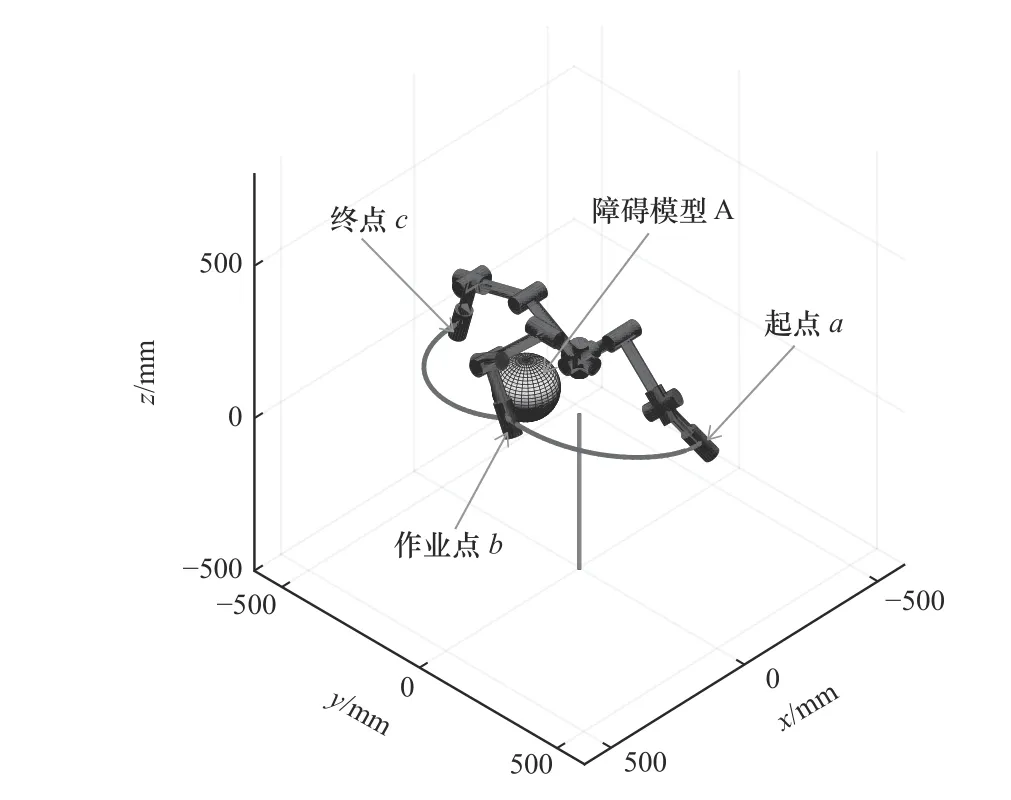
其中:pi(k)是个体粒子i的适应度最优值,g(k)是粒子种群的适应度最优值,r1、r2是[0,1]内的随机值。速度更新式(11)当中:ω(k)∗vi(k)是粒子自身惯性值,ω值越大算法早期全局搜索能力越强,后期较小的 ω可加快算法收敛速度;c1r1(pi(k)−xi(k))是粒子的个体认知能力,表示粒子有逼近自身记忆中最优值的趋势;c2r2(g(k)−xi(k))是粒子趋近整个种群或者邻域内最优值的趋势。c1、c2是加速权值,算法早期应使c1>c2,粒子个体认知能力的意义要大于群体决策,后期为快速收敛于全局最优则应使c1 本文将通过改进粒子群参数 ω和c1、c2来改进PSO算法。其中根据式(12)给予惯性权值指数曲线递减策略,给与加速常数正弦函数动态调整。 式中:ωmin为初期惯性权值;ωmax为最大惯性权值;r3是在[0,1]之间的随机数;k为当下迭代次数;kmax最大迭代次数。 根据上述目标函数模型中作业点处各关节的角度和两段轨迹的时间值构成种群中每个粒子,其编码方式为:pi=(θzj,t1,t2),j=1,2,···,6。初始化加速权值c1为0.8,c2为0.6,惯性权值为1,粒子的初始速度和初始位置为0,终止条件是迭代次数达到设置代数,同时满足碰撞检测约束条件,改进PSO算法的流程如图4所示。 图4 改进PSO 算法流程 以JakaMinCobot机器人为研究对象,采用改进的DH建模方法,建立连杆坐标系如图5所示。 图5 连杆坐标系 根据连杆坐标系得到机器人各关节的改进的DH参数如表1所示。 表1 改进DH参数 其中各关节的约束如表2所示。 表2 关节运动学约束 正运动学变换矩阵推导如式(13)所示。 将DH参数代入式(13)即可得到机器人各关节相对基坐标系的齐次变换矩阵。 设机器人各关节初始角度q0=[0,0,90°,0,90°,0],根据运动学公式计算可得关节6的坐标变换矩阵: 同时使用Matlab中的Robotic构建机器人模型使用Fkine函数计算结果与相同,如图6所示机器人在此位置姿态与机器人实物对比一致,验证运动学模型建立准确。 图6 运动学模型验证 同时运用MonteCarlo法模拟机器人工作空间如图7所示,其中机器人末端在x轴的移动范围在(−600,600),在y轴的移动范围在(−500,500),在z轴的移动范围在(−500,800),由此设置机器人起点a坐标为(−75,366,60)、终点c坐标为(6,−426,84)以及障碍球心坐标为(250,0,200),其中包络半径设为R=90 mm。并通过机器人自带求逆解函数kine_inverse解出路径点a、c处相应的关节角度,a=[−1.571,0.785,1.571,1.047,0.524,0.785],c=[−4.712,1.047,0.785,0,1.047,−1.047]。 图7 工作空间模拟 设置罚因数µ=10,算法种群个数为30,权重因子η1=0.6,η2=0.8,最大迭代次数200。如图8所示在经过迭代100次之后,算法收敛,得出轨迹函数待求参数值p=[−3.141,0.698,0.785,0.523,1.571,1.463,5.58,3.36],优化结果对比如表3所示,与标准的粒子群算法相比改进算法收敛速度提高25.18%,目标函数值减少12.64%达到全局最优。 表3 优化结果对比 图8 算法迭代结果 将优化参数代入式(5)即可求出两段运动轨迹函数,同时运用Matlab仿真可得到机器人在笛卡尔空间的避障运动轨迹如图9所示。 图9 避障轨迹 如图10所示,利用运动学模型求得l1、l2、l3在运动过程中到障碍物中心的距离d变化曲线,距离的最小值为107.8 mm均大于障碍物模型的包络半径90 mm,满足避障约束条件。 图10 避障距离变化 利用Matlab对五次,三次多项式仿真对比。以关节1~3为例绘制角位移,角速度和角加速度的仿真曲线如图11所示,五次多项式可将起点、终点和作业点处角加速度设为零,且加速度变化更加平滑,可减轻机器人的振动和冲击,使作业过程更加平稳,三次多项式在路径点处加速度有突变,五次多项式则可更好地满足应用要求。 图11 轨迹规划仿真对比 对于机器人提供的动态库函数和API接口,利用C++编程二次开发,将上述优化的得到的避障各路径点参数代入机器人运动控制函数,并采集机器人实时运动原始数据,使用Matlab绘制曲线,图12中可知机器人避障运动轨迹平滑,如图13~15所示关节转角,速度,加速度峰值均在运动学约束范围内。 图12 避障运动轨迹 图13 关节转角 本文研究了任务空间中通过参数寻优的方法完成机器人全局避障轨迹规划得出以下结论: (1)采用五次多项式作为轨迹函数,建立机器人碰撞检测模型,并引入罚函数来处理避障约束条件,结合机器人运动学模型,完成了机器人避障规划,仿真验证了五次多项式由于路径点加速度可控更加满足应用需求,该方法流程可进一步推广至多自由度串联机器人的避障研究当中。 图14 关节速度 图15 关节加速度 (2)运用指数曲线递减和动态调整策略改进粒子群算法,加快粒子群收敛速度,提高算法的全局搜索能力,为机器人在线避障轨迹规划奠定了基础。

3 仿真分析与验证
3.1 运动学模型建立
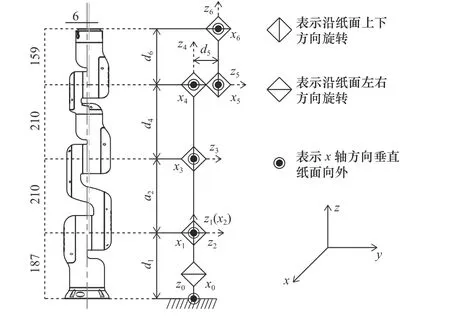



3.2 模型验算与工作空间分析



3.3 优化计算与实验分析





4 结语