基于最大增量速度的RC框架模型易损性分析
佟 瑶,刘本山,郭骅山,段厚瑞,曾庆龙,*
(黑龙江大学 a.建筑工程学院;b.水利电力学院,哈尔滨 150080)
0 引 言
地震是一种常见的自然灾害,具有一定的爆发性和突发性。一场强烈的地震能给一座城市带来毁灭性的打击,如1976年唐山地震、2008年汶川地震等。世界上最早对地震的研究起源于19世纪80年代[1],但由于地震的不确定性,预测地震仍是世界难题之一。对建筑结构的震害损失预测和对既有建筑的加固及其抗震性能研究已成为了当今研究的热点。而地震易损性恰好是解决这两类问题的基础,也是当前地震工程的重点研究内容[2]。基于结构地震易损性分析,可以得到结构抗震性能和地震风险评估[3- 4],其结果的精度对损失评估有直接影响[5]。
1 RC框架结构模型的建立
以防灾科技学院新建北校区教学楼为研究对象,该教学楼位于河北省三河市燕郊开发区,结构形式为RC框架,所处场地类别为Ⅲ类,地震烈度为8度(0.2g),设计地震分组为第一组,抗震等级为二级。该楼共8层,跨数为7×3,外形尺寸为46.2 m×18.4 m,1~2层层高为4.5 m,3~8层层高为4.2 m;1~4 层柱截面为0.8 m×0.8 m,5~8层柱截面为0.6 m×0.6 m;KL1截面尺寸为0.3 m×0.75 m,KL2截面尺寸为0.5 m×0.5 m,L-1截面尺寸为0.25 m×0.6 m,结构平面布置见图1。混凝土强度1层柱为C50,2~3层柱为C45,4层柱及以上为C30,梁板均为C30。荷载信息参照《建筑结构荷载规范》(GB50009-2012)[6],1~7层恒荷载取2 kN·m-2,8层恒荷载取3 kN·m-2,1~7层教室活荷载取2.5 kN·m-2,走廊取3.5 kN·m-2,8层活荷载取2 kN·m-2。
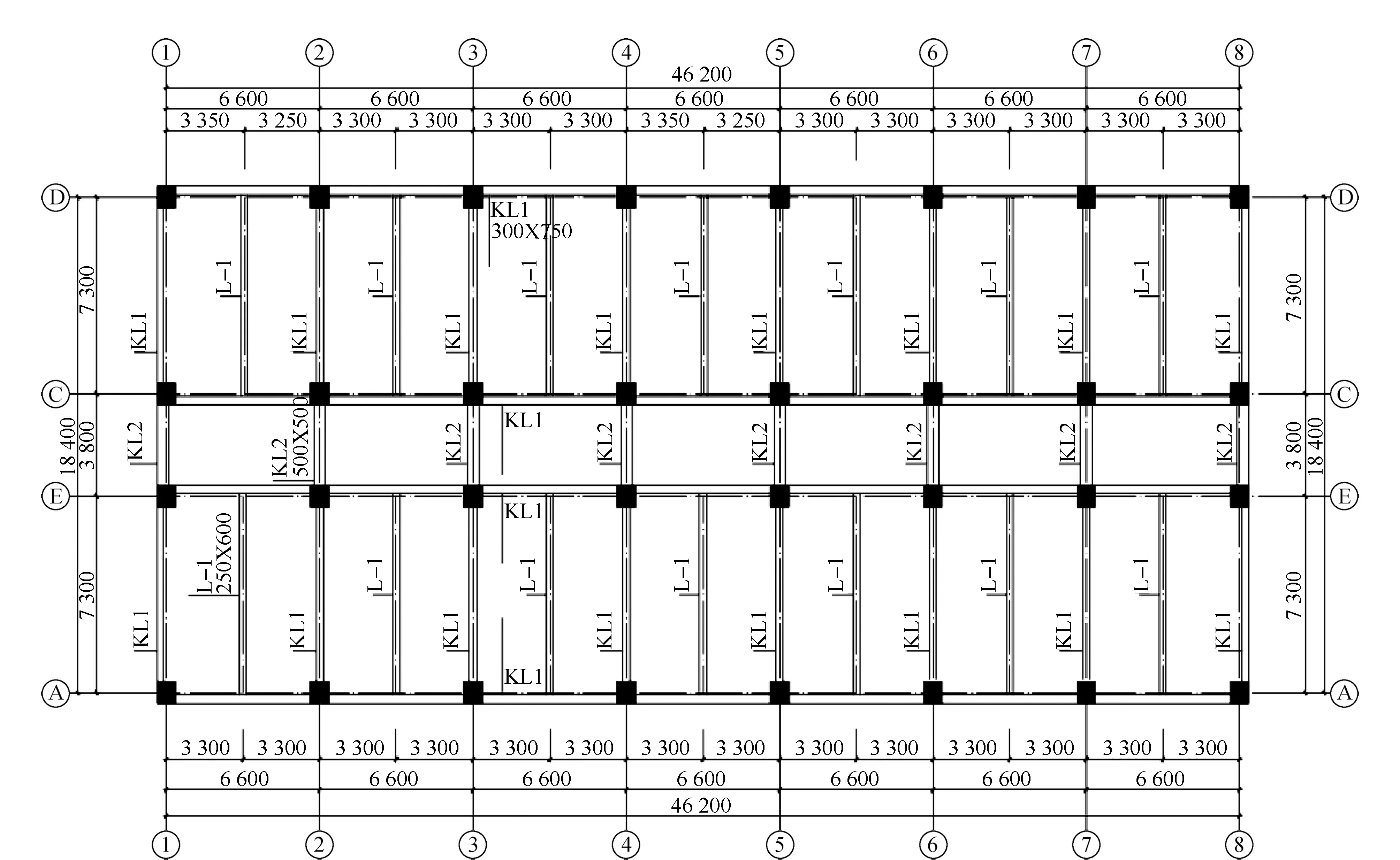
图1 结构平面布置Fig.1 Structural floor plan
选用Opensees材料库中Concrete 02作为混凝土的本构模型,选用Steel 01作为钢筋的本构模型。由于纤维截面可同时考虑弯矩和轴力对截面应力应变关系的影响[7],可提高计算精度,本文建模采用纤维梁单元作为截面类型。通过简化处理,得到一个8层7×3的平面模型,应用Opensees有限元软件建立一榀框架,计算简图见图2。

图2 一榀框架计算简图 Fig.2 Structural drawing of one frame
2 RC框架结构的IDA分析
2.1 IDA分析的原理
RC框架结构的IDA分析最早由Bertero V V[8]提出,分析的思路与Pushover极为类似,因此也被称为DPO。其基本思路为:对结构模型输入多条地震动记录,并将每一条地震动都通过调幅得到不同强度的地震动记录,采用有限元软件进行时程分析得到损伤指标DM的值,所选的地震动强度参数IM损伤指标所构成的曲线即为IDA曲线。若选择一条地震动,则为一条IDA曲线;若选取多条地震动,得到的则是IDA曲线簇。由于得到的IDA曲线簇具有一定的离散性,因此需要做一个分位数曲线来降低其离散程度。本文选用最大增量速度MIV作为IM[7],选用最大层间位移角作为损伤指标DM。
2.2 地震动记录的选取
在地震动记录选取方面,依据建筑结构设计谱进行选择(图3),本文选择的研究对象为实际建筑,具体地震信息见表1。

表1 结构地震信息Table 1 Structural seismic information

图3 结构设计谱 Fig.3 Structural design spectrum
结构设计谱见图3,在美国太平洋地震工程研究中心PEER官网[9],根据建筑结构设计谱进行选择地震动记录,最终选定30条源地震动记录,并对每条地震动进行调幅处理,将每条地震动最大增量速度从0调幅至2 400,每隔100调幅一次,即形成了720条地震动,分别导入Opensees有限元软件中进行后续计算。
2.3 结构极限破坏状态
以最大层间位移角作为损伤指标,参照《建筑抗震设计规范》[10]给出的RC框架结构性能水准及量化指标的容许值,见表2。破坏状态分为基本完好、轻微破坏、中等破坏、严重破坏和倒塌5种,IDA分析以此作为判断结构破坏界限的依据,进而得到结构在不同地震动强度作用下的极限破坏状态。

表2 RC框架结构性能水准的划分Table 2 Division of performance level of RC frame structure
2.4 基于RC框架结构模型的IDA分析
2.4.1 IDA曲线的绘制
依据选取的30条地震动记录,以MIV作为地震动强度指标,每条地震动记录都采用等步长增量的IDA计算方法进行线性调幅,将MIV从0调幅到2 400,将调幅后的地震动记录分别输入到二维模型中,得到30条IDA曲线,构成IDA曲线簇,见图4。
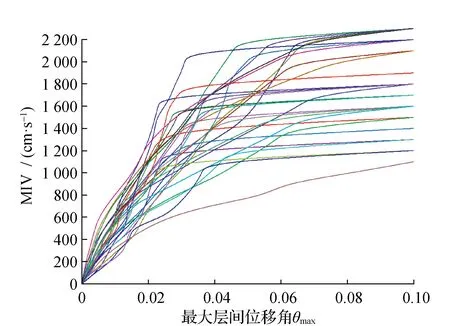
图4 RC框架结构模型的IDA曲线Fig.4 Incremental Dynamic Analysis curve of RC frame structure model
2.4.2 分位数曲线的绘制
为了减少IDA曲线簇的离散性,基于地震强度参数IM统计原则[11],对以上30条IDA曲线进行分位数曲线统计分析,具体分析步骤为:在某个MIV值下,得到一系列的θmax值,分别计算出这一系列θmax的中值μ和对数标准差σ,将(θmax,μ)连接起来构成的曲线则为50%的分位数曲线,将(θmax,μe+σ)连接起来构成的曲线为16%的分位数曲线,将(θmax,μe-σ)连接起来构成的曲线为84%的分位数曲线,见图5。

图5 分位数曲线Fig.5 Quantile curve
由图5可见,当θmax=1/550时,16%分位数曲线对应的MIV=179.088 cm·s-1,50%分位数曲线对应的MIV=115.572 cm·s-1,84%分位数曲线对应的MIV=71.803 cm·s-1。根据上述曲线可得到各性能状态的结构所承受的地震动强度指标MIV,见表3。

表3 不同损伤状态下的MIVTable 3 MIV corresponding to different damage states
3 RC框架结构的易损性分析
3.1 易损性分析的基本原理
结构地震易损性是结构固有的一种属性[12],能够反映结构达到某种极限破坏状态的概率。依据Cornell C A给出的损伤指标DM与地震动强度参数IM之间的统计关系[13]:
DM=a(IM)b
(1)
通常情况下设定结构的损伤指标DM对地震动强度参数IM的概率模型符合对数正态分布[14],对上式两端取对数得
ln(DM)=a+bln(IM)
(2)
式中,a,b为统计回归系数,通过IDA分析得到的数据经过统计回归得到。
假设每条IDA曲线中DM和IM均服从对数正态分布,则结构地震易损性函数[15]为
(3)
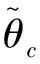
3.2 易损性曲线的建立
将二维模型通过IDA分析得到的数据进行对数线性回归分析,进而得到地震动强度参数IM和损伤指标θmax的关系见图6。
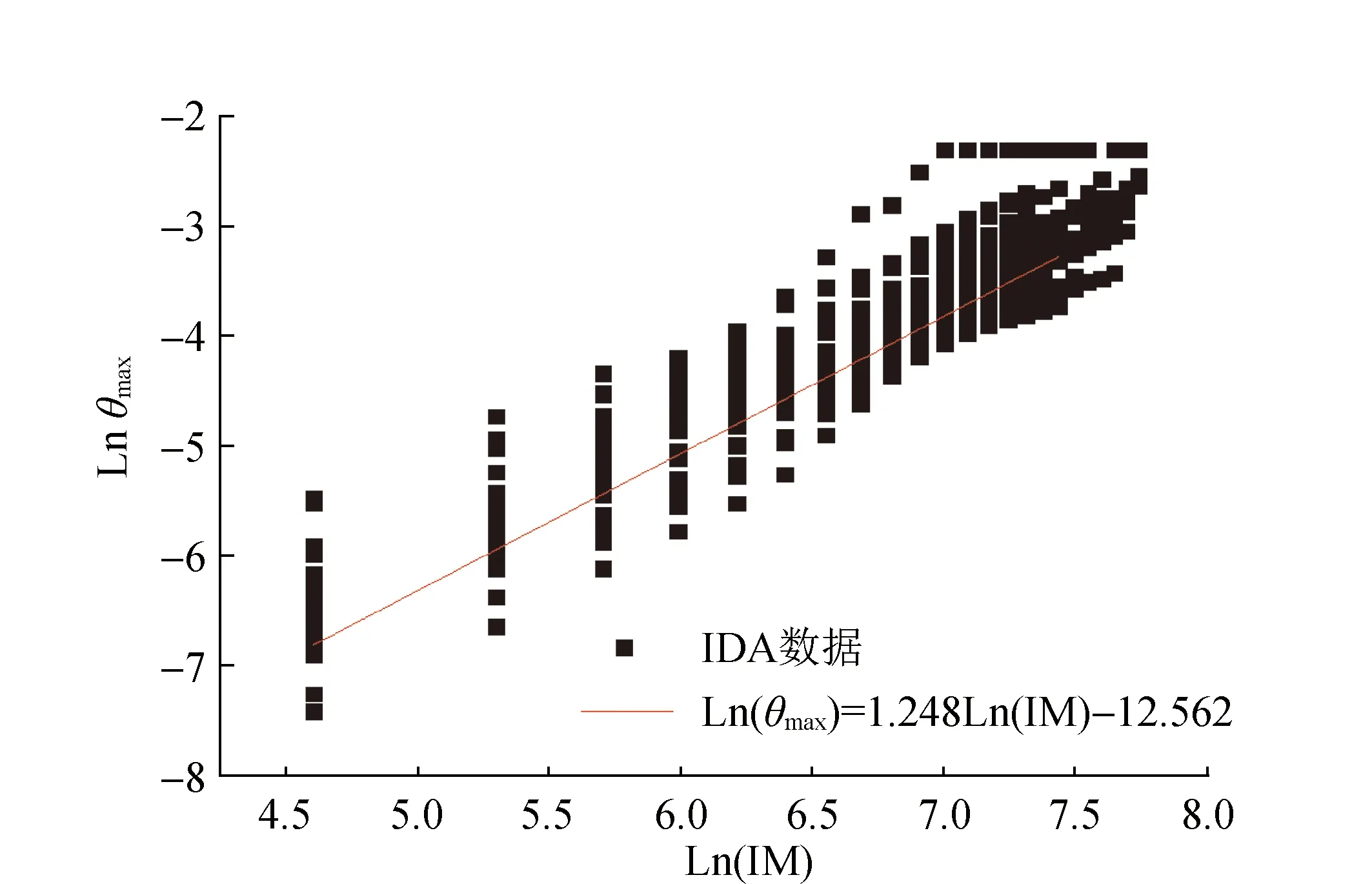
图6 数据拟合曲线Fig.6 Data fitting curve
对散点进行线性拟合,得到易损性函数式为

(4)
相关系数为0.966,平均对数标准差为0.36。
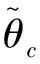

图7 RC框架模型的易损性曲线Fig.7 Vulnerability curve of RC frame model
4 结 论
本文给出了一种基于性能的结构地震易损性分析方法,应用Opensees有限元软件建立8层框架二维模型,提出基于最大增量速度MIV为地震动强度参数指标的易损性分析方法,选取30条地震动记录,对防灾科技学院新建北校区教学楼进行易损性分析,通过建立理论的易损性曲线,得出结构达到不同损伤状态下的MIV限值,进而对其损伤及抗倒塌性能进行评估,为震后结构的安全评估和修复加固奠定了基础,并且为其震害损失预测提供了依据。此外,还可以通过该模型,得到该区域的地震易损性矩阵,用于地区的防震减灾规划。

