空间细长杆-梁结构热致振动分析

冯雨晴，马小飞，王 辉，范 超，王 晶

(1.中国空间技术研究院 西安分院，陕西 西安 710000；2.北京卫星环境工程研究所，北京 100094)

柔性空间结构在轨运行时，会受到太空温变环境的影响，尤其在进出地球阴影区时，外热流会发生剧烈变化，结构受照面与非受照面的温差可达200℃以上[1]。温度的剧烈变化会引发结构产生热致结构响应，按响应的不同情况，可以分为5种[2]：热碾轧、热弹性冲击、热致变形、热致振动以及热颤振。大型柔性空间结构如可展开天线、太阳翼、空间桅杆等具有尺寸大、刚度小的特点[3]，在轨运行时易受到外热流影响，可能产生振动，因此对空间柔性细长杆-梁结构进行热致振动分析是很有必要的。

现有文献中，国内外学者大都使用仿真以及数值模拟方法来计算结构的热振动情况。薛明德等[4]以悬臂梁为研究对象，提出了傅里叶温度有限元法，将温度拆分为平均温度与摄动温度，并计算了在摄动温度引起的热弯矩作用下结构的热致振动响应。SHEN等[5]针对空间可展开结构在展开过程中热载荷对大位移、大旋转结构的影响，提出了一种基于绝对节点坐标的耦合热效应梁模型。孔祥宏等[6]提出了等效位移法，可将温度载荷等效为机械载荷来计算热振动。左亚帅等[7]以低轨运行的卫星-太阳能帆板为研究对象，提出了一种可以分析其在宇宙空间各种热流作用下刚-柔-热耦合动力学特性的建模方法。LIU等[8]考虑了航天器的姿态运动、结构变形与热载荷之间耦合的作用，基于哈密顿原理，建立了刚-柔-热耦合动力学模型。ZHANG等[9]以方形桅杆式太阳帆为研究对象，分析了其在低轨道上的动力学稳定性。张弛等[10]指出针对有阻尼的结构，Boley系数数值不再准确，但总体趋势不变。随着理论的不断成熟，相关的热振动试验也在不断开展。SU等[11]设计实现了我国第一个空间吊杆的热振动试验，试验结果与理论预测十分吻合。FAN等[12]通过对一端固支的细长薄壁管加载与卸载热流，来模拟空间结构进入与离开地影区时的热致振动现象。目前，国内外学者在对热致振动进行基础理论研究时，均以悬臂梁作为研究对象，因此会认为横截面内存在温差是热致振动产生的根源[4]，但SHEN等[13]指出对于复杂的环形天线，热致振动很可能是由轴向温度梯度引起而非横截面内温差引起。对比论点，文献[13]却并未进一步分析论证。

近年来，随着我国航天事业的发展，研究人员在对桁架及绳索等空间结构建模时，由于其横截面较小，经常简化为杆-梁结构[14]，忽略了截面内的温差。以往文献均认为结构横截面内存在温差时才会引起热振动，对空间细长杆-梁结构而言，忽略截面内温差的情况是否也会引起热致振动尚无学者进行研究。在参照大量文献后，笔者认为对于空间细长杆-梁结构，不论杆-梁结构的截面内是否存在温差，只要温度变化可使结构发生变形且温度场快速动态变化，就会产生热振动现象。为此建立了典型“L”形直角梁进行验证：首先建立了其在温度载荷下的热振动方程，考虑到以往在使用等效位移法计算大型复杂空间结构的热致振动时需要花费较长的时间，效率不够高，故基于上述方程提出了空间细长杆-梁结构的等效轴力计算方法；随后将该方法与等效位移法计算得到的结果进行对比，验证了笔者提出方法的合理性与高效性；最后有限元模拟了周边桁架结构在轨的热致振动情况，为环形天线的结构设计提供参考。

1 “L”形细长直角梁热振动方程的建立

为了降低重量，航天结构中经常使用细长杆-梁结构，即结构长度远大于横截面直径，如可展开天线的桁架结构。这些构件可以简化为杆-梁单元结构进行分析，杆单元可以承受轴向力，一般梁单元结构可以承受横向力、轴向力以及弯矩，对杆-梁结构，横截面内可以忽略温度梯度。

图1为两端固支的“L”形等截面直角梁，其中点A、C固支，AB梁与BC梁固接在一起，交点为B。AB梁与BC梁长度为l，横截面积为A，弹性模量为E，密度为ρ，热膨胀系数为αT，截面抗弯刚度为EI。整体笛卡尔坐标系(o，x，y)建立在A点处，且x轴沿着点A指向点B。在后续分析中，采用以下假设：

图1 两端固支“L”形等截面直角梁示意图

(1) 约束直角梁只能在x-y平面内运动；

(2) 不考虑梁的剪切变形，采用Euler-Bernoulli梁假设；

(3) 不考虑阻尼；

(4) 纵向刚度较大，不计梁的纵向振动；

(5) 材料性质不随温度变化。

基于有限元思想，对该直角梁进行单元的划分，共划分为n-1个单元以及n个节点，不同节点可表示为i(1≤i≤n)，节点温度可表示为Ti(t)，如图1所示。直角梁的节点位移可表示为

(1)

其中，ui为各节点沿单元轴向位移；vi为各节点挠度；θi为各节点转角。

单元内的位移插值函数为

(2)

其中，ξ为结构中的几何位置坐标；N(ξ)为形函数矩阵。平衡方程以及力边界条件的等效积分形式Galerkin提法经整合后可得到虚位移方程为

(3)

应力、应变与节点位移的关系可表示为

(4)

其中，B(ξ)为应变矩阵；D为弹性矩阵。将式(4)代入式(3)中，可得：

(5)

(6)

(7)

Ke|BC=(Te)TKe|ABTe，

(8)

Me|BC=(Te)TMe|ABTe，

(9)

(10)

(11)

2 有限元模拟验证理论

针对细长杆-梁结构的热致振动情况，分别采用等效位移法与

上文提出的等效轴力法进行有限元模拟求解比对。

对图1所示的“L”形等截面直角梁，采用圆环截面，基于有限元理论，将该梁共划分100个单元。直角梁初始温度0 ℃，对D点(节点数为28)与E点(节点数为69)分别施加半正弦波温度冲击，其他节点温度保持0 ℃不变。为了显示出较为明显的振动，温度冲击如下所示：

(12)

其中，ω1为直角梁一阶固有圆频率；T为温度，单位为℃；t为时间，单位为s。温度冲击的载荷曲线如图2所示。结构几何尺寸与材料参数如表1所示。

图2 温度冲击载荷曲线

表1 “L”形等截面直角梁几何与材料参数

计算得到结构的前10阶固有频率如表2所示，可以看出一阶固有频率f1=82.891 Hz，故ω1=520.820 rad/s。

表2 直角梁前10阶固有频率

等效位移法本质为假设温度载荷引起的变形与外力引起的变形相同，即可将温度载荷等效为外力进行加载求解[6]。使用上述已知条件并采用等效位移法进行求解，可以得到点B沿x、y方向准静态位移、动态位移以及幅频响应曲线，如图5所示。

2.1 等效轴力法求解

当D点与E点温度发生变化时，根据式(11)计算得到D点左右相邻两节点F、G以及E点左右相邻两节点H、J对应的等效热轴力变化曲线，如图 3所示，CFx指加载的集中力沿x方向，CFy指加载的集中力沿y方向，正值表示沿图 1中x/y正方向。随后，将计算得到的4个等效热轴力加载至结构上并进行动力学求解。

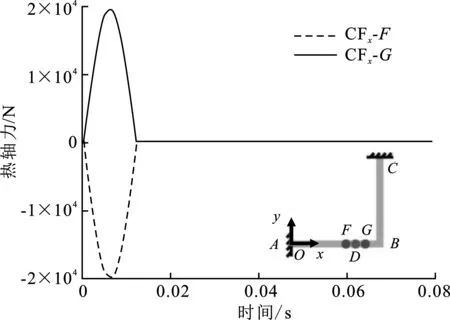
(a) D点温度变化等效为x方向热轴力

图4为t=π/ω1即温度最高点时直角梁结构的准静态位移云图。可以看出：在温度冲击载荷作用下，直角梁发生了伸长弯曲变形。由于AB、BC梁温度的升高，轴向长度均有一定的伸长，AB、BC梁也发生了一定程度的弯曲，AB梁沿y方向发生弯曲，而BC梁则沿x方向发生弯曲；在变形过程中，当t=π/ω1=0.006 03 s时，B点同时达到x、y方向的最大准静态变形，此时U1，max=6.699×10-5m，U2，max=-9.957×10-5m。

图4 t=π/ω1时直角梁准静态位移云图

由于B点处于AB梁与BC梁的交接点，较为特殊，故取B点讨论其热致振动情况。从图5可以看出：热致振动是在准静态变形的基础上叠加周期性振荡运动而成；直角梁在温度冲击载荷作用下，x、y方向均发生了热致振动的现象，且该振动的主要频率为1 015.6 Hz和1 230.4 Hz，与之对应的为第8和第10阶固有频率，x、y方向的振幅量级均为10-6m。

(a) B点x方向两种方法位移对比

2.2 两种方法结果比对

综合图5与表3的计算结果可以看出：等效位移法与文中的等效轴力法得到的x、y方向准静态位移曲线、动态位移曲线、振动频率以及振幅都具有高度的重合性，位移误差控制在0.002 2%以内，即使用等效轴力法计算得到的结构热致振动情况是正确的。对于截面内无温差的柔性细长杆-梁结构，在温度冲击载荷作用下，由于热胀冷缩效应，结构在等效热轴力作用下发生一定的伸长缩短热变形，在不同构件的交接处，由于相互作用，构件会产生一定的弯曲变形，此时容易发生热致振动现象，且振动的频率不一定为一阶固有频率。除此之外，使用同一台电脑，在同等精度条件下计算该“L”形结构热致振动情况，使用等效位移法需要42 min 20 s，而使用笔者提出的等效轴力法则仅需要9 min，节省了约79%的时间。研究中经常使用算法运行的时间来评价计算成本以及算法的复杂性[15]，因此等效轴力法具有更高的效率。值得注意的是，等效轴力法具有一个前提：结构至少由两个相连且不在同一直线上的杆件组成。正是由于杆件间的相互作用力才引起结构的弯曲变形以及热振动，因此，该方法不适用求解单根悬臂梁在热流冲击下的热致振动情况。

表3 两种方法位移计算结果比对

3 计算实例分析

周边桁架为环形可展开天线的刚性支撑结构，在轨展开后，可以抵抗弯矩、扭矩以及剪力的作用，因此可以采用梁单元对其进行分析。研究表明，周边桁架结构在环形天线的前两阶振型中起主要作用，桁架结构模态振型与整个天线的模态振型相似[13]，故研究周边桁架结构在轨热致振动具有一定意义。桁架结构梁单元模型如图6所示，几何参数、材料参数见表4。为计算桁架结构真实在轨的热致振动情况，首先对其进行在轨温度场计算，随后将温度数据作为已知条件代入热振动分析，即采用温度场与变形场顺序耦合的方法分析结构热致振动情况，这种耦合方法虽不如温度场与变形场直接耦合方法精确，但在热变形对温度场影响较小时，可以较为真实地反映结构热致振动的大小与趋势，具有一定的工程意义。该桁架结构运行于太阳同步轨道，最小高度600 km，轨道周期5 792 s，此时太阳位于春分点，+Y轴指向地心方向，+X轴为速度方向。

表4 周边桁架结构几何与材料参数

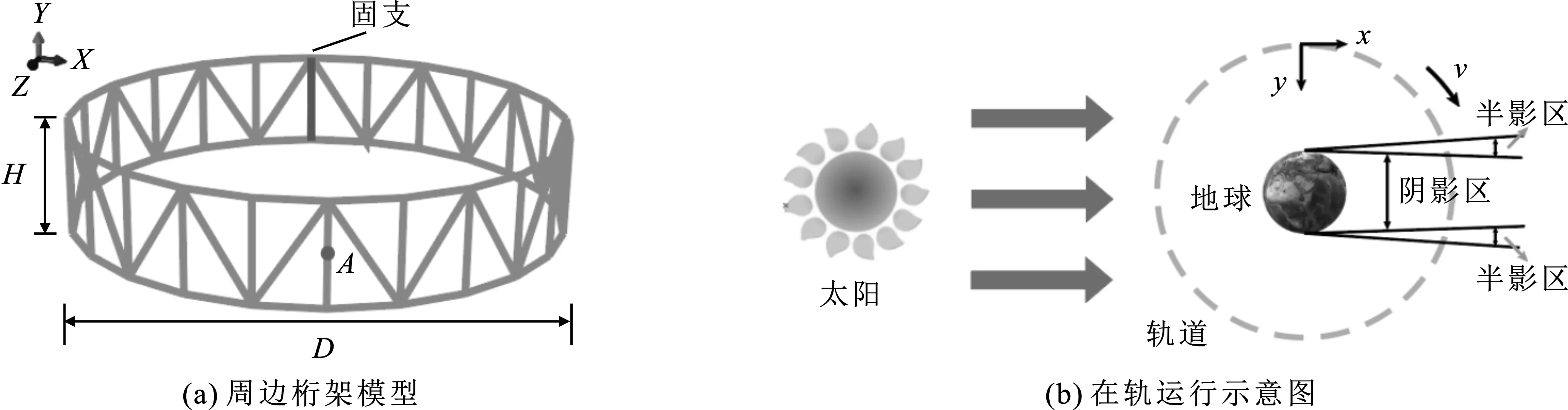
图6 周边桁架模型及其在轨示意图

从图7(a)、(b)中可以看出：周边桁架在太阳同步轨道运行一个周期时，温度在-77.1 ℃～23.1 ℃之间变化，变化区间为100.2 ℃；其中特定点A点(图6所示)一个周期内温度在-76.1 ℃～3.1 ℃之间变化，由于升交点当地时间为0点，故A点温度整体呈现先降后升再降的过程，中间局部温度的降低是由附近杆件的遮挡引起的。

从图7(c)、(d)、(e)、(f)可以看出：由于A点温度的变化，在热胀冷缩效应下，A点沿y方向位移发生了变化，但对比图7(b)、(d)，发现y方向位移与温度变化趋势并不一致，这说明不可忽略A点附近节点对A点的作用力；A点在x、z方向均发生弯曲，这是由于周围杆件对其有x、z方向的作用力；A点在x、y、z方向上均发生了热致振动现象，x方向主要发生一阶振动，振动频率为0.294 99 Hz，振幅为10-7m量级；y方向主要发生二阶振动，振动频率为0.511 72 Hz，振幅为10-7m量级；z方向主要发生三阶振动，振动频率为0.828 79 Hz，振幅为10-8m量级，但整体来看，结构主要是沿x方向的一阶振动，是由与A点所在杆相连的其它杆对A点所在杆的作用力引起的弯曲振动。因此，由细长杆-梁结构组成的周边桁架结构在轨运行时，也会发生热振动现象，进一步证实了研究结论。

(a) 一个周期内温度变化图

4 结束语

笔者对空间细长杆-梁结构进行了热致振动分析，得到了以下结论：

(1) 验证了即使杆-梁结构的截面内不存在温差，只要温度变化可使结构发生变形且温度场快速动态变化，就会产生热振动现象；

(2) 以“L”形直角梁为对象，基于结构温度变化，推导了等效热轴力引起的热振动方程，提出了等效轴力计算方法，并在“L”形直角梁算例中将文中方法计算结果与等效位移法结果进行比对，误差在0.002 2%以内，但笔者提出的方法计算时间缩短了约79%，证明该方法是正确与高效的；

(3) 对于空间细长杆-梁结构，由于杆件之间的相互作用力，会导致结构弯曲变形，因此在太空环境下，会发生热致振动；

(4) 环形可展开天线的周边桁架结构在轨运行时，会发生热致振动现象，对于口径10 m的桁架，热变形量级为10-4m，振幅量级为10-7m。对于未来高精度需求的环形天线，为保证天线的精度，需要控制结构表面温度以及采取一定的减振措施。

笔者提出的计算方法可以为截面较小、近似可忽略截面内温差的柔性空间细长杆-梁结构提供一定的借鉴与参考。