能量收集多天线发送机的功率控制和天线选择

宁晓晗，雷维嘉

(1.重庆邮电大学 通信与信息工程学院，重庆 400065；2.重庆邮电大学 移动通信技术重庆市重点实验室，重庆 400065)

随着无线通信服务空前的增长，网络和终端设备的能耗不断提高，“绿色通信”成为近年来通信领域研究的热点问题，收集和利用周围环境中的能量是其中的重要问题之一。太阳光、风、振动、运动、电磁波，都可以成为能量的来源[1]。收集的能量可以作为采用电网和电池供电的通信系统的能量补充，或独立作为设备能量的来源，减少对电网或电池能量供应的依赖，提高经济和生态效益。与常规能源不同，可再生能源一般具有间歇性和随机性，使得采用能量收集(Energy Harvesting，EH)方式供电的系统在能量使用上面临新的挑战。作为一个影响系统性能的重要因素，能量收集无线通信系统中的功率使用和分配策略是目前无线通信学术界研究的重要课题之一。

能量收集设备供电的无线通信系统中，发送端的功率控制算法可分为离线和在线功率控制算法两类。在离线功率控制算法中，发射机预先知道能量到达、数据到达和信道状态的全部信息。有较多的文献对不同系统模型下的离线功率控制算法进行了研究。文献[2]针对两个传感器都由能量收集装置供电的通信系统中，最小化系统传输信息失真加权和的问题，在事先已知能量到达情况的条件下，将问题进行转换后利用拉格朗日乘数法对优化问题进行求解。文献[3]同样研究传感器配备能量收集装置的通信系统中系统信息年龄、失真加权和最小化问题，在已知能量到达过程的条件下，提出了一种离线广义后向注水功率分配的算法。文献[4]针对能量收集的认知中继通信系统中的吞吐量最大化的中继功率控制问题，将多变量优化问题转为单变量优化问题，再通过拉格朗日对偶法求解得到吞吐量最大化的离线功率控制策略。与离线策略理想化的假设不同，在线功率控制算法不依赖于未来信道状态、能量到达情况的确定信息，更具有实用性。如文献[2]在提出离线注水算法的基础上，进一步考虑信息随机到达的情况，使用代价函数将问题进行转换，提出了一种仅基于当前时隙代价函数值的在线迭代算法。文献使用马尔科夫过程对无线通信系统的状态进行建模，再通过动态规划等算法求解优化问题是相关文献中解决在线功率控制问题常用的方法。如文献[3]进一步考虑已知能量到达的统计信息的条件下，将信息年龄建模为马尔可夫过程，再利用强化学习算法求解问题。文献[5]在发射端已知能量到达和信道衰落、数据到达的统计信息的条件下，将能量到达和信道衰落的随机变化建模为马尔可夫过程，再利用State-Action-Reward-State-Action算法求解长期时间平均能量效率最大化的功率控制问题。文献[2-3，5]中提出的在线功率控制算法需要获得能量到达和信道衰落的统计信息，且计算复杂度较高。近几年也有文献对使用不需要系统状态统计特性的李雅普诺夫优化框架[6]来解决能量收集无线通信系统中的功率控制问题进行研究。李雅普诺夫优化框架的基本特征是在保持队列稳定的同时对优化对象进行优化，通过将约束条件转换为虚队列的长期稳定性要求来简化优化问题的求解。文献[7]针对源节点具有能量收集装置且电池容量有限的点对点通信系统，在仅知当前能量和信道衰落状态的情况下，提出一种基于李雅普诺夫优化框架的在线功率控制算法，该算法具有较低的复杂度。在文献[7]的基础上，文献[8]研究块衰落信道下的半双工两跳放大转发中继网络中，最大化平均传输速率的源节点和中继节点功率的联合控制问题。文献将源节点和中继节点的电池电量约束转换为虚队列的稳定问题，使用李雅普诺夫优化框架对优化问题进行转换后求解。文献[9]针对发射机由电网和能量收集装置混合供电的传输系统，以电网能量消耗最小化为目标，对发射机的功率和传输调度进行优化控制，将数据队列的时延约束转换为虚队列的稳定问题，同样使用李雅普诺夫优化框架对优化问题进行转换后求解。文献[10]针对中继由能量收集装置供电的半双工两跳解码转发中继系统，利用李雅普诺夫优化框架求解最小化源节点长期平均能耗、最大化平均传输速率的源和中继节点发送功率的联合控制问题。在能量收集通信系统功率控制的相关文献中，多数都未考虑电路功耗问题，一般假设收集的能量仅用于信号的发送，忽略了射频链路、处理电路等的功耗，仅有少部分文献在功率控制的研究中考虑了电路功耗。文献[11-12]针对大规模天线基站由电网和能量收集设备联合供电的下行传输系统，以能源成本最小化(也即电网能量消耗最小化)为目标，对基站的发送功率和发送天线进行优化控制，研究中考虑了射频链路的功耗和信号处理电路的功耗。其中，文献[11]在用户服务质量的约束下，在离线条件下迭代搜索最优的天线组合，采用非线性分式规划和拉格朗日乘数法求解给定天线组合方案下的发送功率优化问题。文献[12]则采用非线性分式规划和李雅普诺夫框架对原始的优化问题进行转换，并对转换后的优化问题进行求解，最后采用二分法搜索和拉格朗日对偶分解法得到在线的优化算法。

现有的相关文献中，在进行功率控制的优化时，一般都忽略了设备信号处理与变换电路的功耗，系统能量消耗仅限于信号辐射。实际上，在低发射功率的设备中，电路功耗并不明显低于信号发射功耗。对于单天线的发射机而言，电路功耗可近似认为是一个常数，只需在总功耗上增加一个常数项，简单地进行一些调整就可使用现有的未考虑电路功耗的功率控制方案。而对于多发送天线的系统而言，电路功耗则与激活的天线数有关。激活的发送天线越多，获得的发送天线阵列增益越大，但电路功耗也越大，激活天线也成为一个需要优化的对象。此时，现有的未考虑电路功耗的功率控制方案经过简单的调整后并不能获得最优的性能。考虑到多天线的能量收集的发送机中电路功耗不能忽略的场景，研究以最大化长期平均传输速率为目标的功率控制和发送天线选择的联合优化问题。系统模型中包括一个配备有能量收集装置和可充电电池的多天线源节点，以及一个单天线的目的节点。每时隙源节点需要根据电池电量和信道状态来选择合适的发送天线和传输功率。在能量到达过程随机、信道为时变衰落信道条件下，通过李雅普诺夫框架求解每时隙的发送功率和天线选择问题，最大化长期时间平均传输速率。为解决该优化问题，将收集能量的使用约束通过保持虚队列稳定来满足，使用李雅普诺夫优化框架将长期时间平均的优化问题转换为一个每个时隙的漂移加惩罚函数最小化问题，并求解。与文献[11-12]的基站采用电网与收集能量混合供电的系统模型不同，笔者设计的发送机完全由收集的能量供电。相比较文献[11]的高复杂度、依赖于能量达到的统计信息的算法，笔者给出的是一种低复杂度的、不要求任何信道状态和能量到达统计信息的在线算法。相比较同时应用了李雅普诺夫框架的方法[12]，笔者在对问题进行转换时使用了不同的方法，转换后的问题求解复杂度更低。

1 系统模型

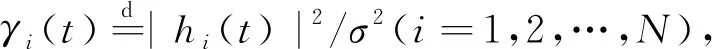
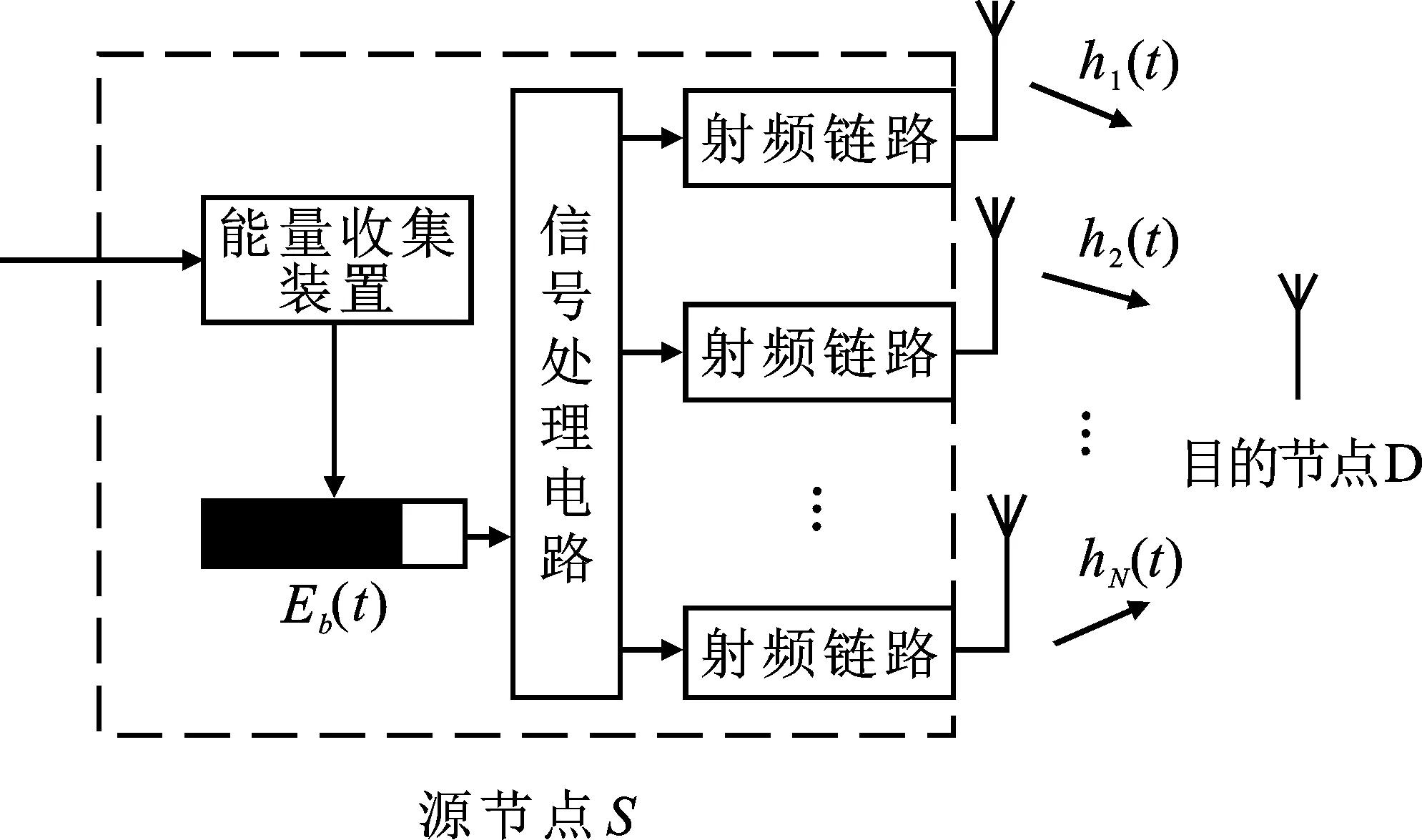
图1 系统模型

记电池存储电量最大为Emax，最小电量为Emin。为避免电池损坏，延迟电池寿命，一般要求电池电量不应耗尽，即Emin> 0。时隙t电池中存储的电量为Eb(t) ，有Emin≤Eb(t)≤Emax。设电池最大充电速率和放电速率分别为Pc，max和Pd，max。

假设时隙t激活了瞬时信道质量最好的M根天线发送信号，发送机消耗的总功率P(t)为

P(t)=PT(t)+MPa+Pc。

(1)

总功率需满足电池的最大放电速率的约束，即

0≤P(t)≤Pd，max。

(2)

每时隙t内消耗的总能量不能超过该时隙开始时电池存储的可用电量，即

0≤ΔtP(t)≤Eb(t)-Emin，

(3)

其中，Δt为一个时隙的时长。

设时隙t能量收集设备从环境中收集的能量为Ea(t)，充入电池的电量为Es(t)，其同时受到电池的剩余空间和最大的充电速率的限制，即

Es(t)=min{Emax-(Eb(t)-ΔtP(t))，Ea(t)，ΔtPc，max} 。

(4)

每时隙收集的能量充入电池，同时电池提供传输信号所需的能量，电池电量的动态方程为

Eb(t+1)=Eb(t)-ΔtP(t)+Es(t) 。

(5)

时隙t的信道容量为

(6)

其中，Φ(t)表示时隙t激活天线的集合，M为Φ(t)中的天线数量。

2 优化问题构造和求解

传输速率与各信道的衰落情况、源节点传输信号的功率和天线选择有关，而可用传输信号的功率受到电池电量、电路功耗等的约束，传输速率最大化问题是在电池电量长期稳定的条件下传输信号功率和天线选择的联合优化问题。

2.1 优化问题构造

在发送端配备多天线时，在信号发送总功率一定的条件下，发送天线越多，获得的阵列增益越大，传输速率越高。但激活的发送天线数越多，射频链路电路功耗越大。在可用能量一定的条件下，激活天线越多，则用于信号发送的功率就越小。因此，应根据信道状态和可用能量状态，在电池操作约束和电量更新约束下，合理选择激活的发送天线和信号发送总功率，获得尽可能高的平均传输速率。优化问题可表示为

(7)

其中，式(2)为最大放电功率约束，式(3)为电池存储电量对总功率的限制，式(5)为电池电量变化的约束，E[x]表示期望运算。由于能量收集、信道状态是随机变化的随机过程，因此P1是一个随机优化问题。

式(5)可改写为

Eb(t+1)-Eb(t)=Es(t)-ΔtP(t) 。

(8)

从0到T-1时隙，将式(8)左右两端叠加后求期望，有

(9)

在式(9)两端除以T，并取T→∞的极限，且电池容量受限，式(9)左端为有限值，因此有

(10)

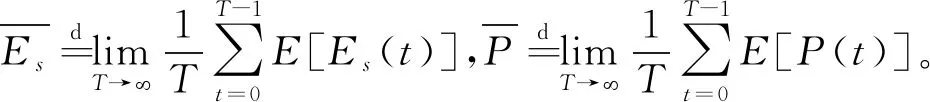
(11)

2.2 优化问题的转换

采用李雅普诺夫优化框架求解优化问题P2。在李雅普诺夫优化框架中，可以通过保持虚队列稳定来满足约束条件。定义描述电池状态Eb(t)的能量虚队列为

X(t)=Eb(t)-A，

(12)

其中，偏移量A是一个正常数。偏移量A的设置是为了在采用李雅普诺夫框架优化后使电池中的电量在一个适当的水平上波动，以适应信道衰落和能量收集量的随机变化。

若保持虚队列稳定，则约束条件式(10)满足，可通过使队列漂移最小化实现队列稳定。定义李雅普诺夫函数为

(13)

用李雅普诺夫漂移描述李雅普诺夫函数从一个时隙到另一个时隙的变化情况，其定义为

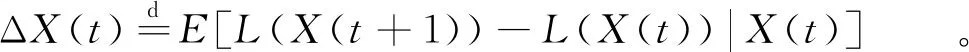
(14)

显然，李雅普诺夫漂移越小，时隙间队列长度的变化越小，队列长度越接近于0，队列越稳定。为了在保持虚队列稳定的同时最大化长期时间平均传输速率R(t)，将R(t)的负定义为惩罚项，与李雅普诺夫漂移一起构成漂移加惩罚，即

ΔX(t)-VE[R(t)|X(t)] 。

(15)

若能使漂移加惩罚最小化，则就在保持虚队列稳定的同时最大化了传输速率。漂移加惩罚式(15)的V是一个权衡虚队列稳定性和速率最大化的非负权重。权重V较大时，优化偏重于最小化惩罚项，即偏向于速率最大化；V较小时，则倾向于最小化虚队列漂移，电池电量的稳定性更高。

漂移加惩罚项(15)有一个上界，可以通过最小化这个上界实现漂移加惩罚项的最小化。根据X(t)的动态方程，有

X(t)E[Es(t)-ΔtP(t)|X(t)] 。

(16)

由式(3)和式(4)可知Es(t)、ΔtP(t)有限，上式等号右边第1项是恒大于或等于0的有限值。在充电量Es(t)为最大充电速率约束下的最大值ΔtPc，max，且不发送信号，或者充电量Es(t)=0，且发送机总功耗为最大放电速率约束下的最大ΔtPd，max时，取得最大值，即

(17)

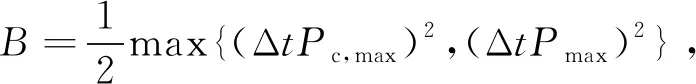
ΔX(t)-VE[R(t)|X(t)]≤B-VE[R(t)|X(t)]+X(t)E[Es(t)-ΔtP(t)|X(t)] 。

(18)

此即漂移加惩罚函数的上界。其中，常数项B与优化变量{P(t)，Φ(t)}无关，可将其从优化函数中移除。由于已经通过保持电池虚队列稳定满足长期时间平均约束式(10)，将其从P2问题的约束条件中移除；在当前信道状态和电池状态已知的条件下，将长期平均性能的优化问题改为在每时隙的优化问题，优化问题P2转换为

(19)

2.3 优化问题的求解

问题P3是天线选择和功率的联合优化问题，由于天线数只能取整数，故不能直接进行解析求解。因天线数量有限，笔者首先采用遍历所有可能的激活天线集合，对每个激活天线集合优化发送功率，然后选择使漂移加惩罚项最小的激活天线集合及其对应的功率组合作为优化问题的解。由于总是选择瞬时信道质量最好的天线发送信号，故每一个激活天线数下只有一种天线选择方案，因此总的激活天线集合数目即为天线数N，遍历的复杂度不高。

定义P3问题中激活天线数为M时的目标函数为

(20)

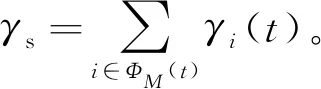
(21)

(22)

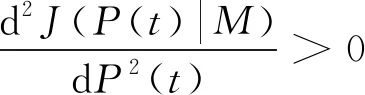
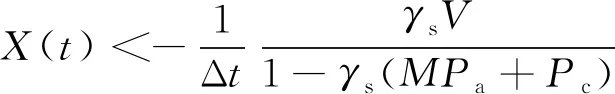
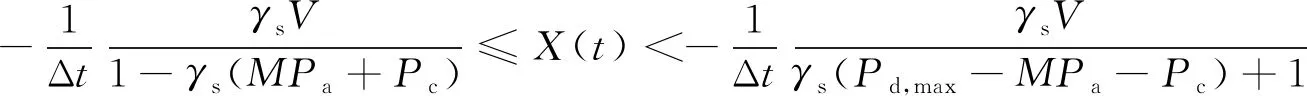
(23)

易得

(24)

由于J(P(t)|M)对P(t)的二阶导为正，故该极值点为极小值点。进一步考虑电池最大放电功率和可用电量的约束，最优功率为Popt(t)=min(P*(t)，Pd，max，Eb(t)/Δt)。

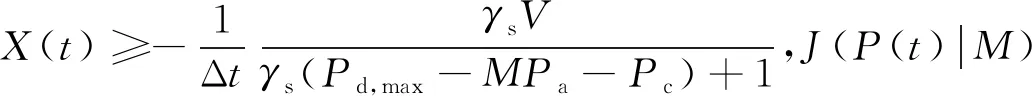
Popt(t)取值归纳如下式：

(25)

得到每个激活天线数M下的最优功率Popt(t)后，再计算各天线数下的漂移加惩罚，选取使漂移加惩罚项最小的天线数及其对应的最优功率作为该时隙的天线选用和功率方案。

2.4 复杂度分析

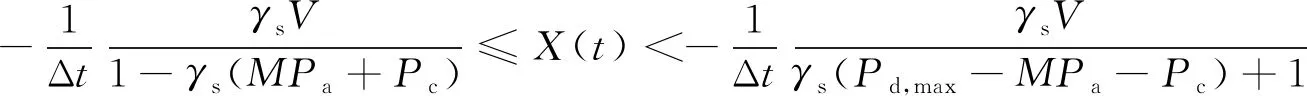
3 仿真结果

3.1 参数设置

上述算法在信道状态发生较为明显的变化时，需重新对发送功率进行更新，时隙长度应与信道相干时间相关，为简便起见，仿真中，时隙长度设置为Δt=1 s，仿真时长T=5×104s。除非特别指出，仿真的参数设置如下：发送端的天线数N=8；每时隙能量到达量Ea(t)服从均匀分布的复合泊松过程，泊松分布到达率为λ=0.5单位/时隙，每个单位的能量服从[0，0.6]之间的均匀分布。仿真参数：Emin=2J，Emin=50J，Pc，max=5W，Pdmax=5.5W，Pa=0.01W，Pc-0.05W，信道为瑞利衰落信道，各信道系数均为服从均值为0、方差为1的复高斯分布随机变量；信道系数在一个时隙内保持不变，时隙间随机独立变化；电池的初始能量为25 J，电池电量虚队列的偏移量设置为A=40，权重V=5。

3.2 与对比算法的性能比较

为了比较文中算法的性能，将其与全功率贪婪算法、半功率算法、激活天线数固定的方案进行对比。① 全功率贪婪算法(Greedy Algorithm，GA)：每个时隙源节点均根据电池中可用电量的最大值或最大放电功率来设置总功率，即P(t)=min(Pd，max，(Eb(t)-Emin)/Δt)。遍历所有的天线数，即M=1，2，…，N，选择瞬时信道质量最好的天线为发送天线，计算相应的传输速率，其中的最大值为该时隙下的传输速率。② 半功率算法(Half Power Algorithm，HPA)：该算法与全功率算法类似，不同之处在于每个时隙源节点均以电池中可用电量的一半设置使用总功率，即P(t)=min(Pd，max，(Eb(t)-Emin)/(2Δt))。③ 天线数固定算法：每时隙取相同数量的、信道增益最高的天线发送信号，选用天线数量为2根、4根、6根或8根，然后采用与文中相同的方法确定发送功率。

图2为源节点配备天线数N为4和8时，文中算法、GA算法、HPA算法的平均速率随着时间变化的仿真结果，每时隙的平均速率为从仿真开始到当前时隙各时隙速率的平均值。图3给出了配备天线数N为8时的3种算法源节点电池电量的时间轨迹图。文中算法根据信道和电池能量状态确定发送天线数和功率，电池电量基本维持在偏移量附近，能较好地适应信道状态和能量收集量的随机变化。而GA和HPA算法的电量始终维持在较低水平，每时隙的发送功率决定于上一时隙收集的能量，不能根据信道状态进行发送功率的调度。因此，文中算法的性能明显高于GA、HPA算法，N=8时，相比HPA算法有约40%的优势，相比GA算法有约40.23%的优势；N=4时，相比HPA算法有约51.59%的优势，相比GA算法有约50.20%的优势。3种算法都是配备的天线数越大，传输速率越高。

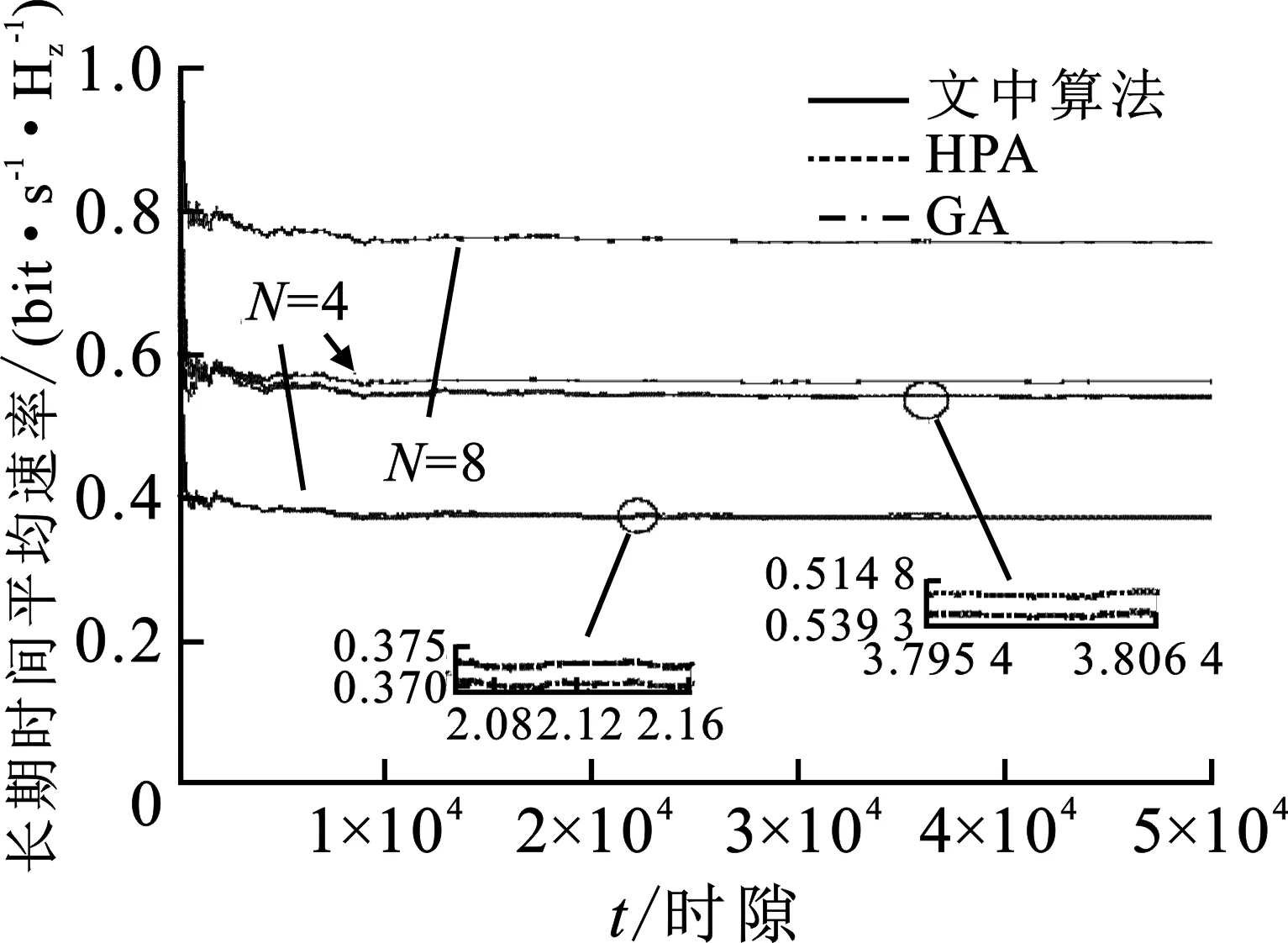
图2 平均速率的比较

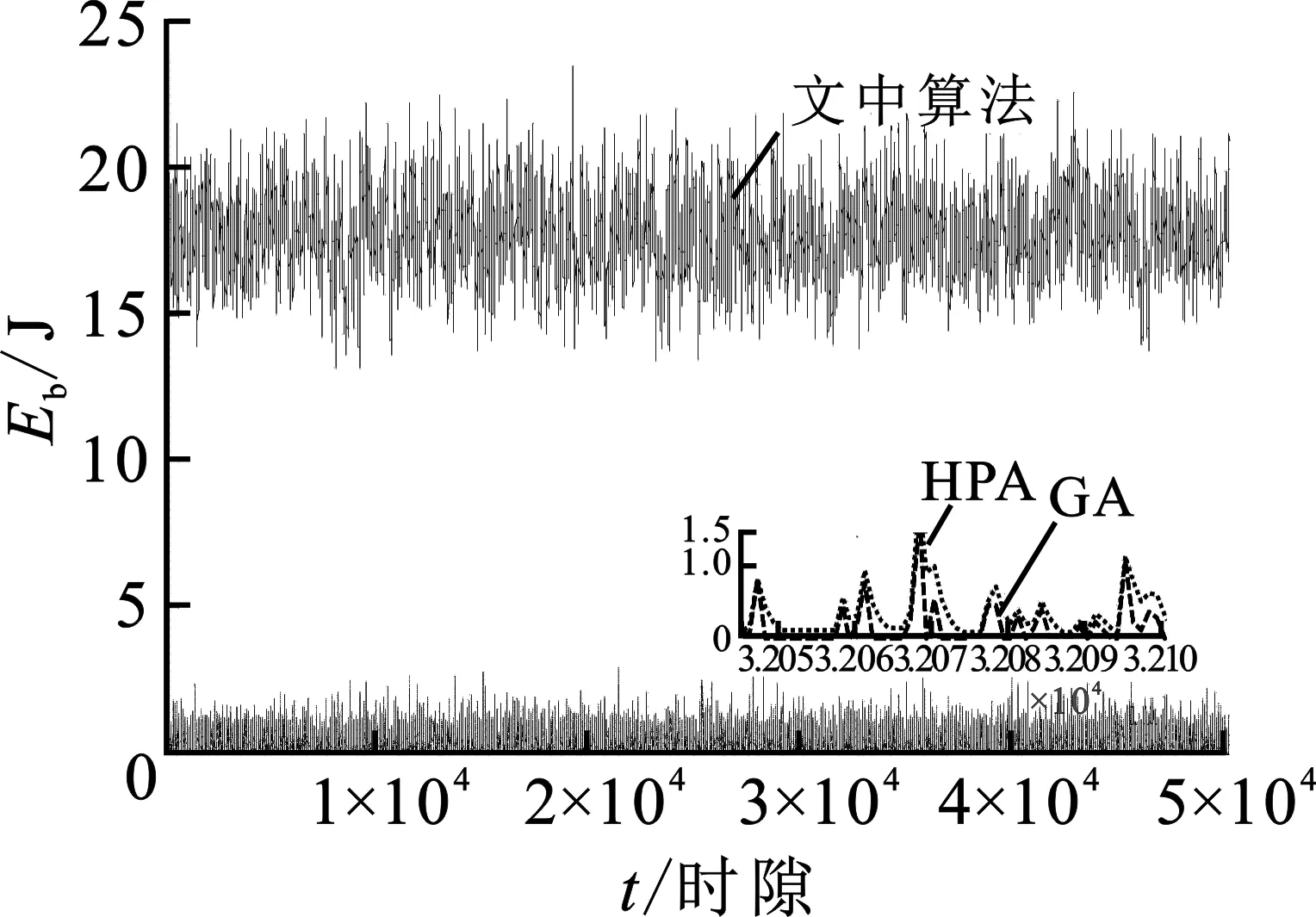
图3 源节点电池电量时间轨迹

图4给出了文中算法与发送天线数固定取值的方案的性能对比。观察发送天线数固定为2、4、6、8的平均传输速率，可以看到并不是使用的天线数越多越好，也不是越少越好。选用的天线数越大，阵列增益也越大，但激活的射频电路功耗也越大，在总功率一定的情况下，信号的发送功率也越小，天线数过多时，阵列增益增大带来的好处并不能完全弥补发送功率减小带来的性能损失，反而会引起传输速率的下降。而天线数过少时，尽管射频电路功耗较少，但传输性能较差，也不能获得更高的传输速率。而文中方案根据能量和信道状态，选择合适的发送天线数和发送功率，能在阵列增益和射频电路功耗间进行平衡，因此能获得最高的传输速率。

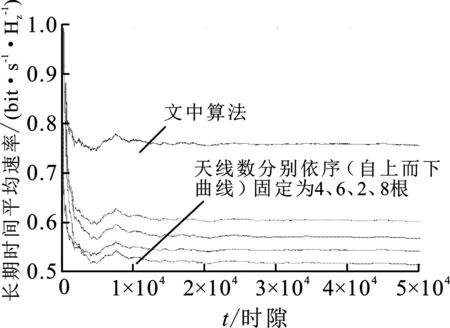
图4 与固定天线数算法的性能比较

3.3 参数变化对速率的影响

图5给出了源节点配备天线数N变化时，文中算法能获得的平均速率的仿真结果。可以看到，随着天线数增加，系统的传输速率也在增加。虽然每个时隙不会选择激活所有的天线，但是天线数越多，即使是激活相同数量的天线，从统计上来看，激活天线信道的质量会更高，因此能获得更高的传输速率。

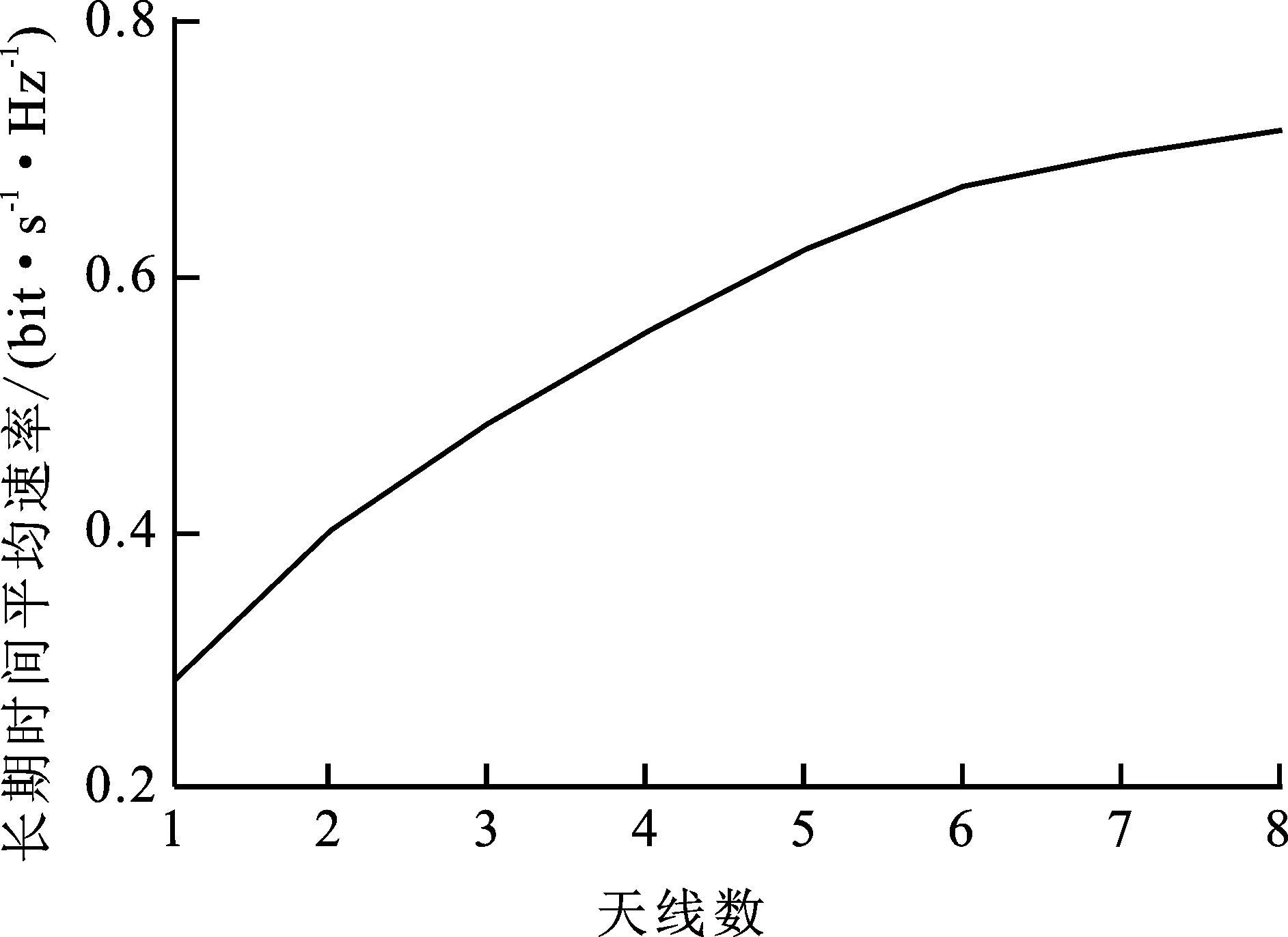
图5 长期时间平均速率与天线数的关系

图6给出了权重V对系统性能影响的仿真结果，图中的数据是整个仿真中各时隙的电量和传输速率的平均值。从图6(a)可见，随着V的增加，源节点更倾向于最大化传输速率，每时隙会选择更大的功率，因此电池平均电量降低；相应地，在权重较小时，速率会随着权重的增大而增加，但速率的增加会逐渐减缓，如图6(b)所示。当权重V增加到10以后，速率反而随V的增加而下降。这是因为在权重较小时，权重增加虽然使平均电池电量下降，但电池电量仍然足够高，仍能支持大的发送功率，同时权重增加使得优化更偏重于速率最大化，因此传输速率能随V的增大而提升。当权重增加到10以后，电池的电量过低，不能支持信道条件较好时的高发送功率，对信道的利用率下降，因此速率反而下降。

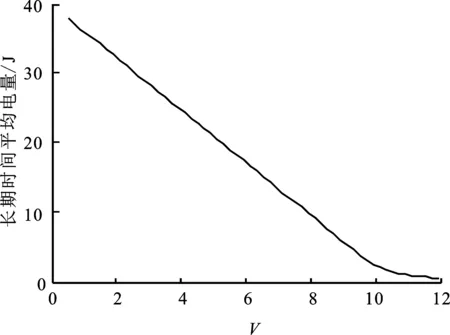
(a) 平均电池电量

图7(a)、(b)给出了能量虚队列偏移量A变化时系统性能变化的情况。可以看出，随着偏移量A的增加，电池中保留的平均电量不断增加；平均速率在A小于20时随着偏移量的增加而增加，但当偏移量到达20以后，传输速率基本不再随A的增大而变化。这是因为当偏移量较小时，随着偏移量增加，电池中保留的电量增加，能够支持的最大发送功率增大，能在信道状态较好时以较多的发送功率传输信号，能更好地利用信道的传输能力。在电池电量足够高后，继续增加偏移量使平均电池电量提高并不能使传输速率继续增大，这是因为每时隙的最大功率还受到电池最大放电速率的限制，同时平均功率还受到电池电量稳定性要求的限制(也受到能量收集量的限制)。而在偏移量过大后，会导致电池的剩余存储空间减小，在能量达到量较大的时隙发生能量溢出而导致能量损失的可能性增加，因此传输速率反而会有轻微的下降。

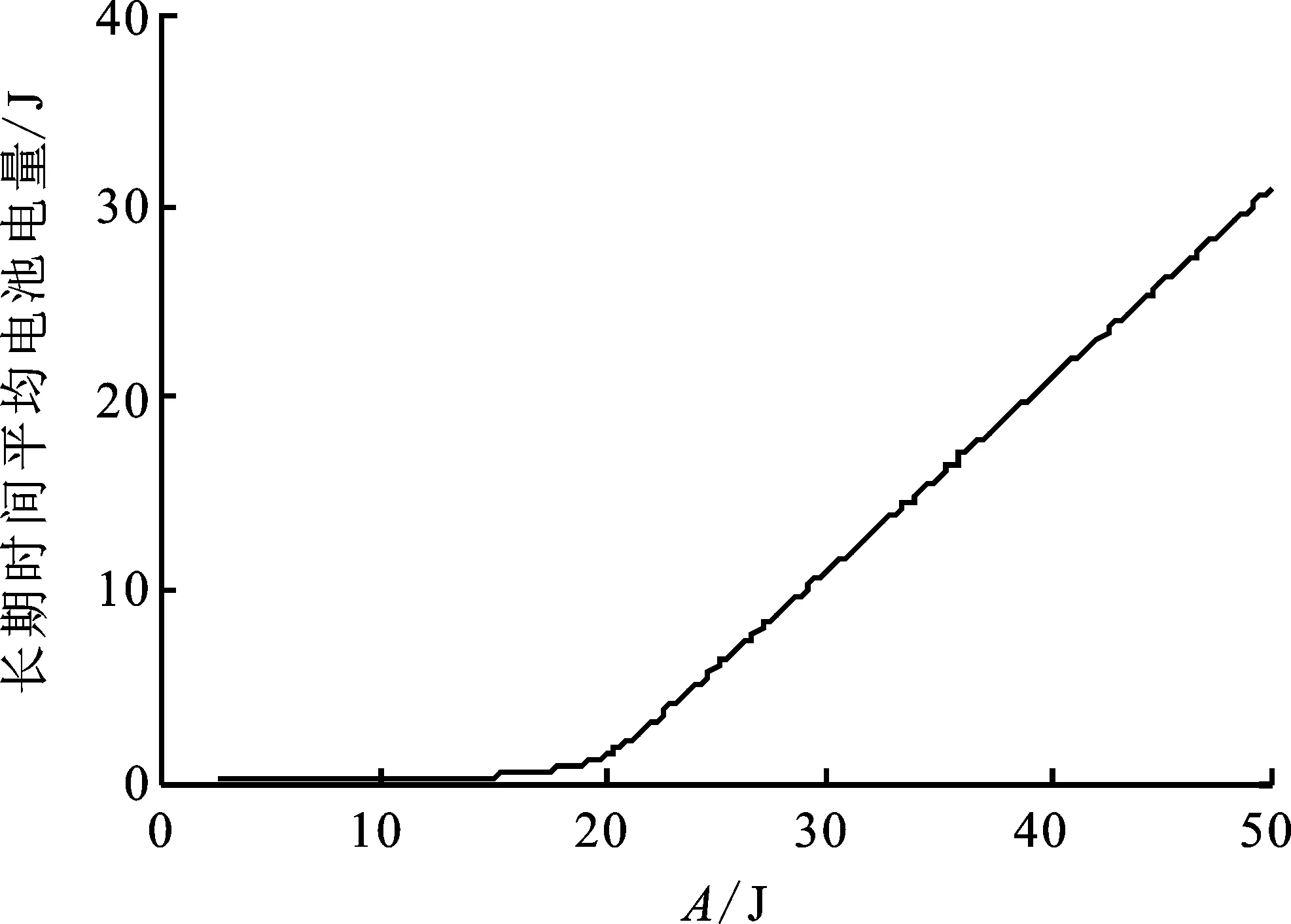
(a) 平均电池电量

图8给出了系统性能随能量达到率λ变化的情况，其中图8(a)为平均电量随能量达到率λ变化的情况，图8(b)是传输速率的变化情况。随着能量达到率λ的提高，电池平均每时隙收集的能量增多，能支持更高信号传输功率和更多同时激活的射频电路，因此能获得更高的传输速率。

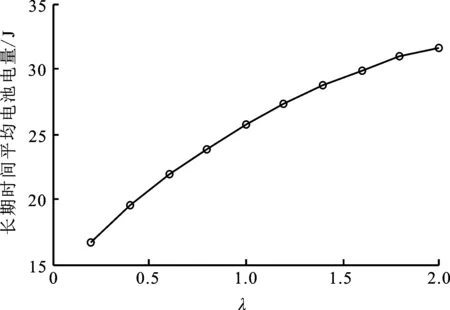
(a) 平均电池电量

4 结束语

对发送机由能量收集设备供电的点对点无线通信系统，以最大化长期传输速率为目标，对发送功率和发送天线选择进行联合优化。系统的功耗模型中，除信号的发送功率外，还包括了天线激活后射频电路的功耗，首先构造了可用能量和电池操作约束下的优化问题模型，然后利用李雅普诺夫优化框架将长期优化问题转换为电池电量虚队列要求下的速率最大化问题，进一步转换为单时隙的虚队列漂移加惩罚最小化问题。由于发送天线集合和发送功率联合优化问题不能直接求解，因此采用遍历可能天线数，分别优化不同天线数下的发送功率，然后选择使漂移加惩罚最小的天线数和发送功率作为最优解。仿真结果显示，相比贪婪、半贪婪算法以及天线数固定取值功率优化算法，笔者提出的算法能获得明显更高的传输速率。笔者提出的算法仅依赖于当前的电池状态和信道状态信息做出决策，计算复杂度低，是一种实用很强的算法。