基于NARNN方法的某隧道围岩变形预测

杜润泽， 姜志伟

（1.山东科技大学泰安校区资源学院，山东泰安266101；2.青岛理工大学土木工程学院，山东青岛266033）

0 引言

从隧道围岩变形现场监测数据可知［1-4］，由于岩体中存在大量的节理、裂隙等结构面，使得隧道开挖是一个复杂的非线性系统，其在力学行为上表现为随机性与确定性相结合的非线性特征，这些为精准预测预报岩体变形增加了难度。基于此，一些非线性预测模型［5-13］应用到围岩变形预测中，比如预测断层破碎带围岩变形的GA-BP神经网络综合预测模型，基于果蝇算法改进的广义回归神经网络预测模型，隧道沉降量预测的灰色GM（1，1）模型，研究围岩变形特征的R/S分析法和FA-NAR模型；或将神经网络预测模型与马尔科夫链结合，将小波函数引入BP神经网络的BP高阶小波神经网络算法等模型。回归分析模型利用已知确定的模型来表达各个变量之间的关系，但在外推的过程中会影响预测精度；时间序列模型本质上属于回归分析模型，在预测精度上也存在短板；灰色系统模型适合对变化规律的数据进行预测，长期预测数据变化不规律时依然会影响精度。

上述研究一定程度上解决了现场隧道围岩变形预测的非线性问题，但是在软弱围岩变形预测问题上还存在一些不足之处，同一工程案例，运用不同的预测方法，会得到不同的预测结果，某些数据不能真实的反映隧道实际情况。文中结合某软弱千枚岩隧道工程案例，以现场监测变形数据作为数据样本，通过设置训练样本、验证样本和测试样本，确定隧道围岩变形NARNN方法的延迟阶数和隐藏层神经元个数，以期对隧道围岩变形进行预测，使结果既满足工程预警时间需求，又保证预测精度要求，为确定二次衬砌施作的最佳时机提供依据。

1 工程概况

1.1 地质概况

四川灾后重建项目省道线五标段游坪隧道为单洞隧道，总长为1070m。设计隧道纵面位于-2.852%下坡段。隧道净宽9.0m，净高5.0m。隧址区为深切割构造侵蚀低山地貌，洞身地势较高，进出洞口地势较低、地势较陡，斜坡坡角30°～55°，局部受冲沟切割，下层的基岩为属变质岩的千枚岩，强风化带的岩芯较破碎，片理面极其发育，松散破碎且自稳能力差，围岩等级为Ⅳ级，土石类别为软石。

1.2 现场监测数据分析

提取隧道典型断面K9+700、K9+810拱顶沉降和洞周收敛的时程监测数据曲线，如图1所示。由图1可知，这两个断面围岩变形特点：

图1 围岩变形监测曲线

（1） 已监测得到的变形曲线可分为两阶段，一是在1～12d快速变形阶段，洞周收敛最大变形速率达到12.83mm/d，拱顶沉降最大变形速率可达9.32mm/d，这要是由于开挖卸荷初期围岩承载力较低造成的，此变形速率已达到预警级别；二是在13～25d缓慢变形阶段，这个阶段主要是由于初期支护结构强度提升，围岩和初期支护经过应力重分布形成共同受力体系，共同承受外部荷载，减缓了围岩变形。

（2） 从图1（a）变形曲线看，其具有非线性，虽然后期的变形均具有较强的趋势性，但是，不易从曲线自身发展趋势判断断面是否稳定；从图1（b）变形速率曲线看，其震荡明显，更是无法判断其趋势性，即无法判断断面变形是否稳定。

综上，从隧道围岩变形曲线和变形速率曲线很难研判围岩所处的这两个断面是否会发生失稳危险，需要采用其他方法进一步分析并给出预判。

2 围岩变形预测方法

2.1 NARNN方法

由于隧道围岩变形位移序列所表现出的非线性特点，故可利用神经网络非线性逼近原理对其进行预测，在已有的研究方法背景之下，提出了基于NARNN的非线性预测模型。NARNN的基础是非线性时序自回归模型，该模型是一种以自身作为回归变量，利用某段时间内随机变量的线性组合来描述该段时间后某时刻的随机变量，其主要由输入层、输入延迟层、隐含层和输出层组成。在NARNN中，延迟反馈为输出信号的时间延迟信号，是通过自回归将输出的延迟信号作为网络输入，再利用隐含层和输出层的运算得出网络输出，对于时间序列{xt}，t=1，2，3，…，n，其模型可表示：

式中，e（t）为x（t）的扰动项，是随机白噪声，且和前一时刻序列x（t）不相关。通过式（1）可以看出，当前时刻x（t）是取决于x（t-1）、x（t-2）、…x（t-n）的值，这样的模型称为n阶自回归模型，其表示当前时刻的数据与之前数据的关联程度。采用的NARNN可以表示：

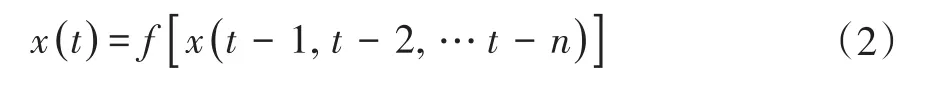
对于只知道过去位移值的隧道围岩变形问题而言，在建立模型过程中把历史值看作包含隧道围岩特性的当前有效值，直接建立当前位移同过去各位移历史值间的神经网络模型，对岩土工程问题比较适宜，其网络信号构造如图2和图3所示。

图2 NARNN网络信号构造图

图3 NARNN结构图

输入信号为xi，隐含层中，模型通过激活函数g和权值wij以及隐含层阈值aj可计算出隐含层各神经元的输出vj，计算公式：

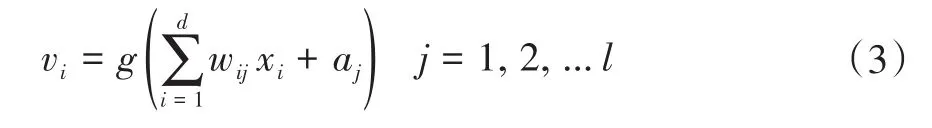
式中，d为输入延迟阶数，l为隐含层神经元数目，g为隐含层的激活函数；xi为第i个输入数据，wij为第i个输出时间延迟信号和隐含层第j个神经元之间的连接权值；aj为第j个隐藏层神经元阈值。输出层根据隐含层的输出vj，计算出网络模型的输出y，计算公式：

式中，wj为隐藏层第j个神经元与输出层神经元之间的连接权值，b为输出层神经元阈值。

通过网络模型构造可以看出，每一次的输出信号y时间延迟后，作为该网络中时间延迟反馈，输入到隐含层中，作为下一次y输出的调整参数，经过隐含层与输出层的计算求得网络输出，并循环该过程，以此提高预测精度。该模型对于呈不平稳时间序列数据，特别是存在着存在不从一个相对平稳区突变到另一个相对平稳区，即存在数据震荡现象时，通过调节权重，可以自动寻找满足误差精度的参数，因此，NARNN模型可以反映系统的历史状态，具有很强的记忆功能，可应用到非线性时间序列的预测中。

2.2 围岩变形NARNN方法分析流程

围岩变形NARNN方法分析流程如图4所示。

图4 NARNN分析方法流程图

具体步骤如下：

（1） 将隧道围岩变形监测数据导入MATLAB作为数据样本，对变形位移数据和变形速率数据分别进行设置训练。对数据样本进行配置，为了保持预测的准确性，分别设置训练样本、验证样本和测试样本，训练的目的是为了寻找当前数据与之前数据的相关关系，建立一个能完整反映这种相关关系的网络。

（2） 设置延迟阶数和隐藏层神经元个数，由于模型的预测值是由前一组样本所决定的，可以根据样本的自相关系数ACF值来确定NARNN模型的延迟阶数。一般认为神经网络的隐含层神经元个数与输出单元有关，隐含层神经元个数的确定采用经验式（5）和式（6）：

式中，n为输入单元数；m为输出单元个数，a为常数，取经验值1～10。训练方法采用Levenberg Marquardt算法对NARNN模型进行训练。根据隧道围岩变形监测样本建立NARNN通过训练的延迟反馈调整延迟层和隐含层参数，当NARNN模型的均方误差达到最小值时，则可确定此条件下延迟层阶数和隐含层神经元个数为该模型的最优神经元参数，均方根误差计算公式：

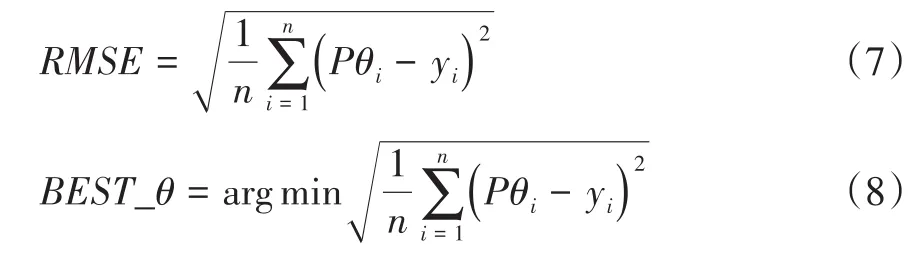
式中，Pθi为在θ组参数情况下神经网络的输出值；yi为真实值；n为输出值的长度；BEST_θ为所有参数组合中RMSE最小情况下的参数。

（3） 若通过误差分析验证NARNN模型不满足要求，则继续进行第二步的网络操作。

（4） 训练结束后，检测模型误差的自相关性，以确定模型的适用性。NARNN方法认为模型误差的自相关系数在95%置信区间范围内时，模型误差的自相关系数近似为0，即误差之间不存在相关性，认为模型构建效果较好。当NARNN训练满足要求后，再进行NARNN预测，获取围岩变形预测数据。

2.3 NARNN围岩变形预测

结合图1所示的监测数据，通过网络试验，将隧道围岩变形和变形速率数据样本按照如下设置，其中训练样本（70%）、验证样本（15%）和测试样本（15%），计算围岩变形时序在不同神经元参数下的均方误差，待均方误差最小且误差自相关性良好时，可确定模型的最优神经元参数，各围岩变形时序的最优神经元参数见表1。

表1 NARNN模型最优神经元参数

图5为得到的拟合误差曲线，拟合误差数值见表2。由表2中的误差数据可知，预测输出最大误差绝对值和均方误差都很小，说明NARNN神经网络对围岩变形时序具有良好的拟合预测效果。

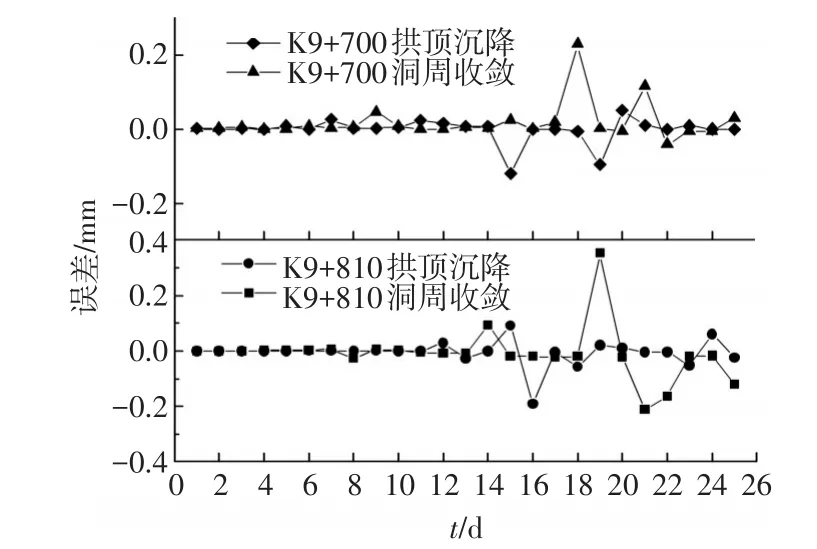
图5 拟合误差曲线

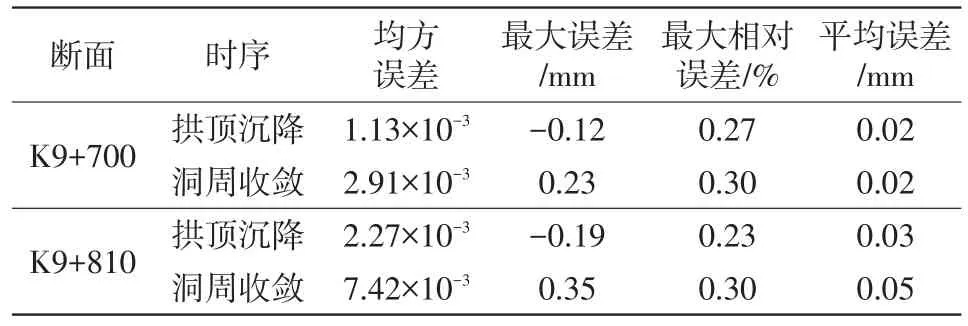
表2 拟合误差表

采用此时相关参数，预测第26～30d的围岩变形，预测数据见表3、表4，曲线如图6所示。由图6可知，断面K9+810围岩变形仍然会呈增加趋势，而变形速率总体呈减小趋势，变形速率基本稳定在1mm/d以内，可判定围岩变形正趋于稳定；而断面K9+700围岩变形也呈增加趋势，且变形速率在不断增大，在30d时，变形速率已增加到10mm/d左右，需要及时进行治理，实地观测发现该里程在其后的几天时间发生较大变形和岩土体松散剥落。因此，该预测方法能够较好反映当前软岩公路隧道开挖支护过程中的实际围岩变形状况。

表3 断面K9+700变形预测数据

表4 断面K9+810变形预测数据

图6 监测、预测数据曲线

3 结语

（1） NARNN模型对软弱隧道实例的验证，所得到的的拱顶沉降和洞周收敛值均满足要求，说明NARNN模型适用于该案例中的软岩隧道的变形预测问题。

（2） 将现场监测数据作为数据样本，建议按照训练样本（70%）、验证样本（15%）和测试样本（15%）分配设置，可以获得较好的延迟阶数和隐藏层神经元个数，既减少了人为输入网络参数的盲目性，又提高了网络的学习能力和预测精度。

（3） 围岩松散破碎风化严重的千枚岩隧道围岩变形期持续时间较长，通过NARNN模型的出的预测数据可知，在进入稳定变形阶段应及时施作二次衬砌，以控制围岩继续变形，避免因初期支护破坏而导致工程事故发生。