考虑运动加速度干扰的无人机姿态估计算法

刘旭航，刘小雄，章卫国，杨 跃，郭一聪

(西北工业大学 自动化学院，西安 710072)

低成本无人机导航系统主要由基于微机电系统(Micro-electromechanical system,MEMS)的传感器组成，局限于成本和功耗，噪声误差和偏移误差导致陀螺仪的精度下降[1-2]，仅利用陀螺仪不能实现准确的姿态估计，互补滤波被用来融合陀螺仪、加速度计和磁力计信息，获得稳定的姿态。近年来随着传感器技术的飞速发展，基于互补滤波的姿态估计算法在无人系统中得到了广泛的应用[3-5]。

传统的互补滤波模型采用加速度计和陀螺仪作为辅助传感器，利用陀螺仪和辅助传感器的噪声频段互补的特性，减小噪声信号对姿态估计的干扰，但是在动态环境下，载体具有较大的运动加速度，运动加速度对姿态估计的结果产生严重干扰，针对上述问题，国内外研究人员提出了不同的姿态估计算法。李瑞涵等[6]提出一种加速梯度姿态融合方法，利用阈值切换的方法来抑制运动加速度的干扰，该算法抑制运动加速度干扰的能力优于传统的互补滤波算法，但并没有给出运动加速度准确值。Euston等[7]计算向心加速度作为运动加速度，排除运动加速度对姿态估计的干扰，但是该方法未考虑切向加速度，对运动加速度的估计仍不够精确。匡敏驰[8]设计了一种新型的垂直/水平欧拉角姿态解算方法，利用惯性器件、磁力计、全球定位系统(Global positioning system, GPS)和空速计的不同特性，获得准确的姿态信息。但是该算法中运动加速度由更新频率较低的GPS和空速计求得，系统误差不能及时得到修正，姿态估计的精度不高。王鼎杰等[9]采用惯性导航系统(Inertial navigation system, INS)和GPS构建组合导航系统，通过扩展卡尔曼滤波(Extended Kalman filter, EKF)算法获得实时的姿态信息和位置信息。但是该算法需要高精度且稳定的量测信息，通常采用定位精度达到厘米级的差分GPS，但差分GPS体积大，且价格昂贵，不适合在低成本无人机导航系统中使用，单点GPS成本低，但精度较低，更新频率较慢，在使用单点GPS的导航系统中，采用经典的GPS/INS组合导航算法获得的姿态角依然存在较大误差。Lee等[10]设计了一种将姿态角和运动加速度联合估计的姿态估计算法，运动加速度被建模成一阶低通白噪声过程，能够在短加速周期内精确估计运动加速度，但是涉及数值较大的外部加速度时，该算法不能实现对运动加速度的准确估计。

现有的无人机姿态估计算法存在精度低，无法精确估计运动加速度的缺点，为解决动态环境下低成本无人机姿态估计易受传感器噪声和运动加速度干扰的问题，本文设计了一种考虑运动加速度干扰的姿态估计算法。首先，建立运动加速度估计模型，该模型分别从加速度计和GPS速度中求取运动加速度，利用获得的运动加速度对加速度计原始值进行修正，从而排除运动加速度对姿态估计的干扰。然后，建立基于互补滤波的姿态估计模型，利用修正后的加速度信息和磁力计信息作为参考向量，构建误差量作为互补滤波器的输入，互补滤波器的输出为修正后的陀螺仪角速度，通过基于互补滤波的姿态估计模型抑制传感器噪声干扰，提升姿态估计的精度。最后，利用无人机试飞过程中采集的传感器数据，设计对比实验验证本文所设计算法的有效性。

1 运动加速度估计模型

1.1 模型框架

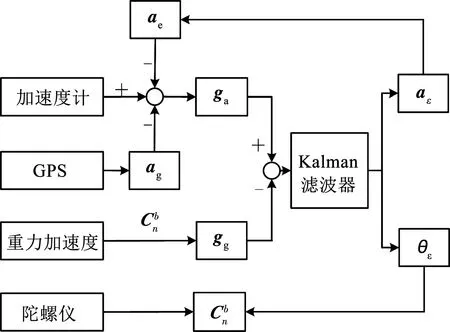
图1 运动加速度估计模型框架Fig.1 Framework of motion acceleration estimation model

由于卡尔曼滤波器只能在短时间精确估计运动加速度ae，误差的累积导致ae的精度逐渐下降。因此，引入外部运动加速度ag，ag由GPS速度信息差分获得，ag的数值较为稳定，但是由于外部传感器GPS的更新频率远低于导航系统姿态更新的频率，单独使用外部传感器估计运动加速度会导致姿态估计的精度下降。因此，在运动加速度估计模型中，同时利用ae和ag对加速度计原始值进行修正，提升姿态估计的精度和抗干扰能力。

1.2 误差运动加速度

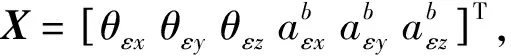
Xk=Fk,k-1Xk-1+wk

(1)

式中：Fk,k-1为状态转移矩阵，wk为噪声分量。

(2)

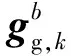
(3)

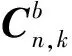
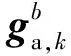
(4)

式中，ΔR( )为旋转角度为θε,k旋转矩阵。

由式(4)，系统量测方程为

(5)

由于滤波后得到运动加速度误差aε和姿态角误差θε分别对运动加速度和姿态角进行了修正，修正后的误差量为零，因此，相邻时刻的状态变量不相关，更新后的状态一步预测等于零，状态一步预测方程简化为

(6)

状态估计方程简化为

(7)

滤波增益为

(8)

一步预测均方误差为

Pk/k-1=Φk,k-1Pk-1Φk,k-1+Qk=Qk

(9)

估计均方误差为

Pk=(I-KkHk)Pk/k-1

(10)

(11)

1.3 外部运动加速度

在低成本无人机导航系统中，GPS更新周期慢于加速度计更新周期，设加速度计更新周期为T1,GPS更新周期为T2，T1和T2通常存在倍数关系，即T2=nT1，其中，n为正整数。

(12)

(13)

式中，dt为加速度更新周期T1。

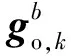
(14)

(15)

2 基于互补滤波的姿态估计

由于陀螺仪噪声主要存在于低频段，加速度计和磁力计噪声主要在高频段，因此，设计互补滤波器滤除噪声的干扰。设陀螺仪输出值为ωg，由修正加速度和磁力计得到的角速度修正值为ωc，载体角速度真实值为ω，则有如下关系:

(16)

式中：ng为陀螺仪低频噪声，nc为加速度计和磁力计的高频噪声。在互补滤波器中，对ωg应用高通滤波器H，对ωc应用低通滤波器L，即

ω=L×ωc+H×ωg=
(L+H)×ω+L×nc+H×ng

(17)

由低通滤波器和高通滤波器性质，有如下关系:

(18)

滤波后的角速度为

ω=(L+H)×ω

(19)

低通滤波和高通滤波的传递函数如下所示[13]：

(20)

(21)

L(s)与H(s)的和为1，说明经过滤波后的角速度与真实角速度相同，且不包含传感器噪声。

由于角速度修正值ωc来自修正加速度和磁力计，含有高频噪声，因此控制器一般不应含有微分项，通常采用如下形式比例积分(Proportional-integral, PI)控制器：

(22)

式中，KP、KI分别为比例和微分系数，其选值受传感器参数和载体运动状况的影响[14]。

基于互补滤波的姿态估计算法采用来自修正加速度和磁力计的信息构建误差量，并将该误差量作为PI控制器的输入，PI控制器的输出为角速度修正值ωc，ωc被用来消除由陀螺仪漂移和偏差带来的累积误差，姿态角由修正后的角速度通过方向余弦法解算。基于互补滤波的姿态估计算法的框架如图2所示。

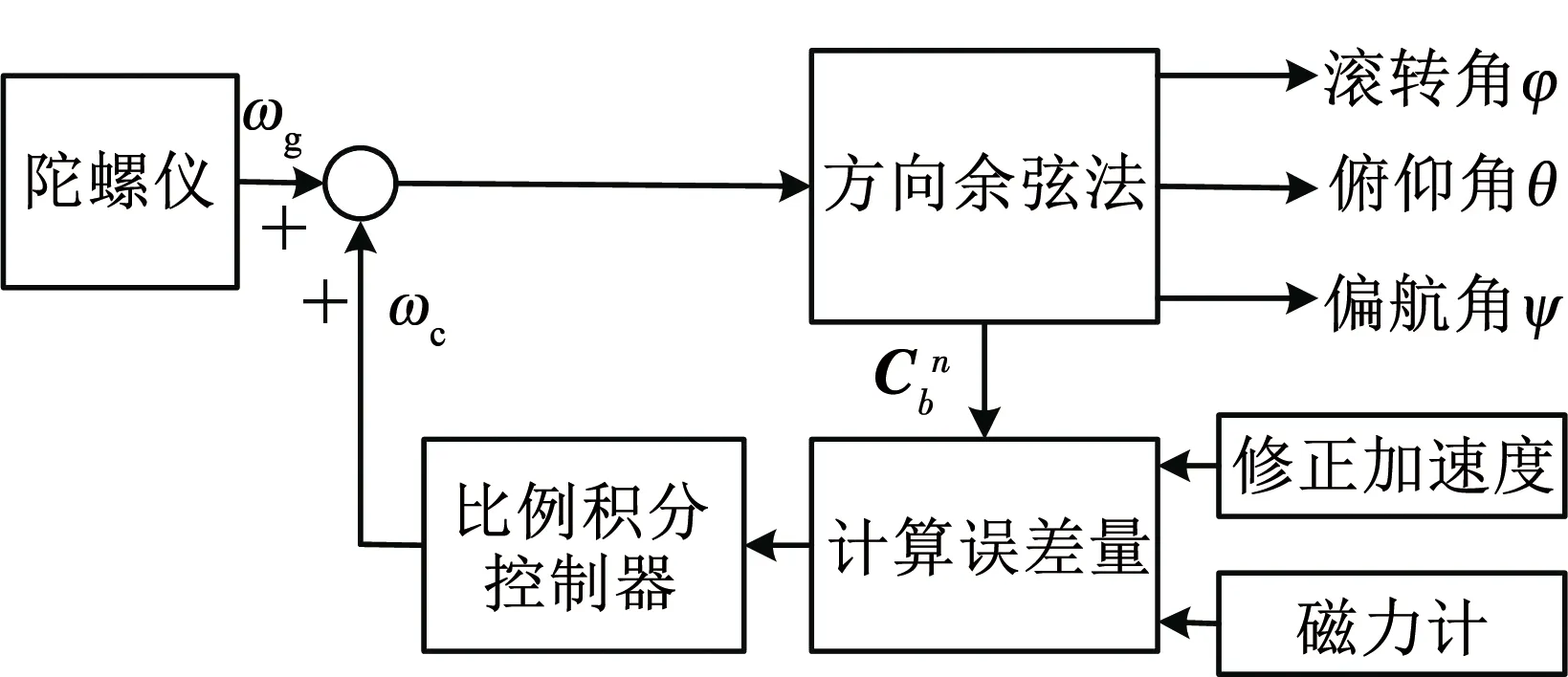
图2 姿态估计算法框架图Fig.2 Block diagram of attitude estimation algorithm

2.1 方向余弦法

方向余弦矩阵的微分方程为

(23)

其中

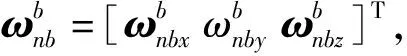
由式(23)，当时间间隔dt趋向于无穷小时，方向余弦矩阵更新可以表达为如下形式:

(24)

式(24)利用陀螺信号实现了方向余弦矩阵的实时更新，利用方向余弦矩阵可以求出姿态角，姿态角与方向余弦矩阵的关系如下所示:

(25)

2.2 误差量的计算

采用参考向量和观测向量做外积的方式计算误差量，误差量由修正俯仰角和滚转角的误差量e1和修正偏航角的误差量e2组成。

(26)

单位化的修正加速度g2为与参考向量g1相同大小和方向的另一向量，利用运动加速度估计模型计算修正加速度gb，在GPS信号未更新的时刻，gb为由误差运动加速度修正得到，GPS信号更新的时刻，gb由外部运动加速度修正得到，即

(27)

对修正加速度单位化处理:

(28)

g2与参考向量g1做叉乘，求出误差向量e1。

e1=g1×g2

(29)

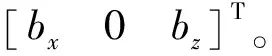
(30)

在n系的XOZ平面上和Z轴上，磁力计测量值应为同一组模值[15]，即

(31)

(32)

误差量e2由参考向量m1和磁力计输出值m2叉乘获得:

e2=m1×m2

(33)

总的误差量为e1与e2的和:

e=e1+e2

(34)

2.3 PI控制器

误差量e为PI控制器的输入，PI控制器的输出量存在ωP和ωI两个分量，分别为：

ωP=KPe

(35)

ωI=ωI+KIe·dt

(36)

式中dt为方向余弦矩阵更新的周期。

综上所述，由修正加速度和磁力计得到的角速度修正值ωc为

ωc=ωP+ωI

(37)

3 实 验

3.1 传感器数据采集

进行无人机飞行试验，利用搭载于固定翼无人机的Ellipse2-N系统采集所需要的传感器信息，Ellipse2-N系统(如图3所示)包含了基于MEMS的惯性测量单元和GPS接收机，惯性测量单元中集成了陀螺仪、加速度计和磁力计。表1为Ellipse2-N系统的参数特性。

图3 Ellipse2-N惯性导航系统Fig.3 Ellipse2-N inertial navigation system

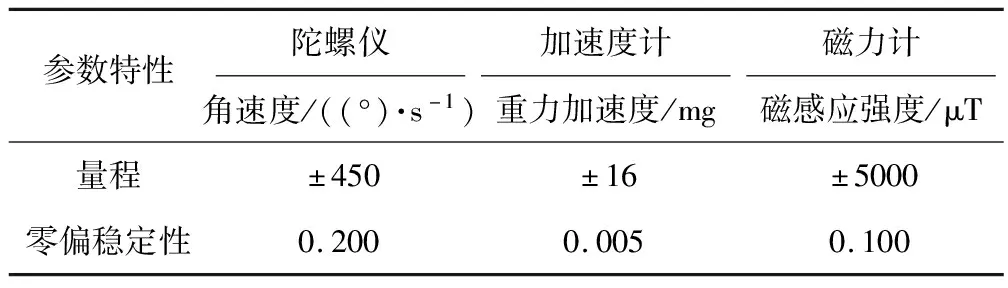
表1 Ellipse2-N参数特性Tab.1 Parameter characteristics of Ellipse2-N

利用Ellipse2-N系统采集陀螺仪、加速度计、磁力计和GPS速度信息。参考姿态为Ellipse2-N系统输出的姿态，其滚转角和俯仰角的误差均方根均小于0.1°，偏航角的误差均方根小于0.5°。GPS接收机的速度更新频率为10 Hz，精度为0.1 m/s。采集时长为80 s的实验数据，初始滚转角为-23.60°，俯仰角为0.8°，偏航角为-80.6°。陀螺仪、加速度计和磁力计的采集频率均为50 Hz，GPS速度的采集频率为10 Hz，无人机在该段时间内盘旋飞行。

3.2 运动加速度估计模型的验证

首先利用时长为3 s的传感器数据进行仿真实验，验证运动加速度估计模型的估计效果。ga为加速度计输出值的模值，go是仅使用外部运动加速度修正后的得到的加速度的模值，ge为仅使用误差运动加速度修正后得到的加速度的模值，gp为使用运动加速度估计模型获得的加速度的模值。gl为当地重力加速度的模值。图4为加速度模值的对比图，表2为由不同算法得到的加速度模值的统计特性。

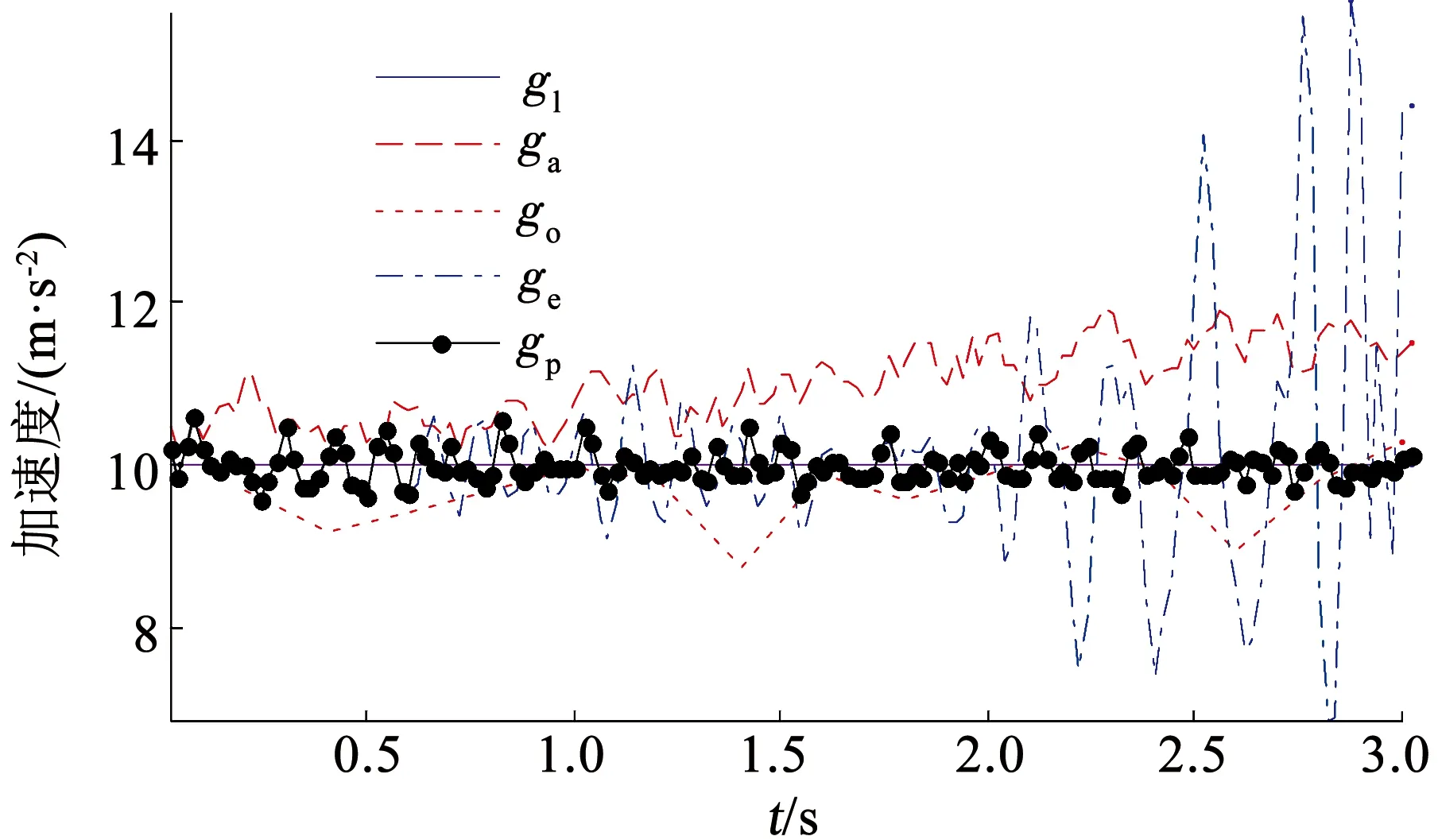
图4 加速度模值对比图Fig.4 Comparison of acceleration modulus

表2 加速度模值的统计特性对比Tab.2 Comparison of characteristics of acceleration modulus(m·s-2)

观察图4，加速度计输出值的模值ga变化区间为[10.2,11.9]，大于当地重力加速度gl，说明载体在该段时间内具有运动加速度。由于GPS更新周期较长，go数值跳变剧烈且更新频率较慢，ge在前1 s内数值接近gp，随后ge偏离gl的程度迅速加大，这是由于误差运动加速度仅能在短时间内准确估计运动加速度，gp数值偏离gl的程度最小。

采用平均绝对误差(Mean absolute error, MAE)和均方根误差(Root mean squared error, RMSE)来衡量观测值同真值之间的偏差，观察表2，gp所对应的的MAE值和RMSE值最小。

综上所述，利用运动加速度估计模型对加速度计原始值修正后得到的修正加速度最接近真实的重力加速度，运动加速度估计模型对载体运动加速度估计的精度最高，可以有效抑制动态环境下运动加速度对加速度计测量值的干扰。

3.3 考虑运动加速度的姿态估计算法验证

利用时长为80 s的传感器数据对所设计的考虑运动加速度干扰的姿态估计算法进行验证。参考姿态角来源于Ellipse2-N惯性导航系统，记为RE，本文所设计算法得到的姿态角记为PR。图5为加速度计输出模值，图6为姿态角对比图。

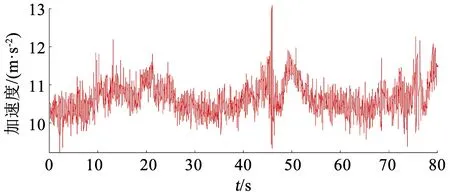
图5 加速度计输出模值Fig.5 Output modulus of accelerometer

图6 姿态角对比图Fig.6 Comparison of attitude angle

图5中加速度计输出模值变化区间在[9.3, 12.9]，表明载体具有运动加速度。由图6可知，本文所设计的算法估计得到的滚转角和俯仰角与参考值之间的误差均小于1°，偏航角与参考值之间的误差小于2°。因此，在具有运动加速度干扰的高动态环境下，本文所设计的姿态估计算法能够给出稳定可靠的姿态。

3.4 不同姿态估计算法的性能比较

分别采用不考虑运动加速度的互补滤波姿态估计算法和基于EKF的GPS/INS组合导航算法，以及本文所设计的算法，同时处理时长为50 s的传感器数据，将不考虑运动加速度的互补滤波姿态估计算法的估计值记为CF，GPS/INS组合导航算法的估计值记为EKF，考虑运动加速度的姿态估计算法的估计值记为PR。图7为加速度计输出模值，图8为姿态角误差对比图所示，表3为3种算法的误差统计特性。

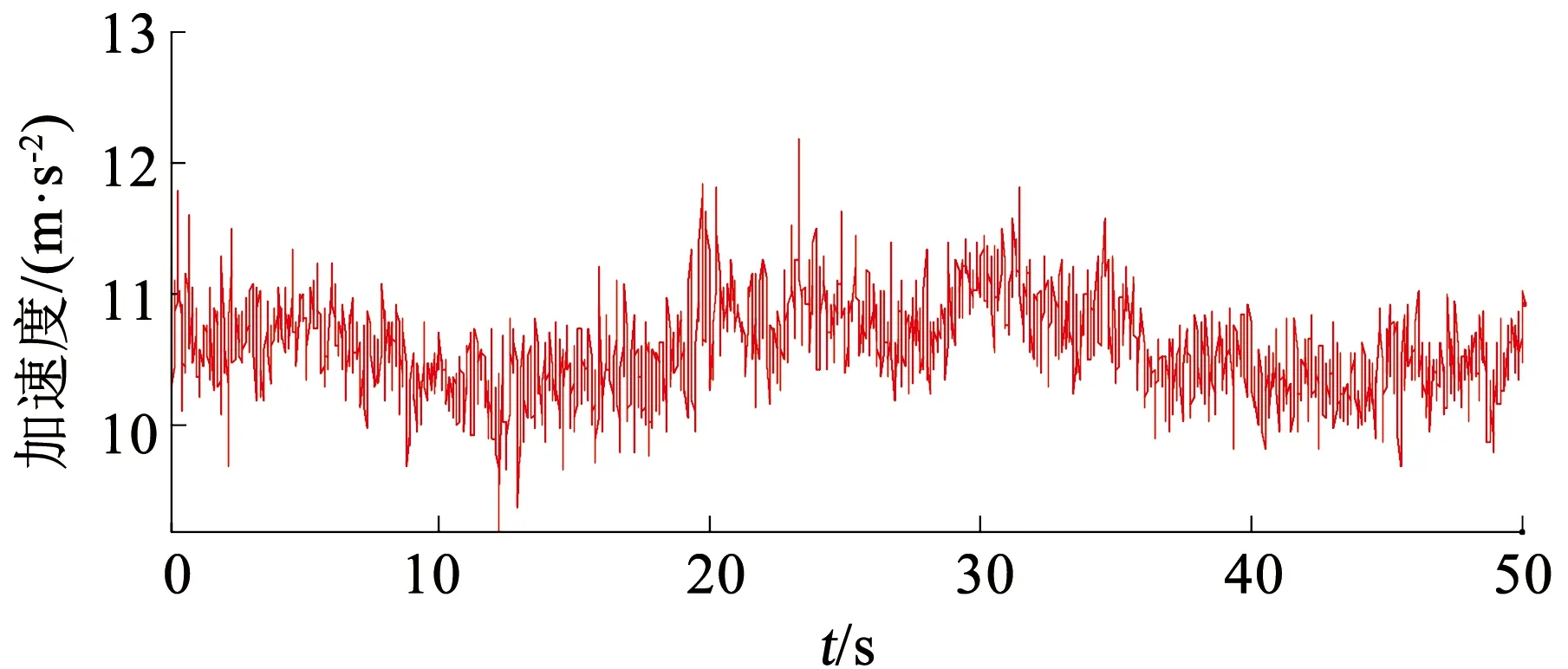
图7 加速度计输出模值Fig.7 Output modulus of accelerometer

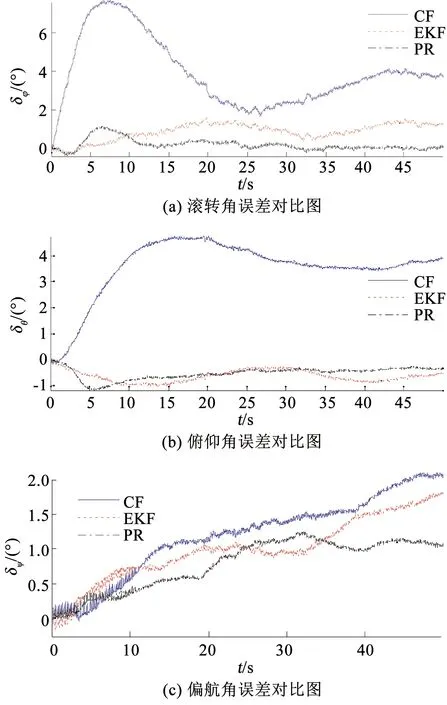
图8 姿态角误差对比图Fig.8 Comparison of attitude angle error

图7中加速度计输出模值变化区间为[9.3，12.2]，即载体在该段时间内具有运动加速度。由图8可知，在存在运动加速度干扰的情况下，考虑运动加速度的姿态估计算法的俯仰角和滚转角的误差值均小于1.2°，偏航角误差值小于1.3°。原始的互补滤波算法由于运动加速度的干扰，俯仰角误差和滚转角误差分别达到7.6°和4.8°。偏航角误差达2.1°，且呈发散趋势。基于EKF的组合导航算法受限于单点GPS速度的较差的性能，其俯仰角误差值和滚转角误差值与本文所提出算法的对应的误差值类似，但偏航角误差值大于1.6°，远大于本文所提出算法的偏航角误差值。

进一步观察表3中不同算法的姿态角误差的统计特性，本文所设计算法姿态估计的平方绝对误差和均方根误差均小原始互补滤波算法和基于EKF组合导航算法所对应的平方绝对误差和均方根误差，即本文所设计算法姿态估计的性能优于原始互补滤波算法和基于EKF的组合导航算法，该算法能够有效提升无人机导航系统在动态环境下姿态估计的精度。

表3 姿态角误差的统计特性对比Tab.3 Comparison of characteristics of attitude angle error (°)

4 结 论

1)动态环境下，无人机机动所产生的运动加速度和低成本传感器固有的噪声对导航系统姿态估计存在严重的干扰，针对这一问题提出了一种考虑运动加速度干扰的姿态估计算法。

2)该算法首先利用运动加速度估计模型精确估计运动加速度，避免运动加速度对姿态估计的干扰。然后构建基于互补滤波的姿态估计模型，进一步减小陀螺仪的噪声信号对姿态估计的干扰，实现准确的姿态输出。

3)实验结果表明，所提出算法能够准确估计无人机运动加速度，减弱运动加速度和传感器噪声对姿态估计的干扰，该算法在提高低成本无人机导航系统姿态估计的精度和抗干扰能力方面具有较高的实用价值。