基于散射体信息的室内NLOS单基站定位算法
王 亚,田增山,李 泽,李 升
(重庆邮电大学 通信与信息工程学院,重庆 400065)
0 引 言
现代生活正朝着智能化方向发展,许多应用例如自动驾驶、虚拟现实、消防人员定位、购物商场客人位置、医院病人及监狱罪犯活动范围等,都需要获取目标的位置信息[1]。由于室内复杂的建筑结构,无线信号的非视距(non-line-of-sight,NLOS)传播普遍存在[2],而现有的基于视距信号(line-of-sight,LOS)的定位算法很难应用在室内NLOS环境中。因此,研究室内NLOS环境下的定位技术具有重要意义。
现有的室内定位技术可分为2类:①基于无线信号的定位技术,例如蓝牙定位技术[3]、WiFi[4]、超宽带(ultra wide band,UWB)[5-6]等;②基于传感器的定位技术,例如惯性导航技术等。随着无线技术的发展,现有的无线定位技术多采用到达时间(time of arrival,TOA)或飞行时间(time of flight,TOF)[7-8]。然而,由于多径效应及NLOS传播[9],定位精度一般较差。为解决NLOS下的定位问题,文献[10]提出了一种抑制NLOS定位误差方法,该方法通过分组将位置之间的差值作为定位残差,对临时迭代出的目标位置的残差次方进行加权进而减弱误差,在NLOS误差抑制方面做出很大突破。为了提高NLOS环境下的定位精度,文献[11]基于UWB信号的到达时间差(time difference of arrival,TDOA)进行定位建模,然后通过粒子群优化算法求出最优解[12]。
现有的NLOS误差抑制算法中普遍需要多个基站,而多站之间的同步需要付出一定代价,因此,使用单个基站定位具有更现实的意义[13],但在NLOS环境下,使用单个基站定位更具有挑战性。最近出现一些新的定位方法区别以往的抑制多径算法,其采取化“敌人”为“朋友”的新思路,进而将NLOS路径作为有利条件对目标进行定位。文献[14]提出多径三角定位的概念,只借助单个基站,利用直射路径和反射路径构建三角定位模型,从而实现分米级精度的WiFi定位系统。类似地,文献[15]利用直达路径和反射路径的相对TOF、到达角(angle of arrival,AOA)、离开角(angle of departure,AOD)实现单基站下的高精度定位,然而该系统利用跳频技术,使得所提方法无法在现有网络当中使用。此外,一些算法对室内存在的反射物体进行了反射系数、反射强度及材料特性的研究,为利用散射体进行定位创造了条件[16]。文献[17]利用反射镜像分析法,结合信号的空间传播模型与建筑几何平面图等先验信息,提高了多径传播条件下的定位精度。另外,由于现有网络中存在相位误差,例如载波频偏(carrier frequency offset,CFO)和误差采样定时偏移(sampling timing offset,STO)[18],因此,利用绝对的TOF进行单基站定位比较困难,利用多径信号之间的相对关系将此类误差相互抵消将是一个很好的研究内容。
本文提出一种在NLOS环境下的单个基站定位算法。首先,根据室内建筑结构的先验信息,获得散射体的分布范围;其次,根据反射路径的AOA与散射体的分布范围进一步缩小散射体的分布范围;然后,利用搜索到的散射体位置及路径的TOF构建差分TOF最小化目标定位方程;最后,利用遗传算法(genetic algorithm,GA)对目标进行初步定位,使用列文伯格-马夸尔特(Levenberg-Marquard,LM)算法[19]对目标进行精确定位。
1 信道模型
室内环境中,信号在收发端之间传播的信道频率响应(channel frequency response,CFR)可以表示为[20]
(1)
(1)式中:γl和τl分别表示第l条路径的幅度和TOF;L为路径的个数;f为载波中心频率。本文采用路径的AOA及室内结构的先验信息来确定散射体位置,因此,基站需要使用多天线,线性阵列如图1所示。对于多天线而言,信道模型应变为多天线的矩阵形式,然后采用超分辨参数估计算法对AOA及TOF进行估计。在实际网络中,由于收发两端不同步会引入相位误差,主要包含CFO和STO,对于同一接收端的多径信号而言,可以通过差分的方法消除相位误差的影响,进而可以利用差分TOF对目标进行定位。
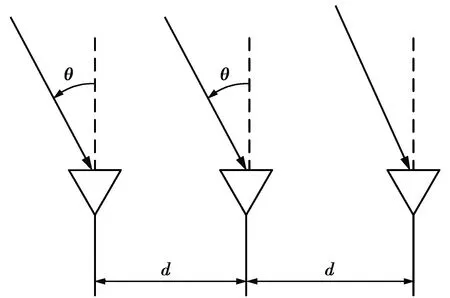
图1 阵列天线示意图Fig.1 Schematic of array antenna
2 室内NLOS单基站定位算法模型
本文提出的室内NLOS单基站定位的系统框图如图2所示,主要包括3部分:①利用室内场景布局的先验信息约束散射体的可行域;②利用AOA确定散射体的位置以及TOF构建差分定位方程;③提出一种GA、LM结合的目标位置求解定位算法。

图2 本文系统框图Fig.2 System block diagram of this paper
2.1 散射体可行域的建立规则
在室内NLOS环境下,单个基站的位置表示为p=(xb,yb),目标位置表示为u=(x,y),其与基站分别位于由一面墙壁隔开的2个房间内,墙的2个端点分别表示为Q1=(xd1,yd1)、Q2=(xd2,yd2),房间的长和宽分别为Le和We,定位示意图如图3所示。
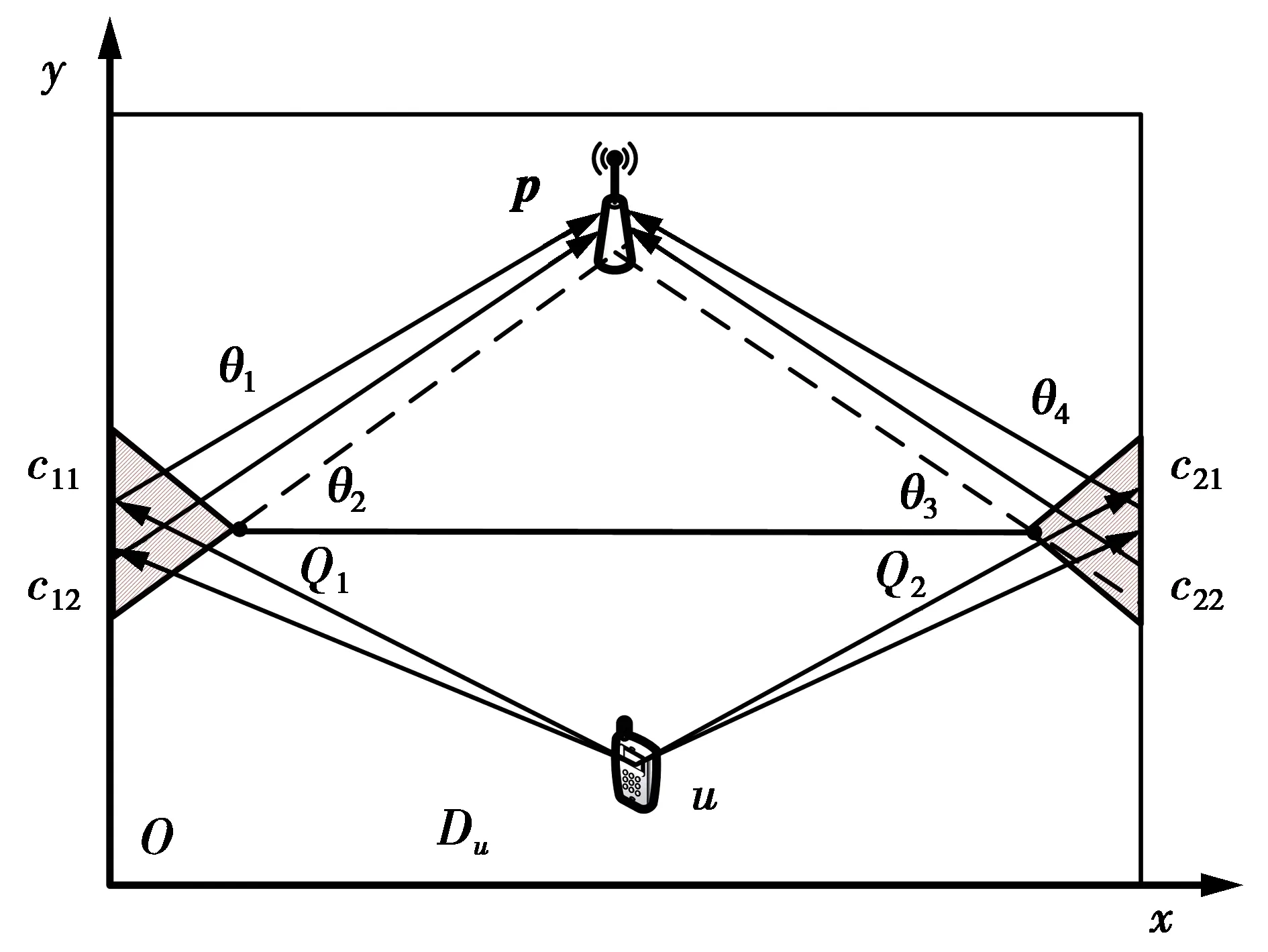
图3 室内NLOS单基站定位示意图Fig.3 Schematic diagram of indoor NLOS single base station location
假设墙壁的阻挡将LOS路径完全衰减,发射端的信号经由左右两侧到达接收端,因此,可将反射体的位置约束在两侧。根据射线传播原理,由基站及墙体位置可确定散射体的下边界点,将下边界的对称线作为上边界,这样可以缩小散射体的分布范围。可行域上边界点记为c11=(xc11,yc11),下边界点记为c12=(xc12,yc12);同理,右侧散射体边界点分别为c21=(xc21,yc21)、c22=(xc22,yc22)。左侧散射体分布区域表示为
(2)
(2)式中,l11和l12分别表示上下边界直线方程。同理,右侧反射体可行域表示为
(3)
(3)式中:l21和l22分别为右侧散射体区域上下边界直线方程;s=(xs,ys)为散射体坐标。
2.2 散射体可行域的缩小方法
为了进一步减小散射体的搜索空间,可以利用路径的AOA和散射体区的边界线来限定散射体的搜索范围。根据反射路径的AOA,基站与经过的散射体两点之间确定的直线l表示为
y-yp=tanθk(x-xp)
(4)
(4)式中:θk为第k条路径的AOA;k=1,2,…K,K为左右两侧的总路径数。
利用(4)式进行如下步骤。
步骤1当tanθk>0时,求解(4)式与直线x=0的交点E=(xe,ye),当ye
步骤2当tanθk<0,直线与右侧散射区域相交,则求解(4)式与直线x=Le的交点E=(xe,ye),当ye
步骤3当tanθk=0时,舍弃当前路径。
对于保留的路径,联合其所在的直线与散射体区域,可将散射体的位置进一步约束到可行域中的粗估计线段,表示为
Θ=l∩gi
(5)
然后,在粗估计线段上分别选取一定数量的散射体进行定位,散射体的数量与定位精度及运算时间有关。
2.3 单基站的NLOS区域确定
当目标位于区域Du时,即在基站NLOS传播范围内,单基站将获取不到直射路径,只能通过散射体反射构成的NLOS路径进行定位。区域Du可由基站和墙壁两端点所在的直线确定,表示为
(6)
当目标位于Du区域时,基站即可检测到经由反射区反射的路径,根据接收到的NLOS路径的AOA和TOF对目标位置进行估计。
3 目标定位方程的建立
为消除相位误差,选定一条反射路径的TOF作为参考,其他路径的TOF与其做差分构造差分TOF观测值,进而利用差分TOF构造非线性目标定位方程。具体地,定位参数估计值往往存在误差,因此反射路径的TOF表示为
(7)
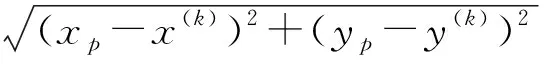
一般地,选第1条路径的TOF作为参考,表示为
(8)
第k条路径相对于参考路径的差分TOF可表示为
(9)
(9)式中,k=2,3,…,K。从(9)式可以看出,通过差分可以消除相位误差的影响。理论上,第k条路径相对于参考路径的差分TOF可以表示为
Δτk,1=τk-τ1=
(10)
Δτ+ε
(11)
(11)式中,ε为差分TOF的误差估计矢量,表示为
ε=[ε2/1,ε3/1,…,εK/1]T
(12)
Δτk,1为Δτ中第k个元素,理论上第k条路径相对于参考路径的差分TOF矢量表示为
(13)
(13)式中,i、j、m表示对应路径在散射区域选取的散射体索引。将对目标位置的估计问题转化为最小二乘的优化求解问题,表示为
(14)
(13)式中,散射体的位置是根据散射区域集合,即(5)式来选取的,这相对于整个室内空间,散射体的位置不确定性已经降低很多,从(14)式可以看出,散射体位置越多时,约束越多,对目标位置求解提供了帮助。
4 基于GA、LM的定位算法
(14)式包含的未知变量为目标位置坐标且是非线性的,故可将求解非线性定位方程组问题转换为求解函数极值的最优化问题。
4.1 GA算法对目标进行初定位
由于散射体的随机组合,当选取的数量较大时,问题的解将呈指数级增长,变为NP问题[21]。鉴于这一情况,遗传算法中的“优胜劣汰”思想可以很好地计算出目标位置,通过模拟自然进化过程搜索最优解[22];虽然散射体位置被约束在散射区域的线段上,但是仍然存在一定的位置模糊。因此,本文采取不同散射体的组合进行求解,然后将最后的目标位置进行聚类,可以进一步提高定位精度。对于该问题的求解,约束条件表示为
(15)
求解步骤如下。
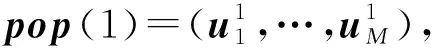
步骤2依据本文的优化问题(15)式,构造适应度函数
fi=fitness(popi(m))=
(16)
步骤3若满足停止条件,则算法停止;否则,依据适应度函数值的大小对种群进行优化,将适应度函数值小的个体淘汰,对保留下来的优良个体计算概率为
(17)
并以概率分布从种群中随机选取M个染色体构成一个新种群newpop(t+1);
步骤4染色体之间的结合;将上一代群体中的优良染色体通过编码以交叉概率Pc=0.8进行交配得到crosspop(t+1);
步骤5对交配后的染色体以变异概率p=0.02使其中的一个染色体的一个基因发生变异,形成群体mutpop(t+1);然后t=t+1,新的种群变为pop(t)=mutpop(t);返回步骤2。
4.2 LM算法对目标进行精定位
采用遗传算法对目标进行粗定位得到一个目标位置的初始值,然后本文利用LM算法[20]进行二次精定位,过程如下。
步骤1由4.1节遗传算法得出的定位结果作为LM算法的初始点记为u(0),选取参数0<β<1,μυ>1且精度选为ξ=0.01,k=0;
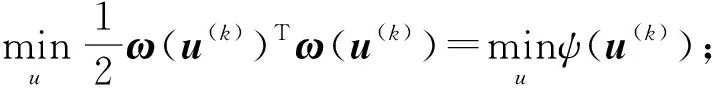
步骤3计算ω(u(k))的雅克比矩阵为
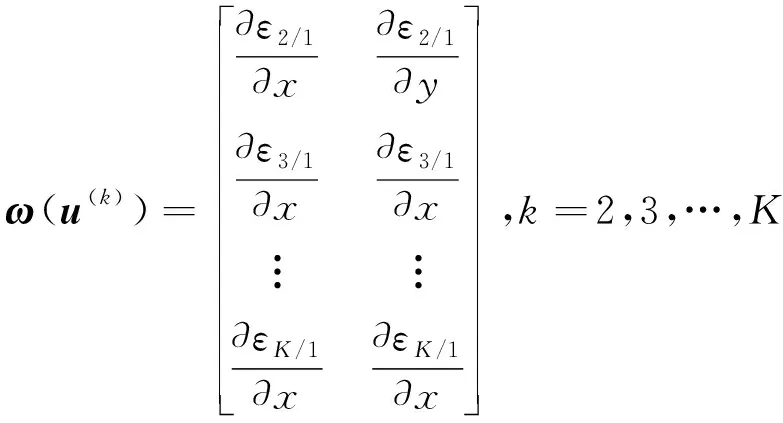
(18)
步骤4计算∇ψ(u(k))=(∇ω(u(k))T)ω(u(k));
步骤5令R=(∇ω(u(k))T)∇ω(u(k)),进而求解方程[R+μI]Δu=-∇ψ(u(k));
步骤6令u(k+1)=u(k)+Δu,计算是否满足循环退出条件,如果不满足则继续计算步骤7;
步骤7若ψ(u(k+1))<ψ(u(k))+β(ψ(u(k)))TΔu,令μ=μ/υ,继续计算步骤8,否则令μ=μυ,返回步骤5;
步骤8令k=k+1,返回步骤2。
以上步骤是基于一次散射体组合完成的一次定位结果,为了提高定位精度选取多个不同散射体组合进行定位,然后利用对多个目标位置进行聚类,能进一步提高定位算法的精度。本文利用放射传播聚类算法(affine propagation clustering, APC)[23]对定位结果进行聚类。传统聚类算法往往需要知道类的个数,而该聚类算法不需要类种类数的先验信息,可以有效地对数据点进行自适应聚类。将目标位置之间的相似度表示为目标间的负欧氏距离,公式为
s(i,j)=-‖ui-uj‖2,∀i,i≠j∈{1,…,M}
(19)
(19)式中,ui,uj为Du内的2个目标位置,将其作为算法的输入。以j为聚类中心的位置点i的权值表示吸引度α(i,j),以i为聚类中心的位置点j的权值表示归属度δ(i,j),分别计算为
将两者在各个点之间不断迭代,当达到最大迭代次数或者聚类中心稳定不变时,算法停止,取聚类结果的平均值作为算法的最优目标位置。
图4为单独利用GA算法以及GA-LM算法的迭代结果。图4中蓝色星星代表搜索到的散射体位置,红色五角星代表目标的真实位置,绿色星号代表算法的迭代结果。
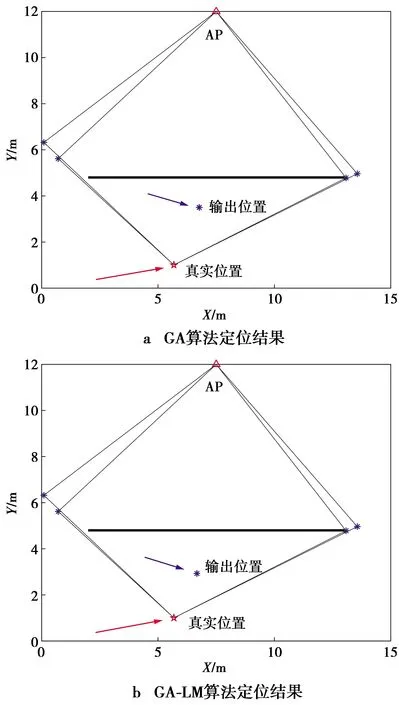
图4 不同算法的定位结果Fig.4 Localization results of different algorithms
对2种算法选取不同测试点进行定位误差统计,结果如表1所示。
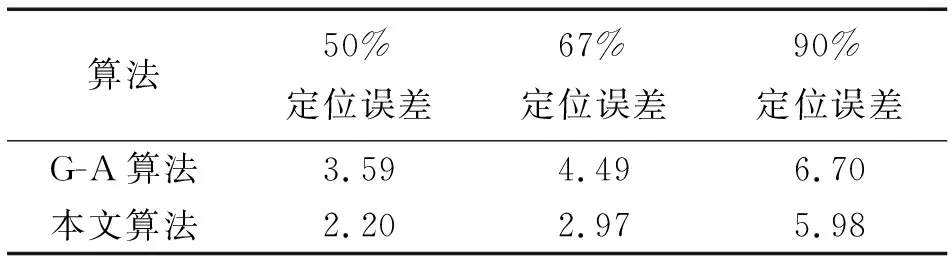
表1 不同定位算法误差统计Tab.1 Error statistics of different positioning algorithms m
5 仿真实验结果
为了分析本文所提算法性能,采用对比分析实验法对本文所提算法进行仿真验证,以图2为例,设置房间的大小为15 m×12 m,定位基站位置设为(7.5 m,12 m)。AOA、TOF的误差均为零均值的高斯白噪声,标准差分别记作σAOA=8°和σTOF=0.3 m,每个实验分别进行200次独立仿真实验。
5.1 不同算法性能对比
将本文所提模型算法分别与文献[14]中的多路径协助定位算法和文献[15]中的多路径三角分解定位算法进行比较,构造一条直达路径构成差分观测值,并设置参数误差。图5为不同算法的定位误差累积分布,从图5可以看出,本文所提算法中值误差为2.2 m,而三角定位算法的中值误差为3.2 m,多路径协助定位算法的中值误差为3.4 m。从仿真结果可以看出,本文所提算法定位精度高于另外2种定位算法,其中,多路径协助定位算法参数估计误差较大,主要由于当多路径定位算法缺少AOD信息时,散射体的模糊区域较大导致定位目标偏离真实值较远,且差分观测值较少。对于移动终端设备来说,获取定位参数AOD较为困难,使得文献[14]及文献[15]中的算法很难应用到实际场景中。
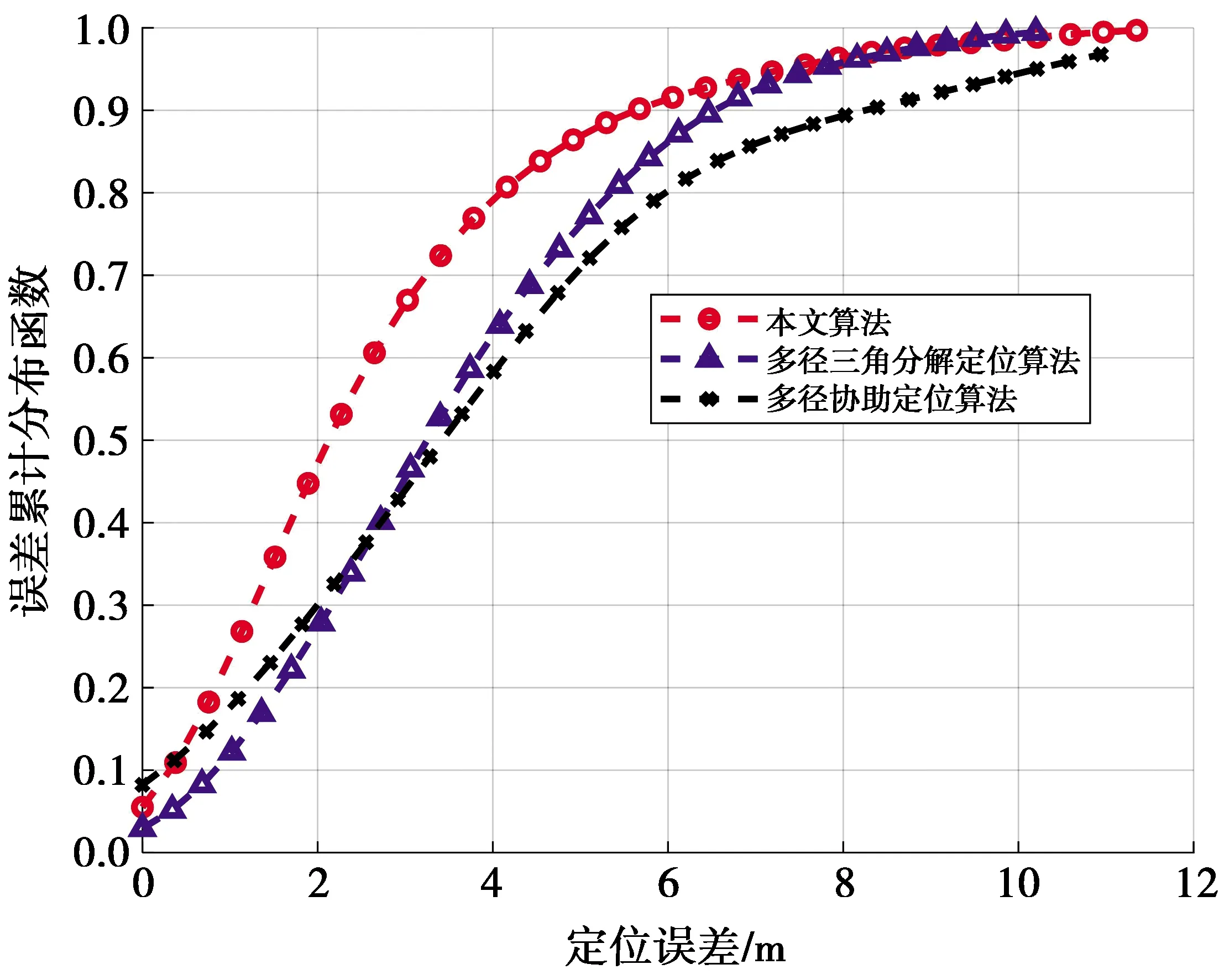
图5 不同定位算法的误差累积分布Fig.5 Error cumulative distribution of different localization algorithms
5.2 散射体个数对定位精度的影响
散射体个数越多,对目标位置的约束等式就越多,因此,增加散射体数量可以提高定位精度。图6为不同散射体个数时的定位误差累积分布,从图6可以看出,当散射体个数为4、6、8时的中值误差分别为2.6、2.3、2.1 m。随着散射体个数增加,定位精度也随之增加,当散射体个数从6增加到8时,中值误差减小较多,为0.2 m,而当散射体个数从4增加到6个时,误差减小较少,为0.3 m。
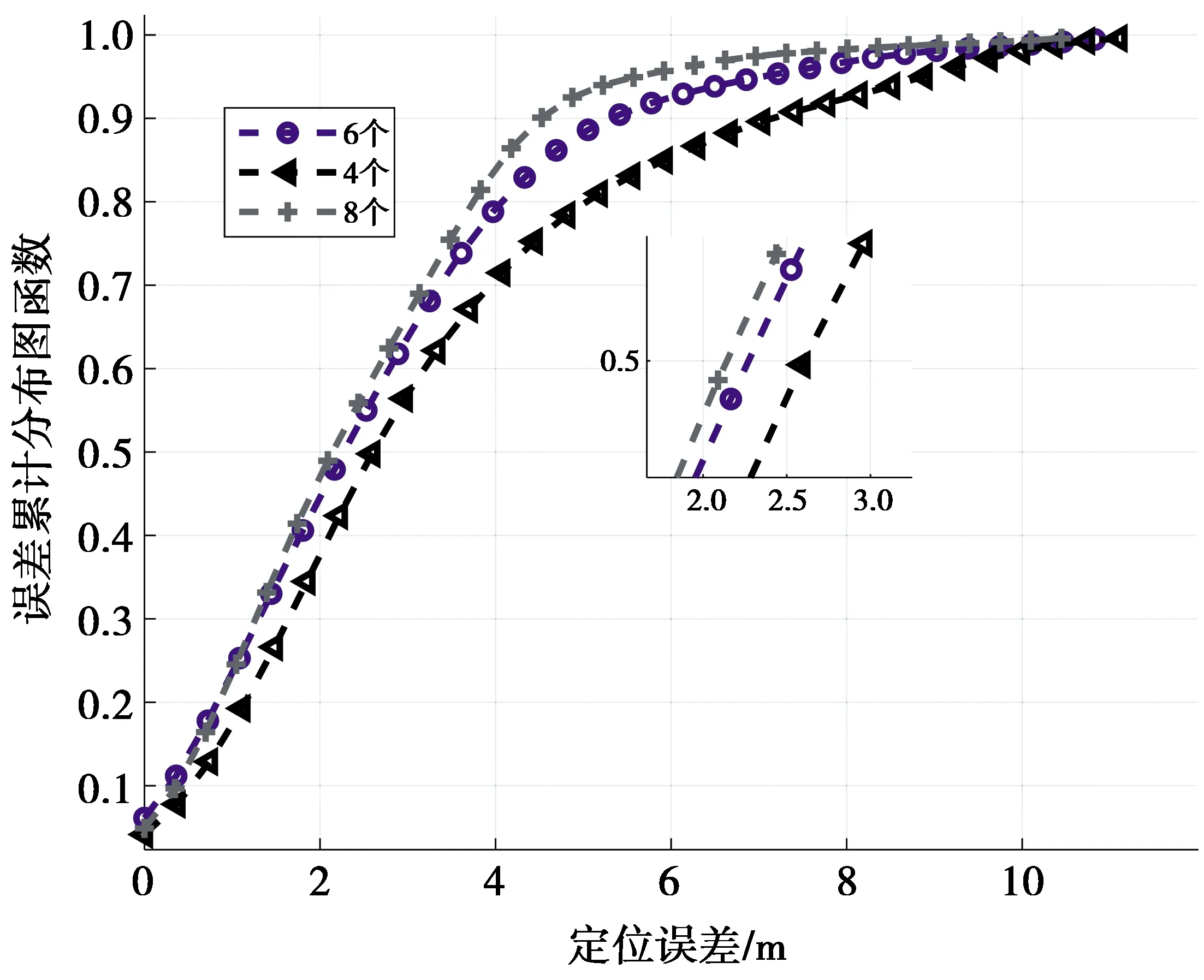
图6 不同散射体个数的定位误差累积分布Fig.6 Cumulative distribution of localization errors of different scatterers
5.3 室内环境大小对定位精度的影响
目标以及散射体可能存在的搜索范围会随着室内环境的大小而改变,因此,室内环境大小对定位精度有着影响。为了探究不同环境大小下的定位精度,本文选取大小为15 m×12 m和30 m×20 m的环境大小作为对比。图7为不同环境大小下的定位误差累计分布,从图7可以看出,环境大小为15 m×12 m时,中值误差为2.4 m;环境大小为30 m×20 m时,中值误差为4.9 m。因此,随着环境大小的减小,定位精度随之提高。

图7 不同室内环境大小的定位误差累积分布Fig.7 Cumulative distribution of localization errors of different indoor environment sizes
5.4 墙壁长度长短对定位精度的影响
本文模型中墙壁长度的长短将会导致非视距范围覆盖面积的大小,因此,墙壁长度的大小对定位精度有着影响。为了探究不同墙壁长度下的定位精度,本文选取墙壁长度分别为11、8、6 m作为对比。图8为不同墙壁长度下的定位误差累计分布,从图8可以看出,墙壁长度为11、8、6 m时,中值误差分别为2.1、2.6、3.4 m。因此,随着墙壁长度的减小,定位精度随之提高。
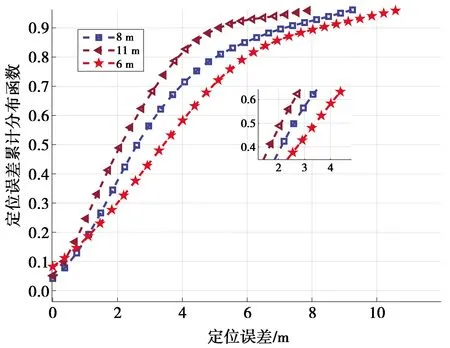
图8 不同墙壁长度的定位误差累积分布Fig.8 Cumulative distribution of localization errors of different wall lengths
6 模拟真实场景测试
6.1 模拟环境介绍
为了验证算法的实用性,本文使用Wireless InSite软件对重庆邮电大学逸夫楼5楼YF508进行模拟测试。该软件主要用于预测分析室内环境以及其他多径传播环境中无线传播及信道特性,能够直接屏蔽物理层,模拟实际场景内物体的反射系数等参数,达到与实测结果吻合的效果。图9为Wireless InSite软件模拟的场景示意图。其中,传播射线的不同颜色代表不同的信号强度。由于该算法只对二维平面进行定位,设置房间大小为13.3 m×14 m,AP坐标设置为(6 m,14 m),散射体分布在中间墙壁两侧端点(0.9 m,8 m)、(12.4 m,8 m)附近,在其目标区域内设置110个目标测试点。

图9 Wireless InSite模拟场景示意图Fig.9 Schematic diagram of simulation scene by Wireless InSite
6.2 参数估计算法测试
图10为测试过程中定位参数估计算法产生的信号二维空间谱图。图10中极值点代表估计到的路径,为了分辨更多路径,采用基于压缩感知的参数估计方法,利用搜索出的多条NLOS路径进行定位。
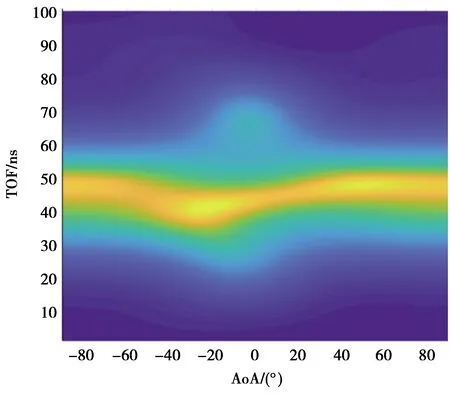
图10 AOA/TOF谱峰图Fig.10 Spectral peak of AOA/TOF
6.3 聚类算法及定位性能测试
图11为路径仿射传播聚类算法的结果,其中,不同的类代表不同传播路径,每个类的均值用于定位的路径参数。图12为模拟真实环境下算法的定位误差累积分布。从图12可以看出,定位中值误差为2.5 m,进一步验证了在室内NLOS环境中实现单基站定位的可行性。
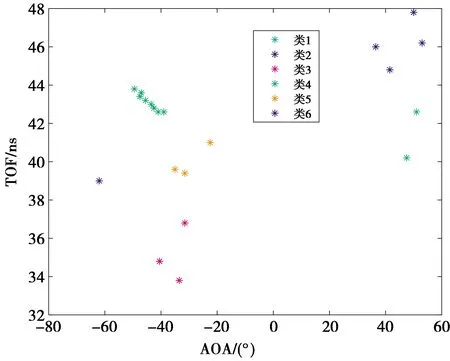
图11 路径聚类结果Fig.11 Result of path clustering
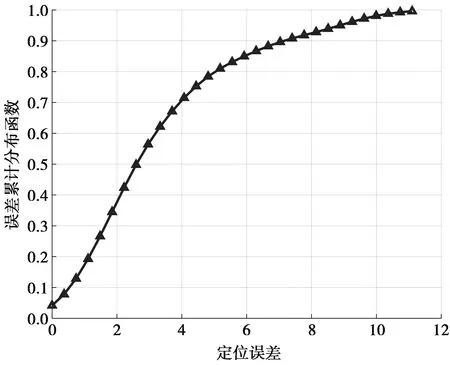
图12 本文算法的定位误差累积分布Fig.12 Cumulative distribution of positioning errors
7 结 论
本文提出了一种基于散射体信息的室内NLOS单基站定位算法。针对NLOS环境下散射体的模糊区域较大问题,首先,结合室内建筑结构的先验信息,对室内建筑结构进行建模,使得模拟参数的构建符合真实场景,仅利用单个基站处理建筑物内部多径传播条件较为恶劣的问题;然后,利用定位参数构建最小化目标定位方程,并将其转换为非线性最小二乘优化问题;最后,由于优化问题的求解存在多种算法,因此结合散射体及目标位置的随机性,本文利用GA、LM算法的结合求出目标的最优位置。通过仿真及模拟场景测试,本文所提算法在NLOS环境下可以达到较高的定位精度。

