基于正交试验法的机翼壁板桁条端部疲劳特性分析

张彦军，王斌团，雷晓欣，朱亮，车承牮

航空工业第一飞机设计研究院，陕西 西安 710089

飞机结构件的疲劳断裂一般出现在有效承力面积发生较大变化即应力集中明显的区域（如开孔、斜削及对称型缺口等结构不连续区域）。这些应力集中区域通常是疲劳裂纹萌生及扩展的源头，而应力集中系数则是描述结构应力集中程度的重要参数，也是多种疲劳寿命预估方法的重要计算参数[1-3]。王向明[4]基于设计制造一体化提出了整体化、结构功能一体化等新概念结构，具有高减重、长寿命等显著优势。袁慎芳[5]提出了一种基于卷积神经网络的疲劳裂纹扩展辨识方法，有效提升了辨识准确率。赵洪利[6]提出了基于贝叶斯动态更新模型对发动机余寿预测的方法。因此，对结构危险部位的理论应力集中系数进行计算和预估，并得出公式化的规律和结论，从而准确估计飞机结构发生疲劳断裂的高危区域位置，得到较为精确的危险点应力值，可为飞行器结构的疲劳-安全寿命预估及设计提供重要的前期数据和理论参考。

本文在有限元分析的基础上，选用正交试验法，分析了某运输类飞机下翼面整体壁板长桁端部斜削结构的关键几何因素对结构应力集中系数的影响，得出了计算该型结构应力集中系数的经验公式，采用细节疲劳额定值（DFR）法给出了疲劳分析结果。

1 长桁端部正交试验设计

长桁端部斜削结构是一处重要的疲劳危险部位，在多型飞机的使用和试验中都暴露出了疲劳问题。为研究重要几何参数对长桁端部斜削结构应力集中系数的影响，利用有限元分析进行正交试验[7-10]。

一般地，长桁斜削设计中的主要几何因素如图1所示，其中因素A为斜削角度，因素B为斜削根部底角半径，因素C为腹板根部倒角半径。

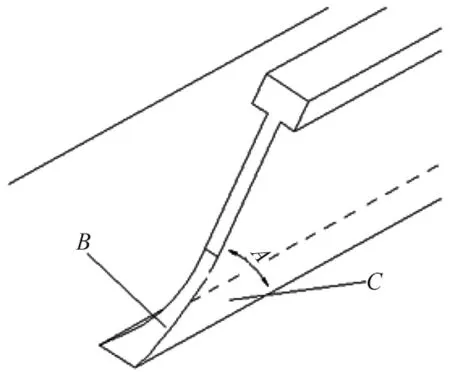
图1 机翼长桁端部斜削结构设计的三种关键几何因素Fig.1 Three key geometrical factors for runout design of wing stringer

各因素的显著性未知，因此需要设计仿真试验进行分析。本文探究上述三种几何因素对应力集中系数的影响，为避免仿真试验次数过多，将每种因素的水平数确定为4个。由于标准正交试验表中并不存在三因素四水平表，因此选择五因素四水平标准正交表，将多余的2 列作为误差列，可将其用于之后进行的极差分析、均方差分析及F检验。根据长桁斜削端典型结构参数，研究上述三种几何因素在4种不同水平下对应力集中的影响（见表1）。

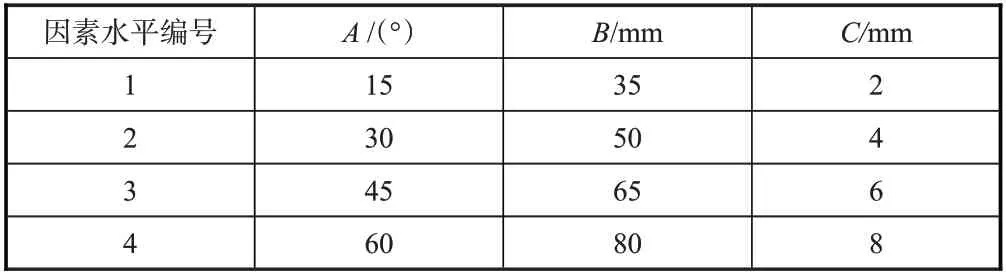
表1 主要几何因素及各因素水平选取Table 1 Key geometrical factors and level selection

2 长桁端部正交应力集中系数计算

在长桁端部斜削结构模型中，改变模型的A、B、C三种几何因素，按照标准正交试验L16(45)前三列的组合安排进行仿真试验，加载形式为单轴拉伸，载荷大小统一为100kN，约束垂直于加载方向的位移，材料参数选取2024-T351铝合金材料参数，见表2。其中，斜削角度为15°、30°、45°、60°时的应力云图如图2所示。

表2 国产2024-T351铝合金材料参数Table 2 Parameters of 2024-T351 aluminum material

图2 长桁端部不同斜削角度仿真试验结果Fig.2 FE analysis result for stringer runout with different runout angles

有限元分析表明，最大危险应力均出现在斜削根部底角过渡圆弧的中点处，以壁板中央平直段截面平均应力作为净截面名义应力，由式（1）计算得出危险点理论应力集中系数，并将结果整理在表3中。

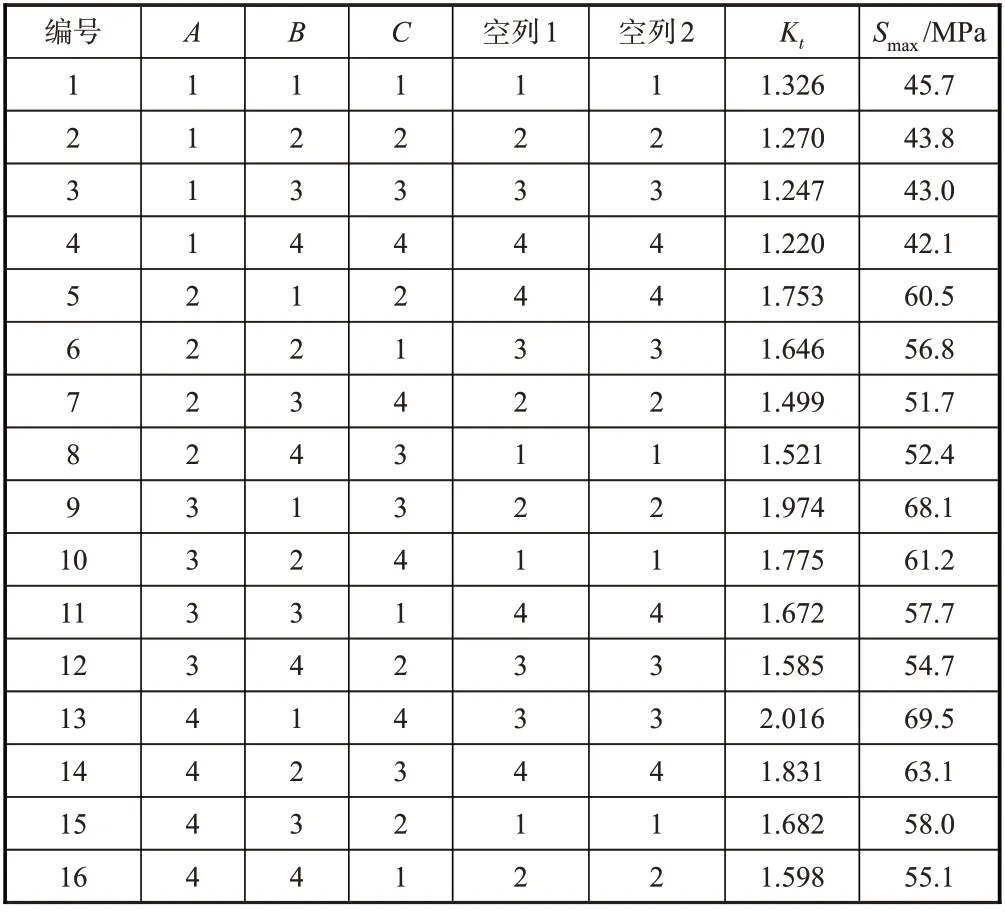
表3 正交仿真试验应力集中系数计算结果Table 3 Stress concentration factor from orthogonal experiment method

式中:Smax为最大主应力；Sn为名义应力。

3 正交仿真试验结果分析

3.1 影响因素分析

对正交仿真试验结果进行分析，得到不同因素和其交互作用的重要性顺序，从而区别主要因素和次要因素，判断因素对试验指标影响的显著程度。同时，正交试验结果还可用于分析试验指标与不同因素之间的关系，即试验指标随因素的变化而变化的规律，为后续试验及研究指明方向。一般地，正交试验结果处理的内容与步骤如图3所示。

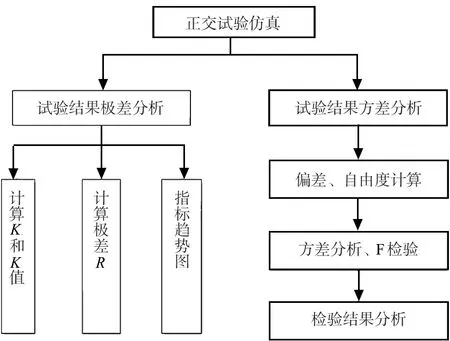
图3 正交试验结果分析流图Fig.3 Analysis flowchart of orthogonal experiment method

定义Kjm为第j列因素m水平所对应的试验指标和，kjm为Kjm的平均值。定义Rj为第j列因素的极差，表示了第j列因素水平波动时，试验指标的变动幅度。Rj的计算公式见式（2）。

由Rj大小，可以判断因素的主次顺序。比较各R值的大小，R值越大则对应因素对试验指标的影响越大，R值越小则对应因素对试验指标的影响越小。对于长桁斜削端应力集中系数正交试验，结合表3的构建形式及仿真结果，其极差分析内容见表4。

将正交试验表4中的空列视为误差列，则根据表4所显示的结果，极差R1＞R2＞R3=Re1＞Re2（Re1、Re2分别为表4中空列1、空列2所对应的R值），即这三种几何参数对长桁斜削端危险部位理论应力集中系数的影响程度由高到低依次为:斜削角度＞斜削根部底角半径＞腹板根部倒角半径。

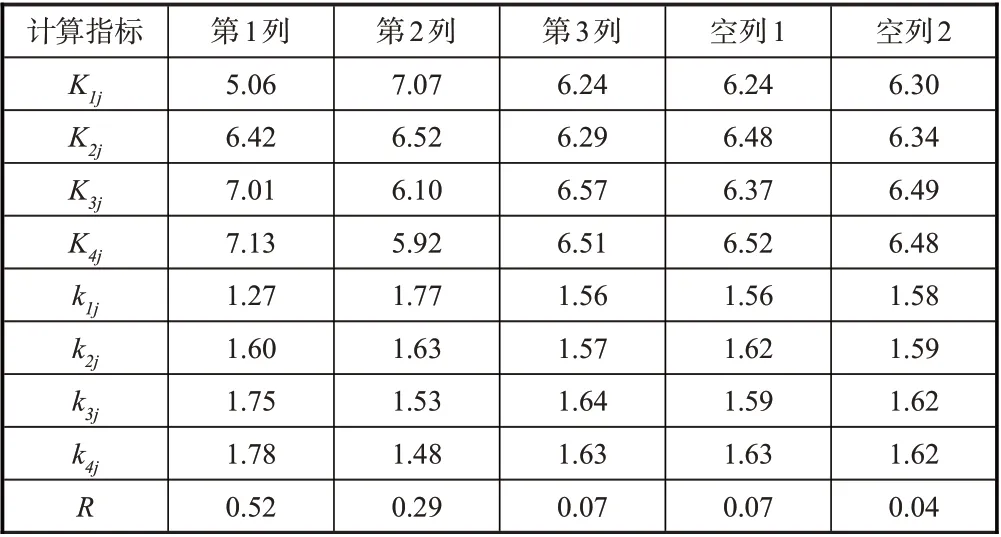
表4 正交仿真试验结果极差分析Table 4 Range analysis of orthogonal experiment method

3.2 方差检验分析

由表4 可知，极差分析无法将正交试验中由于改变试验条件所引起的数据差异与试验误差所引起的数据差异区分开来。除此之外，对于不同因素对试验结果的影响大小无法给出相对精确的数量估计，也无法给出一个普适的标准用于判断某因素对试验指标的作用是否显著。因此，针对极差分析中出现的“盲点”，应设计方差分析方案，完成因素显著性分析。

方差分析的主要思路是将数据的总变异的来源分解为两部分，一部分由因素引起，另一部分由误差引起，然后即可构造F统计量，完成F检验，从而判断不同因素对试验指标影响的显著性。

本节中方差分析的流程为:

（1）由正交试验所得试验指标计算各列偏差平方和、误差偏差平方和以及总偏差平方和，计算公式及相互关系由式（3）～式（5）给出

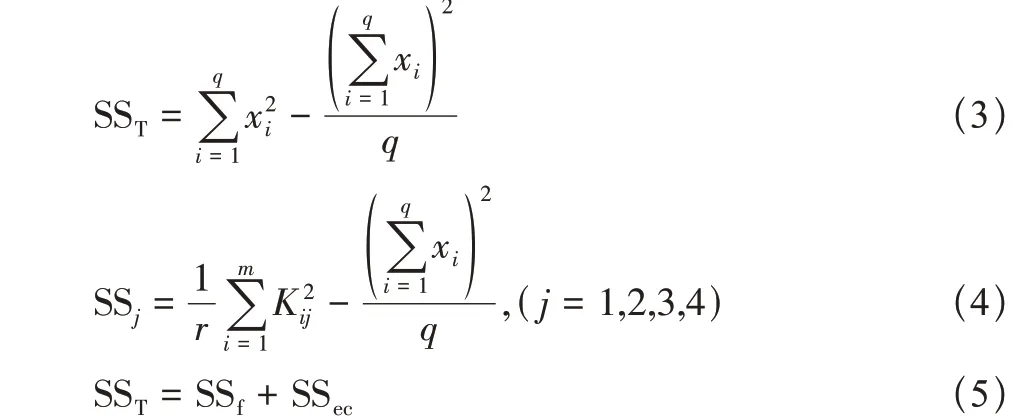
式中:SST为总偏差平方和；SSj为对应列偏差平方和；试验总次数为q；第i次试验得到的试验指标为xi；因素水平数为m；每个水平作r次重复，r=q/m；SSf为因素A、B、C对应的偏差平方和；SSec为空列1、空列2对应的偏差平方和。

对于本文进行的正交仿真试验，以应力集中系数为试验指标，其偏差平方和计算结果见表5。

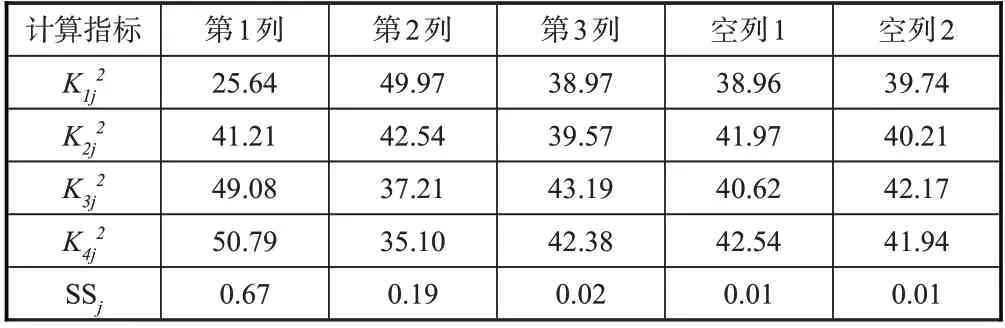
表5 试验指标偏差平方和Table 5 Quadratic sum of deviation for experiment result

（2）进行自由度分解与方差计算，其中误差的自由度通常不应小于2，若误差自由度dfe过小，由于F检验的灵敏度具有一定局限，那么在某些情况下，即使因素对试验指标存在影响，F检验也无法判断出来。因此，为了适当增大误差自由度，提高F检验的灵敏度，在检验不同因素的显著性之前，应先比较因素方差与误差方差，如果因素方差小于两倍的误差方差，则应将该因素的偏差平方和及自由度并入误差的相应指标中，从而增大误差的自由度，使F 检验更为灵敏。

自由度及方差通过下列公式进行分解和计算

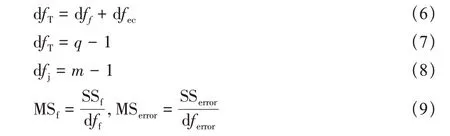
式中:dfT为总自由度；dfj为因素自由度；误差的自由度等于所有空列的自由度之和；MS为方差。

（3）建立F统计量，设计方差分析表格，完成F检验。确定因素自由度与误差自由度后，则定义Fn为自由度为（dff，dferror）的F分布随机变量，Fn即因素n的F比，由式（10）进行计算

在F 分布表上查找显著性水平α下的临界值Fα(dff,dferror)，α的数值通常很小，那么Fn＞Fα(dff,dferror)的概率也很小，但如果试验呈现出这种结果，那么便可以认为在显著性水平α下，某因素的水平变化可以对试验指标产生显著影响，这时得出的结论不成立的可能性仅为100α%。一般地，α的选择根据问题的具体精度要求而定，对结论的置信度要求越高，α的取值应当越小。对于本节内容而言，进行F 检验之后，则可以判断三种几何因素对长桁斜削端危险部位应力集中系数的影响的显著性，方差分析结果见表6。

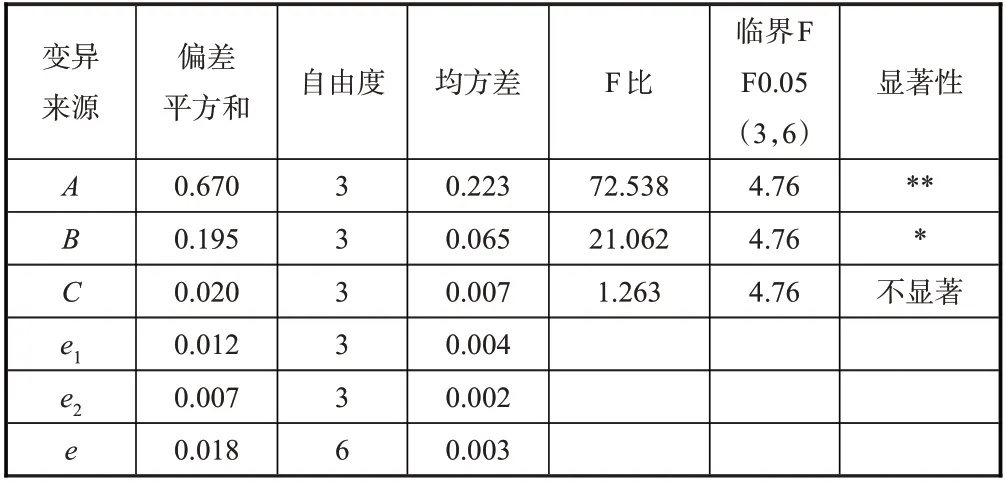
表6 正交仿真试验结果方差分析Table 6 Analysis of variance for orthogonal experiment result

由F检验可知，因素C（腹板根部倒角）对应力集中系数的影响不显著，而因素A（斜削角度）和因素B（斜削根部底角半径）对应力集中系数的影响较为显著，是影响该型结构疲劳性能的主要几何因素。

3.3 理论应力集中系数拟合

本节讨论了三种长桁斜削端重要几何参数对理论应力集中系数的影响，通过对正交试验结果的统计处理，得到影响应力集中程度的主要两种几何参数，即斜削角度与底角圆弧半径，可忽略腹板根部倒角半径对应力集中系数的影响。

因此，长桁端部斜削结构的应力集中系数可用仅含斜削角度和底角圆弧半径两类变量的工程经验公式来表示。

将正交仿真试验结果在Matlab 软件中进行数据拟合，对相关几何变量进行无量纲化处理，得到理论应力集中系数Kt的二元函数工程经验公式

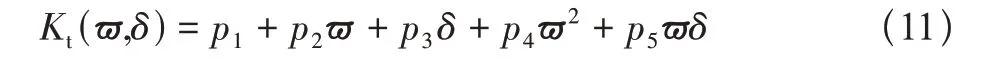
式中:形状参数ϖ=ω/，ω为斜削角；δ=ρ/H，ρ为斜削根部底角半径，H为桁条高度；p1=0.816，p2=4.159，p3=-0.021，p4=-2.778，p5=-0.72，如图4所示，拟合曲面与有限元计算值之间的均方根误差约为3.763%。

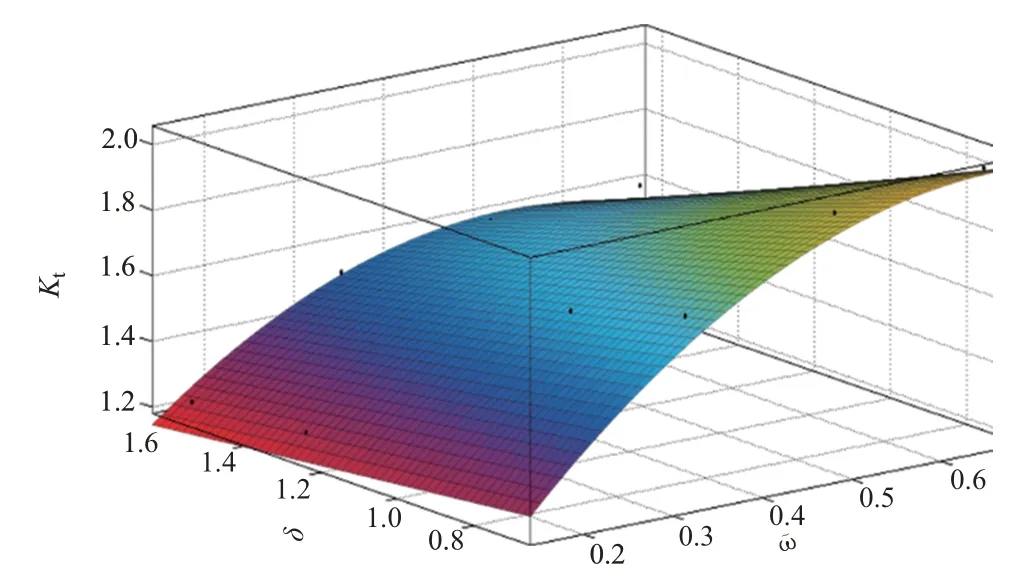
图4 理论应力集中系数随关键几何参数变化Fig.4 Relationship between stress concentration factor and key geometry factors

整体壁板式长桁端部斜削结构理论应力集中系数二元函数工程经验公式（11）表明了危险点应力集中程度与关键几何因素的变化关系，也说明了两种重要几何参数间存在明显的交互作用，同时也表明了两种几何参数对应力集中系数产生影响的显著性存在差异。

在实际工程应用中，利用本节所得工程经验公式可以方便快捷地确定应力集中系数，为飞机机翼长桁强度设计和疲劳预估提供重要参考。

4 分析方法与试验结果

4.1 疲劳分析

（1）DFR法分析方法及结果

DFR是可以体现飞机结构危险部位所固有的疲劳属性的重要参数，它表示在应力比R为0.06、细节寿命具有95%置信度和95%可靠度的情况下，结构可以达到100000次循环疲劳寿命的局部最大应力值。

长桁端部斜削结构属于相似细节数少于100的无机械连接的离散结构，铝合金材料按应力集中结构[2]计算

联立式（13）～式（16），即可计算结构细节在95%置信度、95%可靠度下的疲劳寿命

式中:σm0为σa=0时的破坏应力；S为S—N曲线的斜度参数；

X=S(5-lgN)；Y=[(σm0-0.53DFR)σα]/[0.47DFR(σm0-σm)]；Z=[(1-R)(σm0-0.53DFR)σmax]/[DFR(0.94σm0-0.47(1+R)σmax)]；铝合金材料的σm0=310MPa，S=2。

对于本次试验所设计的长桁端部斜削结构件，在应力比R=0.06 的条件下，计划施加峰值为620kN 的循环载荷。将材料参数及三维模型导入ANSYS WORKBENCH 软件中进行有限元分析，限制试件在偏心弯矩作用下产生的弯曲变形，计算危险部位最大应力，得到关键部位应力云图，如图5所示。

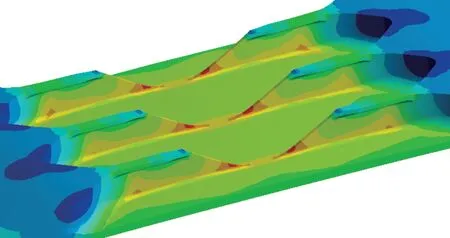
图5 长桁端部斜削危险部位应力云图Fig.5 Stress distribution of fatigue critical position at stringer runout

根据应力分析结果，最大载荷620kN 所对应的长桁端部斜削部位最大应力为σmax=197.56MPa，试验件壁板毛面积尺寸为510mm×14.5mm，计算毛面积参考应力σref，并得到应力集中系数为

根据参考文献[2]，查其中图5-11 缺口材料的DFRbase值，得到DFRbase= 83.1MPa。同理可查得本文结构件对应的粗糙度系数F=1.18。6个基本相似细节，得到RC= 1.31。代入式（12），可得到结构细节DFR值为128.5MPa。

该部位疲劳可靠性系数FRF=1.5，机翼下翼面的空地损伤比λ= 0.9。按DFR计算得到该部位的疲劳寿命为

（2）名义应力法分析方法及结果

名义应力法疲劳寿命预估有以下假设:对于存在应力集中的任意机械结构件，若材料相同、施加的循环交变载荷谱相同、危险部位应力集中程度相同，则具有同样的疲劳寿命。

名义应力法寿命预估的主要步骤为:（1）通过对试件三维模型的有限元分析，得出疲劳失效危险区域的位置；（2）求出试件在承受疲劳峰值载荷时的理论应力集中系数以及相应的名义应力；（3）根据具体的循环载荷要求确定相应的名义应力循环载荷谱，本节对长桁端部斜削结构的疲劳分析，应力比取0.06；（4）对材料（2024-T351 铝合金）的S—N曲线进行修改，并进行必要的插值计算，在S—N曲线中查询所研究试件危险部位的最大应力水平所对应的疲劳失效周次，也可在插值后得到的某应力集中系数下的S—N曲线中查找试件最大名义应力所对应的疲劳寿命；（5）由Miner累积损伤理论对结构件疲劳寿命进行预估。

本文所研究的长桁端部斜削结构所采用的材料均为2024-T351 高强度铝合金，这种铝合金被广泛应用于下翼面的桁梁结构中，其S—N曲线如图6所示。

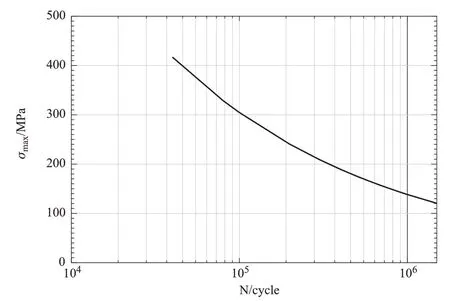
图6 2024-T351铝合金S—N曲线(R=0.06)Fig.6 S—N curve of 2024-T351 aluminum(R=0.06)

由图5 可知，在峰值载荷为620kN 的疲劳载荷作用下的长桁端部斜削结构，其最大应力出现在斜削端部过渡底角圆弧的中点处。由于本节使用的S—N曲线为50%存活率下的应力—寿命曲线，故据此预估得到的疲劳寿命均为中值疲劳寿命，预估结果见表7。

表7 名义应力法疲劳寿命预估结果Table 7 predicted fatigue life using nominal stress method

4.2 试验结果

疲劳试验结果表明所有正常失效的长桁端部斜削疲劳试验件的典型破坏部位均位于长桁斜削底角圆弧的中点附近（见图7）。

图7 长桁端部斜削结构典型疲劳破坏部位Fig.7 Result of fatigue test for wing panle with stringer runout

试验件共5 件有效数据，寿命分别为273401、405135、355631、297030、208785。试验子样大小n1= 5，则

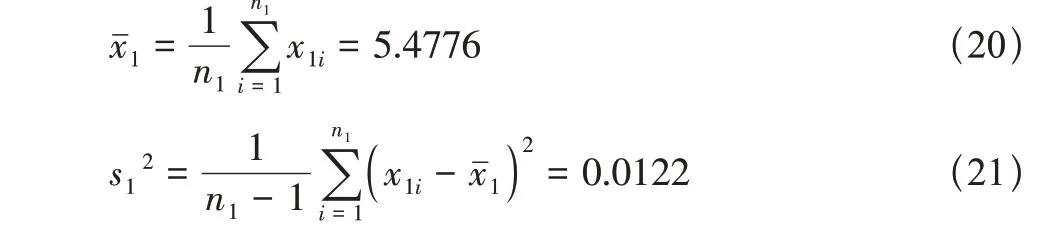
峰值载荷为620kN下，试验件的中值疲劳寿命为

则在应力比R=0.06，最大载荷为620kN的情况下，试验件中值疲劳寿命为300331次。

试验计算结果与三长桁整体壁板疲劳试验结果相比，疲劳危险部位一致，计算结果与试验结果吻合较好，且DFR方法预测结果更接近试验结果。

5 结论

本文采用正交试验法研究了整体壁板长桁斜削端部的关键几何参数下的应力集中系数，给出了应力集中系数的理论表达式，并对比了工程算法疲劳寿命与试验疲劳寿命，可得出如下结论:

（1）通过对整体壁板长桁端部斜削结构的斜削角、斜削角底部圆角半径、腹板根部圆角半径三个参数的正交试验分析，表明斜削角对应力集中影响最大，即对疲劳寿命影响最大。

（2）通过二元函数拟合给出了整体壁板长桁斜削端细节的应力集中系数的理论表达式，可便于工程计算。

（3）采用工程常用的细节疲劳额定值DFR法计算了整体壁板长桁斜削结构细节的疲劳寿命，计算结果与三长桁整体壁板疲劳试验结果相比吻合较好，疲劳破坏位置一致且循环次数接近。