需求风险共担下PPP项目资本补偿决策研究

蒋 贾 霜，吕 俊 娜

(1.重庆交通大学 经济管理学院，重庆 400074； 2.西南交通大学 希望学院，四川 成都 610400； 3.广西交通投资集团有限公司，广西 南宁 530022)

0 引 言

轨道交通PPP项目属于典型的准经营性项目，广泛存在运营期收入不足以覆盖昂贵的建造、运营和维护成本的现象，社会资本难以获得合理的回报[1-2]。政府有必要提供合理的补偿，使得社会资本参与的项目具有投资可行性。资本补偿是中国政府鼓励社会资本参与轨道交通PPP项目的常见补偿机制之一，是特许协议关键参数之一[3-4]，其数量过小则不足以吸引社会资本参与PPP项目的建设，反之则会损害政府和公共利益[3-5]。因此，合理确定资本补偿数量，对PPP项目成功融资至关重要。Carmichael等[3]针对准经营性PPP项目，从社会资本的角度构建了政府资本补偿决策模型，得到了政府最小资本补偿比例。叶苏东[6]基于净现值法建立了混合补偿(资本补偿+运营补偿)的补偿决策模型。吕俊娜[7]从政府和社会资本不同的投资基准条件出发，利用传统的净现值方法得到轨道交通PPP项目下双方都满意的资本补偿可行区间。吕俊娜等[4]认识到需求不确定性以及最低需求保证对社会资本进行资本补偿决策的重要性，通过实物期权和博弈论相结合的方法，构建了基于最小客流量保证下轨道交通 PPP 项目资本补偿决策模型及合作博弈模型。

事实上，在轨道交通PPP项目中，需求的不确定性是造成项目失败的主要原因之一[8]。需求保证/限制能有效解决社会资本因需求不足致使收入过低的问题，还能让政府回收部分超额收入来防止公共利益受损。因此社会资本和政府通常会采用需求保证/限制(即最低需求保证和超额需求共享)来合理共担需求风险[9]。中国已有不少轨道交通PPP项目采用了资本补偿和需求保证/限制来保障项目的正常运行，比如北京地铁4号线、14号线和16号线等。这种需求风险共担机制必然会给项目带来直接的价值[10-11]，并减少资本补偿决策的风险分布，有必要将其价值考虑进资本补偿决策中。

综上所述，本文通过二叉树模型和MC仿真相结合的方法来模拟项目需求的不确定性变化，建立了需求保证/限制价值模型和考虑其价值下的政府资本补偿比例模型，通过算例分析确定了需求保证/限制的复合期权价值及最小资本补偿比例。本文所建模型拥有多种属性，可以描述需求保证/限制期权价值及出现次数的概率分布，还可以显示出政府提供需求保证/限制对政府资本补偿决策风险状况的影响。

1 模型构建

1.1 问题描述

某市拟采用PPP模式建设某轨道交通项目，建设期t年，特许运营期T年，特许运营期到期后，社会资本需无偿交付项目与政府。项目建设总投资为I，政府的资本补偿比例为λ(0≤λ≤1)，政府资本补偿额为λI，社会资本建设投资额为(1-λ)I，为了方便计算，假设政府和社会资本均在建设初期一次性投入建设资金。政府拥有资本补偿部分的所有权，社会资本需在特许运营期间租赁该部分，每年租金为R且运营期间保持不变。运营收入分为票务收入和非票务收入，其中票务收入是轨道交通运营收入的主要收入来源[12]，非票务收入包括广告及站内商业收入，通常认为非票务收入是票务收入的f倍[13]。政府通过提供需求保证/限制来与社会资本共担需求风险，双方约定需求保证上下限分别为DO和DU，当实际需求D小于需求保证下限DU时，政府将根据保证下限DU与实际需求D之差提供补贴；当实际需求D大于需求保证上限DO时，政府将按照实际需求D与保证上限DO之间差额的百分比a与社会资本共享超额收益；否则由社会资本自行承担需求风险[9]。

1.2 二叉树模型

轨道交通PPP项目具有较大的不确定性，为了方便计算，本文假设需求不确定性是项目不确定性唯一来源[4]。二叉树模型(binomial lattice)源于金融界的期权定价理论，主要用来描述随时间推移而变化的不确定性变量[14]，已有许多学者采用二叉树来描述项目需求的不确定性[9，11]。假设在特许运营期T内，市场无套利，需求上下波动概率及幅度都不会变化。以年日均需求D来衡量需求的变化情况，运营期第i年的实际需求为Di(i=1，2，…，T)，DPi是轨道交通PPP项目特许运营期第i年的需求预测值。通常认为初始需求D1呈三角分布[12]，均值为运营期第1年需求预测值。采用需求预测值计算年日均需求D的预期年增长率α[15]：

(1)

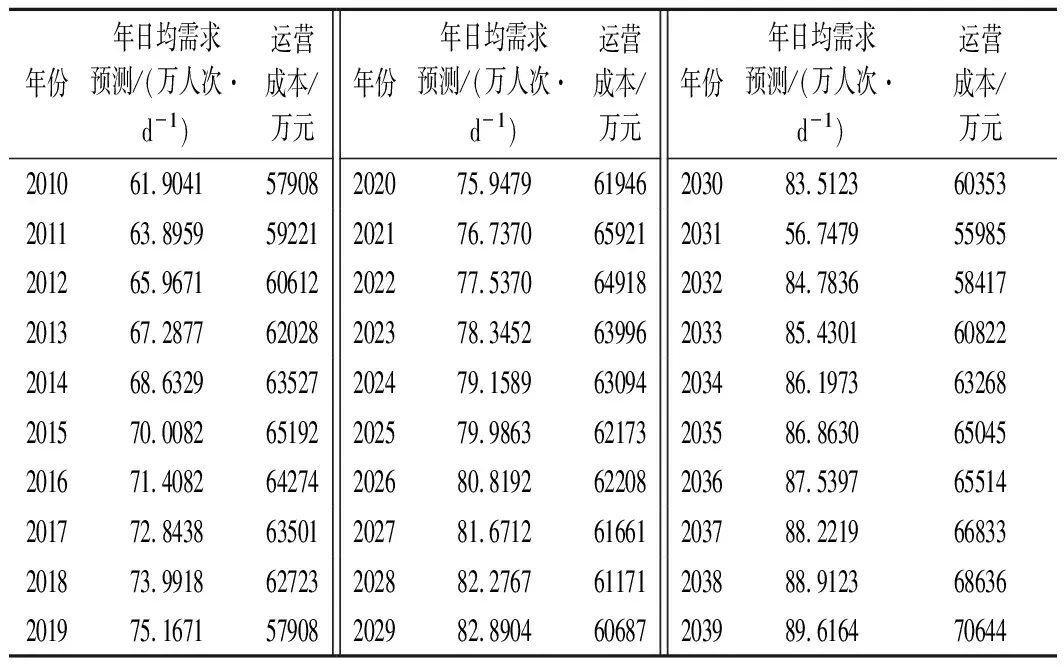
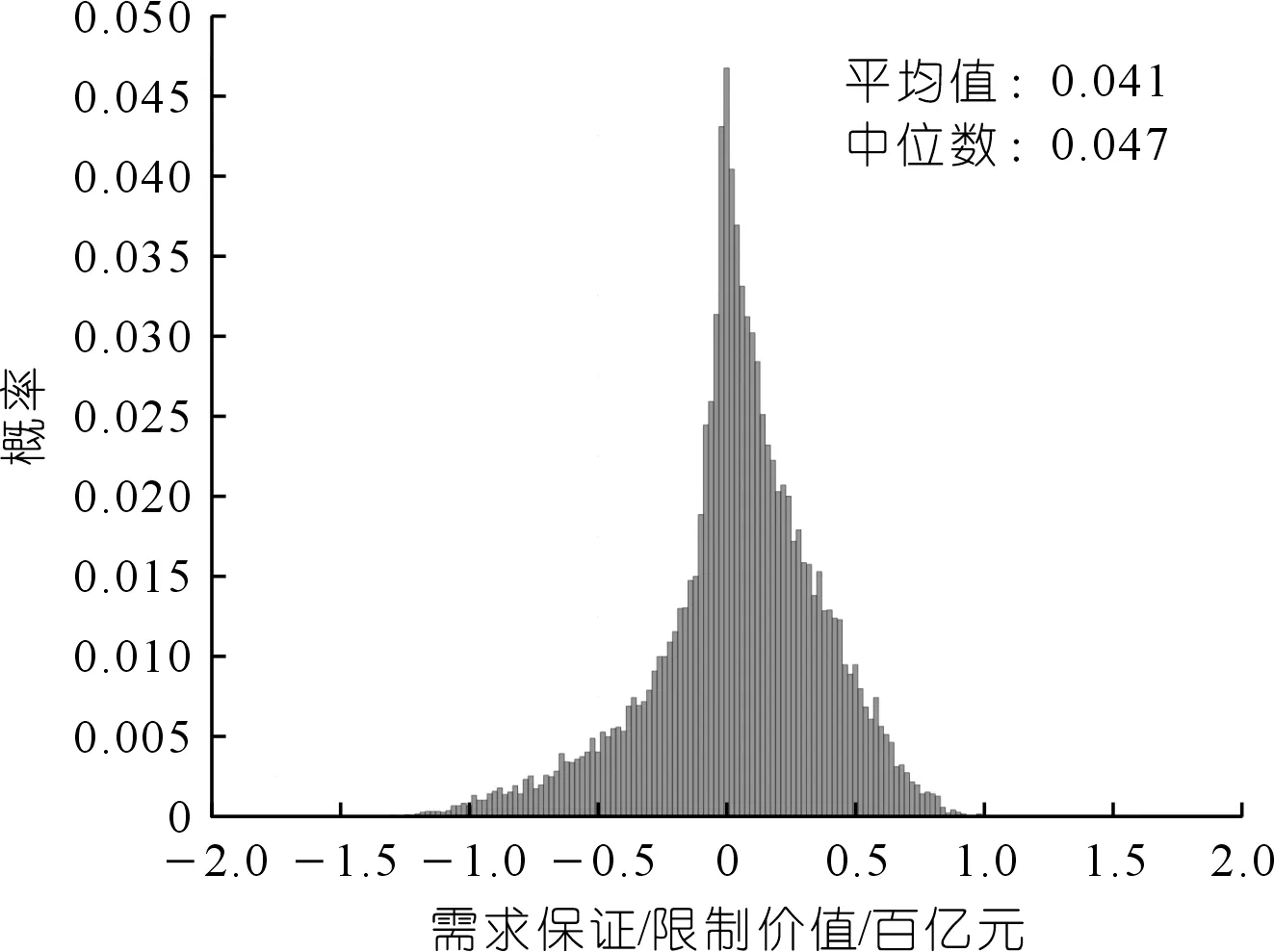
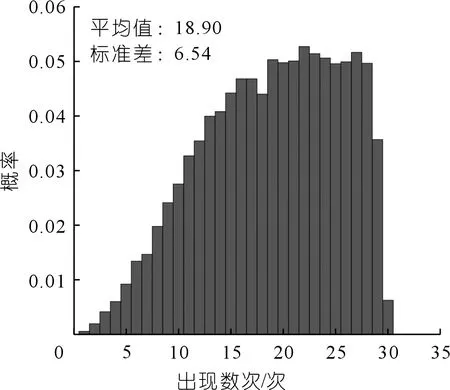
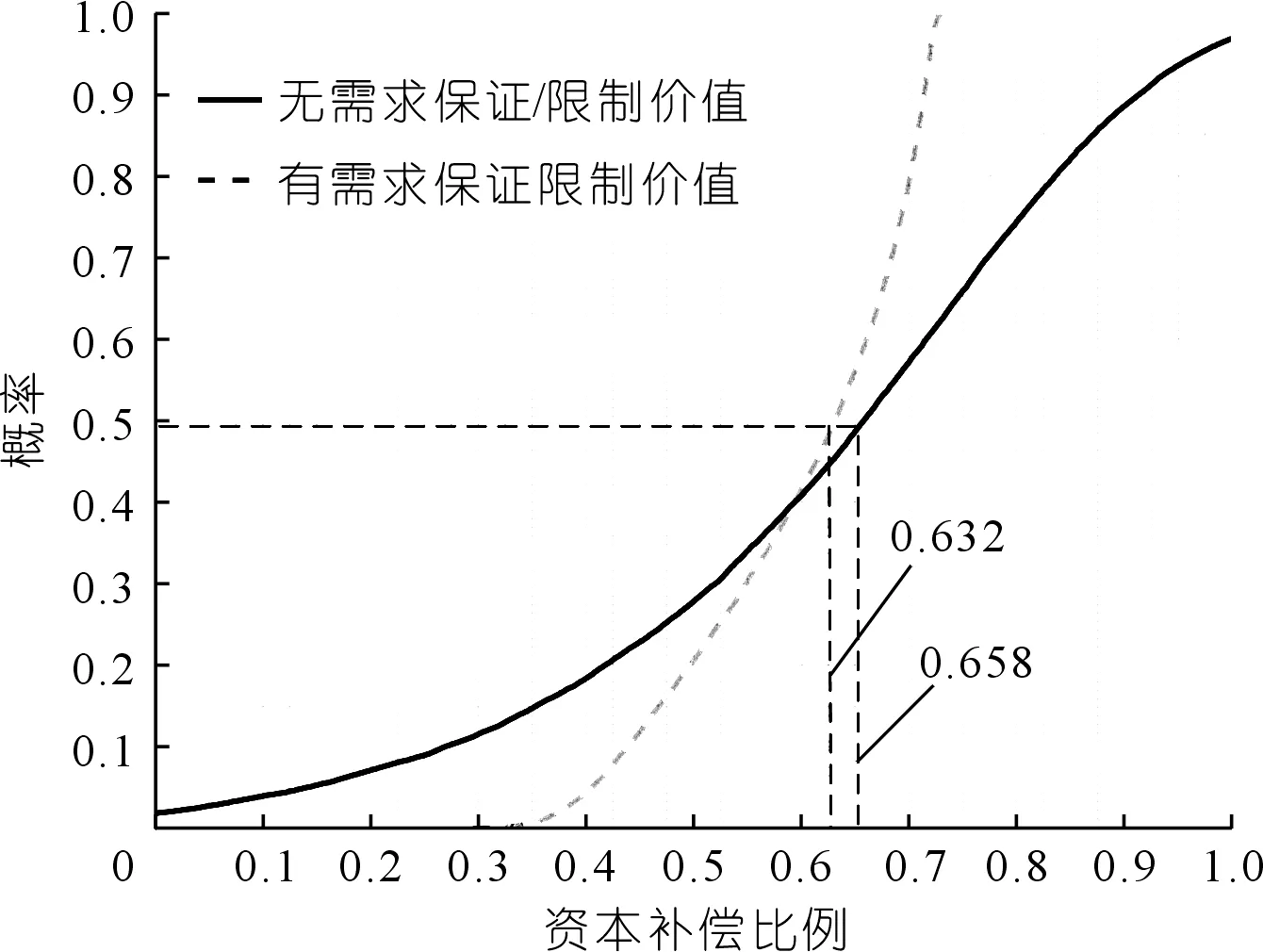
本文利用二叉树模型将每年划分为12个阶段，即T=1个月=1/12 a，整个特许运营期共划分为12×(T-1)个阶段。下个月的年日均需求D取决于当前阶段的年日均需求D向上或者向下运行，上行和下行倍数分别为u和d，其中u>1和0

(2)

式中：年波动率σ由类似项目需求历史数据得到。

采用MC法沿二叉树模型随机生成多条年日均需求的路径，每一条路径上得到的特许运营期每一年的年日均需求Di(i=1，2，…，T)都视为沿该路径所得的未来年日均实际需求，为了让二叉树模拟的数据合理，还需要用轨道交通年日均最大需求对二叉树进行微调，所有模拟的年日均需求均不超过年日均最大需求。然后利用每条路径的年日均需求数据得到该条路径上的政府需求保证的期权价值和政府资本补偿比例。

1.3 需求保证/限制价值模型

假设DOi和DUi(1≤i≤T)分别代表特许协议中规定的特许运营期第i年需求保证的上限和下限，第i年预测票价为Pi，a(0≤a≤1)是出现超额收入时政府可分得的超额部分的百分比。对于社会资本而言，最低需求保证可视为一系列欧式看涨期权，超额需求共享可视为一系列欧式看跌期权，需求保证/限制可视为这两种期权组成的复合期权：当第i年实际日均需求Di小于DUi，则执行看涨期权，最低需求保证第i年的保证价值为MGi=max{0，(DUi-Di)×365×Pi}；当第i年实际日均需求Di大于DOi，则执行看跌期权，超额需求共享每年的保证价值为TCi=max{0，a×(Di-DOi)×365×Pi}。特许运营期最低需求保证和超额需求共享期权价值分别如式(3)和式(4)所示：

(3)

(4)

式中：rf表示无风险利率。结合最低需求保证和超额需求共享的期权执行情况，可以得到需求保证/限制的复合期权价值为

(5)

1.4 考虑需求保证/限制价值的资本补偿决策模型

资本补偿是特许协议关键参数之一，其数量大小直接关乎项目的成功运行。本文在文献[7]的基础上探讨考虑需求保证/限制价值下能满足社会资本投资条件的最小资本补偿比例。通常社会资本投资PPP项目的基准条件与社会资本的期望投资回报率e(e>0)和其参与PPP项目的资金总投入Ic有关[7，13，16]。由于轨道交通需求具有不确定性，本文的资本补偿可考虑需求保证/限制价值下社会资本投资轨道交通PPP项目的基准条件为

(6)

式中：NPV表示社会资本在建设初期的净现值；t是建设期；Yi表示特许运营期间的运营收入，由票务收入PWi(PWi=Di×Pi×365)和非票务收入组成，非票务收入可用票务收入的f(0

(7)

式中：r是社会资本采用的折现率，一般用加权平均资本成本来表示折现率，即：

r=Ierf+Ilrl(1-s)

(8)

式中：Ie是社会资本股本投资占社会资本建设投资的比例；Il是社会资本债务投资占社会资本建设投资的比例，且Ie+Il=1，rl是贷款利率，s是企业所得税。

由式(6)和式(7)可推导出能满足社会资本投资基准条件的资本补偿比例为

(9)

由式(9)可得满足社会资本投资基准条件的最小资本补偿比例为

(10)

需求的不确定性会使得最小资本补偿比例λmin也具备一定的不确定性，得到的λmin是一个概率函数。只有λmin满足社会资本概率期望值θ时，社会资本才会投资项目[13]，即：

P(λmin)≥θ

(11)

2 算例分析

2.1 项目概况

北京地铁4号线是中国首个轨道交通PPP项目，具有重要研究价值。北京地铁四号线建设期总投资为153亿元，建设期5 a，特许运营期30 a，每年的非票务收入是该年票务收入的0.14倍，项目租金为每年4 250万元，社会资本和政府在项目特许权协议中预测票价为3.91元/人次，考虑到通货膨胀及人均收入增长等因素，票价每3 a调整一次，预测每次涨幅为3%，社会资本期望投资回报率为15%，社会资本概率期望值为0.5，利用类似项目需求历史数据可得年波动率σ=10%[12]。政府和社会资本决定采用需求保证/限制来共担需求风险：需求保证上下限分别是需求预测值的1.1倍和0.8倍，当实际需求大于需求保证上限时，政府分走80%的超额收入。特许运营期初中国的长期国债年利率为3.86%，即rf=3.86%，人民币5 a期以上贷款利率为5.94%，即rl=5.94%，社会资本的企业所得税税率为15%，社会资本投资PPP项目的资金来源包括1/3的股本资金和2/3的债务资金，社会资本的企业所得税税率为15%。假设项目初始年日均实际需求D1服从最小值为46.4万人次/d、均值为61.90万人次/d和最大值为71.19万人次/d的三角分布。经测算该轨道交通项目年日均需求上限值为160.9万人次/d，项目特许经营期内的需求和运营成本预测数据如表1所列[7，17]。

2.2 数据处理

根据式(8)，可得r=1/3×3.86%+2/3×5.94%×(1-15%)=4.65%。由表1数据和式(1)可得预期年增长率α=[ln(89.616 4/61.904 1)]/30=1.23%。根据式(2)可获得二叉树的上行倍数u为1.029，下行倍数d为0.972，上下运行概率q为0.509。

表1 需求和运营成本预测Tab.1 Forecast of demand and operation costs

2.3 仿真结果

采用MC法沿二叉树模型随机生成20 000条年日均需求路径。结合式(3)、(4)和式(5)，获得需求保证/限制期权价值及出现次数的概率分布，结果如图1～2所示。

图1 需求保证/限制期权价值概率分布Fig.1 Probability distribution of demand guarantee/limit option value

图2 需求保证/限制次数概率分布Fig.2 Probability distribution of demand guarantee/limit times

图1展示了该项目所有可能的需求保证/限制期权价值及其概率分布。通过模拟得到，需求保证/限制期权价值的范围为-138.65亿～101.86亿元，平均值为4.14亿元，中值为4.66亿元，标准差为32.52亿元。从模拟结果可知，需求保证/限制期权价值高昂，有必要将其价值考虑到资本补偿决策中来，本项目的需求保证上下限取值更有利于社会资本获取更多利益。

图2展示了需求保证/限制产生期权价值次数的概率分布，需求保证/限制期权次数的平均值为18.90次，标准差为6.54次。在项目特许运营期内，不产生需求保证/限制期权价值的概率极小，这意味着在本项目中，需求保证/限制在绝大概率上都会产生价值，说明了考虑需求保证/限制价值的必要性。

根据随机生成的20 000条年日均需求路径，结合文献[7]和式(10)，可得考虑需求保证/限制和不考虑需求保证/限制价值情况下的最小资本补偿比例的累计概率分布，如图3所示。由图3可以看出，考虑需求保证/限制期权能有效缩减最小资本补偿比例的范围。通过模拟，考虑和未考虑需求保证/限制价值的标准差分别为0.104和0.250，可见考虑需求保证/限制价值能有效降低最小资本补偿比例的不稳定性，更有利于政府和社会资本进行资本补偿决策。考虑和未考虑需求保证/限制价值的资本补偿比例的平均值分别为0.602和0.622，考虑和未考虑需求保证/限制价值的资本补偿比例的中值分别为0.632和0.658。结合式(11)可得，考虑需求保证/限制期权价值时，政府以0.632的资本补偿比例(即资本补偿数量为96.70亿元)就可以吸引社会资本投资项目；未考虑需求保证/限制期权价值时，政府需以0.658的资本补偿比例(即资本补偿数量为100.67亿元)来满足社会资本的投资要求，可见在该项目下，考虑需求保证/限制价值将使得政府能以更少的资本补偿来吸引社会资本参与项目。

图3 考虑和不考虑需求保证/限制价值的 最小资本补偿比例Fig.3 Minumum capital compensation ratios with and without demand guaranteel limit value

3 结 论

资本补偿是轨道交通PPP项目特许协议中的重要参数之一，其数量大小直接决定项目的成败。需求保证/限制是政府和社会资本合理共担需求不确定风险的有效途径。中国已有不少轨道交通PPP项目采用了资本补偿和需求保证/限制来保障项目的正常运行。针对需求保证/限制下轨道交通PPP项目资本补偿决策模型研究，本文利用二叉树模型与MC模型相结合的方法模拟需求的不确定性，将需求保证/限制看成一系列欧式看涨和看跌期权组合成的复合期权，并将其价值模型引入到轨道交通PPP项目资本补偿决策模型中。研究表明：

(1) 需求保证/限制在绝大概率上都会产生价值，政府有必要在轨道交通PPP项目资本补偿决策中考虑其价值。

(2) 考虑需求保证/限制价值能有效降低资本补偿的不稳定性和数量，有利于政府进行资本补偿决策。