非对称组合梁斜拉桥转体施工敏感性分析

邢 云，周 炜，沈毅凯

（上海市建筑科学研究院有限公司，上海市 201108）

0 引言

桥梁转体施工，是一种将桥梁结构在非设计轴线位置浇筑或拼接成形后，利用摩擦系数很小的滑道及合理的转动系统，通过转体使结构就位的施工方法[1，2]。该施工方法能够有效减少对既有交通的影响，是跨越繁忙既有线路的桥梁施工首选，可在斜拉桥、拱桥、刚构桥等多种结构形式中应用[3]。

非对称桥梁进行转体施工时，转体合龙是施工关键控制内容[4，5]。本文以某转体施工的大跨度非对称组合梁斜拉桥为研究对象，进行结构施工过程中主梁支架刚度、斜拉索初始张拉力、梁体配重等施工因素的敏感性分析。研究影响结构受力和线形的因素，为结构顺利转体提供支撑，可为同类桥梁参考。

1 工程背景

1.1 结构概况

本文研究对象为双塔单索面钢混组合梁斜拉桥，桥跨布置为（105+310+155）m，桥型布置如图1所示。

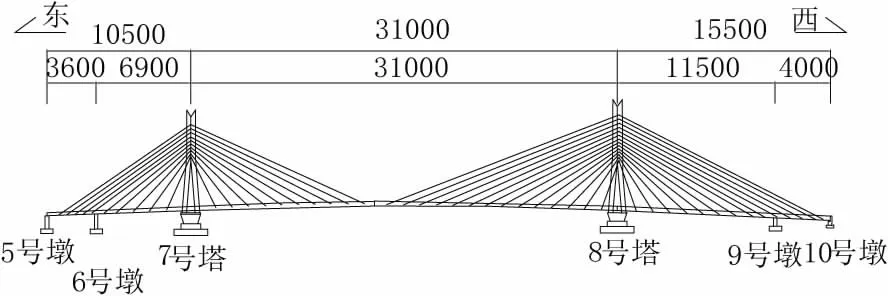
图1 桥梁总体布置图（单位：cm）

斜拉桥主桥结构体系采用半漂浮体系，塔墩固结，塔梁间设置支座体系及液压阻尼器，横向设置抗风支座，两边墩及辅助墩设置竖向支撑。主桥加劲梁采用钢混组合梁，横断面全宽35 m，混凝土桥面板采用C60 预制板，厚28 cm。混凝土桥面板在两边箱范围内设置。斜拉桥主塔设计为纵向“人”字型钢筋混凝土结构，主塔结构由下、中、上塔柱及塔冠部分组成。斜拉索采用中央索面布置，横桥向采用双排索，呈扇形布置，全桥共96 根斜拉索。

1.2 施工方案

由于该桥涉及跨铁路施工，因此采用转体施工技术来实现主梁合龙。主要的施工步骤为：（1）基础、承台、墩身及主塔施工；（2）在完成墩身及塔身的施工之后，顺铁路方向搭设钢管支架；（3）分别在7 号塔和8号塔两侧拼装钢梁、安装预制桥面板，并将预制桥面板与钢梁结合；（4）安装转体段边箱内永久压重块；（5）从桥塔中心向两侧一次安装并张拉斜拉索；（6）主梁脱离支架；（7）安装两端顶升支架及千斤顶支撑体系，通过调节顶升支架顶力，使两侧桥塔和主梁体系保持平衡状态，达到转体状态；（8）转体施工；（9）调整边跨配重，使边跨梁段落于支座上；（10）封固球铰，卸载临时转动系统支撑体系；（11）拼装边跨段；（12）施工完箱内永久压重段，卸除临时压重块；（13）中跨合拢；（14）张拉桥面板纵向钢束；（15）施工桥面铺装及桥面附属设施；（16）索力调整。

2 有限元模型

采用MIDAS CIVIL 建立斜拉桥模型，其中主梁、桥塔均采用梁单元模拟，斜拉索采用索单元模拟。模型整体如图2 所示。全桥共473 个单元，684 个节点，其中主梁单元307 个，桥塔单元70 个，索单元96 个。全桥的边界条件为：斜拉索与桥塔、主梁之间的连接通过刚性连接模拟，支座通过一般支承模拟，桥塔和桥墩底部完全固结。

图2 模型整体示意图

模型共分为31 个施工阶段，其中通过施工阶段联合截面模拟组合梁施工，通过仅受压节点弹性支承模拟主梁施工支架，通过刚性连接模拟塔梁临时固结。

3 支架刚度敏感性分析

斜拉桥主梁施工过程中，转体钢梁部分的拼装以及预制桥面板的浇筑均在支架上进行。研究首先进行施工过程的支架刚度敏感性分析。

取支架刚度为1×105～1×106kN/m，分别得到不同支架刚度下的主梁在支架拆除后的弯矩，如图3所示。由图3 可得，支架刚度对主梁的内力影响很小，这是由于支架解除后的结构体系外部静定，主梁的内力状态主要取决于拉索索力。分析结果与理论吻合。

图3 不同支架刚度下的主梁在支架拆除后的弯矩图（单位：kN/m）

计算不同支架刚度下的主梁在支架拆除后的位移（向上为正，下同），如图4 和表1 所示。由图4 和表1 可知：（1）7 号塔和8 号塔主梁位移随着支架刚度的增大而略有减小。（2）支架刚度对两侧中跨主梁悬臂端位移差影响较小。支架刚度由1×105kN/m提升至1×106kN/m 时，位移差由31.9 mm 减小到30.5 mm，仅减小了1.4 mm。

表1 不同支架刚度下的主梁中跨悬臂端位移

图4 不同支架刚度下的主梁在支架拆除后的位移（单位：mm）

4 初始索力敏感性分析

斜拉桥主梁脱离支架之前，需在支架上进行斜拉索的张拉。斜拉索的初始张拉力至关重要，对主梁脱离支架后的内力和位移都会产生重要影响，需进行相应的敏感性分析。

分别将所有斜拉索的初始张拉力调整为设计初始张拉力的0.95、1.05、1.10（张拉力系数）倍，计算不同初始张拉力下的主梁在脱离支架后的弯矩，如图5 所示。由图5 可知：斜拉索初始张拉力对主梁内力有很大的影响。随着全桥初始索力的增大，两侧主梁中跨及边跨的负弯矩逐渐减小，靠近桥塔处主梁的正弯矩逐渐增大。这表明增大初始索力能够减小主梁跨中处的内力，且同时会增大塔根处主梁的内力。在实际工程中，应合理调节斜拉索的初始张拉力，尽量使主梁内力分布合理、均匀。

图5 不同初始张拉力下主梁在支架拆除后的弯矩图（单位：kN/m）

除了内力之外，斜拉索初始张拉力也会影响主梁的位移。计算不同初始张拉力下的主梁在脱离支架后的位移，如图6 和表2 所示。分析图6 和表2 可得：

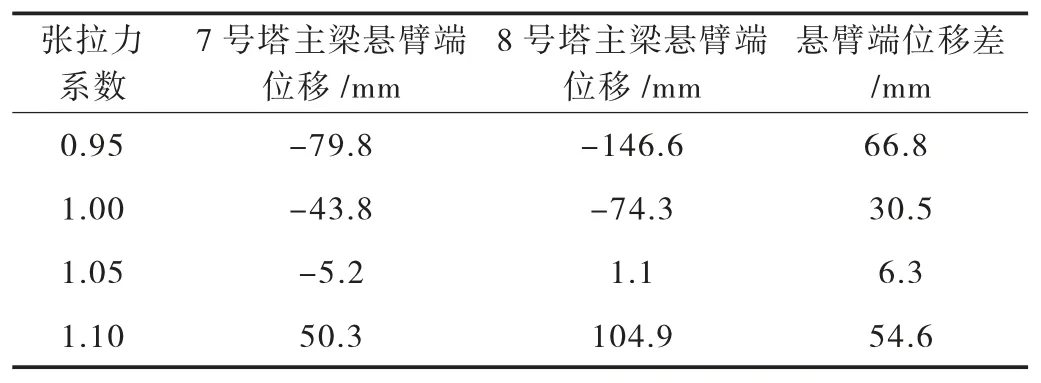
表2 不同初始张拉力下的主梁中跨悬臂端位移

图6 不同初始张拉力下的主梁在支架拆除后的弯矩图（单位：mm）

（1）主梁位移对斜拉索的初始张拉力非常敏感，5%的初始张拉力的改变会使得主梁位移发生成倍数的变化。

（2）初始张拉力的改变会导致主梁脱离支架后的形态发生改变。当初始张拉力较小时，主梁脱离支架后呈现下挠的形态，当初始张拉力较大时，主梁脱离支架后开始呈现上抬的形态。

（3）初始张拉力由设计值的0.95 倍增至1.10 倍的过程中，7 号塔主梁中跨悬臂端位移由-79.8 mm逐渐减小然后增至50.3 mm，8 号塔主梁中跨悬臂端位移由-146.6 mm 逐渐减小然后增至104.9 mm，两侧中跨悬臂端位移差由66.8 mm 先减小然后增至54.6 mm。这表明适当调整初始张拉力可以减小主梁脱离支架后的位移以及两侧中跨悬臂端位移差，初始张拉力过大或过小都对主梁不利。

5 平衡压重敏感性分析

在斜拉桥转体施工之前，需要保证桥塔和主梁体系保持平衡状态，即桥塔底部弯矩接近于0。由于转体前主梁边跨长度小于中跨长度，需要在主梁边跨设置压重以达到平衡状态。边跨压重从主梁悬臂端开始配置，其具体形式如图7 所示，其中q1和q2表示压重单位重量，L1和L2表示压重范围。

图7 压重形式示意图

以塔底弯矩为0 的目标进行不同压重荷载下压重范围的设计：当单位重量较大时，压重范围减小，若单位重量较小，压重范围增大。不同的压重方式对斜拉桥内力和线形产生影响。因此，本节对主梁平衡压重进行敏感性分析。

该桥的设计平衡压重为7 号塔主梁771 kN/m，8号塔主梁340 kN/m。分别计算当压重单位重量为设计值的0.8、1.1、1.2 倍（压重系数）时，为保证平衡所需的压重范围及压重总重，如表3 所示。由表3 可知，压重总重随着压重系数的增大而减小，压重系数由0.8 增至1.2 时，压重总重减小1 010 kN，降幅为4.4%，相对较小。

表3 不同压重系数所需压重范围及压重总重

图8 为不同压重系数下主梁在支架拆除后的弯矩图，由图8 可知：

图8 不同压重系数下的主梁在支架拆除后的弯矩（单位：kN/m）

（1）压重单位重量对边跨主梁内力有较大的影响，而对中跨主梁内力的影响很小。

（2）主梁脱离支架之后，平衡压重会使得边跨主梁靠近悬臂端处产生较大的负弯矩，且最大负弯矩值会随着单位重量的增大而增大；压重系数由0.8 增至1.2 的过程中，7 号塔边跨主梁的最大负弯矩由-16 255 kN/m 增至-51 595 kN/m，8 号塔边跨主梁的最大负弯矩由-24 611 kN/m 增至-34 880 kN/m，变化幅度都很大。这表明增大压重单位重量后，荷载的过度集中对主梁的受力不利，弯矩过大有可能导致结构的损坏，因此在施工中，压重方案应充分考虑主梁的受力情况。

压重在改变主梁内力的同时，必然会对斜拉桥拉索索力产生影响。在拉索初张力相同的情况下，计算不同压重系数下斜拉桥各拉索在支架拆除后的索力，结果如图9 所示。

图9 不同压重系数下支架拆除后的拉索索力（单位：kN）

由图9 可知：

（1）压重单位重量对两侧中跨拉索索力影响很小，但对边跨跨中拉索索力有一定的影响。

（2）随着压重单位重量的增大，边跨外侧几根拉索索力值逐渐增大，而边跨跨中至塔根范围的拉索索力值逐渐减小。

（3）压重单位重量对边跨最外侧拉索索力值影响最大。压重系数由0.8 增至1.2 的过程中，7 号塔边跨最外侧拉索索力值由6 158 kN 增至6 355 kN，8 号塔边跨最外侧拉索索力值由6 541 kN 增至6 674 kN。在转体施工之前，两侧主梁处于悬臂状态，边跨最外侧拉索对主梁内力会产生较大影响。在实际施工调整配重时，需考虑拉索索力的变化。

除此之外，压重对主梁的位移也会产生影响。因此，需要进一步分析平衡压重对斜拉桥主梁位移的影响。计算不同压重系数下主梁在支架拆除后的位移，如图10 和表4 所示。

图10 不同压重系数下的主梁在支架拆除后的位移（单位：mm）

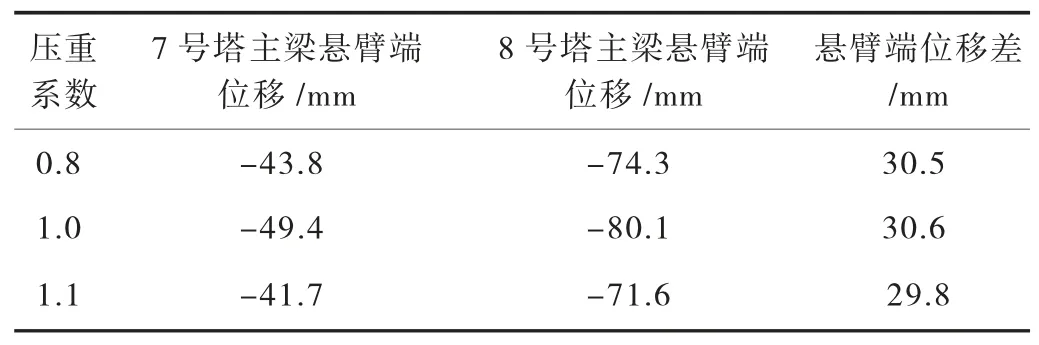
表4 不同压重系数下的主梁中跨悬臂端位移

由图10 和表4 可知：

（1）当压重的单位重量较小时，脱离支架后，两侧边跨悬臂端的位移为正，即主梁存在上翘的趋势；当单位重量增大时，边跨悬臂端位移变为负，且位移随着单位重量的增大而增大。这表明增大单位重量，可以减小主梁跨中悬臂端的下挠，但同时会增大主梁边跨的下挠。

（2）两侧主梁中跨悬臂端的位移均随着单位重量的增大而减小，但单位重量对两侧中跨悬臂端位移差影响较小。当单位重量由设计值的0.8 倍增大至1.2 倍的过程中，两侧中跨悬臂端位移差在29.8～30.6 mm 之间浮动，最大波动差仅0.8 mm。

6 结论

本文采用有限元数值模拟方法，对影响某座非对称组合梁斜拉桥转体合龙结果的因素进行了敏感性分析，得出以下结论：

（1）架设主梁所用的支架刚度对主梁内力影响很小，但对主梁脱离支架后的位移存在影响，较大刚度的支架能够一定程度上抑制主梁的下挠，但支架刚度对两侧中跨主梁悬臂端位移差的影响较小。

（2）斜拉索的初始张拉力对主梁内力和位移均有很大影响。增大初始张拉力能够减小主梁跨中处的弯矩，但同时会增大塔根处主梁的弯矩。随着初始张拉力的增大，主梁脱离支架后的形态由下挠转变为上抬，主梁位移以及两侧中跨悬臂端位移差则呈现先减小后增大的趋势。

（3）增大单位重量可以减小主梁跨中悬臂端的下挠，同时会增大主梁边跨的下挠，但对两侧中跨悬臂端位移差影响较小。

（4）压重单位重量对拉索索力有一定的影响，主梁脱离支架后，压重单位重量对边跨最外侧拉索索力值影响最大。

（5）压重单位重量对边跨主梁内力有较大影响，压重单位重量的增大会显著增大主梁边跨的负弯矩。