基于差分热力计算的空预器温度场和变形研究

沈鹏

（江苏华电句容发电有限公司 江苏句容 212000）

1 背景

回转式空气预热器通过蓄热元件交替经过烟气和空气（一、二次风），实现热量的传递。较管式空预器具有体积小、换热效率高的优点，故被广泛应用在大型火电机组中。回转式空预器整体等效于逆流换热器。烟气侧、空气侧的下部为低温区，在实际运行中，容易发生低温腐蚀、硫酸氢铵结晶堵塞等威胁机组锅炉运行安全的隐患。此外，空预器冷、热端温度存在较大温度差异，造成“蘑菇状”变形，增加了间隙漏风，降低了机组经济性［1］。因此，开展空预器温度分布研究和分析对机组安全经济运行具有重要意义。

因现场条件限制，不易实现空预器温度场的全面测量。国内外学者通常采用数值模拟方法开展研究，主要路径包括数值模拟和热力计算迭代方法。数值模拟方面，Armin 等［2］对二分仓回转式空预器进行CFD 三维数值模拟，分析了蓄热元件材料、工质流速和温度对换热效率的影响；Bostjan 等［3］对三分仓回转式空预器采用Fluent 软件进行工质流场的模拟；宋彦美［4］将空预器单元作为研究对象，交替改变边界条件开展数值模拟，获得了工质和蓄热元件的温度分布规律。侯益铭等［5］在模拟和试验基础上，分析了四分仓和五分仓空预器进出口温度、换热面特性对温度场分布的影响。另外，高建强等［6］对不同形式的蓄热板元件进行数值模拟，确定较优的蓄热元件板型。热力计算方面，阎维平等［7］建立三分仓空气预热器换热计算模型，提出迭代求解方程和计算流程，能够较好地计算出热端与冷端受热面交界截面的平均温度；陈欢等［8］以1 000 MW 锅炉空预器为例，建立三分仓微元数学模型，获得空预器内蓄热元件的温度，为低温腐蚀提供参考。周俊虎等［9］定义传热系数和温压，提出不涉及转子本身热参数的计算方法用于积灰状态的在线监测。类似的，冷伟等［10］、郑凯等［11］均对空预器热力计算方法提出改进，有效提高计算精度。

尽管已对空预器温度场研究开展较多工作，但缺乏不同计算方法间的比较，且空预器温度分布与转子位移变化间关系的研究不够完善。因此，本文采用热力性能计算的方法对空预器的温度分布进行求解，得到工质和金属的温度分布规律，并对空预器转子位移变化规律进行研究，为回转式空预器密封系统的设计提供指导和参考。

2 空气预热器数值模型

尽管空预器内单个蓄热板发生非稳态换热，但当蓄热板厚度足够小时，可认为是稳态换热。因此，本文在对空预器温度场进行热力计算时，将空预器整个蓄热元件视为稳态换热。此时，忽略蓄热元件（转子）径向温差和辐射换热，将空预器沿转动方向展开，即将三维模型简化为二维模型，见图1。将模型离散后，建立工质与蓄热元件间的热平衡方程，并采用高斯-赛德尔迭代算法进行求解。

图1 三分仓回转式空预器简化模型

2.1 传热计算数学模型

空预器工作过程中，金属蓄热元件与工质间遵循热量守恒。以蓄热元件与空气换热为例，蓄热元件释放的热量计算如式（1）。

式中：cw为蓄热元件的比热，kJ/（kg·K）；mw为蓄热元件质量，kg；n 为空预器转动速度，r/min；tw为蓄热元件壁面温度，K；tf为空气温度，K。

空气吸收的热量计算如式（2）。

式中：ca为空气的比热，kJ/（kg·K）；ma为烟气质量流量，kg/s；ha为空气与蓄热元件的对流换热系数，W/（m2·K）；A 为蓄热元件换热面积，m2。

对图1 空预器简化模型沿轴向和周向分别划分为m 行和n 列，即网格数量为m×n 个网格。每个网格域内工质（烟气、空气）和蓄热元件的温度等于对应的进出口平均温度。以第i 行j列处的网格为例，蓄热元件与空气间的换热方程离散为公式（3）和公式（4）。

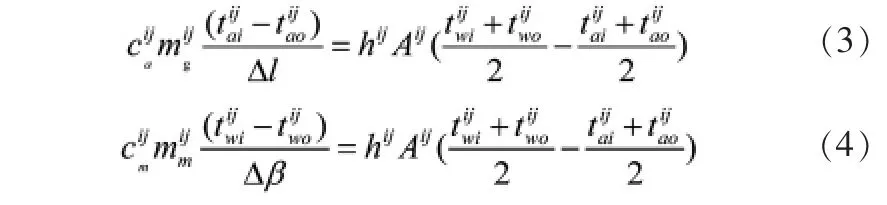
式中：上标ij 表示第i 行第j 列处的网格，下标gi、go表示该网格处的空气进、出口，下标wi、wo表示蓄热元件进出口；Δl 为网格高度，m；Δβ 为网格角度，（°）。

对以上两式联立求解，获得第i 行j 列网格出口处的空气温度和蓄热元件温度的计算公式（5）和（6）。

同理，烟气与蓄热元件间的换热方程也可离散获得。

2.2 模型求解

通常，工质比热容、换热系数与温度相关，但在每个网格内，工质温度与蓄热元件温度变化很小，故可采用定性温度来确定。根据2.1 节建立的换热模型和离散化网格，进行空预器温度分布的求解，求解过程见图2。

图2 迭代计算流程图

首先，输入工质进口温度和流量，并充分考虑漏风影响，对各工质进口温度进行修正；然后，假设空预器轴向方向上第1 列网格的进口蓄热元件壁温，并根据式（5）和式（6）求得该列网格的出口流体温度和壁面温度，继续下一列网格出口温度的计算。由空预器工作过程可知，蓄热元件由一次风侧再次进入烟气侧时，第n 列（图2 中最右侧）蓄热元件的壁温与第1列（图2 中最左侧）蓄热元件的壁温相等，因此将其作为迭代计算的终止条件。即两者的绝对温差小于收敛条件，迭代计算结束。否则，将第n 列壁温赋值给第1 列壁温，继续迭代计算。

2.3 空预器参数

本文以某600 MW 锅炉的空气预热器作为模拟对象，其设计参数和结构设计参数见表1 和表2。

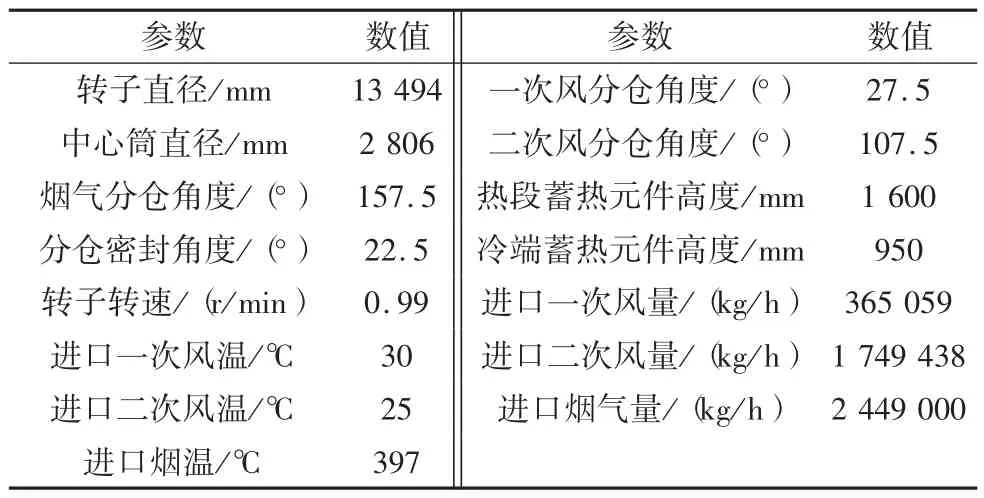
表1 某600 MW 机组空预器设计与结构参数

表2 蓄热元件结构设计参数

3 计算结果分析

本文空预器模型离散为2 240 个网格，即轴向高度方向上划分为70 行，轴向方向上划分为32 列。其中：烟气侧划分为16 列，二次风侧划分为11 列，一次风侧划分为5 列。通过高斯—赛德尔迭代计算，获得空预器工质温度云图和蓄热元件温度云图（见图3 和图4）。由图3 和图4 可看出空预器的工质温度分布在烟气侧和空气侧出现间断，但蓄热元件的温度分布则成呈现为连续性。

图3 工质温度分布云图

图4 金属温度分布云图

图5 为不同行数和列数位置工质温度变化图。由图5（a）可看出在烟气分仓内，烟气温度逐渐升高，而空气温度逐渐降低，且行号越大（越靠近冷端），该变化趋势越明显。图5（b）表明不同列位置的工质温度随与热端距离的增加而逐渐降低，烟气分区内第16 列烟气温度高于第1 列温度，而二次风分区第17 列空气温度高于第27 列网格处空气温度。这与工质与蓄热元件间温差引起的对流换热变化有关。

图5 不同行数/列数位置工质温度变化

图6 为不同行数或列数位置蓄热元件温度分布图。由图6（a）可看出随着周向列数的增加，空预器蓄热元件温度先增加后逐渐减少，该变化趋势在第44 行时最为明显，原因是此位置为空预器热端出口，存在较大的温差变化。图6（b）则表明，随着距离空预器顶部位置距离的增加，蓄热元件温度逐渐降低，这与烟气的温度降低有关。图6（b）中蓄热元件温度变化还可以表明在热段进入冷段的交界面上发生了蓄热元件温度的跳跃，如第16 行、第17 行温度下降，而第1、第27、第28和第32 行则出现温度上升。这与不同蓄热元件的换热性能有关。热段蓄热元件的换热系数高，其与工质间热量交换能力强，蓄热元件温度的变化较明显；而冷段蓄热元件通常采用镀搪瓷的碳素钢（预防低温腐蚀），换热系数减小，换热性能变差。因此在烟气侧，烟气在冷段加热蓄热元件能力弱于热段，对应的冷段金属温度低于热段金属温度。同理，空气在冷段冷却蓄热元件的能力弱于热段，造成冷热段交界面上温度的骤升。

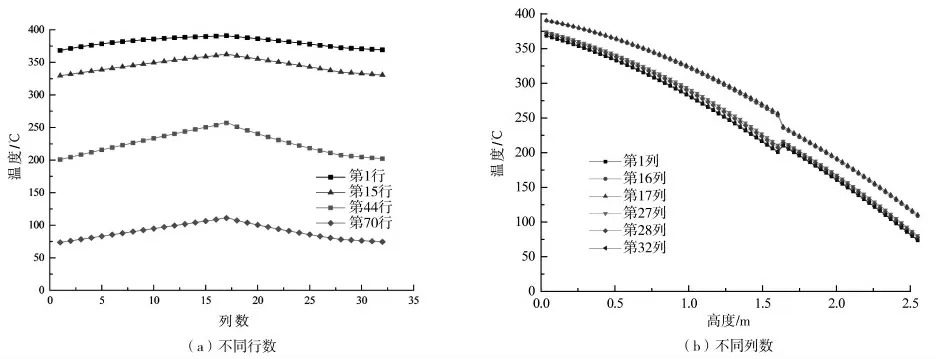
图6 不同行数/列数位置蓄热元件温度变化

由表3 可看出，基于有限差分的热力计算方法所获得的烟气温度、空气（一、二次风）温度与设计值比较接近，热力计算方法具有更高的误差精度，平均相对误差为3.78%。表明该计算方法能够较为准确地进行温度场计算。

表3 空预器出口温度温度比较

4 空预器冷热端位移量计算

回转式空预器漏风主要包括径向、轴向和环向漏风三部分，且径向漏风占较大部分。为减小该漏风，需调整转子隔板与密封板的间隙。因此，探索空预器转子的位移变化规律具有重要意义。目前，对于空预器转子的位移变化，张义宾等［12-16］获得简化后的经验关联式（7）。

式中：h 为转子位移量，mm；t2为空预器热端温度，℃；t1为空预器冷端温度，取温差最大区域的冷端温度，℃；t0为环境温度，取20 ℃；1、2 为冷端和热端温度对应的材料线膨胀系数，10-6/℃；R 为转子半径，m；H 换热元件高度，mm。

实际运行中，为预防硫酸氢铵结晶造成的腐蚀作用，空预器冷端多采用碳钢表面镀搪瓷的方式，因材料线性膨胀系数存在不同，如直接采用经验公式（7）进行转子位移计算，则存在较大误差，因此考虑单独计算转子热段位移和冷端位移变化量，对空预器转子位移经验公式进行改进，获得公式（8）。

式中：下标r 表示空预器热端，下标l 表示空预器冷端，下标1、2 表示入口位置和出口位置；Δt 表示冷热端温差，℃；α 表示转子材料线膨胀系数，10-6/℃。

将热力计算方法所获得的空预器转子热段、冷段的进出口位置的温度，以及各位置膨胀系数、转子高度等带入公式（8），计算出转子位移变化量为32.41 mm。这与实际运行中空预器转子的位移变化量（34.65 mm）相比，两者的相对误差为-6.48%，表明本文所提出的热力计算方法可用于空预器转子位移变化的预测。

5 结论

通过有限差分的热力计算方法，本文获得回转式空预器工质和蓄热元件的温度分布，比较与设计工况下的工质出口温度，确定热力计算方法能够较为准确地对空预器温度场进行计算，平均绝对误差为3.78%。同时提出了考虑冷、热段材质区别的转子位移改进公式（相对误差为-6.48%），为回转式空预器密封系统的设计提供指导和参考。