基于PSO优化的SVM在心脏病分类上的应用

曹嘉嘉 严圆 陈益 尹玲 张斐

(1.东莞理工学院 计算机科学与技术学院， 广东东莞 523808；2.纽卡斯尔大学 工程学院，英国纽卡斯尔 NE1 7RU；3.东莞理工学院 机械工程学院，广东东莞 523808)

研究表明，我国有大量心血管疾病患者，其中心脏病患者占据多数，并且我国心血管疾病的患病率和死亡率呈上升趋势[1-2]，心血管疾病已成为我国居民的主要死亡方式[3]。心脏病的及早诊断，对治疗非常重要。但是由于病人繁多，医生诊断会非常的耗时。随着人工智能在医疗应用上的崛起，心脏病辅助诊断的研究成果显著，文献[4]利用了贝叶斯优化算法对随机森林分类模型进行参数寻优，而后将优化的模型应用到心脏病分类。文献[5]通过自适应遗传算法选择数据特征，而后使用人工蜂群算法优化ELM隐层输入权值和偏置，改善了ELM分类精度不高的缺陷。虽然心脏病的辅助诊断取得了一定进展，但是由于数据样本量少，学者们仍需探寻一个性能优异的小样本分类器。

SVM由Vapnik等人[6]提出了一种基于统计学的有监督机器学习方法，最早被用于解决二分类问题。与深度学习方法相比，SVM可以避免过拟合、陷入局部最优和低收敛性的问题。最小化的经验风险和结构风险保证了SVM的高泛化能力。而且它在小样本的处理上表现良好，刚好满足了目前数据不足的问题。然而，SVM的性能取决于两个重要的参数：(1)惩罚参数C，(2)核函数及它的参数。分类边界的最大化和误差最小化之间的平衡受惩罚参数的影响。而核函数的参数决定了输入特征从低维空间到高维空间的映射质量。在实践中，这两个参数的设置往往依靠个人经验，个人经验的优劣决定了SVM的性能，这给SVM的性能带来了不确定性。

粒子群优化算法由 Eberhart 和 Kennedy 于 1995 年提出[7]了一种模仿昆虫、鸟类等集体觅食行为的随机并行优化算法。粒子群优化算法的目标函数可以是不可微、不连续的，并且它具有收敛速度快、算法简单、易于实现等优点，所以经常被用于各种优化问题[8-9]。

基于上述分析，本文提出了一种基于粒子群优化支持向量机(PSO-SVM)的心脏病辅助诊断算法，该算法使用粒子群优化算法自适应选择支持向量机的参数，在Cleveland heart disease数据集上进行算法验证，实现了PSO-SVM模型在心脏病分类任务中的应用。另外还比较了所提方法在不同核函数下心脏病分类的性能，最终实验结果表明多项式核函数在本数据集上表现最佳，心脏病分类准确率最高可达到88%。

1 PSO-SVM算法

1.1 支持向量机

SVM是一种基于统计学理论的有监督机器学习方法，常用于分类和回归。通过搜索最小结构风险，可以提高SVM分类器的泛化能力和最小化经验风险。因此，它在样本量较小的情况下也能展现出良好的分类性能。SVM的核心思想是找到一个可以分离不同类别数据的超平面，并最大化支持向量到超平面的间距。

假设存在数据集D={(x1,y1),(x2,y2),…,(xm,ym)},yi∈{-1,+1} ；其中xi是输入数据，是一个N维的向量；yi是类标签。在样本空间中，超平面的定义如下：

ωTx+b=0 ，

(1)

其中，ω=(ω1;ω2;…;ωd)是确定超平面的法向因子；b是位移项用于确定超平面与原点间的距离。显然，超平面由ω和b共同确定。

假设超平面(ω,b)可以直接将数据分类，则有：

(2)

能够使式(2)中等号成立的输入数据称作“支持向量”。当两个异类支持向量到超平面的距离和最大时，该超平面即是所搜索的目标平面。而这个距离被称为“最大边距”，定义如下：

s.t.yi(ωTxi+b)≥1 ,i=1,2,…,m.

(3)

这意味着SVM的基本工作原理就是找到能够满足约束条件的ω,b，使得“最大边距”最大化。

使用拉格朗日乘子法，以及引入核函数，式(3)的对偶问题表示如下：

(4)

此时超平面模型表示成：

(5)

其中函数k(.,.)表示“核函数”，用以实现将样本从原始特征空间映射到更高维的特征空间。核函数的种类如下所示：

•d次多项式核：k(xi,xj)=(+c)d.

在现实中，很难找到一个合适的核函数使得训练样本能够在特征空间中线性分离。因此，需要加入松弛变量ξi来放松线性SVM的约束，其中ξi表示第i个训练模式与对应的边距超平面之间的距离，并且它应该最小化。最终SVM的优化目标定义如下。

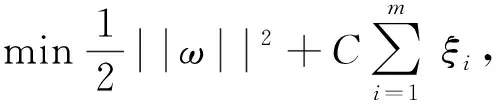
(6)

式中，C是一个大于0的常数，表示为对错误样本的惩罚程度。

实验中SVM借助工具箱 LIBSVM[10]来实现，LIBSVM由Chang等人开发了一个可用于支持向量分类，回归的集成软件。

1.2 粒子群优化算法

粒子是一种基于种群的计算技术，它用以模拟鸟群中的个体(粒子)[11]。粒子群优化算法(PSO)首先在可行解空间中初始化一群粒子，每个粒子代表极值优化问题的一个潜在最优解。该粒子的特征由三个指标表示：位置、速度和适应值。在每次迭代中，粒子通过个体极值和群体极值来更新自己的速度和位置。更新公式如下：

(7)

其中，i=1,2,…,m，代表第i个粒子；k=1,2,…,K,表示维度；V是粒子的速度，同时对当前速度加上两个修正：(1)该个体与当前路径中最优个体的差异；(2)该个体与群体最优值的偏差； 是惯性因子；和是加速系数，和是在[0,1]之间随机数字。X是位置，是上一个位置与当前速度的加和。实验中采用的是标准粒子群算法(PSO 2011)，下文简称PSO。

1.3 PSO-SVM建模

在使用SVM进行心脏病分类时，需要优化SVM模型中惩罚系数C以及所选定的核函数的参数。将采用PSO算法优化SVM的超参数，使SVM模型在心脏病预测上达到理想的分类效果。同时，为了选出最适合本模型的核函数，实验对三种核函数都进行了测试，最后根据实验结果择优。

算法流程如图 1所示，具体的处理步骤为：

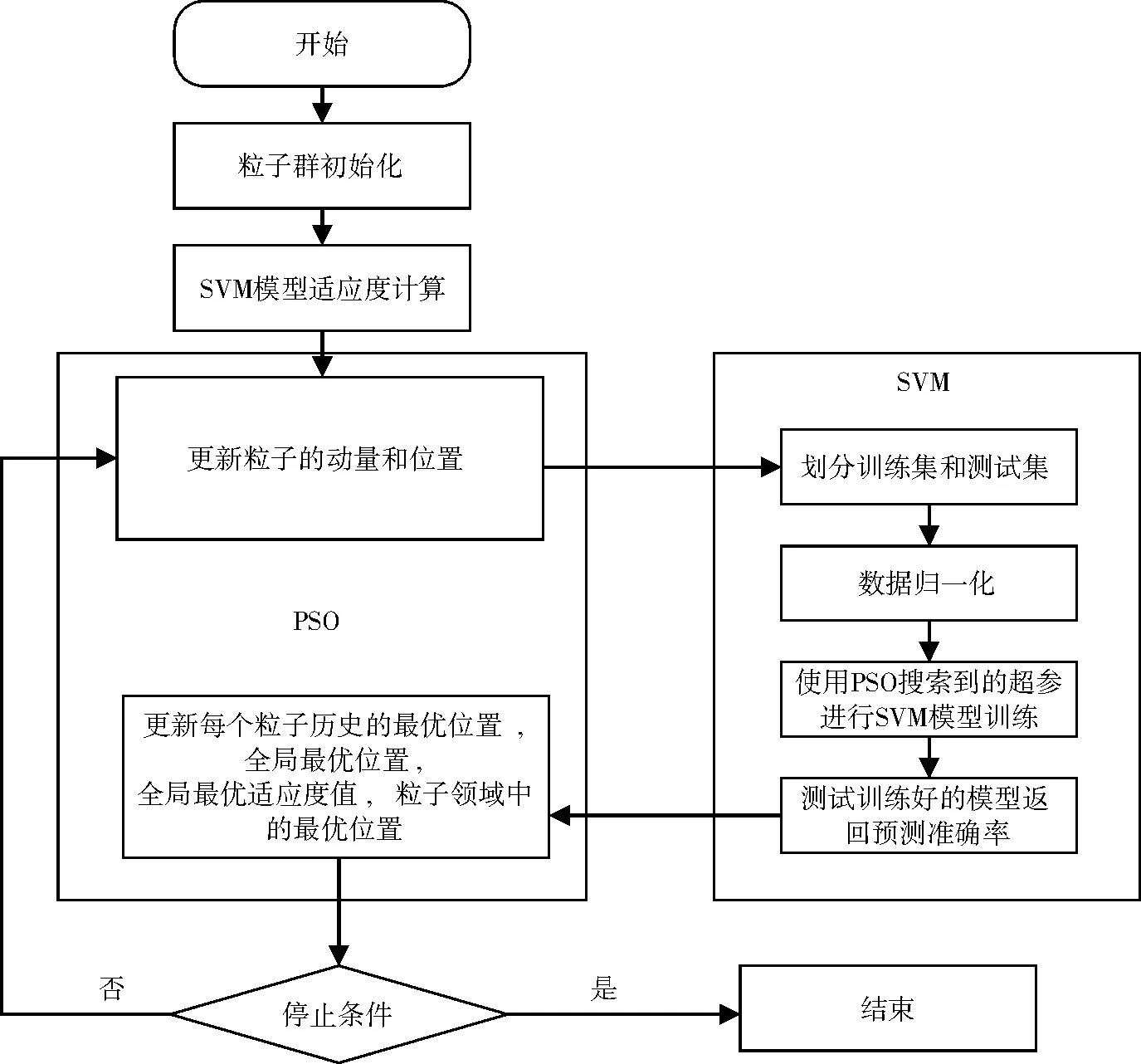
图1 PSO-SVM算法流程图

1)初始化粒子种群。对于不同的核函数，粒子种群大小都初始化为30，算法迭代次数为10 000次。对于RBF核函数需要优化两个参数，分别是c, gamma；对于多项式核函数需要优化4个参数，分别是c、gamma、r和d;对于sigmoid核函数，需要优化三个参数，分别是c、gamma和r,具体的取值范围见表3。随机初始化粒子的初速度和初始位置。

2)计算适应度值。在实验中，将训练好的模型在测试集的分类准确率作为PSO的适应度值，并将每个个体的初始适应度值作为个体的最优适应值，将种群初始适应值中最优的适应度值作为全局最优适应值。

3)在给定的约束内，按照式(7)更新粒子的速度和位置。

4)根据更新的位置计算适应度值。

5)更新个体最优和全局最优。如果当前个体适应度值优于之前个体最优，则将当前适应度值设为最优个体适应值，对应的位置设为个体最优位置。如果当前粒子适应度值要优于全局最优适应值，则将当前粒子适应度值设为全局最优适应度值，对应的位置设为全局最优位置。

6)终止判断。如果满足终止条件，算法停止并返回最优的参数和准确率。否则重复过程3)到5)。

2 数据与实验环境

2.1 心脏病数据集

研究采用的心脏病数据集来源于UCI Repository[12]。该数据集包含了4个子数据集，本文仅使用其中的Cleveland心脏病子集，以下简称其为心脏病数据集。该数据集共有303个样本，其中164个是没有患心脏病的，剩下的139个是患有心脏病的。每个样本都包含76个属性，但与大多数已发表的研究一样，仅使用了其中的14个属性。研究的重点是简单地区分患病(值 1、2、3、4)和不患病(值 0)。表1是心脏病数据集各属性的取值范围。表 2是对每个属性的详细说明。

表2 心脏病数据集各属性说明

2.2 数据预处理

由于心脏病数据嘈杂(如表 1所示)，14个属性值都在不同的范围内，且存在个别属性值缺失的数据，所以在模型训练之前需要对数据进行预处理。首先，将数据处理成SVM支持的格式，将值在(1,2,3,4)中的数据的预测属性设置为1，表示存在疾病。第二，删除属性值缺失的样本。第三，数据归一化处理。研究需要将数据特征值缩放到 [0,1] 之间，以避免较大数值范围内的特征主导较小范围内的特征，使用最小-最大缩放原则,其表达如下

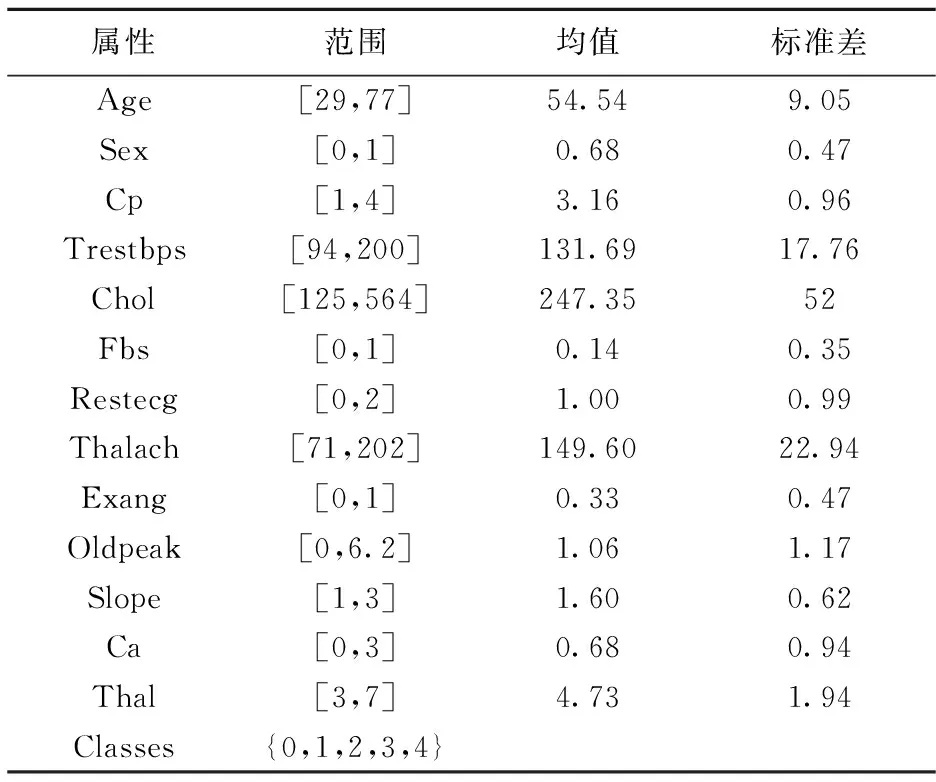
表1 心脏病数据集属性取值范围

(8)

其中v是原始矩阵，min是整个矩阵的最小特征值。Max是整个矩阵的最大特征值,v′是缩放后的值。

将预处理后的数据进行划分，前200条作为训练集，后97条作为测试集。将划分好的数据导入到PSO-SVM模型中，算法的初始参数设置如表3所示，算法迭代10 000次，重复了18次实验，以18次实验的平均准确率作为算法的准确率。两种算法在不同核函数下对心脏病预测的准确率如表4所示。从表4可以看出，PSO-SVM 的分类准确率高于支持向量机，但提升幅度不大。为了进一步提高预测准确性，需要进一步进行数据处理。

表3 PSO-SVM初始化参数列表

表4 PSO-SVM与SVM使用不同核函数的预测准确率比较(18次重复实验的均值) %

为确定每个属性的重要性，实验尝试分别删除每个属性，再使用上面PSO-SVM 找到的最优参数来训练SVM模型(选择的内核是 RBF)，随后观察不同属性对分类器的贡献。属性被删除后所训练的模型的分类准确率如表5。如果删除该属性后，准确率反而提高，则认为该属性阻碍分类。相反，则认为这个属性是必要的。观察表5，与删除前82.47%的准确率相比，删除属性Restecg、Exang后的准确率有所提高。因此，可以假设可以删除属性 Restecg、Exang。

表5 SVM在删除不同属性后的心脏病数据集上的分类准确率 %

为进一步确定哪一个属性适合删除，设置消融实验，分别使用删除Restecg、Exang、Restecg&Exang属性后的数据训练和测试PSO-SVM模型。最后，与移除该属性之前的模型预测准确率进行比较。结果如图2所示，从图2中可以看出，单独删除属性 Exang 后准确率提高最大，最终决定删除属性Exang。

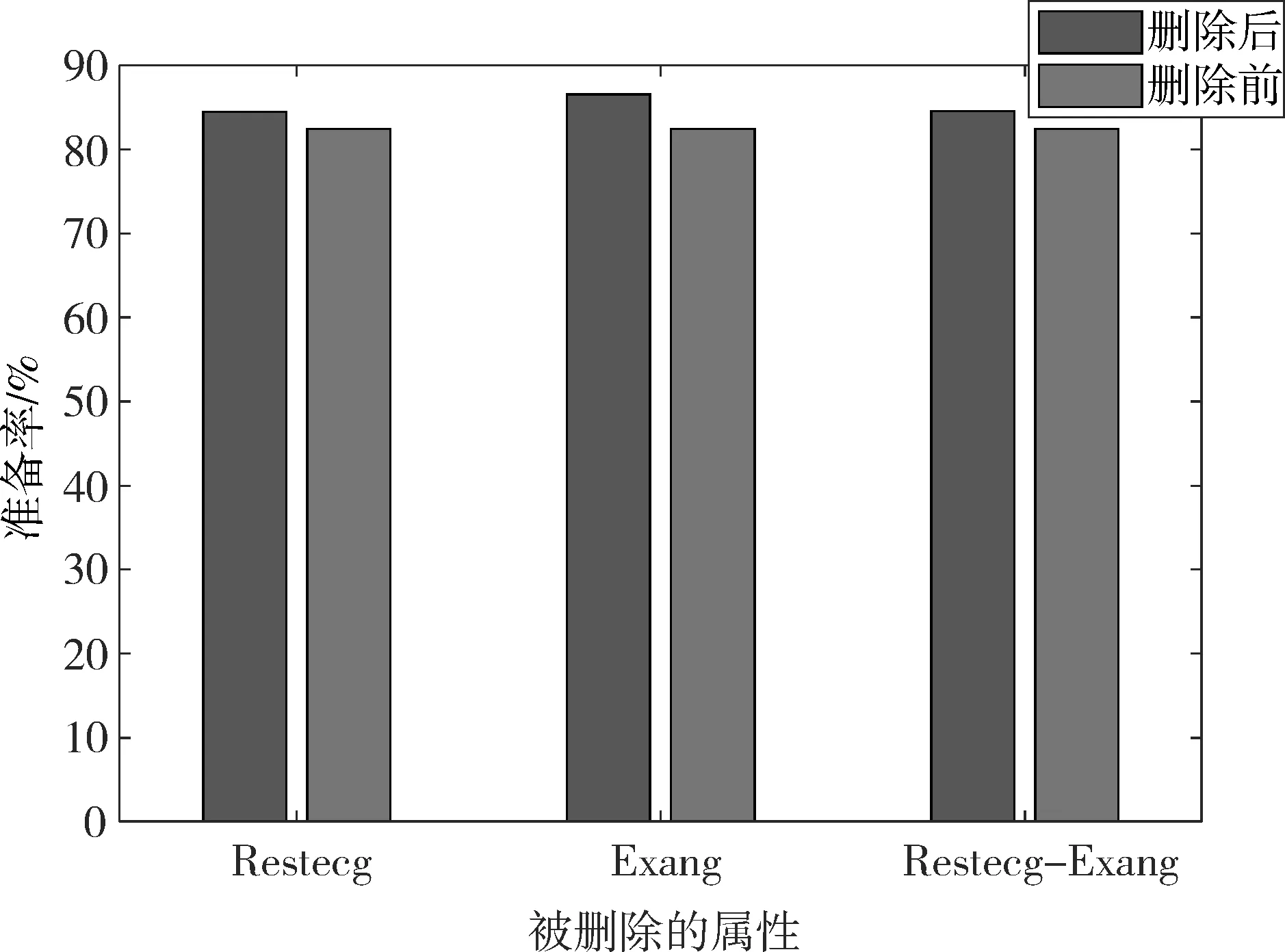
图2 PSO-SVM分别在删除Restecg，Exang，Restecg和Exang后的心脏病数据集上的分类准确率

2.3 实验环境

实验使用的计算机配置如表6。选择MATLAB R2018a为开发工具。LIBSVM 3.24工具箱用以实现SVM功能。所选的优化算法为标准粒子群优化算法2011。PSO-SVM算法停止条件为达到预设的最大迭代数。实验中，最佳解决方案的最大重复次数为10 000。

表6 实验使用的计算机配置表

3 实验仿真与结果分析

经数据处理后，最终样本量为297条，数据集中两类样本的分布如表 7所示(两类样本分布均匀)。将前200条作为训练数据，后97条作为测试数据，使用PSO-SVM算法在处理后的数据集上学习和分类，仅区分患病或者不患病，算法的初始化参数如表3。独立重复20次实验，最终PSO-SVM算法的平均分类准确率以及寻优到的SVM参数如表8。为证明PSO-SVM算法的有效性，将算法和SVM进行比较(如图3)，是使用不同核函数的 PSO-SVM 的平均精度和使用不同内核的SVM的精度比较。

表7 处理后心脏病数据集样本分布

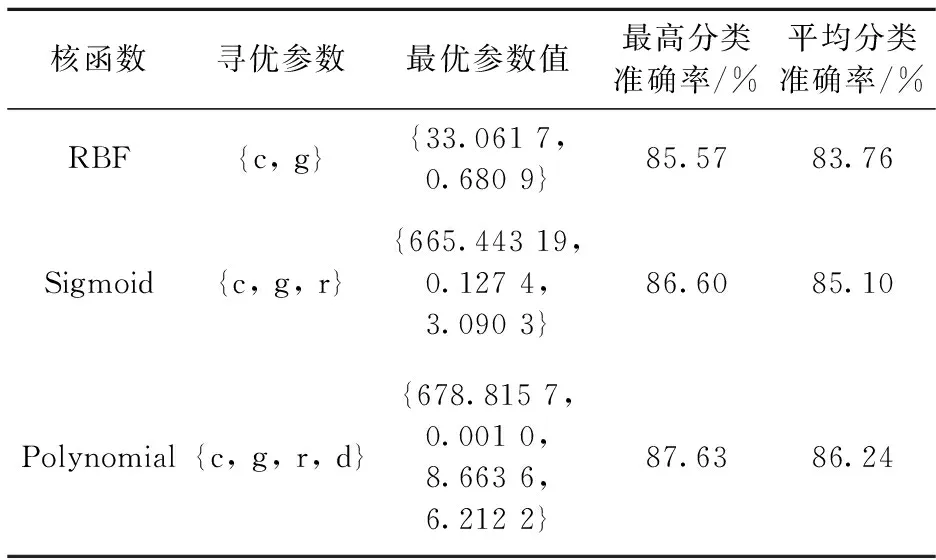
表8 模型寻优参数及模型平均分类准确率 (独立重复实验20次)

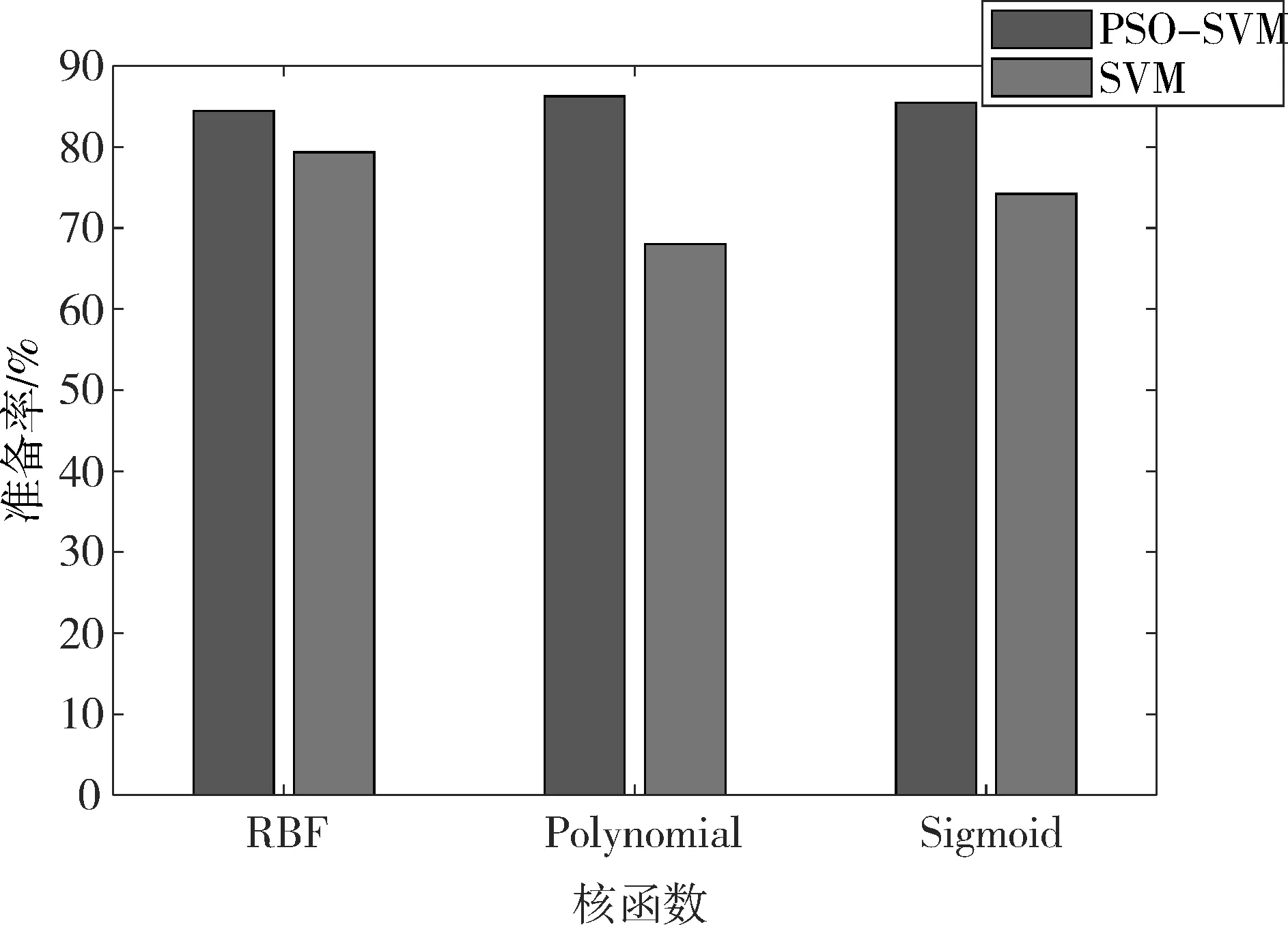
图3 不同核函数的PSO-SVM和SVM在心脏病分类上的准确率比较

结合表8和图3可以看出，无论使用哪种核函数的 PSO-SVM，在心脏病数据集中的分类准确率都高于传统SVM。而且使用Polynomial核函数的PSO-SVM的平均分类准确率最高，其最高分类准确率可达到87.63%，可以推出Polynomial为心脏病分类模型的最合适核函数。

另外为了评估所提算法的性能，将使用不同核函数的PSO-SVM各自运行50次，分别将每次的适应度曲线描绘在同一图中(如图4)，从图4中可以观察到，使用PSO-SVM 算法时，无论选择哪个核，粒子都会快速收敛，并且越来越接近最优解。由此推断，本文所提的PSO-SVM 是可行且高效的。

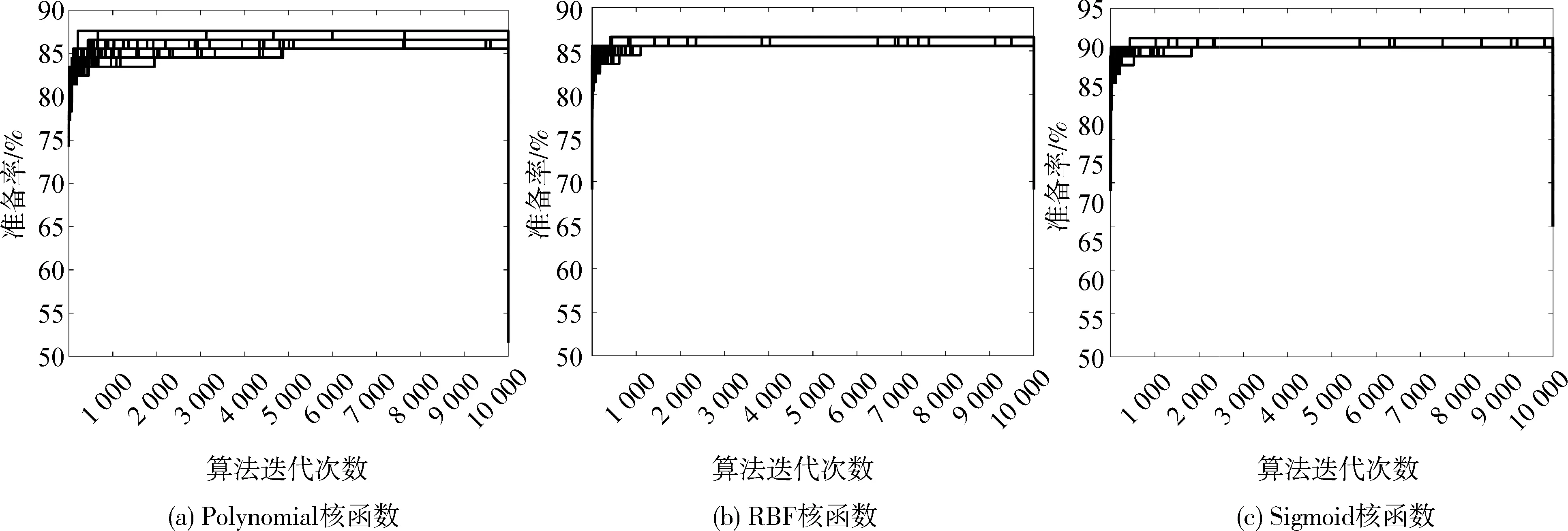
图4 三种核函数对应的PSO-SVM执行50次的适应度曲线

为了评估算法的稳定性，将使用不同核函数的PSO-SVM各自运行45次，并将每次的最优适应度值(最佳准确率)描绘在同一图中(如图5)，从图5可以看出，本研究找到的最优解上下波动，但始终在一个范围内波动且波动不大。而且最小值要高于SVM中测得的值。即PSO-SVM找到的值要么是最优的，要么是次优的，但均比SVM好，综上可以推断该算法是相对稳定的。

图5 不同核函数下的PSO-SVM算法独立运行45次的最佳准确率曲线

4 结语

笔者开发了一种基于PSO-SVM的心脏病预测模型。模型使用PSO选择SVM的超参数，然后使用心脏病训练集训练模型，最后使用测试集测试了模型的性能。同时还比较了不同核函数下PSO-SVM的分类性能，以期找到最适合数据集的核函数。最后对比了PSO-SVM与传统SVM在心脏病上的分类准确率，实验结果表明PSO-SVM的准确率有所提高。本研究的贡献有两个方面，首先，这项工作解决了SVM参数的选择问题，该方法无需人为设置SVM超参数，为没有机器学习经验但想使用SVM的人群带来了便利；其次，通过对不同核函数的比较，发现多项式核函数最适合此心脏病数据集，最高分类准确率为 88%。

研究的下一步将使用改进的PSO算法来选择SVM的参数或者开发一个不仅可以选择SVM的参数还可以选择最合适的核函数的算法[13]。