Collision enhanced hyper-damping in nonlinear elastic metamaterial

Miao Yu(于淼) Xin Fang(方鑫) Dianlong Yu(郁殿龙) Jihong Wen(温激鸿) and Li Cheng(成利)

1Laboratory of Science and Technology on Integrated Logistics Support,National University of Defense Technology,Changsha 410073,China

2Department of Mechanical Engineering,Hong Kong Polytechnic University,Hong Kong,China

Keywords: nonlinear elastic metamaterial,hyper-damping,vibration suppression

1. Introduction

In the last decade,elastic metamaterials have shown great promise for elastic wave manipulation,[1–4]which are mainly limited to linear elastic metamaterials. In linear metamaterials, bandgaps arising from local resonances and Bragg scattering are of great significance for vibration reduction.[5,6]Limited by the mass and the size in practice, commonly achieved low-frequency bandgaps usually exhibit narrowband feature. Attaching different resonators[7–10]or amplifying the inertia[11–14]can broaden the bandgaps to a certain extent. Another important effect for vibration reduction and wave energy absorption in linear metamaterials is the hyper damping induced by local resonances.[15–17]This means that a material processes superior dissipation ability as compared with other materials with the same damping composition and equivalent static properties.[18]This is generally achieved by composite/architected materials or metamaterials. The hyperdamping effect in linear elastic metamaterials has been studied in a series of works by using different metamaterial configurations. Damping leads to broader vibration suppression,at the expenses of compromising the bandgaps. At present,realizing low-frequency and broadband bandgaps and simultaneous hyper damping remains a challenge in linear elastic metamaterials.[19,20]

Elastic metamaterials with strong nonlinearity, i.e., nonlinear elastic metamaterials, can give rise to extraordinary physical phenomena,which can be exploited for elastic wave manipulation and vibration suppression.[21–24]Therefore,nonlinear elastic metamaterial becomes a hot topic in recent years.Due to the high-order harmonics, wave energy in nonlinear elastic metamaterials can be transferred from low to higher frequencies.[21,22]Except for the conventional band gaps similar to linear metamaterials, a region near 1/2-subharmonic in nonlinear elastic metamaterials can widen the frequency range of vibration attenuation.[23,24]Nonlinear effects can produce tunable and adaptive band gaps.[25–30]The amplitudes of nonlinear resonances in chaotic bands of nonlinear elastic metamaterials can be significantly suppressed, which greatly expands the bandwidth of suppressed waves.[31–37]However,the desired nonlinear effect requires relatively large incident amplitude,whilst achievable nonlinear coefficient in practical structures is usually limited. Moreover,vibration transmission in nonlinear metamaterials remains high when the incident amplitude becomes very large.[37]Damping and even hyperdamping effect may alleviate these challenges to improve the performance of nonlinear metamaterials. However, ways to achieve hyper damping in nonlinear elastic metamaterials are lacking and,even if achievable,the mechanisms underpinning the physical process remains unclear.

As well known, a viscous damper connecting two elements produces a damping forceFd, which is proportional to the relative velocityvbetween the two objects, namelyFd=cv,wherevis the gradient of relative displacement. For a given damping coefficientc, introducing an abrupt change of displacement can increasevandFdto produce large energy dissipation because the“abrupt change”leads to the infinite gradient in mathematics. A dedicated way for producing such an abrupt change is through the collision between the objects,which subsequently generates strong nonlinear damping forces. Capitalizing on this concept, we design a nonlinear elastic metamaterial by combining the damping and collision in a meta-cell,which can induce robust hyper damping as required. This paper aims at investigating the feasibility of such design, tackling a few important aspects relating to its materialization and shedding lights on the underlying mechanisms. More specifically, we numerically study the damping efficiency and vibration transmission of different metamaterial models. The influences of amplitude and damping coefficient are analyzed to find a robust design scheme. This paper offers a novel way for conceiving nonlinear elastic metamaterials which entail effective vibration suppression.

2. Model and methods

2.1. Metamaterial models

We consider a finite one-dimensional metamaterial model shown in Fig.1.Each meta-cell consists of a primary massm0,which is coupled to a resonator. Three kinds of coupling arrangement inside the meta-cell are considered, as shown in Figs. 1(b)–1(d). The damping in the primary chain is neglected. As a result, damping only comes from the motion inside meta-cells.

Fig.1. Model of elastic metamaterial and its constituent meta-cell. (a)Elastic metamaterial model;(b)linear meta-cell;(c)meta-cell with bilateral collision;(d)sandwich-collision meta-cell.

The first coupling scenario depicted in Fig.1(b)leads to a linear metamaterial. The equation of motion in thenthcell writes

whereunandynare the displacement of the primary massm0and the local resonatorm1in thenthcell, respectively,k0is the stiffness of the spring between neighborm0,andk1is the linear stiffness betweenm0andm1. Here,a bilateral damping is introduced betweenm0andm1,andc0denotes the damping coefficient.

In the second model shown in Fig.1(c),in addition to the linear stiffnessk1, the bilateral collision ofm1is introduced.According to the Hertz contact theory,the collision force takes the form ofkNδ3/2,wherekNis the collision stiffness. Therefore,expressions of forcesF1andF2labeled in Fig.1(c)write

The third model shown in Fig.1(d)also considers the collision nonlinearity, but the massm1is split into two identical resonators,m2=m1/2. Besides the nonlinear coupling betweenm2andm0,the damping and linear coupling between the two massesm2are also considered. We will show later that this tiny change leads to a significant improvement of the performance. The resulting metamaterial is referred to as sandwichcollision metamaterial because the damping between the twom2behaves like a sandwich cake.Similar to the second model,the equations of motion in thenthcell of the third metamaterial write

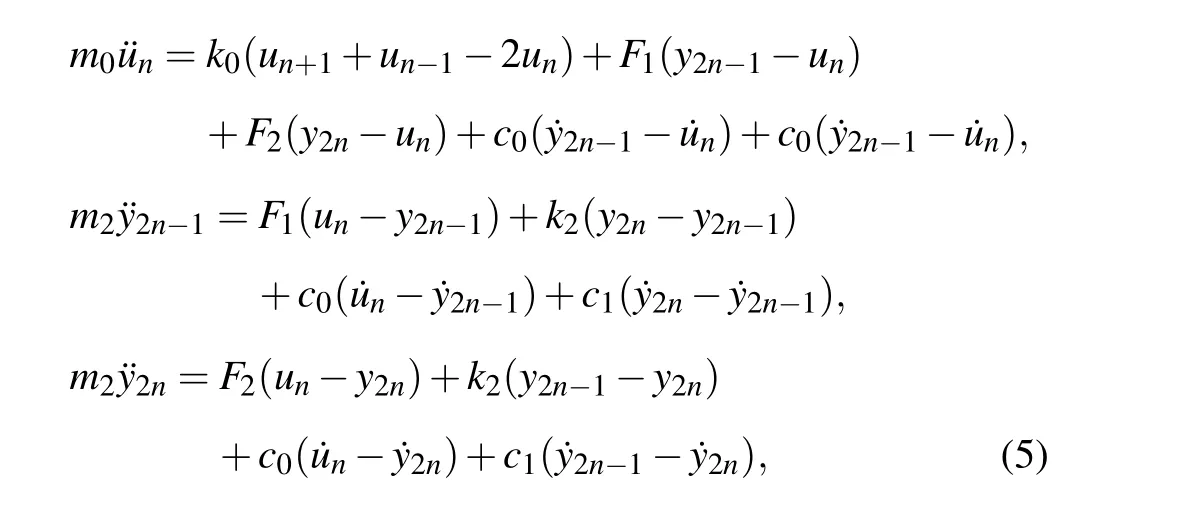
wherey2n-1andy2nare the displacements of the two resonatorsm2in thenthcell,k2is the linear stiffness of the spring connecting the two resonators, andc1is the damping coefficient of the damper between them.

We note that the above three models have the same length of 12 cells. As shown in Fig. 1, in every model, the first meta-cell is subject to an incident wave sourceu0,and the last meta-cell is free. The incident displacement is expressed asu0=A0sin(ωt) in whichA0denotes the incident amplitude andω=2π fis the angle frequency. The frequency response of the elastic metamaterials can be obtained by solving the transmission of elastic metamaterial under different excitation frequenciesf.

The parameters of elastic metamaterials with three different structures are set as follows:m0=0.1 kg,m1=0.05 kg,k0= (2π·100)2·m0N/m, andk1= (2π·20)2·0.25 N/m.The parameters for collision oscillator arekN=1×1010andd=0.0003 m. In the third model,m2=0.025 kg andk2=(2π·20)2·0.25 N/m. Other parameters are the same as collision elastic metamaterials. Unless otherwise specified asc0=1 kg/s.

2.2. Numerical methods

We adopt the numerical integration approach to solve the time-domain response of these models. For mono-frequency input,the simulation time is 50 s,and the signal segment during 40 s–50 s is taken to calculate the transmission and damping properties. The simulation time is long enough for the system to reach a steady state. The transmission is quantified byT=Aend/A0, whereAendis the average amplitude of the lastm0in the chain

wherePiandVjare the peak and valley (negative) values of the signal in 40 s–50 s, respectively. We note that collision may lead to chaotic response and this method gives an average amplitude.

2.3. Damping evaluation

Fig. 2. Schematic diagram of simple harmonic motion of single degree of freedom system.

The metamaterials under investigation form a multipledegrees-of-freedom system. The index for damping ratio should also reflect the wave transmission.Therefore,we adopt a similar expression like Eq.(10)to define the corresponding damping ratio as

2.4. Vibration and damping of a meta-cell model

Before systematically studying the properties of the metamaterials,we first investigate the general dynamics of a single meta-cell in this section.

The meta-cell is driven by a displacementu0=A0sin(ωt). The frequency responses of the meta-cell,in terms ofT=A/A0under variable excitation amplitudesA0, are shown in Fig.3,whereAis the average amplitude of the resonatorm0. The frequency response of the first linear meta-cell is of course independent ofA0. Its resonant frequencies are 20 Hz and 100 Hz. The first resonant peak is not obvious in this figure because of damping(see Fig.A1(a)in Appendix A).

For the second meta-cell(see Fig.3(b)),no collision occurs when the vibration amplitude is smaller than the clearanced, on which occasion, its response is identical with the

Furthermore, we use the damping ratioςto evaluate the energy dissipation ability in the meta-cell model,as shown in Fig. 4. For the first linear meta-cell, the ratioςdepends on frequency and is independent ofA0. The peak value is always located at the resonant frequency at 20 Hz.

For the collision meta-cell,ςdepends on both frequency andA0. WhenA0is very small,the ratioςof the cell becomes large at the two resonance frequencies,andςat the resonance 20 Hz is much higher than at the other frequency 100 Hz. ForA0＜1×10-4m,ςnear 100 Hz increases lightly while increasingA0. ForA0＞1×10-4m, asm0andm1move synchronously (see Fig. B1(b)),ςat both resonances gradually decreases.

For case 1 in the sandwich-collision meta-cell,ςat the resonance frequency 100 Hz is large for smallA0. While increasingA0,ςat both 20 Hz and 100 Hz increases gradually,and a very broad band covering 20 Hz–250 Hz for the large damping ratio is generated, which indicates that the damping effect induced by sandwich-collision is very broadband. The variation trends in case 2 are similar with that in case 1, except that the damping ratio is much larger even for small input amplitude.

Fig. 3. Frequency response of meta-cells under different excitation amplitudes. (a) Linear meta-cell; (b) meta-cell with bilateral collision; (c) case 1 in sandwich collision meta-cell;(d)case 2 in sandwich collision meta-cell.

Moreover, we calculate the average damping ratioςmand the average transmissionTmfrom 1 Hz–200 Hz to evaluate low-frequency properties. Interestingly,ςmandTmare highly correlated and vary oppositely. For the specific parameters,ςm=0.1 andTm=2.72 are used for the linear metacell model. As shown in Fig.4(f),whenA0＜10-4m,Tmof all nonlinear models are smaller than that of the linear model.However, further increasingA0whenA0＞6×10-5m (the red circle in Fig.4(f)),ςmof the second model with collision reduces to a tiny value,andTmrapidly increases and becomes larger than that of the linear model.This suggests that a proper strength of nonlinearity can reduce the vibration of the system but an excessively strong nonlinearity will jeopardize the vibration reduction in the system.

As shown in Figs.4(e)and 4(f),Tmof the third sandwichcollision model remains at the valley for both cases 1 and 2 andςmincreases to 0.36 and 0.7 in cases 1 and 2 respectively,much higher than the linear model.This means that the desired hyper damping appears owing to the damping between the two resonatorsm2in the sandwich-collision nonlinear model.Moreover, asc0=0 kg/s in case 1 andc0=1 kg/s in case 2, the damping betweenm0andm2doubles the whole hyper damping ratioςmfrom 0.36 to 0.7,alongside a simultaneous reduction in the average transmissionTmfrom 2.0 to 1.55.This also signifies that the location of the damping layer would greatly influence the system property and the hyper damping is achieved.

The aforementioned analyses based on a meta-cell model show that tactic designing the strongly nonlinear model with sandwich-collision can produce hyper damping for efficient vibration reduction even under very large amplitude.

Fig.4. Damping ratio ς (a)–(d),average ratio ςm(e)and average transmission Tm(f)of meta-cells under different excitation amplitudes. (a)Linear meta-cell;(b)collision meta-cell;(c)sandwich-collision meta-cell 1;(d)sandwich-collision meta-cell 2;(e)average ratio ςm in four meta-cells;(f)average transmission Tm in four meta-cells.

3. Vibration and damping of metamaterials

In this section, we analyze the vibration and damping in the three types of elastic metamaterials with weak damping,c0=0 or 1 kg/s andc1=1 kg/s. Cases involving stronger damping are studied in the next section. The elastic metamaterials have very different properties from the meta-cell model.They have bandgaps and dense resonances in the passbands.

3.1. Bandgaps

Firstly, the dispersion curves in linearized metamaterials are calculated by using the periodic boundary conditions determined by Bloch theorem. Here only linear case is considered. For the diatomic model shown in Figs.1(b)and 1(c),the dispersion equation writes

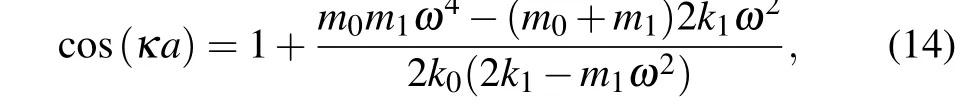
whereκ ∈[π/a] is the wave vector, andais the lattice constant.

The dispersion relationship of the model in Fig.1(d)is

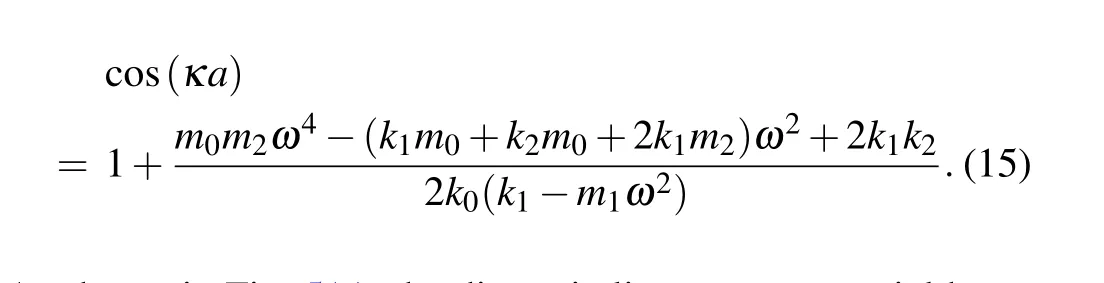
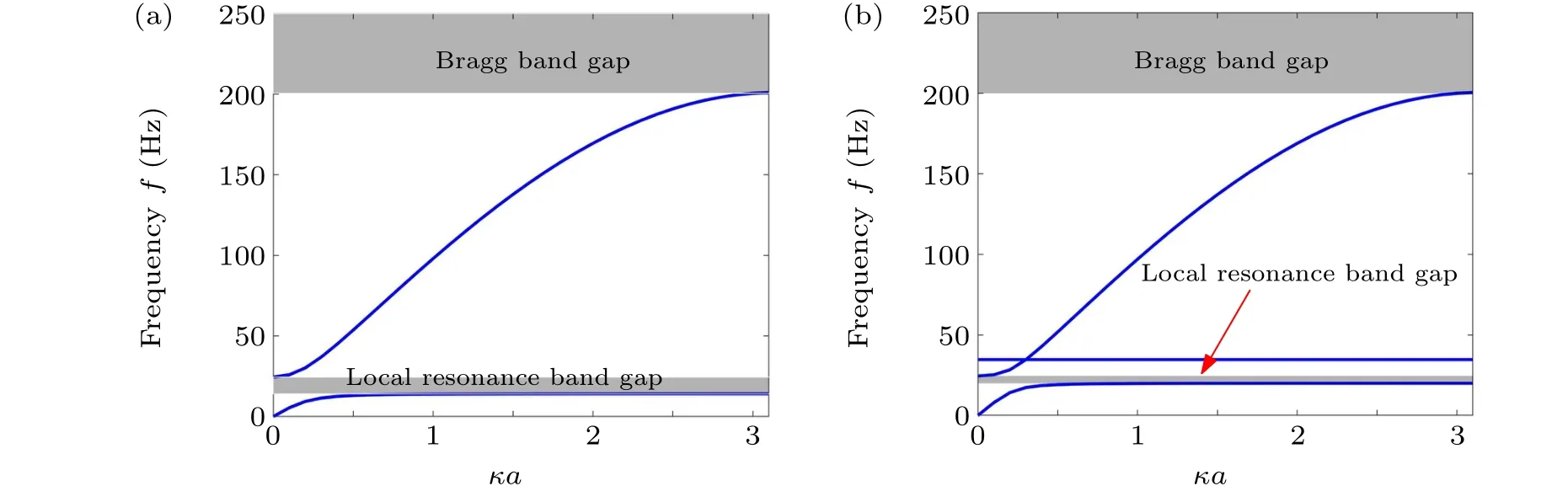
Fig. 5. Dispersion curves in linearized metamaterials. (a) Dispersion curves corresponding to Figs. 1(a) and 1(b) without collision. (b) Dispersion curves corresponding to Fig.1(c)without collision.

3.2. Vibration transmission and damping

For the linear metamaterial, as shown in Fig. 6(a), the transmission within the band gap is of course much lower than that in the pass band, and its frequency response is independent ofA0. As shown in Fig. 6(b), the peak value ofςis always located at the band gaps, because the bandgaps prohibit wave propagation,which can be regarded as the equivalent large damping effect.

For the second collision metamaterial, as shown in Fig. 7(a), its transmission in the whole passbands becomes minimal nearA0=1×10-4m,like the property observed for the meta-cell. Moreover,the damping ratio of the whole band also become larger nearA0=1×10-4m. However,the wave transmission(the damping ratio)is large(small)for both small and large amplitude, i.e., nonideal performance for vibration suppression.

Fig.6. Frequency response and ratio ς of linear metamaterials. (a)Frequency response,(b)ratio ς.

Fig.7. Frequency response and ratio ς of collision metamaterials. (a)Frequency response,(b)ratio ς.

Fig.8. Frequency response and ratio ς of sandwich-collision metamaterials under different excitation amplitudes. (a)Frequency response of case 1,(b)ratio ς of case 1,(c)frequency response of case 2,(d)ratio ς of case 2.

Fig.9. Average ratio ςm (a)and average transmission Tm (b)of meta-cells in metamaterials under different excitation amplitudes.

Properties for the sandwich-collision metamaterial are shown in Fig.8. Asc=0 in case 1,energy dissipation is only due to the relative motion between the twom2. However, as the two resonators are identical,their motions are synchronous in the ideal linear case,which means the defined damping ratio is zero. Therefore,the damping ratio in Fig.8(b)is tiny under small amplitude, on which occasion, collision does not happen. Fortunately, when increasing the incident amplitude forA0＞3×10-5m,collision betweenm0andm2takes place,the synchronous motion is then broken and the damping is active.The damping ratio increases withA0in this case within a very broadband. This evidences the collision-enhanced damping,directly responsible for the reduction in the vibration transmission in 20 Hz–200 Hz for case 2, and Figs. 8(c) and 8(d)shows similar properties with the linear metamaterial whenA0is very small.WhenA0＞1×10-4m,ςsignificantly increases withA0due to the collision enhanced damping alongside a simultaneous reduction in the vibration.

Furthermore, we evaluate the average damping ratioςmand the average transmissionTmin 1 Hz–200 Hz of these metamaterial models, as shown in Fig. 9. Their trends about the average damping ratioςmand average transmissionTmchanging withA0are similar to their meta-cell’s. And we can see that in nonlinear metamaterials the damping ratio for relatively high amplitude (with collision nonlinearity) is much higher than that for small amplitude,which exhibits the broadband hyper damping property responsible for vibration reduction. It is obvious that such hyper damping is enhanced by the collision.

4. Influences of damping on the nonlinear sandwich-collision elastic metamaterial

In this section,we clarify the effects of dampingc0andc1on the vibration transmission of nonlinear metamaterials. We numerically calculate the average transmissionTmin 20 Hz–200 Hz by changing bothA0and the damping coefficients.As there are multiple variables, the simulation with monofrequency input,u0=A0sin(ωt), is quite time-consuming to obtain the overall trends. Instead,we input the sweep-sine signal from 20 Hz–200 Hz within 200 s.The low sweeping speed used is to ensure that the responses obtained is very close to steady. The transmission spectrumT(f)is obtained with fast Fourier transform.

For the second nonlinear metamaterial model with bilateral collision (see Fig. 10(a)), the average transmissionTmis always large forc0＜4 kg/s and increasingc0can open a parameter space(c0,A0)forTm＜1(i.e.,0 dB).There is an optimal range forc0to generate a minimalTm. However,Tmalways becomes large under larger incident amplitudeA0.

For the third sandwich-collision model,we first study the influences ofA0andc0under weak damping between the two local resonatorsc1=1 kg/s (see Fig. 10(b)), and then study the influencesA0andc1for weak damping betweenm0andm2,c0=1 kg/s(see Fig.10(c)). It is interesting that this metamaterial model has much larger parameter space (c0,c1, andA0) forTm＜1 than the first model, which greatly improves the robustness in practice. Moreover,there is an optimal value ofc0(=11 kg/s here)for the minimalTmin the first case withc1=1 kg/s. Unusually,Tmbecomes large again for strong dampingc0in the first case.This trend also happens in the former nonlinear model shown in Fig.10(a). This means that one still has to optimize the damping layer betweenm0and the inner resonators in practice. Fortunately,the trends in Fig.10(c)show that the metamaterial with sandwich-collision is insensitive toc1,highlighting a robust feature.

It is well known,the phase diagram of the steady-state response of a linear damping system under single frequency excitation is a standard ring,as shown in Fig.10(i). Figure 10(h)stands for a quasi-periodic state which consists of several superimposed rings. While the phase diagrams of Figs. 10(d)–10(g)can not form one or several rings as Figs.10(h)and 10(i),which show the chaotic property.

Fig.10. Average transmission Tm of collision metamaterials and sandwich collision metamaterials with different c0 and c1. Also with the phase diagram of the 12th meta-cell marked in(a)and(b). (a)Average transmission Tm of collision metamaterials with different c0. (b)Average transmission Tm of sandwichcollision metamaterials with different c0,in which c1=1.(c)Average transmission Tm of sandwich-collision metamaterials with different c1,in which c0=1.(d)–(i)Phase diagram obtained by single frequency excitation corresponding to the points marked in(a)and(b),the frequency of excitation is 100 Hz.

In short, the nonlinear metamaterial with sandwich collision can efficiently suppress low-frequency and broadband vibration,and meanwhile features strong robustness for varying or uncertain amplitude and damping.

5. Conclusion

This paper proposes the design of a hyper-damping nonlinear elastic metamaterial for efficient,robust,low-frequency and broadband vibration reduction, along with a systematic analysis of underlying mechanism and the effects of major system parameters. To this end,we study the properties of the nonlinear elastic metamaterial consisting of sandwich damping layers and collision resonators. The vibration transmission and damping ratio of three kinds of metamaterials, and the dynamics of a unit cell are numerically studied. We find that the hyper damping can be induced and enhanced by the collision in meta-cells, consisting of resonators coupled as a sandwich structure. The sandwich collision elastic metamaterial possesses a large parameter space(amplitude,damping,frequency), whose effective tuning can warrant efficient lowfrequency and broadband vibration reduction through wave manipulation.

In conclusion,this paper,through tactic structural design,reveals new properties and possibilities that can be offered by nonlinear elastic metamaterials. Hopefully, it can offer new impetus to the grooming area of nonlinear metamaterial design and offers a novel and robust method for achieving efficient low-frequency and broadband vibration suppression.

Acknowledgments

Project supported by the National Natural Science Foundation of China (Grant Nos. 11872371, 11991032, and 12002371) and the Science and Technology Innovation Program of Hunan Province,China(Grant No.2020RC4022).

Appendix A:Frequency responses of meta-cells

As shown in Fig. A1(a), by comparing frequency responses of linear meta-cell with damping(c0=1)and without damping (c0=0), we can see that the low-frequency peak is not obvious when there is relatively large damping. As shown in Figs. A1(b)–A1(d), for nonlinear meta-cell, frequency responses change with excitation amplitudes,and there is an optimal excitation amplitude range for vibration suppression.

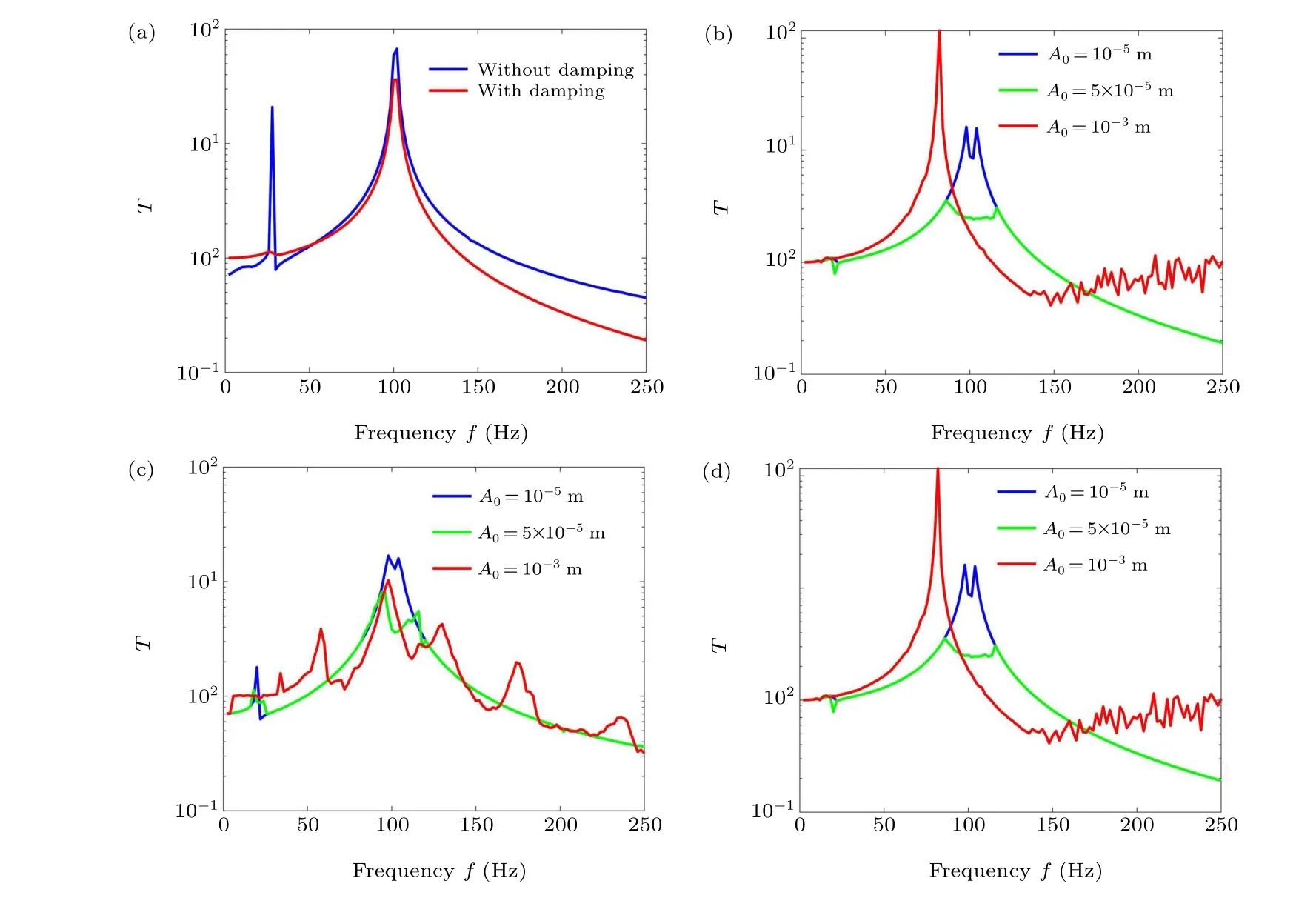
Fig. A1. Frequency response of linear meta-cell with and without damping, and nonlinear meta-cells under different excitation amplitudes. (a)Linear meta-cell;(b)collision meta-cell;(c)sandwich collision meta-cell 1;(d)sandwich collision meta-cell 2.

Appendix B: Time-domain di

agrams of the meta-cells

As shown in Figs. B1(a) and B1(c), when the amplitude of excitation is small,m0andm1orm2move in opposite phase for collision and sandwich collision meta-cell.With amplitude of excitation increasing,m0andm1move synchronously for collision meta-cell, as shown in Fig. B1(b). While for sandwich collision meta-cell 1,m0andm2move in the same phase but not synchronized,the displacement of the twom2in their non-collision direction is greater than that of them0.

Fig. B1. Time domain responses of meta-cells, the frequency of excitation is 100 Hz. (a) Collision meta-cell when A0 =10-5 m. (b) Collision meta-cell when A0=10-3 m. (c)Sandwich collision matecell 1 when A0=10-5 m. (d)Sandwich collision matecell 1 when A0=10-3 m.

Appendix C:Frequency responses of metamaterial models

As shown in Fig.C1,we can conclude that the frequency response of linear metamaterial model is independent of excitation amplitude and there is also an optimal excitation amplitude range for vibration suppression.

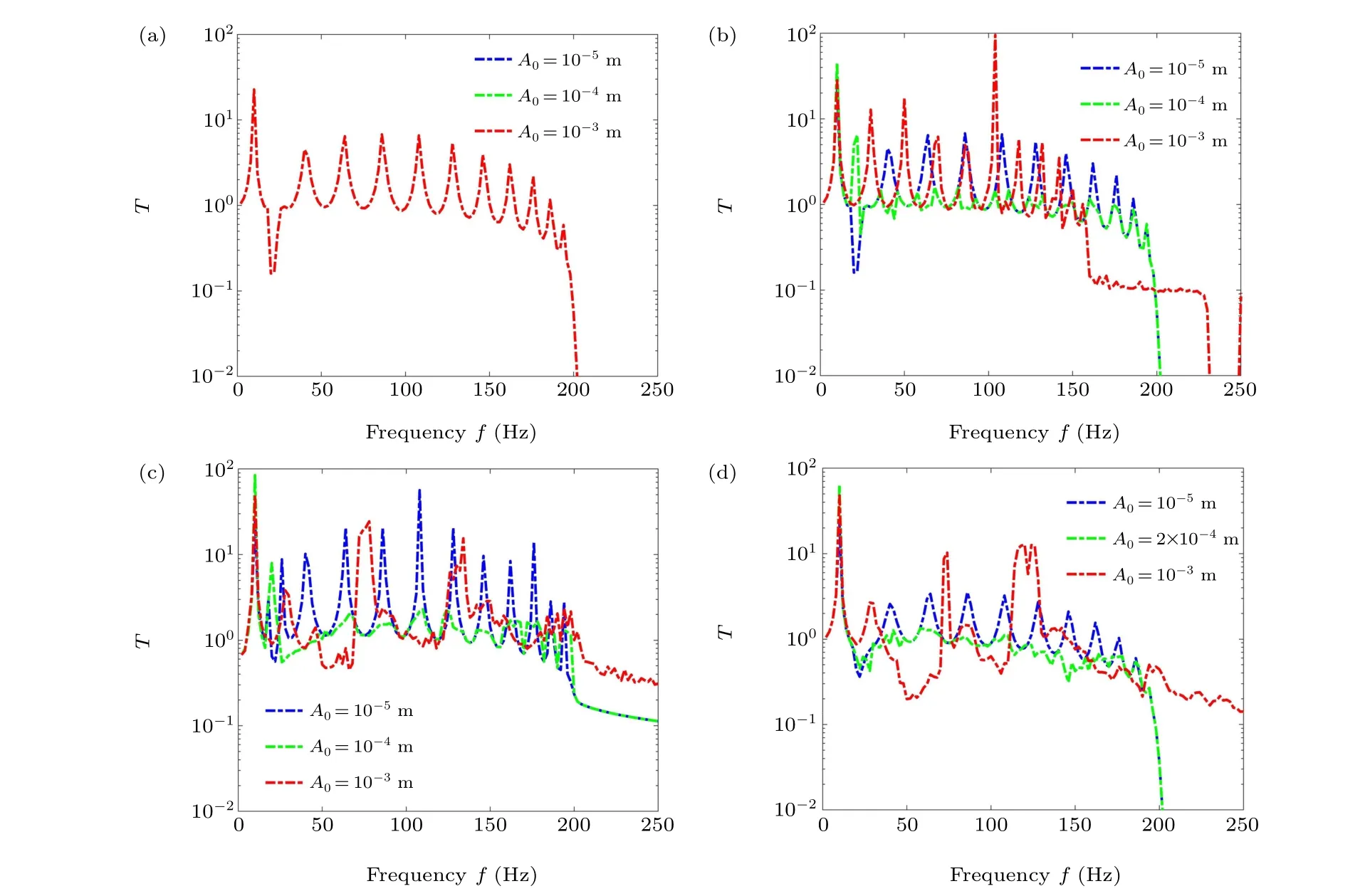
Fig.C1.Frequency response of metamaterial under different excitation amplitudes.(a)Linea metamaterial.(b)Collision metamaterial.(c)Sandwich collision metamaterial 1. (d)Sandwich collision metamaterial 2.