考虑误分类约束的电力系统暂态稳定评估

周惠怡，刘颂凯，张 磊，张雅婷，毛 丹，晏光辉

（1.三峡大学电气与新能源学院，宜昌 443002；2.佛山电力设计院有限公司，佛山 528000）

随着现代电力系统的快速发展，系统规模逐渐扩大，新能源渗透率不断升高，电力电子元件动态特性愈加复杂，这对电力系统安全稳定运行提出巨大挑战[1]。系统运行人员若无法快速、准确地判断电力系统的实时运行状态，并采取相应的控制措施，则系统可能会出现连锁故障甚至大停电事故[2]。为了及时掌握电力系统运行态势，降低因暂态失稳造成的经济损失和社会影响，制定实时可靠的暂态稳定评估方案是保障电力系统安全稳定运行的有效途径[3-4]。

目前，电力系统暂态稳定评估研究方法主要包括机理分析法及机器学习法。传统的机理分析法，即时域仿真法[5-6]和能量函数法[7-8]局限于数据处理速度不足，难以达到现代电力系统暂态稳定评估的实时性需求。

随着同步相量测量单元PMU（phasor measure⁃ment unit）和广域测量系统 WAMS（wide area mea⁃surement system）在电力系统中的发展与应用，电力系统运行数据的收集和积累变得更加方便快捷。大量的量测数据为基于机器学习的电力系统暂态稳定评估研究奠定了坚实的基础。文献[9]通过集成学习和多目标规划来泛化单个极限学习机ELM（extreme learning machine）训练的随机性，提高了暂态稳定评估结果的可靠性。文献[10]基于改进卷积神经网络 ICNN（improved convolutional neural net⁃work）构建电力系统暂态稳定评估模型，提高了模型的泛化能力。文献[11]基于支持向量机SVM（support vector machine）和决策函数实现电力系统暂态稳定评估，解决了机器学习方法保守性不足的问题。文献[12]基于生成对抗网络GAN（generative adversarial network）构建暂态稳定评估方案处理电力系统数据缺失问题。

上述基于机器学习的电力系统暂态稳定评估研究一般侧重于提高评估准确率Acc（accuracy），较少考虑误分类问题，即对失稳样本的漏判和对稳定样本的误判，而该误分类事件可能产生不可预测的严重后果。其中，相较于暂态稳定评估误判事件，漏判事件可能导致更严重的后果，对电力系统运行、人民生活及社会经济的影响更具灾难性。因此，对机器学习模型的漏判率FPR（false pasitive rate）进行限制，制定考虑误分类约束的电力系统暂态稳定评估研究是十分必要的[13-14]。

针对误分类问题，本文从数据和算法两方面来分析误分类事件产生的原因。在数据方面，由于电力系统中失稳情况很少发生，导致用于暂态稳定研究的失稳样本及稳定样本间存在严重的类别分布失衡问题，使训练好的模型偏向于稳定样本，从而造成误分类事件；在算法方面，一般机器学习方法并不具备对漏判和误判情况区别考虑的能力，因而不能有效的限制模型的FPR。

基于上述分析，本文提出了一种考虑误分类约束的电力系统暂态稳定评估方法。首先，通过自适应综合过采样ADASYN（adaptive synthetic sam⁃pling）算法[15]对输入数据进行过采样，以改善失稳样本和稳定样本间的类别不平衡问题；然后，利用群体最大信息系数PMIC（population maximal infor⁃mation coefficient）[16]探索电力系统运行变量与暂态稳定指标之间的相关性，筛选相关性较强的关键特征，以降低输入数据的维度，提高评估模型的计算速率，并降低模型过拟合风险；最后，基于伞式奈曼-皮尔逊NP（Neyman-Pearson）分类器[17]构建电力系统暂态稳定评估模型，该模型集成多类融入NP准则的分类器，具有优先限制FPR的特性，可灵活处理电力系统的误分类问题。

1 电力系统暂态稳定样本集建立

1.1 基于ADASYN的电力系统样本生成

由于现代电力系统的稳定性不断提高，系统在大多数情况下保持稳定运行状态，极少出现暂态失稳情况[18]。因此，用于电力系统暂态稳定评估研究中稳定样本数量远多于不稳定样本，导致严重的类别不平衡问题，造成暂态稳定评估模型的评估性能和泛化能力下降，进而出现误分类情况。为此，本文引入ADASYN对少数类失稳样本进行过采样，以改善样本分布失衡问题，提高模型评估性能。其基本原理如下。

给定含有p个少数类失稳样本和q个多数类稳定样本的数据集。

1.2 基于PMIC的电力系统关键特征选择

虽然PMU可采集丰富的电力系统运行特征数据，但若将其全部作为评估模型的输入，不仅不能提高机器学习模型的性能，还增大了模型的学习难度，甚至导致维数灾害；此外，大量无关特征会影响模型的泛化性能，导致模型出现过拟合风险。为了解决上述问题，本文引入基于PMIC的特征选择方法对电力系统运行特征进行数据降维。该方法首先利用PMIC分析电力系统运行特征与暂态稳定指标之间的相关性，并获取相应的相关性系数，即PMIC值；然后，筛选出与暂态稳定指标相关性较强的关键特征作为伞式NP分类器的输入数据，剔除其余弱相关特征和无关特征，以达到降低伞式NP分类器输入数据维度，提高其计算效率的目的。其基本原理如下。

2 基于伞式NP分类器的暂态评估模型

伞式NP分类器的基本思想是利用NP准则对传统分类器，包括随机森林RF（random forest）、自适应增强ADA（AdaBoost）算法和SVM进行优化，获取相应的NP分类器为NP-RF、NP-ADA和NP-SVM，并通过设置合理的FPR阈值来限制各NP分类器的FPR。传统分类器与NP分类器对比如图1所示，由图1可知，与传统分类器相比，NP分类器具有更低的FPR；基于伞式NP分类器构建电力系统暂态稳定评估模型，可显著提高模型对失稳样本的判别率，使系统运行人员可以准确的把握系统运行状态，及时采取相应的控制措施来避免大停电事故。

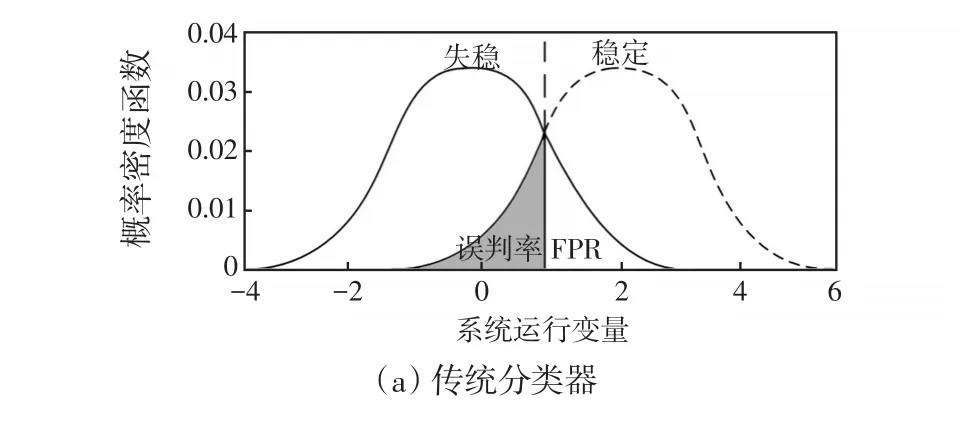
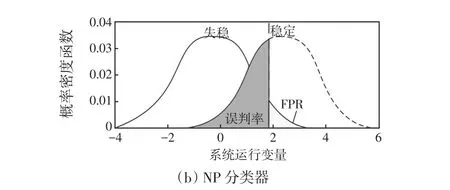
图1 传统分类器与NP分类器对比Fig.1 Comparison between traditional and NP classifiers

2.1 NP准则

NP准则的基本思路是根据两种不同误分类（漏判和误判）对分类结果的重要性，通过设置一类误分类的阈值来优先限制此类误分类率，在此基础上，最小化另一类误分类概率，以降低分类结果所产生的不利影响。本文将NP准则引入电力系统暂态稳定评估领域，由于对稳定样本的误判和对失稳样本的漏判所产生的代价不同，以优先限制FPR为基础，同时尽量降低误判率，实现对电力系统暂态稳定评估误分类的灵活约束。

2.2 伞式NP分类器训练流程

图2为伞式NP分类器训练流程，由图2可知，采用五折交叉验证法将电力系统暂态稳定样本集划分为训练集和测试集，对伞式NP分类器进行训练，建立电力系统关键运行特征与暂态稳定指标之间的映射关系。具体训练流程如下。

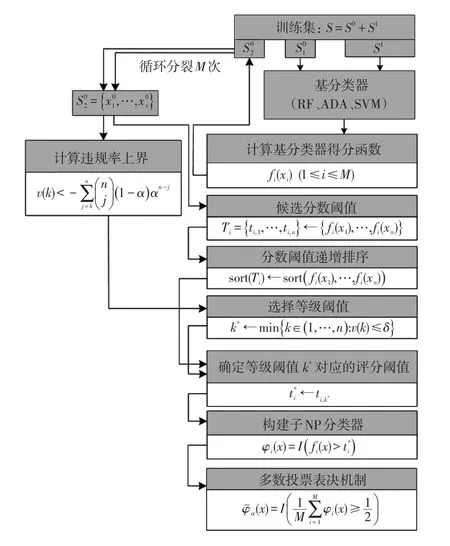
图2 伞式NP分类器训练流程Fig.2 Training process of umbrella NP classifier

2.3 模型评价指标

电力系统暂态稳定是指电力系统受到大扰动后，各发电机保持同步运行并恢复至稳态运行情况的能力[19]。因此，可利用扰动后各发电机转角差来表征系统的暂态稳定性[20]，即

式中，Δδmax为扰动后任意2台功角差的最大值。若σ>0，则系统稳定，暂态稳定标签为1；若σ<0，则系统失稳，暂态稳定标签为0。

针对电力系统暂态稳定评估问题，定义混淆矩阵表示模型对测试样本的分类性能如表1所示。其中，TP、TN分别为预测正确的稳定样本和失稳样本数量；FN为预测错误的稳定样本数量；FP为预测错误的失稳样本数量。

表1 混淆矩阵Tab.1 Confusion matrix

Acc是评价模型分类性能的常用指标，但不能反映对不同类别样本的重视程度[21]。由于对失稳样本的误判会造成更严重的后果，应更加重视模型识别失稳样本的能力。因此，除Acc外，本文还引入FPR和平衡分数F1值来更全面地评价暂态稳定评估模型的性能。其中Acc、FPR和F1的值可表示为

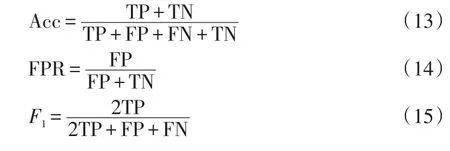
3 暂态稳定评估流程

针对电力系统暂态稳定评估误分类问题，本文提出了如图3所示的考虑误分类约束的电力系统暂态稳定评估方法，该方法主要包括离线、更新和应用3个阶段。

图3 暂态稳定评估流程Fig.3 Flow chart of transient stability assessment

3.1 离线阶段

（1）通过电力系统仿真软件PSS/E进行暂态仿真，获取包含电力系统运行特征和暂态稳定指标的原始数据库。

（2）基于ADASYN对仿真样本进行数据过采样，自适应地合成少数类失稳样本，改善稳定样本与失稳样本的分布失衡问题。

（3）利用PMIC挖掘电力系统运行变量与暂态稳定指标间的相关性，筛选出与电力系统暂态稳定指标高度相关的关键特征。

（4）基于五折交叉验证法将样本集分为训练集和测试集。使用训练集训练伞式NP分类器，建立电力系统输入特征与暂态稳定指标的映射关系。基于伞式NP分类器在测试集上的性能测试结果对其进行参数调整，以获得性能最佳的模型。

3.2 更新阶段

对于现代电力系统而言，系统工况会因计划维护、经济调度和最优潮流等可能的运行需求而发生变化，离线数据库不可能涵盖所有的运行工况，实时可靠的电力系统暂态稳定评估难以得到保障。因此，为了适应电力系统运行工况的变化，提高评估模型的泛化能力，本文设计了暂态稳定评估模型的更新阶段，其具体过程如图4所示。

图4 模型更新机制Fig.4 Model update mechanism

通常，可从电力公司获取电力系统潜在的运行工况列表；然后，根据工况列表生成相应的样本集来训练一系列的候选暂态稳定评估模型，以降低训练好的模型在应用时遇到未知工况的概率。

当电力系统出现新的运行工况时，应立即判断其是否包含在离线数据中。若已包含在离线数据中，则选择对应训练好的模型进行暂态稳定评估；否则，将对暂态稳定评估模型进行重构，训练新的暂态稳定评估模型。随着模型更新过程的执行，遭遇未知工况的概率逐渐降低，模型的泛化能力不断提升。

3.3 应用阶段

当从WAMS服务器接收到所选关键特征的实时PMU量测数据时，训练好的暂态稳定评估模型将立即给出评估结果。如果电力系统当前的运行状态被评估为稳定，系统将继续被监测；否则，将向系统运行人员发出报警信号。

4 算例分析

为验证本文所提暂态稳定评估方法的可行性，采用新英格兰10机39节点系统和仿真软件PSS/E提供的1 648节点系统进行算例分析。编程语言为R，计算机配置为Intel（R）Core（TM）i5-9300H CPU/16.0 GB RAM。使用电力系统仿真软件PSS/E进行电力系统暂态稳定样本生成。

4.1 数据集生成

新英格兰10机39节点系统包括39条母线，10台发电机和46条传输线路；PSS/E提供的1 648节点系统包括1 648条母线，313台发电机和2 294条传输线路；考虑80%、85%、∙∙∙、120%共计9种负荷水平，设置三相短路故障，故障位置位于传输线路的0、50%、90%处，故障持续时间为0.1 s、0.15 s、0.2 s，仿真时间为6 s。对于新英格兰10机39节点系统，总共生成4 522个样本，其中稳定样本3 768个，失稳样本754个；对于1 648节点系统，总共生成11 492个样本，其中稳定样本9 577个，失稳样本1 915个。首先，通过ADASYN对上述样本进行过采样，使失稳样本与稳定样本数量相等，对于新英格兰10机39节点系统，共生成7 536个样本；对于1 648节点系统，共生成19 154个样本。然后，利用PMIC进行特征选择，对于新英格兰10机39节点系统，选取30个关键特征作为伞式NP分类器的输入数据；对于1 648节点系统，选取500个关键特征作为伞式NP分类器的输入数据。最后，采用五折交叉验证法，随机选取上述样本的80%作为训练集，其余20%作为测试集对伞式NP分类器进行性能测试。

4.2 特征选择的意义

为验证本文所提基于PMIC的特征选择方法的有效性，选取不同数量的输入特征对NP-RF模型进行性能测试。其中，模型在新英格兰10机39节点系统中的测试结果如图5所示；在1 648节点系统中的测试结果如图6所示。在图5中，当特征数量为30时，模型Acc为96.14%，训练时间为23.38 s，之后再增加输入特征，模型Acc无显著变化，但模型训练时间明显增加。在图6中，当特征数量为500时，模型Acc为95.12%，训练时间为140.26 s，之后再增加输入特征对模型Acc也无明显提升。由此可知，在模型输入与暂态稳定分析无关或相关性较弱的特征时，对其评估性能的提升十分有限，但模型的训练耗时会大幅增加。因此，为了减少计算资源的浪费，使用本文所提基于PMIC的特征选择方法对电力系统运行特征进行数据降维很有意义。

图5 新英格兰10机39节点系统中模型性能随特征数量变化关系Fig.5 Relationship between model performance and number of features in New England 10-machine 39-bus system

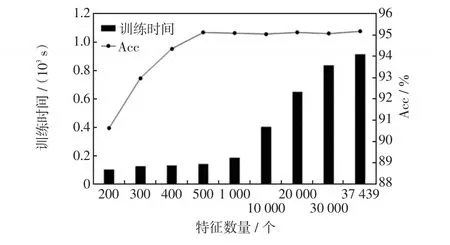
图6 1 648节点系统中模型性能随特征数量变化关系Fig.6 Relationship between model performance and number of features in 1 648-bus system

4.3 模型性能测试

为测试伞式NP分类器（NP-RF、NP-ADA、NPSVM）的评估性能。设置FPR阈值α及违规率δ默认值分别为0.02和0.05，测试结果如表2所示。

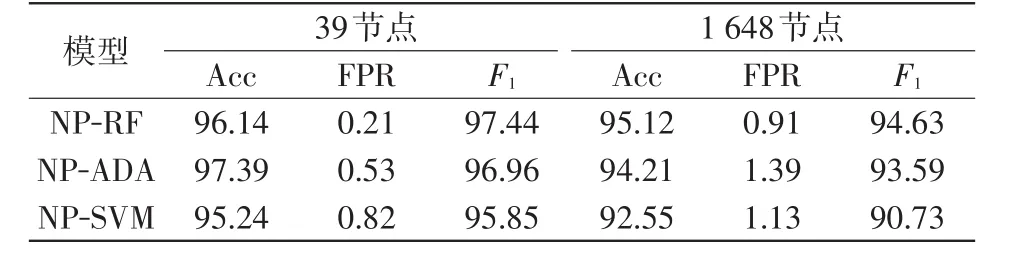
表2 伞式NP分类器性能测试结果Tab.2 Performance test results of umbrella NP classifiers%

由表2可以看出，在新英格兰10机39节点系统和1 648节点系统中，NP-RF、NP-ADA和NP-SVM Acc均大于90%，FPR均小于2%，F1值均大于90%；对于新英格兰10机39节点系统，NP-ADA的Acc最高，为97.36%，而NP-RF的FPR最低，为0.21%；对于1 648节点系统，NP-RF兼具最高的Acc为95.12%和最低的FPR为0.91%。系统运行人员可根据实际的需求选择合适的NP分类器对电力系统进行暂态稳定评估。

为验证伞式NP分类器在限制FPR方面的有效性，将其与传统分类器RF、ADA、SVM进行对比，RF、ADA、SVM均使用默认参数，测试结果如图7和图8所示。

图7 在新英格兰10机39节点系统上的FPR测试结果Fig.7 Test results of FPR on New England 10-machine 39-bus system

图8 在1 648节点系统上的FPR测试结果Fig.8 Test results of FPR on 1 648-bus system

由图7和图8可知，对于新英格兰10机39节点系统，NP-RF、NP-ADA、NP-SVM的FPR相比于RF、ADA、SVM，分别降低了0.94%、1%、0.42%；对于1 648节点系统，NP-RF、NP-ADA、NP-SVM的FPR相比于RF、ADA、SVM，分别降低了0.64%、1.07%、0.54%。总体而言，相比于传统分类器，伞式NP分类器具有更低的FPR，在限制暂态稳定评估漏判事件方面更具有优势。

4.4 FPR阈值设置

为测试FPR阈值α对伞式NP分类器Acc和FPR的影响，本文将FPR阈值α分别设置为0.01、0.03、0.05、0.07、0.09，并进行暂态稳定评估测试，测试结果如图9和图10所示。

图9 FPR阈值在新英格兰10机39节点系统测试结果Fig.9 Test results of FPR threshold on New England 10-machine 39-bus system

图10 FPR阈值在1648节点系统测试结果Fig.10 Test results of FPR threshold on 1648-bus system

由图9和图10可知，通过设置不同FPR阈值可将伞式NP分类器的FPR限制在不同范围内，且伞式NP分类器的Acc也随FPR阈值变化而变化。当阈值α为0.05时，伞式NP分类器Acc达到最高，但此时分类器的FPR也有所提高。在实际应用中，系统运行人员可根据需求调节FPR阈值参数，实现Acc和FPR的灵活约束。

4.5 鲁棒性测试

为进一步分析伞式NP分类器对电力系统拓扑变化的鲁棒性，通过改变系统网络拓扑结构来增加几种新的运行场景。设定新英格兰10机39节点系统：7号发电机退出运行为场景1；线路6-11和线路15-16退出运行为场景2；5号发电机和线路17-27退出运行为场景3。设定1 648节点系统：线路6-10退出运行为场景4；51号发电机和线路89-92退出运行为场景5；137号发电机和线路55-76退出运行为场景6。设置FPR阈值α及违规率δ为默认值，测试结果如表3和表4所示。

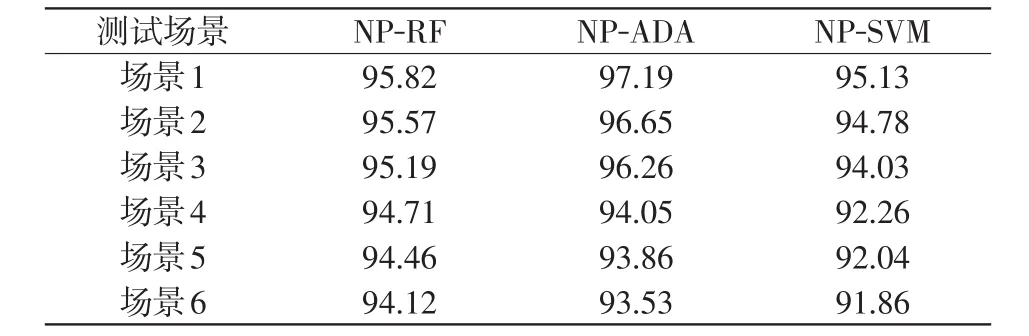
表3 新场景下Acc测试结果Tab.3 Test results of Acc in new scenarios%

表4 新场景下FPR测试结果Tab.4 Test results of FPR in new scenarios %

由表3和表4可知，虽然电力系统的网络拓扑结构发生变化，伞式NP分类器的Acc仍然维持在90%以上，且FPR均低于2%。综上所述，伞式NP分类器对电力系统网络拓扑结构变化具有较强的鲁棒性。

5 结论

本文提出一种考虑误分类约束的电力系统暂态稳定评估方法，在新英格兰10机39节点系统及1 648节点系统上进行了算例分析，得到如下结论：

（1）针对电力系统样本分布不平衡问题，将ADASYN算法用于数据过采样，改善稳定样本与失稳样本的分布，提高伞式NP分类器评估性能；

（2）针对电力系统运行特征高维的特性，将PMIC算法用于数据降维，筛选出与暂态稳定指标高度相关的关键特征作为伞式NP分类器的输入，有效地提高了模型的计算效率；

（3）针对电力系统暂态稳定评估误分类问题，采用基于NP准则的伞式NP分类器构建暂态稳定评估模型，可有效限制模型的FPR，显著提高模型对失稳样本的判别率，确保电力系统安全稳定运行；

（4）针对实际电力系统运行工况复杂多变的特性，设计了模型更新机制，提高暂态稳定评估模型的泛化能力。