细磨多粒级动力学试验与模拟

李 沛，邓中诚，池慧强，赵善忠，曹 钊

(内蒙古科技大学 a. 矿业与煤炭学院；b. 内蒙古自治区矿业工程重点实验室，内蒙古 包头 014010)

磨矿动力学主要研究被磨物料粒度分布随作业时间、能量输入的演化过程及其随工况变动的规律，研究方式为测定粉碎速度函数和粉碎分布函数，目标是在总量平衡模型的框架下预测磨矿产品的细度、产能与能耗，以此优化设备与工艺[1-2]。

粉碎速度(breakage rate)Si是指单位时间内第i个粒级物料碎裂后并转移至更细级别的质量分数，其集合为粉碎速度函数S，可通过多组单粒级磨矿试验和一阶动力学回归分析获得[3]。粉碎分布(breakage distribution)bij是指j粒级物料被粉碎的部分转移至i粒级的质量分数 (以j粒级被粉碎部分为基)，累计形式为Bij，有Bij-Bi,j+1=bij，其集合为粉碎分布函数B，可通过单粒级短时间磨矿并用BII或零阶产出率法反算[4]。由此可见，单粒级磨矿试验中物料的粒级纯度决定着动力学函数测定的准确性。

然而，对于细磨，难以制备足够多的高质量单粒级物料。例如，在某优化铁矿细磨研究中，为保证介质群的正常运动，磨机筒体必须足够大，假如选用筒体尺寸为φ360 mm×300 mm，则单次试验需5 kg左右的物料，而且筛分制备粒径为100 μm以下高粒级纯度的物料极为困难。例如，制备粒径为53～75 μm的单粒级物料时，首先分批次干筛(每次100 g物料分批给入振筛机筛分15 min)，之后用湿式手筛检查，其中只有50%的物料合格。由此可见，在实验室中制备千克级微细物料工作量极大，勉强能在探索性试验中应用，难以支撑系统性的研究工作。对此，应开发多粒级的磨矿动力学试验与动力学函数反算方法。

本文中以陶瓷球细磨铁矿试验研究为例，首先制备百克级的小质量单粒级物料，用BII法得到粉碎分布函数；用多粒级给矿做动力学试验，获得不同磨矿时间或能量输入水平的粒度分布；以拟合所得粒度分布尽可能接近观测值为目标，通过非线性规划找到合适的粉碎速度函数；最后，配合磨矿净功率计算，利用总量平衡模型(population balance model)模拟磨矿效果随作业条件的变动规律，以期为磨矿方案评定、工艺设计和设备选型提供量化依据。

1 磨矿动力学理论

1.1 粉碎函数与总量平衡模型

一般的，单粒级磨矿速度可用一阶动力学方程定义

lnwi=ln 100-Sit，

(1)

式中：wi为i粒级物料的质量分数，%；t为磨矿时间，min；Si为i粒级物料的粉碎速度，1/min，可将单粒级磨矿试验若干时间点的wi对数化后对t做线性回归而得。

(2)

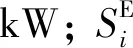
如果以比能量代替时间，则批次磨矿的总量平衡模型为

(3)

式中：E为磨矿过程中输入的比能量，(kW·h)/t，一般认为是介质支取的部分(对应的功率即Pbal)而不计物料支取的部分；wi(E)为比能量E的函数。该模型有解析解[3]

Mp=(TJT-1)Mf，

(4)

式中：Mf为给矿矩阵，Mf=[wi(0)|i=1,2,3,…,n]n×1；Mp为产品矩阵，Mp=[wi(E)|i=1,2,3,…,n]n×1；J为对角矩阵，T为下三角矩阵，其元素分别为Jij与Tij，即

(5)

(6)

当探明粉碎速度函数和粉碎分布函数，便可用总量平衡模型估计物料的粒度分布随比能量的变动情况。磨机平稳运行时功率基本恒定，则在一定工况条件下，输入的比能量正比于磨矿时间。为便于理解，本文中采用后者表述。

1.2 动力学函数拟合

细磨范围内粉碎速度函数一般是单调函数，即曲线无拐点，拟合公式为[8]

(7)

粉碎分布函数拟合的形式为

(8)

式中：di为i粒级的上限，而dj+1为j粒级的下限，μm，这样设置可在数学上保证B21恒为1；β0、β1、β2为拟合参数，无量纲，在部分早期文献中dj+1被dj取代，拟合参数会相应变化。

若粉碎分布函数是可规范化的(normalized)，即相对粒度di/dj+1而非实际粒度决定分布，则上式β0为常数；若不可规范化，即实际粒度也影响分布，β0随粒度变化，记作β0j，计算公式为

(9)

式中：β00、β01为参数，无量纲，且β0j最大为1。

1.3 拟合参数反算

基于多粒级磨矿动力学试验反算拟合参数的原理是：预估拟合参数初值，按一定方法调整数值即可获得不同的磨矿动力学函数，进而不断更新模拟所得粒度分布，直至与实测值接近。这可抽象为非线性规划求解[7]

(10)

式中：min为最小值函数；i为粒级序号，由大到小排序，n为粒级总数；k为观测点序号，m为试验点总数;Pi,kt为试验所得第k个试验点里磨矿产品中i粒级上限对应的负累计，%；Pi,kc为计算所得第k个试验点里磨矿产品中i粒级上限对应的负累计，%。

第k次试验的拟合精度可用以下标准相对残差σk衡量，计算公式为

(11)

这类规划求解问题可通过内置在Excel中的GRG算法(广义简约梯度法)解决。本文中采用基于Excel开发的Moly Cop Tools计算，该工具操作简便，数据结构清晰，二次开发方便。

实践表明，粒级较少(n≤6)且观测点数较少时(k≤4)，得到的拟合参数组合并不准确，须减少参数数量。考虑到粉碎分布函数主要由矿石性质决定，一定程度上受介质种类影响[9]，而几乎不受磨机尺寸和其他工况的影响[5,10]，因此可使用小滚筒做单粒级磨矿试验(50～100 g样品)以测定Bij。如此，式(10)中变量仅剩α0、α1。

2 磨矿动力学试验

2.1 千克级多粒级

在试验平台上对铁矿细磨给矿做多粒级的磨矿动力学试验，过程中记录磨机筒体扭矩以计算机械功率，在设定时间点停止磨矿从矿浆中取样，通过湿式筛分获得粒度分布。筛分烘干称重后将样品返回筒体，并相应补加水。磨矿动力学试验平台如图1所示。由图1可见，磨矿动力学试验平台由电机、转速扭矩仪、磨机筒体、控制面板、支架等组成。磨机选用尺寸为φ360 mm×300 mm的筒体，内衬光滑，保证介质群泻落式运动。

需要说明的是，对球形介质，筒体用圆筒或锥形均可，若考查非球形介质如钢段，应避免使用小尺寸锥形筒体，因其严重限制了介质群的运动。如使用尺寸为φ25 mm×35 mm钢段在实验室XQM240×90锥形球磨机运行，在一定条件下，介质间相互作用，会出现介质群“卡”住、磨机空转的现象。

被磨物为磁铁矿，全铁质量分数为55%～60%，密度为4.55 g/cm3，全部过孔径为212 μm的筛子，80%过筛粒度P80为66 μm。磨矿介质为陶瓷球，密度为3.75 g/cm3，按质量比7∶8∶5设置φ25 mm、φ20 mm、φ15 mm球形成平衡级配。磨机转速为52 r/min，转速率为74%，介质填充率为22%，总填充率为30%，矿浆固体质量分数为65%，则矿量为6.92 kg，介质量为20.6 kg。该工况下磨矿作业功率为100 W，空载功率为40 W，则磨矿净功率为60 W，其中由介质支取的功率Pbal为44 W。试验中，取样时间点分别为1、2 min，从筒体中取公斤级矿浆，搅拌缩分后取150 g左右矿浆湿式手筛，筛分尺寸分别为20、38、53、75、106、150 μm。

2.2 百克级单粒级

多粒级磨矿试验的取样点过少，数据不足以准确估计α、β这2个系列参数，考虑用百克级的物料做单粒级磨矿试验，以获取分布函数Bij，如此非线性规划中变量只留下α系列。

先用干式机过筛，再用湿式手筛，得到若干单粒级样品，每个50 g左右，分别在尺寸为φ60 mm×80 mm小筒中用φ15 mm球(介质填充率为30%)进行短时间磨矿后筛析，共2次，在粒级质量分数相对偏差小于10%的情况下取平均值。Bi通过BII法求得，若精细筛分，粒级纯度和筛分效率均可视为100%，计算可简化为

(12)

式中：Pi是磨矿产品对应i粒级上限的负累计，%；w1是产品中初始单粒级的质量分数，%。

该方法假设在短时间内新生细粒级物料为初始单粒级物料单次粉碎而得。根据经验，单粒级粉碎量应控制粒级质量分数在30%内为宜。此例中时间设为1 min，过短则部分粒级质量太小无法准确称量，过长则违反上述假设。该方法基于“零阶产率”假设，即负累计随时间线性增长。这一点在粗磨中通常成立，在细磨中需先行考查。此外，为减小工作量，可考虑仅测试部分粒级，并用类似式(10)非线性规划的方法找到参数β系列，即

(13)

式中：Bt为观测值；Bc为估计值。

2.3 磨矿净功率估算

当工况改变，特别是填充率改变后，磨矿净功率随之变动。根据经验，认为泻落式磨矿有用功率模型较合适此例，即将离散的、循环运动的介质群看作整体，由磨机筒体提供转矩维持其现有的提升位置[11]，如图2所示。

图2 泻落式磨矿物料与介质运动示意图Fig.2 Schematic diagram of movements of mineral material and media in cascading grinding

其建模过程见文献[12](推导过程有笔误但结论正确)，计算式为

(14)

式中：Pnet为净功率，kW，即用于提升介质与矿浆做周期性运动的功率，一般被指定为磨矿作业机械功率与磨机空载机械功率之差；D为磨机有效内径；L为有效长度，m；Nc为转速率，%；ρap为被提升填充物的堆密度，t/m3，包括矿浆与介质2个部分；θ0为被提升的填充物占据半圆对应的圆心角，(°)；θ1为被提升填充物质心的提升角，(°)。经验上，当使用光衬时，填充率为30%，转速率为70%左右，θ1约为30°～32°，且与填充率正相关。

本例中粒度小，矿浆流动性好，因此被提升的大部分是介质，此时ρap约等于介质的堆密度，θ0约等于介质平铺对应的圆心角，与介质填充率Jb的关系为

(15)

另外，有研究表明，相同介质制度、工作条件下，非球形介质的功率相较于球形介质的高，如钢段的功率较钢球的高5%～10%[13]，在上式中体现为形状系数λ的取值。前期试验研究表明该功率模型精度较高，在转速率为74%，矿浆固体质量分数为65%，总填充率为30%时，不同工况下对磨矿净功率的估算结果见表1。

表1 不同工况下对磨矿净功率的估算Tab.1 Estimation of net power at different milling conditions

3 细磨动力学试验结果

3.1 粉碎分布函数

粒径为150～212 μm单粒级铁矿的磨矿动力学曲线见图3，粒级质量分数对数值随磨矿时间下降速度先快后慢，偏离一阶动力学，具有非线性特征。

粒径为150～212 μm单粒级铁矿被粉碎后的负累计分布见图4，基本符合零阶产率特征，因此可用BII法估计粉碎分布B值。此外，次大粒度(150 μm)的负累计增量偏离线性为磨矿中的普遍现象，因为最大粒级的减量先快后慢。

实测细粒铁矿的粉碎分布函数如图5所示。由图5可看出，磁铁矿在细磨中的粉碎分布是非规范化的；此外，150 μm以下物料被粉碎后，其粉碎分布曲线随粒级增大而向右平移；而150～212 μm粒级的粉碎分布曲线不遵循该规律，与细粒级的曲线相交，表明该粒级的粉碎特性与细粒部分差异很大。

150 μm以下粒级的粉碎分布可用一组β参数拟合，如用106～150 μm和38～53 μm数据估计，寻求参数继而推算其余细粒级，如图6所示，其中β1为3.36，β2为20.0，β00为0.14，β01为0.67。而150 μm以上只有一个粒级，信息少，不能得到可靠的β参数。另外，106～150 μm粒级的粉碎分布拟合并不好，说明这部分的矿物学性质与细粒级差异仍然较大，从曲线走势上可看作是粒径大于150 μm部分与小于106 μm部分的过渡。考虑到全部分布函数已经得到，本例中将其直接录入程序。

3.2 粉碎速度函数

在多粒级磨矿动力学试验中，细粒铁矿的粒度分布演化观测与拟合结果如图7所示，对2 min产品拟合的标准残差σ为2.26，对4 min产品拟合的标准残差σ为1.62，效果较好。观察负累计观测与拟合的偏差，发现其在粗粒级中小而在细粒级中大，这是因为随着从细到粗粒级质量分数的累加，正负偏差相消，使负累计的偏差逐渐减小。

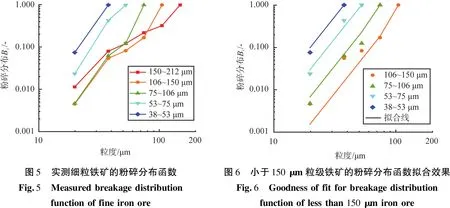
图7 铁矿细磨的粒度分布演化观测与拟合结果Fig.7 Observation and simulated results of particle size distribution evolution of iron ore fine grinding

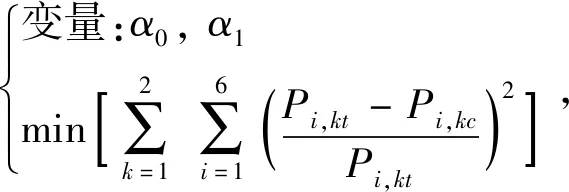
(16)

在探明细粒级铁矿粉碎分布函数的基础上，通过式(16)获得参数α0为1.80×10-3，α1为1.57，则获得细粒级铁矿粉碎的速度函数，见图8。

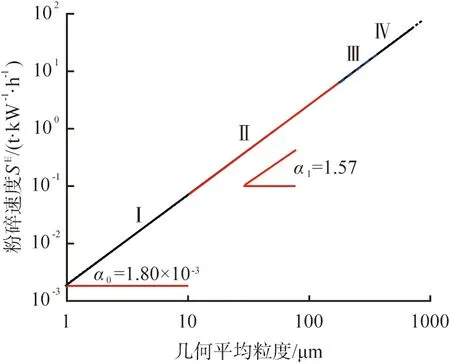
图8 铁矿细磨的粉碎速度函数Fig.8 Breakage rate function of iron ore fine grinding

在给定磨矿条件下，粉碎速度函数随粒度增大一定会有最大值，所以SE曲线不能大幅度外延。图8中，Ⅰ为超细磨阶段，粉碎特性改变极大，属低可信度区间；Ⅱ为试验区间且粒度范围较窄，属高可信度区间；Ⅲ为Ⅱ的适当外延，属中等可信度区间；Ⅳ超出试验区间过多，属低可信度区间。在细磨中小颗粒所需粉碎能很小，一般情况下即使小尺寸的轻质介质也会产生足够的冲击能量，远超颗粒碎裂的阈值，因此不出现拐点。

4 细磨中磨矿模拟与应用

4.1 相同工况下的模拟

在结果中另外安排了6 min的试验点，6 min验证试验结果如图9所示，其σ为1.93，模拟效果较好，确认了上述方法和参数的可靠性。

图9 6 min验证试验结果Fig.9 Results of 6 min grinding test for verification

通过对比图7和图9，发现2、4 min负累计观测值分布在拟合曲线两侧，符合回归的特征；而在6 min的拟合值均比实测值高。推测该现象并不是偶然，因为细磨的动力学偏离线性，粉碎速度先大后小，即2、4 min得到的粉碎速度比6 min时的大。

4.2 不同填充率下的模拟

将介质填充率和总填充率均提升至44%，进行2、4 min模拟和验证试验，以考察模型对不同填充率下的适用性。一般认为磨矿动力学参数不随填充率变化，因此只需掌握给矿粒度分布和磨矿净功率即可。据估计，该条件下的提升角θ1约为34°～40°，根据式(15)估算出磨矿净功率为77.8～89.4 W，而试验测定磨矿净功率为82.0 W。填充率为44%时，不同时间的粒度分布的观测值与模拟值如图10所示，可以看出，即使不能精准的估计磨矿净功率，变动填充率后的模拟结果也接近观测，效果较好。

4.3 磨矿模拟的应用

本文中以陶瓷球细磨铁矿为例阐述多粒级动力学试验与模拟的应用。

4.3.1 小型试验评定磨矿方案

在指定产品细度下，磨矿方案的效果包含产能与比能量2个方面，前者一般以新生合格粒级产率表达，后者以吨矿产品电耗表达。当给矿相同时，钢段(尺寸为φ25 mm×35 mm，平衡级配)与陶瓷球(直径为φ25 mm，平衡级配)细磨铁矿的方案及试验结果见表2。从表2可以看出，在介质相对矿量的比值相近时，批次磨矿中用陶瓷球代替钢段能使新生合格粒级产率增加，比能量降低。

表2 钢段和陶瓷球细磨铁矿的方案与结果Tab.2 Scheme and results of iron ore fine grinding with steel cylpebs and ceramic balls

根据现场要求，磨至小于75 μm粒级质量分数达到92%及以上为合格。各指标定义为

q75=(wf75-wp75)mH/tm，

(17)

Em=(pmtm)/mH，

(18)

式中：wf75为给矿中小于75 μm粒级的质量分数，%；wp75为产品中小于75 μm粒级的质量分数，%，此处被指定为92%；tm为达到指定细度的作业时间，min，可用总量平衡模型确定，如在Moly-Cop tools中依靠手动调节确定[9]。

相较于用等时间点比较磨矿方案效果，这种方法提供的指标更为直观。此外，配合磨矿净功率估算，可通过模拟以比较不同条件下的效果，使方案评定更为全面。尽管研究方法不同，对比钢介质，本文中陶瓷球研磨铁矿与文献[14]中的效能相近，与文献[15]中陶瓷球研磨钨矿石细粒部分的效能相似，可归纳为轻质球形介质在细磨中的优越性。

4.3.2 磨矿方案的优化

磨矿条件对动力学影响程度的排序为如下。

1)矿石性质决定磨矿动力学。

2)介质种类、球径与级配决定SE，可用统计的方法推测[5]，介质种类(密度和形状)也在一定程度上影响B[9]。

3)矿浆固体质量分数对SE影响较大，有最佳值[16]。

4)给矿的粒度分布影响较小，除非整体变得很细或很粗[17]。

5)介质填充率、总填充率、磨机尺寸、内衬设计被认为改变了磨矿净功率[5]，不影响动力学函数。

由5)可知，通过较准确的功率估算就能模拟出不同填充率下的生产指标，方便对其寻优和方案间的比较。本例中陶瓷球细磨铁矿的产率与比能量随填充率变动的模拟见图11。由图11可见，高填充率不仅能提高新生粒级产率，还降低了磨矿作业比能量。这可被解释为：磨矿所需比能量几乎不变，而随着总填充率提升，增加的被磨物料量分摊了磨机筒体转动能量，进而使磨矿作业比能量降低，实现节能效果。

图11 产率与比能量随填充率变动的模拟Fig.11 Simulation of production and specific energy as a function of charge filling

4.3.3 生产中连续磨矿的预测

批次作业与连续作业有显著区别，前者合格产品无法排出而后者可以，因而仅在试验室进行小型批次磨矿试验，不足以准确预测生产运行情况。考虑到粉碎分布函数B主要由矿石性质确定，而基于比能量的粉碎速度函数SE由矿石性质、装球制度和矿浆固体质量分数决定，二者都与磨机尺寸关系不大[5,10]，因此，可用小型试验确定SE，在总量平衡模型的框架下模拟连续开路磨矿，也可配合分级作业模型模拟闭路磨矿，近年来，相关研究成果已被尝试用于磨矿回路设计与控制[16]。其应用关键在于准确估计大磨机的运行功率和颗粒在磨机中滞留时间。前者可通过现场取值、Hogg-Fuerstenau公式估算、Morrison公式(C模型)估算或离散元仿真获得[11]；后者通过放射性示踪法标记颗粒获得，也可用流体动力学的经验公式估计[5]。磨矿回路模拟与预测思路示意图如图12所示。

图12 磨矿回路模拟与预测思路示意图Fig.12 Schematic diagram of grinding circuit simulation and prediction

4.4 细磨非线性特征对模拟的影响

需要指出的是，湿式细磨中矿石或玻璃等物料的粉碎速度往往先快后慢，即随着细粒质量增大，物料整体更难磨[18]，正如图3所示。理论上，这一特征并不符合经典总量平衡模型中“粉碎速度不随时间变化”的假设[3]，而实践表明，随着磨矿的时间延长，细粒质量的增大，在粗磨中动力学也会偏离线性甚至呈现明显的非线性特征[19]。对此，研究者们提出了若干解决方法，如引入变速系数k修正不同时间点的速度，或从数学形式上提出非线性的总量平衡模型，但相关试验工作量大，计算方法繁复，仍有待完善[18-19]。考虑到短时间磨矿偏离线性的程度不大，在精度要求一般的场景中，仍可使用本文中的方法。由此可知，预测时间点应与取样时间点相接近，以提高模拟的准确度。铁矿细磨中较粗粒级的粉碎分布规律与较细粒级的不一致，可能是由于粗、细两部分的裂隙发育程度或矿物间嵌布特性相差较大，导致两部分在断裂力学特性上的差异[20]。

5 结论

1)应用非线性规划，可以从被磨物料粒度分布演化信息中提取出磨矿动力学函数，避免制备大量单粒级微细物料的困难。

2)通过百克级的小筒体磨矿试验确定粉碎分布函数，减少参与非线性规划的拟合参数，进而从较少的试验点中也能提取相对准确的粉碎速度函数。

3)考虑到细磨动力学一定程度上偏离线性的特征，模拟时间点与取样时间点应尽量接近，以保证准确度。

4)动力学函数对填充率的变动不敏感，后者被认为仅改变了磨矿净功率，因此配合功率估算，能有效模拟磨矿效果随填充率的变动规律。

5)基于该方法进行磨矿模拟，能直观、准确地评定磨矿效果。随着研究的推进，可用小型试验预测生产中磨矿回路的作业效能，将为设计选型和作业优化提供详尽的量化依据。