生物酶改良有机质土的一维次固结双曲线特性研究

张艺馨，文畅平*，袁湘黔，汤 翔

(1. 中南林业科技大学 土木工程学院，长沙 410018;2. 现代木结构工程材制造及应用技术湖南省工程实验室，长沙 410018)

土是岩石风化的产物，土颗粒是岩石风化后的碎屑物.微生物参与土的风化作用所产生的有机质成分，一般以腐殖质为主，其主要成分是腐殖酸，具有多孔的海绵状结构，比黏土矿物具有更强的亲水性和吸附性.有机质广泛存在于天然土体中，土体按有机质含量可分为：无机土、有机质土、泥炭质土和泥炭，其中有机质土的有机质含量在5%～10%[1].有机质土具有压缩性高、塑性大、承载力低等特点.国内外学者针对有机质对土体的影响进行了大量的研究.郭印等[2]的研究表明有机质(腐殖酸)的物化特性严重影响了土的固化作用.Tremblay等[3]分析了13种有机质对土体抗剪强度的影响，该研究表明有机质的存在不利于土体的固化，影响土体的强度.

在工程中对有机质含量较高的地基或路基进行处理，传统方法有换填处理法、排水固结法、强夯法等，上述方法虽已形成相应的规范标准，但存在高费用、低效率、低环保等特点.使用改性钙基稳定剂，如石灰、水泥和粉煤灰等改良有机质土，也可达到较好的效果[4].刘子铭[5]采用复合改良剂改良有机质土，发现该复合改良剂能提高土体强度，且相对于普通硅酸盐水泥，该复合改良剂的改良效果更佳.邵俐等[6]通过掺入水泥与粉煤灰改良有机质土，有效提高了有机质土的强度.

因目前方法中CO2排放量高，对环境不友好，且工程成本高[7-8]，故迫切需要寻找一种新的改良方法.生物酶土壤固化剂(简称生物酶)作为一种新的土体改良剂，能有效地减少土体的胀缩性，使其达到工程要求，具有无毒、无腐蚀性、经济性、低碳环保等特点[9-11].文献[12-15]利用生物酶改良土体，发现改良后土体的抗剪强度相对于原状土的抗剪强度得到了显著提高.生物酶改良土体技术在国内外已得到了初步的应用[11]，但还不够成熟.

土体流变的表现形式较多.在恒荷载下，土体的变形随着时间增长的情况被称为蠕变.次固结沉降是由于蠕变造成的.1957 年，上海工业展览馆建立于土体地基上，随后其中央大厅平均沉降深度达160 cm[16]，建筑物的不均匀沉降与工后沉降变形问题均与土体次固结特性有关[17].笔者以描述生物酶改良有机质土的一维次固结特性为研究目的，开展次固结试验，对不同生物酶掺量下改良有机质土的次固结规律进行分析，建立双曲线模型参数与生物酶掺量的关系.

1 试验方法

1.1 试验材料

1.1.1 试验土体

土体取自长沙市某建筑工地，取土深度1～1.5 m，呈黄红色，表面潮湿，能被手握成团，颗粒细，孔隙小而多，其主要物理力学指标见表1.根据公路路基设计规范(JTG D30—2015)[18]判断该土体为黏土.

表1 土体基本物理力学指标

1.1.2 生物酶试剂

本试验采用的改良土体固化剂为美国NATURE PLUS 有限公司研发的Terra-Zyme(泰然酶).该酶为褐色粘稠液体制品，无毒无污染，易溶于水，具有特殊气味，其pH 值为4.3～5.3，水稳性较好.

1.1.3 土样制备

因实际土壤中有机质含量不尽相同，故需要重塑不同有机质掺量的有机质土样.国内外学者采用不同的方法配置有机质土，如储诚富等[19]采用腐殖酸钠作为外加有机质，重塑了不同有机质掺量的有机质土；徐日庆等[20]采用富里酸来配制不同有机质掺量的有机质土.而笔者使用富里酸作为外加的有机质材料，按照不同的土体干质量比，重塑有机质土壤.试验按照相关要求，根据不同的生物酶质量与土体干质量比，分别制备生物酶掺量为0.00%、0.01%、0.02%、0.03%、0.04%的有机质土试样.

1.2 试验方法

试验采用WG 型单杠杆固结仪，试样高为2 cm、横截面积为30 cm2，双面排水.试验以生物酶掺量为唯一变量，采用分级加载，初级荷载为25 kPa，最高加载至800 kPa，每级荷载加载持续时间为7 d.本试验共持续42 d，每级荷载固结稳定的标准为最后24 h 内变形量不大于0.005 mm，方可加下一级荷载，采取人工读数记录数据.

2 试验结果与分析

由于试样没有侧向变形而只存在垂直方向的固结变形，故以试样不同时刻垂直方向的变形量除以其初始高度，便可得到不同时刻垂直方向上的试样应变(等价于体积应变).各级荷载下的应变可以依据不同荷载增量下所测得的应变进行相同时刻的线性叠加而得到.因此，根据土样的次固结试验数据，分别绘制出生物酶掺量为0.00%至0.04%时试样的应变-时间关系曲线，如图1 所示(其中Z表示生物酶掺量；ε表示试样应变；t表示作用时间.) .

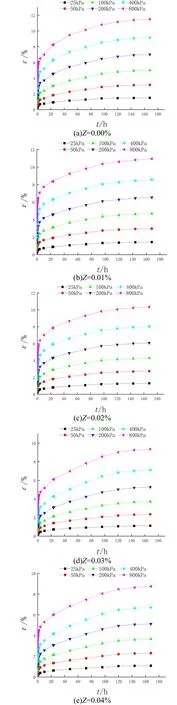
图1 ε-t 关系曲线

由图1 可知：1)随着生物酶掺量的增加，土体总压缩变形量逐渐减小，土体强度增加；2)刚开始施加荷载时试验土体会产生瞬时的弹性变形，在恒定持续荷载下，土体缓慢变形；3)在低荷载(25 和50 kPa)作用下，不同生物酶掺量的有机质土ε-t关系曲线平直，次固结特性不明显；在高荷载 (100、200、400 和800 kPa)作用下，不同生物酶掺量的有机质土ε-t关系曲线斜率较大，次固结特性较明显.

2.1 结构屈服应力的确定

王国欣等[21]认为先期固结压力适用于非结构性土，对于重塑结构性土则应该用结构屈服应力来描述.郝玉龙等[22]提出了一种确定结构屈服应力的新方法.文献[23-25]提出可由ln(1+e)-lgP双对数曲线关系确定结构屈服应力，即2 直线的交点为结构屈服应力.Hong 等[25]和Onitsuka 等[26]通过大量的试验数据验证了该方法的有效性.鉴于此法简单，适用性强，笔者亦采用ln(1+e)-lgP双对数曲线关系得到了结构屈服应力，如图2 所示.由图2 可知，不同生物酶掺量下试验土体的结构屈服应力大致在100 kPa.

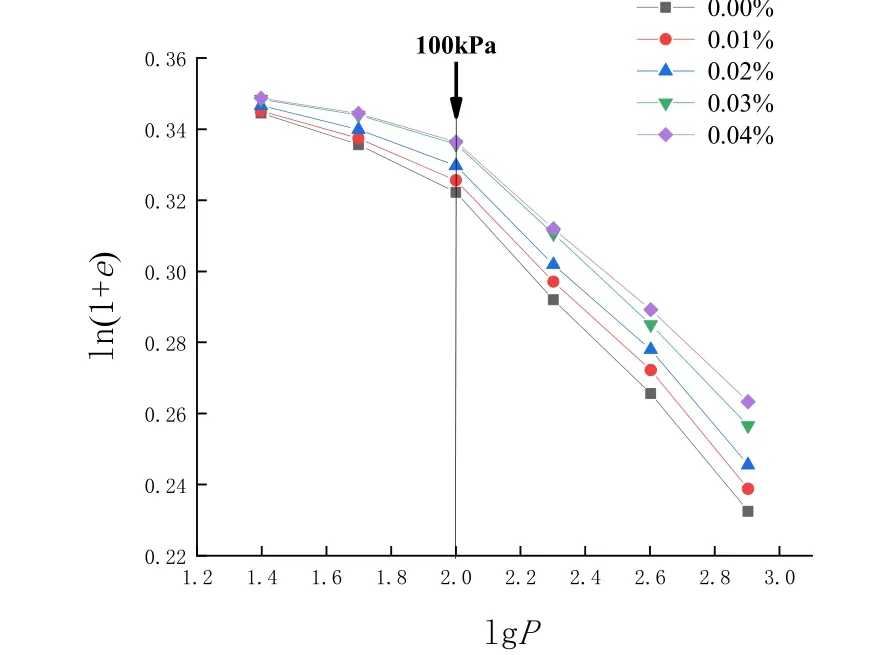
图2 不同生物酶掺量下ln(1+e)-lgP 关系曲线

2.2 不同生物酶掺量下次固结系数与荷载关系

Buisman 提出的由e-lgt关系曲线确定次固结系数的方法：Ca=-Δe/(lgt2-lgt1)，得到了广泛使用.由该式可知次固结系数与压力无关[27].不同生物酶掺量下各级荷载的次固结系数如图3所示.由图3 可知，在较高荷载下生物酶掺量为0.01%时，次固结系数最低；次固结系数随荷载的增加出现了峰值(约在100 kPa 处)，且其峰值一般出现在结构屈服应力附近[28]；当P为25～200 kPa 时，次固结系数随荷载增加变化明显；当P超过200 kPa 时，次固结系数变化平缓.由此可知，当荷载小于结构屈服应力时，次固结系数与荷载呈正相关性；当荷载等于结构屈服应力时，次固结系数达到峰值；当荷载大于结构屈服应力时，次固结系数与荷载呈负相关性.

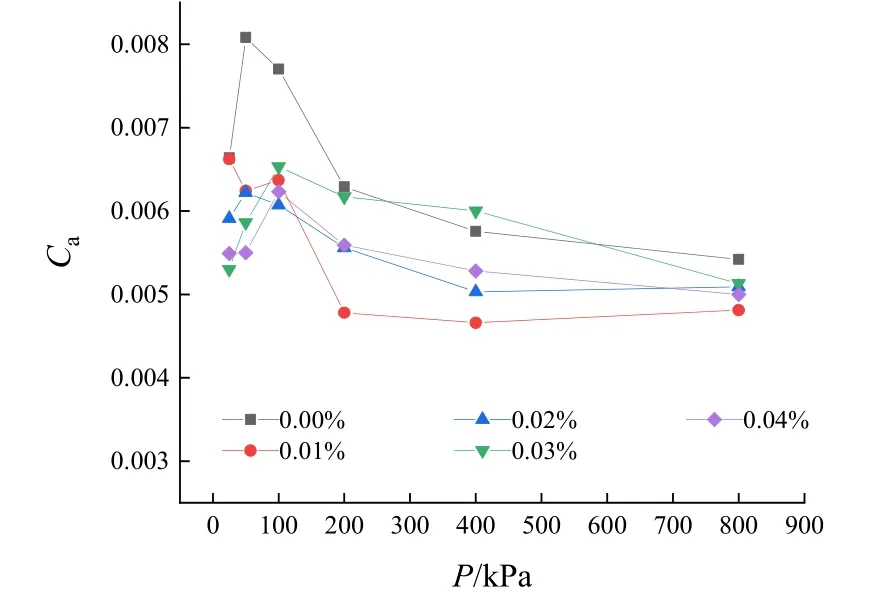
图3 不同生物酶掺量下次固结系数与荷载关系

3 一维次固结模型的建立

为了描述土体本构模型物理量间的关系，常用的物理方程有双曲线、对数和指数函数.笔者采用双曲线模型来描述一维次固结，其方程如式(1)所示.

其中，A为ε-t关系曲线初始斜率E的倒数；B为ε-t关系曲线最终应变dε的渐近线的倒数.参数E和dε可根据实测的ε-t关系曲线确定，即双曲线模型的2 个参数，E～P与εd～P的关系曲线如图4 所示.

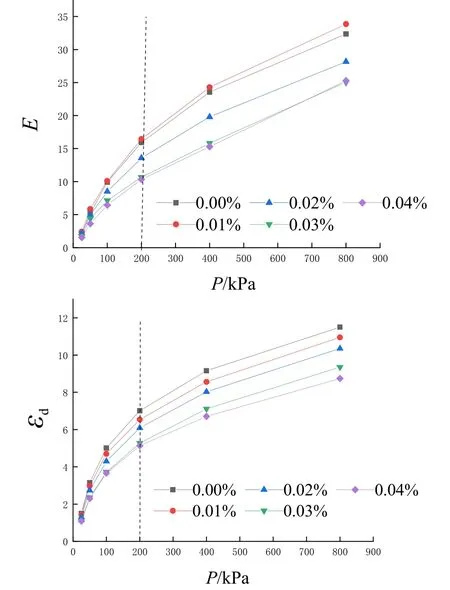
图4 不同生物酶掺量下 E～ P、 εd ～P关系

由图4 可知：1)E～P、εd～P的关系曲线在P=200 kPa 处有明显的拐点；2)当荷载小于等于200 kPa 时，E与dε随荷载P的变化较明显；3)当荷载大于等于200 kPa 时，该变化趋于平缓.

目前，国内外学者研究结构屈服前后的土体次固结特性较少，故本文将针对结构屈服前后土体的次固结特性进行研究.对于屈服前阶段与屈服后阶段，E～P与εd～P的关系呈现良好的幂函数关系，其方程式为

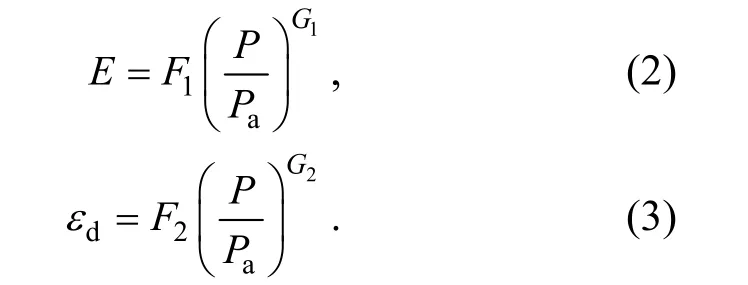
其中，Pa为标准大气压强，Pa≈101.325 kPa；F1、F2为幂函数系数；G1、G2为幂函数指数.

根据E～P与εd～P的关系曲线拟合各参数，所得结果见表2～表3(其中Z为生物酶掺量).

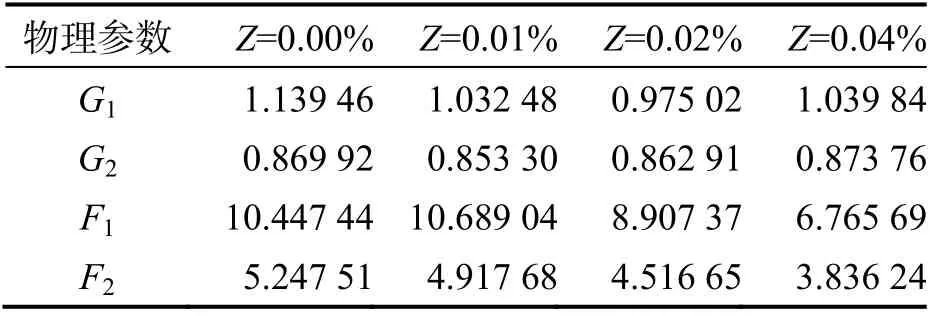
表2 屈服前阶段的拟合

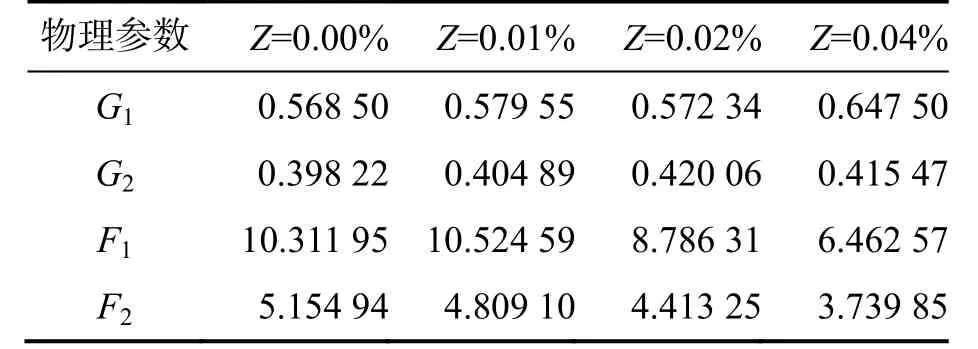
表3 屈服后阶段的拟合

从表2 和表3 可知：1)在相同生物酶掺量下的土体屈服前阶段与屈服后阶段，其F1与F2变化不大；2)G1与G2在屈服前阶段的值普遍大于屈服后阶段的值；3)F1与F2随着生物酶掺量的增加而减小，G1与G2则同生物酶掺量关系不大.

基于此，式(1)可改写为

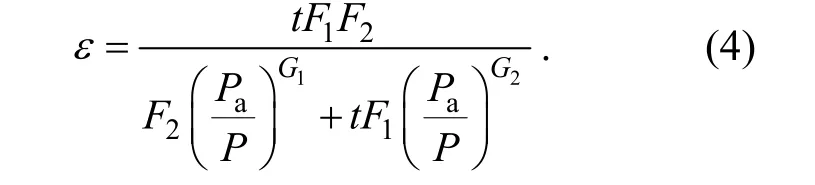
对模型参数与试样生物酶掺量间的关系进行回归分析，确定两者的经验关系式分别如公式(5)～公式(12)所示.

屈服前阶段：

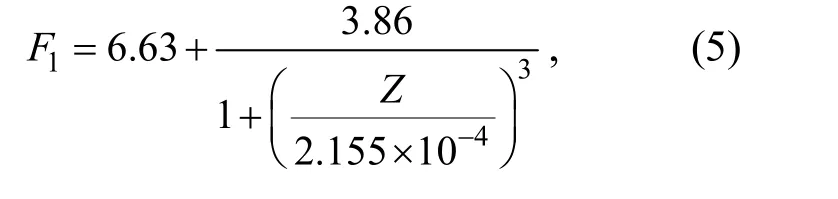
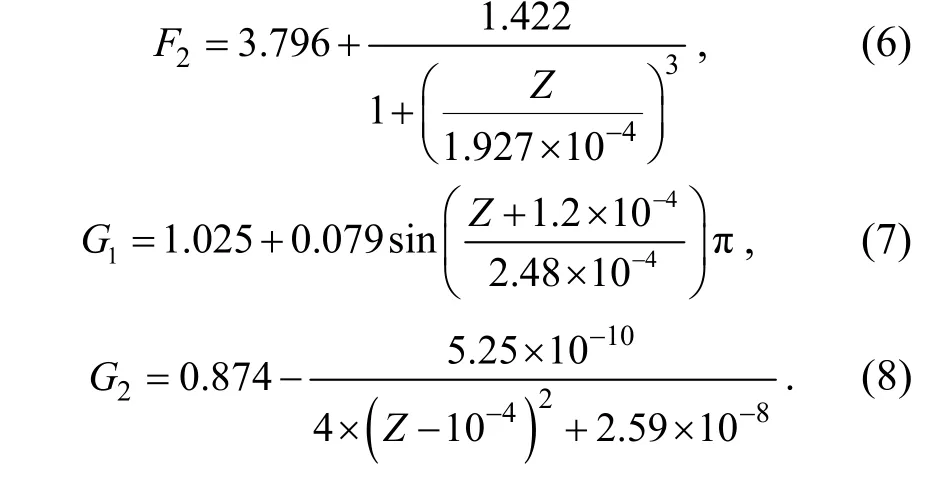
屈服后阶段：

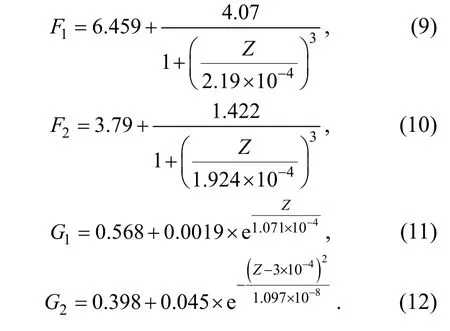
4 模型验证

利用式(5)～式(12)预测当生物酶掺量为0.03%时改良有机质土的应变-时间关系，其预测值与试验值对比结果见图5.由图5 可知，试验值与预测值吻合度较高，这说明了模型的有效性.

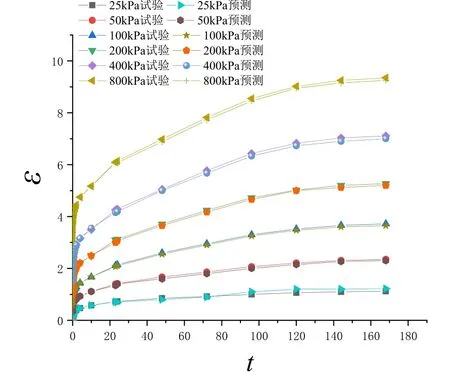
图5 生物酶改良有机质土的ε-t 关系验证(Z=0.03%)

5 结论

1)生物酶改良有机质土结构屈服应力约为100 kPa，其次固结系数随荷载增加出现峰值，该峰值约在荷载为100 kPa 时出现；当荷载小于该结构屈服应力时，土体次固结系数与荷载呈正相关性；当荷载大于结构屈服应力时，其次固结系数与荷载呈负相关性.

2)随着生物酶掺量的增加，改良土体总压缩变形量逐渐减小.在低荷载下，不同生物酶掺量有机质土的ε-t关系曲线平直，次固结特性不明显；在高荷载下，其ε-t关系曲线斜率较大，次固结特性较明显.

3) 通过建立生物酶掺量与模型参数的经验关系式，并利用其对改良土体的变形量进行预测，发现试验值与预测值吻合度较高，验证了模型的有效性.