基于信息论的施工会议效率提升策略

刘宁宁，刘 敏,2,*，苗吉军，王志高，张玉香

(1.青岛理工大学 土木工程学院， 青岛 266525；2.北卡罗莱纳州立大学 土木及环境工程系，北卡 罗利 27616)

建筑业历来在国民经济发展中占有重要地位。但是建筑项目在完成造价和工期方面的总体表现并不理想。在过去的20年里，在同期世界经济年增长率2.8%的大环境下，建筑工业的劳动生产率平均年增长仅有1%，远远落后于3.6%的制造业的平均年生产率增长率[1]，在先进科学技术发展日新月异的时代，为什么建筑项目的表现不进反退？如何才能有效地计划和协调工程项目进度以提高生产率，减少浪费和对国计民生带来的负面影响？在熟练技术工人短缺，劳动力成本日益高涨的今天，对这些问题的研究迫在眉睫。

长期以来，建筑项目管理的研究聚焦在正式的合同和组织管理层面。研究集中在自上而下的正式项目合同管理和时间进度管理工具的开发。这种管理概念基于的假设是只要上层管理计划明确下达，现场管理人员与施工工人就应该按照计划准确可靠地执行并完成。而事实上，施工计划和执行充满了不确定性和互相关联性，它对建设成本和工期的影响在很大程度上是取决于基层的沟通和决策。而沟通决策的一个重要途径就是施工会议，项目管理人员需要花费大量的工作时间在各种规划会议上，与各种利益相关者进行沟通和协商，包括业主、设计师、监理、供应商、地方市政当局及多个分包商。他们需要在施工会议中考虑并消除至少七种约束条件，这七种约束条件分别是:1)设计和工作方法；2)材料；3)劳动力；4)设备和工具；5)工作空间；6)前道工序；7)外部条件[2]。通过消除这七种约束来提高工作流的可靠性，因为建立可靠的工作流是提高建筑劳动生产率的关键。

如何在有限的会议时间内针对这七种约束条件有效地讨论、协调和计划是施工管理人员每天都要面对的问题。建设施工管理人员通常需要花费大量的时间参加计划会议的讨论。但是缺乏关于如何通过提高计划会议的信息交换效率来提高工作计划完成的可靠性的指导。本研究的目的是：1)量化各约束信息所含的不确定性；2)量化规划会议中各约束对计划可靠性的影响，即信息传递效率；3)提出提高会议有效性的指导方针，以提高计划的可靠性。本研究收集了一个大型写字楼项目的200多项生产计划和生产数据及22个项目管理人员参与的13周详细的周会议记录，使用信息论法对会议中的信息交换不确定性、交换量和信息分享进行了定量分析。这些研究结果将帮助项目管理人员清晰地认识到关于去除约束条件的讨论是如何影响任务完成度的，从而可以根据有效性来安排会议内容的次序及重点，将施工会议进行得更有效率进而提高生产率。

1 施工计划完成可靠性和约束条件

本文采用施工计划完成百分比, Percent Plan Completion (PPC)，作为一个测量施工计划完成可靠性的有效指标，PPC是100%完成的任务数量与所计划的总的任务数量的比率[3]。例如某钢筋工安装班组计划在一周内完成20根柱筋绑扎，实际100%完成15根柱筋绑扎，50%完成3根柱筋绑扎，另外2根柱筋完全未开始，这个班组的PPC是75% (15/20)。PPC 是一个有效地衡量计划任务完成可靠度的指标，因为只有100%完成的工作任务才能使得下一个班组顺利开始另一项后续工作。研究也发现PPC与生产率有正显著相关性[4]。JANG等通过分析两个桥梁建设项目数据的约束消除率和PPC发现两者之间存在着显著的正向关系[5]。所以PPC的提高对提高生产效率非常重要。在这里对PPC的分组采用K-means分组方法，也叫k均值聚类算法，是一种迭代求解的聚类分析算法，其步骤是：预将数据分为k组，则随机选取k个对象作为初始的聚类中心，然后计算每个对象与各个种子聚类中心之间的距离，把每个对象分配给距离它最近的聚类中心，聚类中心以及分配给它们的对象就代表一个聚类。这种分类方法的最大特点就是基于数据自身的分布特点将其分类，因此很适用对PPC进行分类，k可以根据需要进行设置，在本研究中，设k等于3，将PPC按高、中、低分为3组。

KOSKELA提出为了保证施工任务的顺利和高效的完成，管理者需要计划和准备7个内部和外部的约束条件[2]。LINDHARD等通过三个住宅案例研究，分析了约1280个挖掘和翻新等施工活动中经常面临的一些问题和任务未完成的原因，发现不安全的工作条件和未知的工作条件是未完成任务的潜在原因[6]。在最近的一项研究中，HAMZEH等通过分析计算机模拟和使用任务就绪的过程表明，在施工活动准备就绪过程中识别和消除约束会提高计划的可靠性和缩短工期的重要性[7]。但是他们没有调查在每天或每周规划会议中约束移除信息的获取和传递，以及它是如何影响PPC的。鉴于此，本文采用KOSKELA提出的7个施工计划的关键约束条件，分析在施工计划会议讨论中关于这7个约束条件的信息是如何交换和传递的，从而提出帮助管理者有效提高施工计划会议讨论效率的策略和方法。

2 信息理论

信息理论是SHANNON提出的一个完整的理论框架，用来定量测量数据值分布中的信息(或不确定性)内容[8]。近年来，信息论在各个领域的应用呈上升趋势，包括：医学科学、生物力学、建筑与土木工程[9]。在建筑与土木工程领域，信息理论主要用于风险分析和结构分析，例如，GE等将熵度量方法应用于建筑系统的风险评估[10]。

虽然信息理论已经被尝试应用于土木工程和施工管理中[11]， 但目前国内还没有将信息论方法应用于施工会议效率的研究实例。为了测量变量产生的信息量，本文引入了SHANNON的熵H(X)，计算公式如下：

(1)

式中：H(X)为熵，代表X变量中包含的不确定性，bits；X为离散的随机变量，可以取xi的m个可能的结果；p(xi)为随机变量X取xi的概率，xi∈{x1,x2,…,xm}。

对任意一个有两种可能值的变量来说，在不确定性最高的情况下，也就是当每种取值的可能性都是50%时，熵达到可取的最大值为1。例如抛硬币，会有两种结果，可能性各50%，代入式(1)，H(X)熵的值就是1。相反，当取一种值的可能是100%，取另一个值的可能是0，也就是说完全确定的情况下，H(X)也就是熵的值是0。所以熵H(X)衡量一个随机变量所含的不确定性，熵的值越大，不确定性越大。

为了确定一个变量与另一个变量共同含有的信息量，本文使用信息论中的如下公式计算相互信息I(X,Y)：

(2)

式中：X和Y为两个离散的随机变量，可以分别取mx，my个可能的结果；p(yj)为随机变量Y取yj时的概率值；p(xi,yj)为X和Y的联合概率。

相互信息也可以通过式(3)计算：

I(X,Y)=H(X)+H(Y)-H(X,Y)

(3)

其中，

(4)

相互信息是两个变量之间关联的一般测度[12]，它衡量的是对其中一个变量在了解多大程度上能够减少对另一个变量的不确定性，这样可以量化变量间信息传输的效率，信息传输效率P可以用以下公式计算：

(5)

式中：H(X)为关于变量X所产生的不确定性的信息量，bits；I(X,Y)为关于变量Y给变量X的信息量，bits。

3 方法

建筑施工计划会议的关于施工任务7个约束条件的讨论，其数据包含的特征有： 1)每个约束条件的讨论在每次计划会议中出现的概率不确定；2)各个约束条件的讨论可能有相关的内容，比如当材料供应不足时，工人的工作时间也会受限；3)关于约束条件的讨论会影响到施工任务完成的可靠度PPC。图1显示了本文的研究设计，前两组数据，每周计划会议记录和每周展望计划，是从研究案例的项目会议记录中收集的，并进行了研究和分类，以确定在会议期间关于每个约束条件讨论的频率。采用前瞻性规划和结果法计算生产能力，计算PPC值后，将PPC值按K-means方法分为高中低三组。然后对每个约束类别依据式(1)(2)(5)进行信息的不确定性和信息传输效率的计算。最后，提出提高会议效率措施，以实现更高的PPC。

4 案例描述

本文以青岛某在建大型写字楼为研究案例。该项目的主塔楼部分包含了典型和重复的活动，这些活动在整个项目的工作复杂性方面具有可比性。该项目规划为地上43层、地下3层，预计造价7.25亿元，工期从2018-08-17—2021-01-22，预计历时890 d，本研究的范围是主塔楼2—16层的墙钢筋绑扎、钢结构梁柱吊装、升爬模、模板施工、板钢筋绑扎、埋设线管、混凝土浇筑等施工活动，调查持续时间为13周。该项目有三周的前瞻性计划，每周的计划会议都会更新计划。

4.1 周计划会议

在该项目中，会议在每周一晚上6:10准时举行，会议平均时间为98 min，最短76 min，最长130 min。参加会议的人数从10人到21人不等，平均为13人，参加者包括一名项目经理，一名生产经理，一名项目总工，一到三名商务部门人员，二到三名物资部门人员，一到二名资料员，二到三名安全员，二到四名现场土建工程师，一名钢结构工程师，一到二名BIM工程师。在这些会议中，参会者讨论了与这七项施工活动相关的施工进度、施工计划以及其他主要活动。会议还讨论了项目的一般情况和其他事项(如安全、合同文件、场地布局等)。会议记录是描述性的，包含了所有会议期间关于7个约束条件的讨论，总共记录了90天273页的会议详情。所有13周的会议记录都是由同一个人记录的，保证了记录的可比性。记录者从第一天开始就参加了所有的会议。在仔细审阅会议记录后，笔者将与主楼相关的七项施工活动的讨论项目分为前面所提到的7个约束类别。

4.2 PPC的计算和分类

本项目每周五更新前瞻计划，展示当前周和前一周七项施工活动的实际开始时间和实际完成时间。此外，前瞻计划包含了计划的开始时间和未来三周七项施工活动的完成时间。本文采用PPC作为计划可靠性的度量指标，计算公式如下：

(6)

式中：K表示PPC；L为按计划完成的任务数量；H为计划总的任务数量。

区分计划的可靠性。使用K-means聚类算法将PPC分为低(L)、中(M)和高(H)三组。K-means试图将PPC划分为K个簇(K由用户定义)，其中每个PPC都属于具有最接近平均值的簇。选择K-means聚类算法的原因是算法是非重叠算法，PPC被按照自身的分布特性分为三个聚类。

4.3 信息的不确定性和信息传输效率

通过以下步骤计算熵和信息的不确定性，用于约束讨论：

1) 根据7个约束条件对会议进行分类，并将每次会议对每个约束条件的讨论频率记录到X1到X7的离散变量中，其中X1=外部条件，X2=设备可用性，X3=劳动力可用性，X4=材料可用性，X5=前道工序，X6=空间可用性，X7=设计和工作方法。(表1，第2—8列)。将PPC分类为L，M或H (低、中、高)，并将数据记录为离散变量Y(表1，第9—10列)。

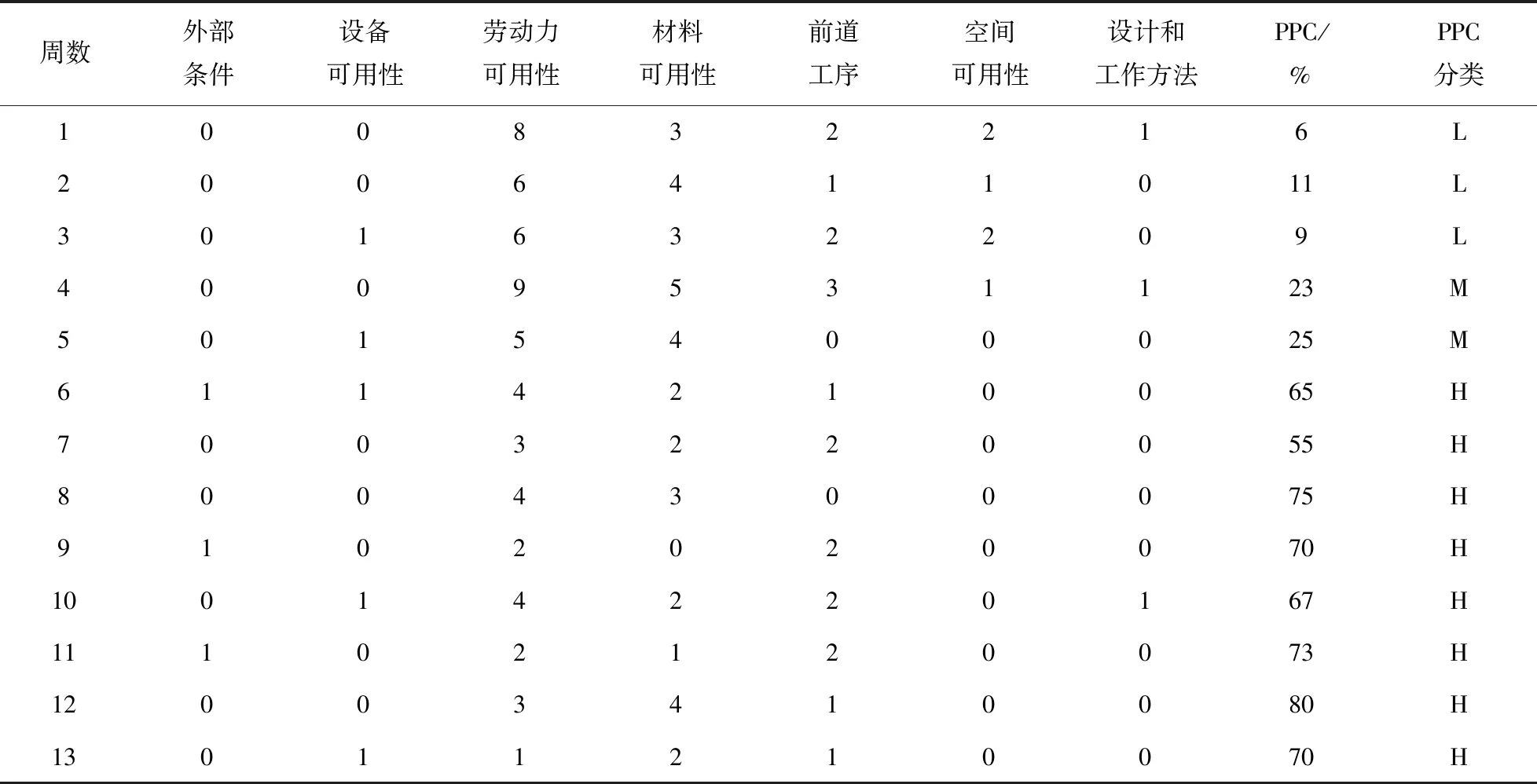
表1 约束移除讨论和PPC分类

2) 在每个X和Y之间生成一个交叉选项卡。每个交叉选项卡以二维矩阵格式显示X变量相对于Y变量的分布。交叉选项卡中的行是会议中讨论约束条件的频率(即一次、两次、三次等)，列是PPC级别(即L，M或H)。

3) 在前面步骤中创建的交叉制表符中添加一行和一列，并插入步骤2中生成的交叉制表符的行和列的和。

4) 计算联合和边缘概率，将步骤3中交叉标签的每个单元除以总和。

5) 对步骤4中的概率取以2为底的对数。

6) 用式(4)计算联合熵和边际熵。

7) 利用式(1)计算每个X和Y的熵。对步骤6计算的边际熵求和。

8) 根据步骤6和步骤7的结果，利用式(3)计算相互信息。

9) 根据步骤7和步骤8的结果，使用式(5)计算信息传输效率。

5 结果和讨论

在表2中，H(X)表示约束类别产生的信息量；H(Y)表示PPC中的不确定性或消除PPC中的不确定性所需要的信息量，其不确定性来自于下周PPC的不可预测性，它有可能是L，M或H；I(X,Y)是给定约束信息下关于PPC所获得的信息量；I(X，Y)/H(X)为约束与PPC之间的信息传递效率。例如，“前道工序X5”生成的信息量为1.738 bits，“空间可用性X6”生成的信息量为1.198 bits，几乎是“空间可用性X6”生成的信息量的1.5倍。但是这两种约束关于PPC所获得的信息量中，后一种约束类别X6的信息量是前一种约束类别X5的1.64倍。X6的信息传输效率几乎是X5的2.4倍(0.694∶0.292)。

表2 周例会信息获取与传递效率

由表2可知， PPC有1.335 bits的不确定性。因此，为了消除不确定性，需要获得1.335 bits的信息。从约束去除讨论中可以得到总信息是I(X,Y) =3.71 bits，大于PPC中的不确定度。表2最后一列表示的是信息传输效率，可以看出“设备可用性”这个约束条件的信息传输效率最低，在实际工程中，管理人员对“设备可用性”的信息交换也特别不敏感，开施工会议时在此约束条件中花费的精力很少，有时发生设备突然不能正常运转导致工程部分停工而措手不及，所以建议管理人员应该经常和设备租赁单位勤沟通，对设备实时动态掌握其可用性，这将有效避免一些不必要的停工。

图2显示了通过将每个约束条件的I(X,Y)除以7个约束条件总的I(X,Y)来计算关于某个约束条件信息缺失导致的对计划可靠性的风险。从图中可以看出，对于PPC的提高贡献最大的三个约束类别是“劳动力可用性”“空间可用性”和“材料可用性”。

在图3中，横坐标x表示信息的不确定性，x值越大，表示信息的不确定性就越大；纵坐标y表示对计划可靠性的影响，y值越大，表示对计划可靠性的影响就越大，根据这些信息可以将该图进一步划分为四个区域。在图3的第一个区域，表示该区域的约束不仅有很高的不确定性，而且对计划的可靠性影响也很大；在其第二个区域，表示该区域的约束信息的不确定性很低，但是对计划可靠性的影响很大；在其第三个区域，表示该区域的约束信息的不确定性很高，但是对计划可靠性的影响很小；在其第四个区域，表示该区域的约束信息的不确定性很低，对计划可靠性的影响也很小。明确了这些，图3可以为每次会议中讨论约束条件的优先级提供了基础。在第一个区域，约束对于PPC的提高是很重要的，并且需要被有效的讨论，因此，这方面的约束条件(X3和X6)在会议讨论中具有最高的优先级。在第二个区域，尽管它们不需要被有效的讨论，但其对于PPC的提高很重要，因此，这方面的约束条件应以较少的努力简明扼要地加以处理即可，并在会议上作为第二优先事项加以讨论，当然在本项目中没有发现这个区域的约束。在第三个区域，约束对于PPC的提高虽然不是很重要，但是它们需要被有效的讨论，因此，这个区域的约束(X4)需要付出更多的努力来解决，并且作为第三个优先级讨论。最后，在第四个区域，约束对于PPC的提高不仅不重要，而且也不需要被过多的讨论，因此，这个区域的约束条件(X1，X2，X5和X7)在会议中讨论的优先级最低。以这种方式确定约束讨论的优先级将确保在有限的会议时间内获得更多关于PPC提高的信息。

6 结论

本文以青岛某在建大型写字楼工程为例，运用信息理论分析了在施工计划会议中信息交换和传输的效率，提出了帮助项目管理人员根据约束讨论的优先级来提高计划会议的效率的建议，从而达到更高的计划有效性。该研究方法可以推广应用于类似的施工项目对约束进行分析，并得出该约束的信息不确定性及对计划可靠性的影响，并作出类似图3的优化图，在每周计划会议中解决与约束讨论排序相关的问题，从而指导施工。

本文的局限性在于由于时间的限制，分析仅仅基于一个项目，未来的研究可以基于多个项目用类似方法进行分析。