地下连续墙成槽施工槽壁稳定时空效应的分析

王晓华 贾文彪 胡长明 路 乾 杜逸璞

(1.中铁一局集团建筑安装工程有限公司,西安 710055；2.西安建筑科技大学土木工程学院,西安 710055；3.陕西省岩土与地下空间工程重点实验室,西安 710055)

近年来，城市轨道交通发展迅猛，大批地铁车站开始兴建，随之而来的深基坑也不断涌现，并且不断地朝着“更大、更宽、更深”的方向发展[1-2]。地下连续墙作为基坑支护形式的一种，有着刚度大、整体性好等优点，特别适用于敏感环境下变形控制和环境保护要求较高的基坑工程[3]，但由于地下连续墙深度较大，成槽过程中容易发生槽壁土体剥落、坍塌等现象，造成工程事故，因此槽壁稳定性一直是工程界重点关注的问题。

目前针对槽壁稳定性问题，不少学者做出了一些有意义的研究。夏元友等基于二维楔形滑块模型，提出了考虑土体分层的槽壁稳定水平条分法[4]。曹豪荣等通过对文献、资料调研，对槽壁失稳破坏模式及相应的理论分析方法进行了归纳总结[5]。罗爱忠等利用有限差分法，对地下连续墙成槽施工过程中槽壁应力和变形进行了数值分析[6]。秦会来等基于ABAQUS有限元软件，采用修正剑桥土体本构模型，分析了成槽施工诱发地层变形的特点及相关影响因素[7]。丁勇春等通过对成槽施工的现场监测数据分析，得到了槽段分段开挖、泥浆持荷时间及泥浆压力对槽壁土体侧移和地表沉降的影响[8]。此外还有不少针对异形槽段或特殊条件下的槽壁稳定性分析[9-13]。但上述研究多集中在理论失稳机制、数值模拟及现场实测方面，并没有深入研究槽壁稳定性的时空效应。

因此，从不同施工阶段槽壁土体应力状态出发，对槽壁稳定性影响因素进行探讨，重点分析开挖瞬时槽壁土体稳定性的时空效应，并结合现场实测数据证明时空效应对槽壁稳定性的影响作用，最后提出一系列有针对性的保证措施。

1 槽壁土体应力分析[14]

地下连续墙成槽可视为槽深范围内土体瞬时卸荷过程，对于槽壁土体单元而言，其应力状态会随成槽开挖过程而改变，图1所示为槽壁单元土体M的应力分析简图。为便于分析，取泥浆液面和地下水位均与地面平齐，q为地面均布荷载，σ1和σ3分别为单元体M受到的竖向应力和水平向应力。根据地下连续墙成槽施工过程，槽壁单元土体M依次经历开挖前初始平衡、开挖瞬时以及开挖之后三种不同的应力状态，各阶段应力状态分别用σb、σn、σa表示。

图1 槽壁单元土体M应力状态Fig.1 The stress state of soil element M

成槽施工前，在地面均布荷载作用下槽壁土体处于初始K0应力平衡状态，单元土体M应力状态表示如下：

总应力：

σb1=γ′z+Kcq+γwz

(1a)

σb3=K0(γ′z+Kcq)+γwz

(1b)

有效应力：

(1c)

(1d)

式中：γ′为土体浮重度；γw为水的重度；γs为泥浆重度；K0为静止土压力系数；Kc为附加应力系数;z为单元土体M的深度。

成槽开挖后，单元土体M应力状态为：

总应力：

σa1=γ′z+Kcq+γwz

(2a)

σa3=γsz

(2b)

有效应力：

(2c)

(2d)

可见，成槽开挖打破了槽壁土体原有的初始平衡状态，引起了应力重分布。成槽开挖前、后单元土体M总应力差为：

Δσ1=0

(3)

Δσ3=(γs-γw)z-K0(γ′z+Kcq)

(4)

由Skempton建议的超静孔隙水压力增量表达式(式(5))可得槽段开挖引起单元土体M孔隙水压力变化为：

Δu=B[Δσ3+A(Δσ1-Δσ3)]

(5)

式中：A、B均为孔隙水压力系数，对于饱和土，B=1。

将式(4)代入式(5)得：

(6)

由此可得槽段开挖瞬时单元土体M有效应力状态为：

K0(γ′z+Kcq)]

(7a)

K0(γ′z+Kcq)]

(7b)

由上述分析可得槽壁单元土体有效应力路径如图2所示，其中A′圆为初始有效应力圆，B′圆为槽段开挖瞬时有效应力圆，C′圆为槽段开挖后有效应力圆，B′、C′圆半径相同，圆心位置相对距离为Δu，在槽壁周围有均布荷载的情况下，对于正常固结土和超固结土而言，1-A>0，而一般情况下(γs-γw)z-K0(γ′z+Kcq)<0，故Δu<0，即在槽段开挖瞬时会产生负的孔隙水压，有利于槽壁稳定，随着时间推移，负孔隙水压慢慢消散，单元土体应力路径逐渐趋于极限破坏线，此时对于槽壁是不利的，因此在成槽结束后应尽快吊装钢筋笼、浇筑混凝土维持槽壁稳定，避免因施工间歇过长导致槽壁失稳。

图2 单元土体有效应力路径Fig.2 The effective stress path of soil elements

2 槽壁稳定条件

进一步分析图2可得超载条件下槽壁开挖瞬时的稳定条件为：

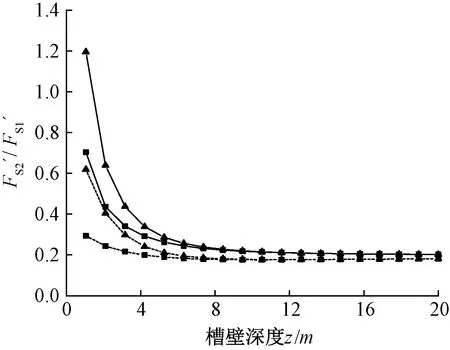
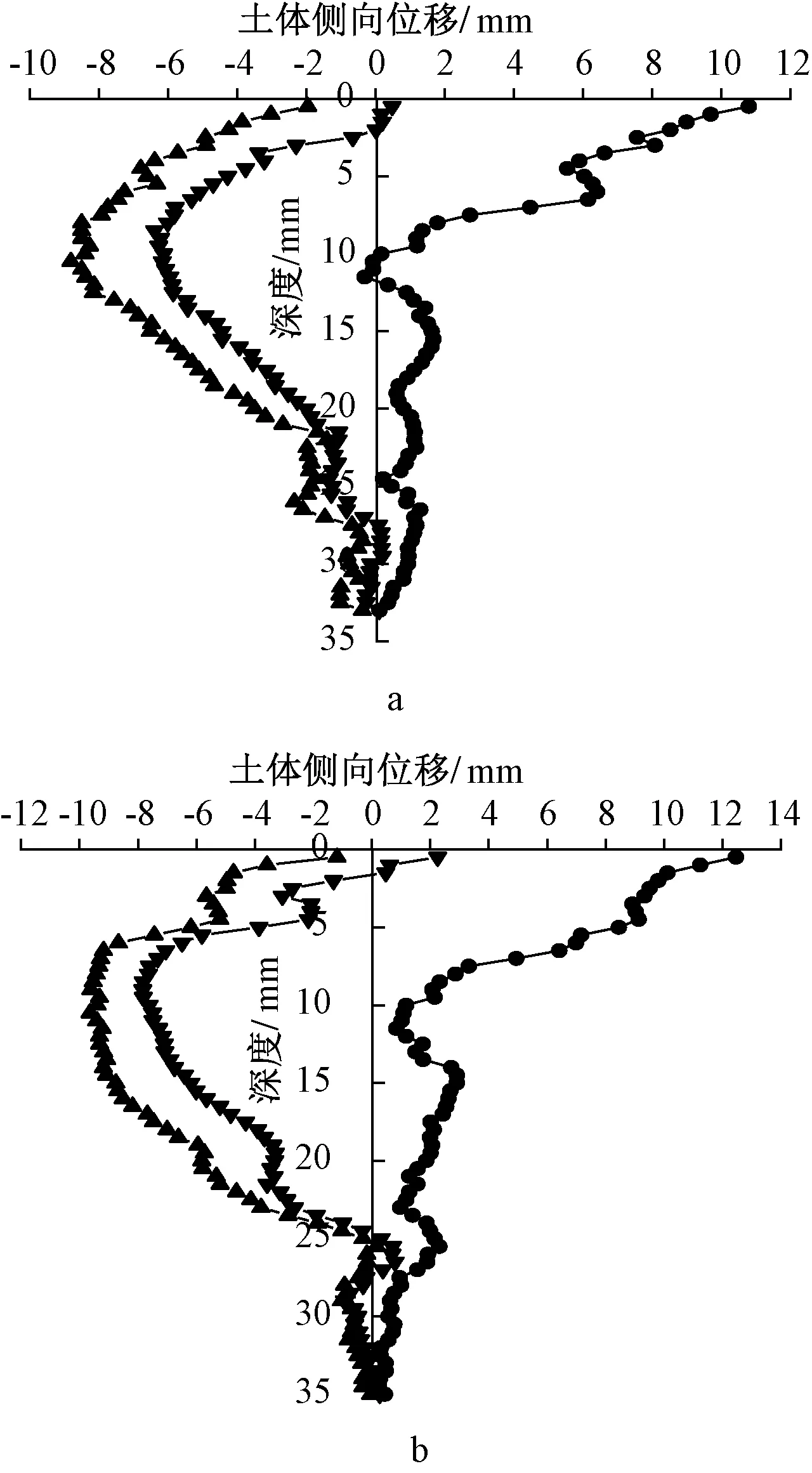
θ<φ′或sinθ

(8)

式中：φ′为有效应力状态下土的内摩擦角。

而sinθ又可表示为：

[γ′-(γs-γw)]{γ′+(γs-γw)+

2(1-A)[K0γ′-(γs-γw)+K0Kcq/z]}-1

(9)

此时槽壁稳定安全系数Fs可表示为：

(10)

3 槽壁稳定性时空效应

将式(10)右边分解为两项，即：

Fs=Fs1+Fs2

(11)

式中：Fs1为基本稳定系数；Fs2为时空稳定系数。

(12)

(13)

3.1 基本稳定系数Fs1

进一步分析式(12)得到基本稳定系数Fs1与土体有效内摩擦角φ′及泥浆重度γs的关系曲线如图3所示。取γ′=9.0 kN/m3，γw=9.8 kN/m3，由图3可得:基本稳定系数随土体有效内摩擦角及泥浆重度增大而增大，并且当土层条件一定时，基本稳定系数的增幅会随泥浆重度增大而不断增大，例如：当φ′=30°时，泥浆重度以增量1 kN/m3从10 kN/m3增大到13 kN/m3，对应基本稳定系数Fs1的增幅分别为25%、26.15%和28.05%，虽然增大泥浆重度可以适当提高槽壁稳定性，但较大的泥浆重度会降低成槽速度，并且会增大泥浆制备和回收利用的难度，因此实际施工中一味增大护壁泥浆重度提高槽壁稳定性的做法并不可取。

— φ′=20°;— φ′=30°;— φ′=40°。图3 Fs1与φ′及γs的关系曲线Fig.3 Relations of Fs1，φ′ and γs

泥浆护壁的基本原理是利用泥浆侧向压力平衡槽壁土压力和静水压力，从而保证槽壁稳定，为增大泥浆侧向压力，除增加泥浆重度之外，提高泥浆液面也能达到这一效果。图4为泥浆液面提高后槽壁泥浆压力的分布示意，此时槽壁单元土体水平方向有γsh(h为泥浆液面超出地下水位的高度)的增量，而竖直方向应力状态不变，于是可得到：

(14)

(15)

超高泥浆压力增量；无超高泥浆压力。图4 超高泥浆液面高度时泥浆压力分布Fig.4 Slurry pressure at an ultra-high slurry level

由式(14)可得：当提高泥浆液面后，基本稳定系数Fs1与槽壁深度z密切相关，取γ′=9 kN/m3，γs=11 kN/m3，γw=9.8 kN/m3，得到基本稳定系数相对增量随槽壁深度变化规律如图5所示。分析图5可得：提高泥浆液面对浅层土体的影响远大于深层土体，在z=2h处，基本稳定系数提高了4.7倍，z=4h处为1.9倍，z=8h处为1.3倍。可见，提高泥浆液面总体效果大于增大泥浆重度。实际施工中通常要求泥浆液面必须高出地下水位0.5 m以上。

3.2 时空稳定系数Fs2

对于时空稳定系数Fs2，由于Δu=(γs-γw)z-K0(γ′z+Kcq)<0，式(13)又可表示为：

(16)

由式(16)得出：时空稳定系数Fs2的实质是槽深范围内土体侧向卸荷引起负的孔隙水压力，当负孔隙水压力Δu随时间慢慢消散，槽壁稳定性便逐渐减小。Δu不仅受泥浆重度影响，而且与土体孔隙水压力系数A、静止土压力系数K0及地面超载q密切相关。假设槽壁土体为正常固结土，取孔隙水压力系数A=0.75，土体有效内摩擦角φ′=25°，则静止土压力系数K0=0.58，此外同样取γ′=9 kN/m3、γs=11 kN/m3、γw=9.8 kN/m3，此时时空稳定系数Fs2可表示为：

泥浆液面无超高时：

Fs2=0.02Kcq/z+0.11

(17)

泥浆液面超高时：

(18)

m=l/b

n=z/b

式中：Kc为附加应力系数[15]；l为矩形荷载长边；b为矩形荷载短边；z为槽壁深度。

图关系曲线Fig.5 Relations between and z/h

以图6所示槽壁土体破坏模式为例，计算得到滑动体宽度B为：

图6 槽壁土体破坏模式Fig.6 The failure mode of the trench

B=Hcrcotθ

(19)

将Hcr=Lsinθ/(2tanφ′)[16]代入式(19)并整理得：

(20)

以长为6 m的单幅槽段为例，依据塑性极限破坏理论取破裂角θ=45°+φ′/2，由式(20)可得其矩形荷载施加范围为6.00 m×3.46 m。取地面超载q=75 kPa，得到槽壁中点及两端土体单元时空稳定系数Fs2随槽壁深度z的变化曲线如图7所示。

— h=0 m,槽壁端点；— h=0 m,槽壁中点；----- h=0.5 m,槽壁端点；----- h=0.5 m,槽壁中点。图7 Fs2-z关系曲线Fig.7 Relations between Fs2 and z

由图7可得：槽壁中点及两端土体单元时空稳定系数Fs2随槽壁深度z的变化规律相同，即随槽壁深度的增大不断减小至趋于定值，并且成槽对浅层土体的扰动程度在时空效应方面要大于深层土体，进一步对比分析发现，泥浆液面超高对时空稳定系数的影响随槽壁深度的增大逐渐削弱。此外，超载条件下槽壁中点处的浅层土体相较于槽段端部更容易受成槽施工的影响。

3.3 槽壁稳定时空效应分析

将式(16)、(15)相比得：

(21)

— h=0 m,槽壁端点；— h=0 m,槽壁中点；----- h=0.5 m,槽壁端点；----- h=0.5 m,槽壁中点。图关系曲线Fig.8 Relations between and z

上述分析都是建立在无黏性土的基础之上，对于黏性土而言，槽壁开挖瞬时土体单元应力状态如图9所示，此时槽壁稳定安全系数Fs可表示为：

图9 槽段开挖瞬时黏性土体单元应力状态Fig.9 The stress state of viscous soil element at the moment of trenching

Fs=sinφ′/sinθ=Fs1+Fs2+Fs3=

(22)

其中，Fs1和Fs2同式(12)、(13)。Fs3由黏聚力产生，其表达式如下：

(23)

式中：c′为有效应力状态下的黏聚力。

(24)

4 槽壁稳定性时空效应实践验证

4.1 工程背景

西安地铁钟楼站为西安地铁二、六号线换乘车站，车站位于东大街与北大街交汇口处，沿东大街东西向敷设。车站主体全长约为247.5 m，整体形状较为异形，基坑深度为27.10～30.15 m，宽度约为27.5～40.3 m，平面示意见图10。车站主体采用半盖挖顺作法施工，支护体系由1 000 mm厚地下连续墙+四道水平支撑+立柱桩临时支撑组成。

图10 基坑及试验槽段平面示意 mFig.10 The schematic plan of the deep excavation and test trenches

4.2 监测方案

综合考虑成槽深度以及现场施工条件，以车站标准段南侧3幅较深槽段ALQ33、ALQ26和BLQ31作为研究对象进行全程监测，各试验槽段平面位置如图10。以槽段ALQ33为例，单幅槽段具体监测方案如图11所示，监测的主要内容包括：土体水平位移、地表沉降以及土压力分布。测斜管A-E和A-M分别布置在槽段端部和中部，距槽壁垂直距离均为60 mm，深度为30 m；为避开人防工程，土压力测孔S-E和S-M同样布置在离槽壁垂直距离为60 mm的端部和中部，沿槽段长度方向与测斜管位置平齐，深度方向每隔5 m埋设一个土压力盒，测孔总深度为40 m；地表沉降监测点同样在槽段端部和中部沿槽段宽度方向不等距各布置1组，编号为D-E(1～3)和D-M(1～3)，离槽壁垂直距离依次为1,3,5 m。

4.3 结果分析

1)土体侧向位移。图12所示为测孔B-E和B-M在地连墙施工各阶段引起土体侧向位移的变化情况(正值表示土体向槽内变形)，可以看出:成槽阶段土体整体向槽内方向变形并且侧向位移随深度呈不断减小的趋势，测孔B-E和B-M最大位移分别为10.79，12.46 mm，均发生在地表左右；混凝土浇筑阶段，在混凝土侧向应力补偿作用下，土体被挤压向槽外方向变形，此时测孔B-E和B-M最大位移分别为-8.81,-9.64 mm，位移最大值均发生在孔深10.50 m；混凝土硬化阶段，由于侧向浇筑压力消散，土体进一步向槽内方向变形但变化较小，此阶段土体最大侧向位移增量分别为4.26，5.21 mm。

a—B-E测孔；b—B-M测孔。— 成槽；— 混凝土浇筑；— 混凝土硬化。图12 地下连续墙施工全过程土体侧向变形Fig.12 Lateral deformation of the earth under construction of the diaphragm wall

从单幅地连墙施工全过程来看，成槽阶段土体向槽内方向变形最大，即是槽壁最危险的阶段，进一步对比成槽阶段两个测孔发现:测孔B-M土体侧向位移整体大于B-E，且主要发生在孔深10 m范围内，表明土体侧向变形在浅层出现了较为明显的空间效应。因此在成槽时，应避免开挖槽段周围堆载，特别是槽段中部区域。此外，成槽后应尽量减小施工间歇，及时吊装钢筋笼和浇筑混凝土，确保槽壁稳定。

2)地表沉降。图13所示为槽段ALQ33和ALQ26施工全过程4组地表沉降监测点的变化规律,其监测布点位置相同。从中可以看出:地表沉降随地连墙施工不断累积并逐渐趋于定值;槽段ALQ33和ALQ26施工完成后最大地表沉降分别为13.19，17.41 mm，发生位置为ALQ33段和ALQ26段的D-M1和D-M1位置测点处。从垂直槽段方向来看，地表沉降随离槽壁距离的增大而减小；从平行槽段方向来看，槽段ALQ33施工时地表沉降表现出了一定的空间效应，槽段中部地表沉降相较于端部偏大。而槽段ALQ26施工时中部和端部的地表沉降大致相等且沉降量较大，并未表现出空间效应，可能是因为槽段ALQ26周围施工荷载集中，施工机械来回行走对地表沉降产生了较大的影响。

a—ALQ33段；b—ALQ26段。— D-E1;— D-E2;— D-E3;— D-M1; — D-M2;— D-M3。图13 地下连续墙施工全过程地表沉降Fig.13 The subsidence under construction of the diaphragm wall

a—S-E1测孔;b—S-M1测孔。图14 地下连续墙施工全过程土压力分布Fig.14 Evolution of earth pressure under construction of the diaphragm wall

3)土压力分布。图14所示为测孔S-E1及S-M1在地连墙施工各阶段槽段外土压力分布情况，分析地下连续墙施工全过程地表下5，25 m深度处土压力变化发现，测孔S-E1成槽阶段5，25 m深度处土压力分别减小至初始应力的 92.31%和98.43%；混凝土浇筑阶段5，25 m深度处土压力分别增大至初始应力的123.38%和100.22%；混凝土硬化阶段5，25 m深度处土压力分别为初始应力的114.58%和99.77%。测孔S-M1土压力变化规律与S-E1相同，但相同深度处土压力变化幅度较大，成槽阶段两个深度处的土压力分别为初始应力的85.12%和101.04%；混凝土浇筑阶段分别为139.19%和102.82%；混凝土硬化阶段分别为130.58%和102.37%。一方面说明地下连续墙施工对浅层土体扰动较大，另一方面说明空间效应对土压力的分布有一定程度的影响。

5 结束语

1)地下连续墙成槽施工应尽量减小施工间歇，充分利用时效作用，在成槽完成后尽快吊装钢筋笼和浇筑混凝土，确保槽壁稳定安全。

2)增大泥浆重度可以提高槽壁稳定性，但相较于提高泥浆液面高度效果有限。提高泥浆液面高度对槽壁浅层土体稳定性影响显著，因此周围环境复杂时应根据现场实际情况充分考虑泥浆液面超高的有利作用。

3)通过理论分析和现场实测数据得出：成槽阶段槽壁中部处的浅层土体相较于端部更容易受到施工扰动，从而影响槽壁稳定;在成槽过程中应避免开挖槽段周围堆载及重车走动，可以减小槽壁中部变形以及延缓时效作用降低的速率。