三维有限元非线性导热计算程序FemHC

刘瑜， 朱可可， 万秋里， 王成恩

(1.上海交通大学 机械与动力工程学院，上海 200240； 2.中国航空发动机集团有限公司沈阳发动机研究所，沈阳 110015)

0 引 言

当在更严格和更复杂的条件下进行结构导热研究时，非线性导热问题分析变得更加重要，如涡轮叶片导热计算、功能梯度材料导热计算等。导热问题中存在各种非线性，例如，非线性热源和汇、非线性边界条件(如边界上的辐射和非线性对流换热)、具有相变的导热和与温度相关的材料特性等。为解决这些非线性问题，通常使用有限差分法、有限元法、有限体积法和边界元方法等。本文介绍一种新开发的基于有限元法求解温度相关各向同性材料热传导的程序FemHC。

1 非线性结构导热问题的有限元法

描述区域中固体导热的控制方程为

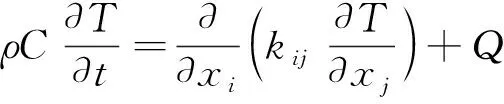
(1)

式中：为温度；为密度；为比热容；是热传导张量分量；为单位体积的内部热生成源项；下标和满足爱因斯坦求和规则。所有的变量都可能是空间坐标=(,,)和时间的函数。方程的求解需要指定合适的初边值条件，即

(2)

式中：为边界上点的坐标；为应用通量，一般给定具体的值；为对流换热通量，

=(,,)(-)

(3)

式中：为对流换热系数。

以上边界条件包含固体与环境之间的热传导和对流传热。物性系数、、和可以是温度的函数，因而各方程可以是非线性的。

方程的初始条件为

(,0)=()

(4)

初边值问题的有限元求解分为2步：(1)空间离散，将控制方程的弱形式在典型的有限单元上进行离散，得到关于温度的常微分方程，即得到温度节点值的常微分方程组；(2)采用合适的方法，如有限差分法，对第一步得到的常微分方程组进行时间离散，得到关于+1时刻节点值的代数方程组。定常问题可以不考虑时间项，根据问题的非线性特点选择合适的迭代方法求解即可。

1.1 半离散有限元模型

将对流传热区域离散为适合有限单元的集合,在方程两侧乘以权函数()，在单元上进行积分，对高阶导数项进行分部积分，在边界积分中应用边界条件，得到离散元弱形式为

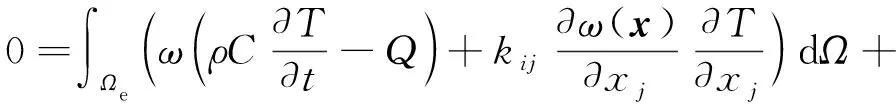
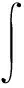
(5)

将温度的有限元近似代入到弱形式中，得到半离散的有限元模型。在选择的近似时，假设时间变化和空间变化可以分离，即

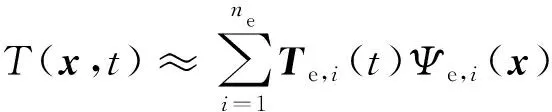
(6)

式中：为节点的温度向量；为单元的节点数目。

将其表示为矩阵形式为

(7)

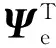
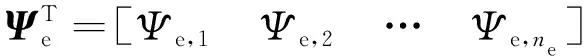
(8)

令权函数()=e,()(=1,2,…,)，并将温度的插值函数代入到弱形式中，得

(9)

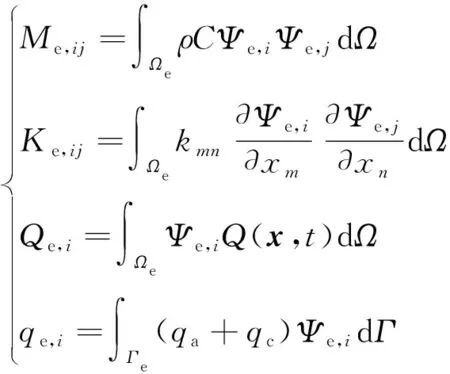
(10)

采用有限元法对控制方程和边界条件离散并进行装配，得到非线性常微分方程组

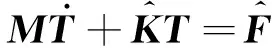
(11)

单元系数矩阵和向量可以表示为向量形式

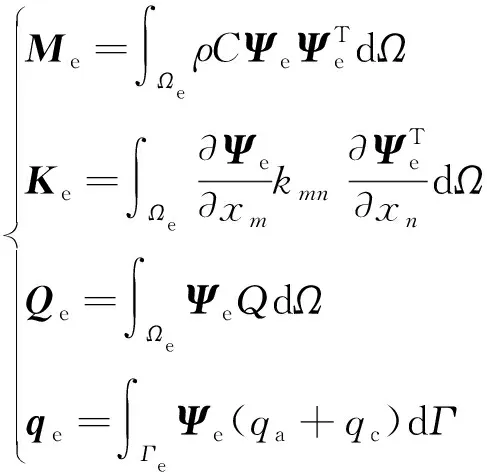
(12)

本文设计软件采用的方程形式是最一般的情形，材料物性、边界条件和体积源项都是温度的函数。装配矩阵可以表示为

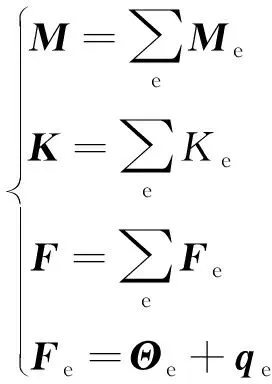
(13)

在式(13)中，求和在网格所有的单元上进行。一旦插值函数确定，单元几何就确定，可以得到全局装配方程为

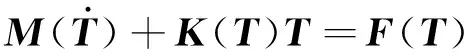
(14)

对边界面通量进行计算，最终得到

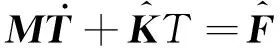
(15)

其中：

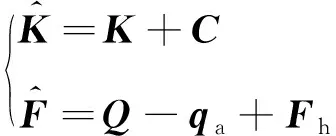
(16)

式中：为源项；为边界上指定的热流通量在边界上的积分；为对流换热边界对刚度矩阵的贡献；为对流换热边界对右端项的贡献。和的表达式为

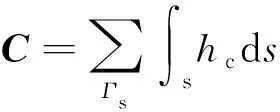
(17)

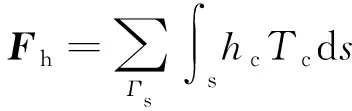
(18)

式中：为对流换热边界。

1.2 非线性方程组的求解

根据是否为时间相关问题，可将非线性方程组的求解分为2类：稳态问题和瞬态问题。稳态问题可采用Picard迭代方法求解。瞬态问题要先对时间导数项进行离散，然后对每一时间步的非线性方程组采用Picard迭代。为增加稳定性，还可以采用松弛算法，具体细节见文献[6]。在程序中，线性方程组采用BiCGStab算法，并采用开源线性方程组求解器Eigen求解。

2 有限元程序的实现

为开发有限元计算涡轮叶片结构导热的程序，首先建立有限元计算框架。该框架具有如下特点：(1)可以统一处理一维、二维和三维问题；(2)能够根据具体问题灵活指定边界条件，将网格与求解过程完全解耦；(3)不限制有限单元类型，支持添加新的有限单元；(4)支持混合单元；(5)能够方便处理多区域问题(如果计算域不同区域具有不同的物性参数)和多物理场耦合问题。

2.1 统一处理一维、二维和三维问题

当前流行的CAE软件，如FLUENT和OpenFOAM等，不具有全维度模拟能力，FLUENT只能处理二维和三维网格，OpenFOAM只能处理三维网格。OpenFOAM要计算一维和二维问题时，只能在三维网格上指定合适的边界条件模拟一维和二维问题。在程序开发和问题求解的初始阶段，往往要先从简单的一维和二维问题着手，在一维和二维问题取得满意的效果后再解决复杂的三维问题。如果算法能同时处理一维、二维和三维问题，那么可以为程序的开发和问题的求解提供很大便利。

以经典热传导方程为例，说明有限元法如何统一处理一维、二维和三维问题。其控制方程为

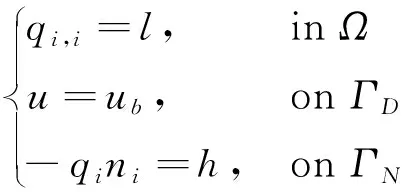
(19)

根据傅里叶定律，

=-,,=

(20)

式中：为温度；为热通量；为热传导系数。控制方程的伽辽金有限元离散公式为

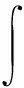
(21)

式中：为单元形状函数。

根据问题维度的不同，式(21)的积分对象不同：对于三维问题，其为体积分和边界上的面积分；对于二维问题，其为面积分和边界上的线积分;对于一维问题，其为线积分和边界上的点积分。因此，可以根据问题维度将体网格单元和组成边界的面，或者面网格单元和组成边界的线，或者线网格单元和组成边界的点都视为有限单元存储。将点统一以三维坐标存储，采用高斯积分公式对这些积分项进行近似计算。

以三维问题为例，对于体积分，有

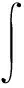
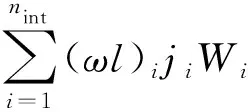
(22)

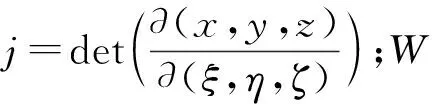
对于面积分，有

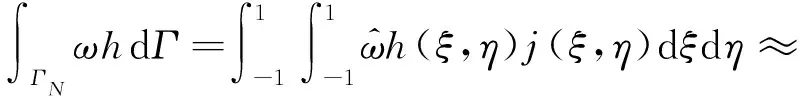
(23)

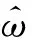
在程序中建立有限元空间时，除建立体单元的有限元，还需要建立边界上面单元的有限元；如果偏微分方程的求解算法需要考虑网格内面的面积分，还可以建立内面有限元。如此处理后，可以采用同样的方法计算体积分和面积分，因而可以统一处理一维、二维和三维网格，增加程序的灵活性和适用范围。

2.2 将网格与求解过程完全解耦

根据具体问题，灵活指定边界条件，将网格与求解过程完全解耦。数值模拟往往需要考虑多种边界条件类型，如果在网格文件中包含所求解问题的具体边界条件，当需要改变边界条件类型时，需要在网格生成软件中更改，较为繁琐。为将网格与求解过程完全解耦，本软件设计单纯网格文件和边界条件文件。

2.2.1 单纯计算网格文件

网格输入依赖于3个文件，分别是网格节点文件node.txt、网格单元文件element.txt和网格边界文件boundary.txt。将某二维计算域(1,5)×(1,1)均匀剖分为9个线性四边形单元，网格文件截图见图1～3。网格边界文件是在计算域划分网格时得到的，与具体的问题无关，因而可将网格文件与求解过程解耦。

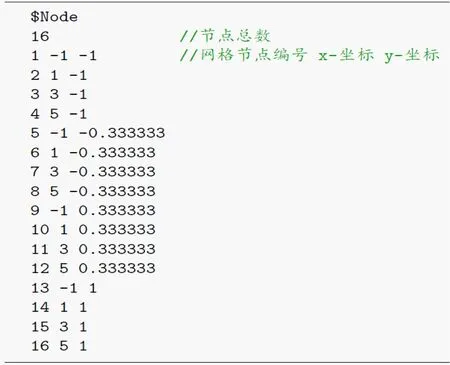
图 1 网格节点文件

图 2 网格单元文件

图 3 网格边界文件

2.2.2 边界条件文件

程序求解需要根据具体问题指定相应的边界条件，由boundaryType.txt指定，相应的文件示例截图见图4。对于具有多个变量的偏微分方程，不同的变量在同一边界上一般会有不同的边界条件。为此，每个变量都需要存储边界条件。存储的边界条件数据分为2类：(a)Dirichlet边界，存储的基本数据包含Dirichlet边界的体单元编号和该体单元在Dirichlet边界上的节点编号，可以用C++的容器map存储；(b)需要进行面积分的边界，存储的数据是边界面元对应的有限元空间的编号。

图 4 边界条件文件

这样处理的优点是可以将网格生成与方程求解分开，同时可以对不同变量灵活指定边界条件，容易增加求解变量，添加新的边界条件也容易。当然，就导热计算而言，只需指定温度边界条件即可。

2.3 程序框架的核心部分

(a)节点类Node。Node类存储网格节点的坐标。

(b)有限元空间类FESpace。为灵活添加有限元空间，有限元空间类设计为抽象基类。该类用于计算有限元形状函数及其导数，存储高斯积分点坐标和积分权重等。基类的派生类生成具体的有限元空间。

(c)单元类Element及其集合ElementSet。Element类存储单元类型、单元节点编号等。Element类还存储指向有限元空间基类的智能指针，在建立具体单元时对有限元空间进行构造。程序不限制有限单元的类型，支持混合单元，可以根据需要添加合适的单元。ElementSet是Element的集合，包含对Element进行操作的成员函数。

(d)边界类Boundary。Boundary类存储边界单元、边界单元所在的体单元的编号和边界条件类型。

(e)有限元节点上存储变量编号类FemIndex。FemIndex类建立单元节点上所存储变量的编号与单元节点编号的关系。为灵活处理多物理场耦合问题的变量存储和调用，可以对所有的变量统一进行编号，也可以对某一变量单独进行编号。

(f)方程装配类。方程装配类包括装配有限元离散得到的左端项矩阵BiLinearForm和右端项向量LinearForm。这2个类被设计为抽象基类，方程中具体的左端项矩阵和右端项向量为相应基类的派生类。稀疏矩阵以压缩行形式或压缩列形式存储。

图 5 exprtk字符串解析实例

由此可见，exprtk与常规的函数表达形式十分接近，exprtk读入这些字符串后将其解析为数学函数。核心类之间的关系见图6。

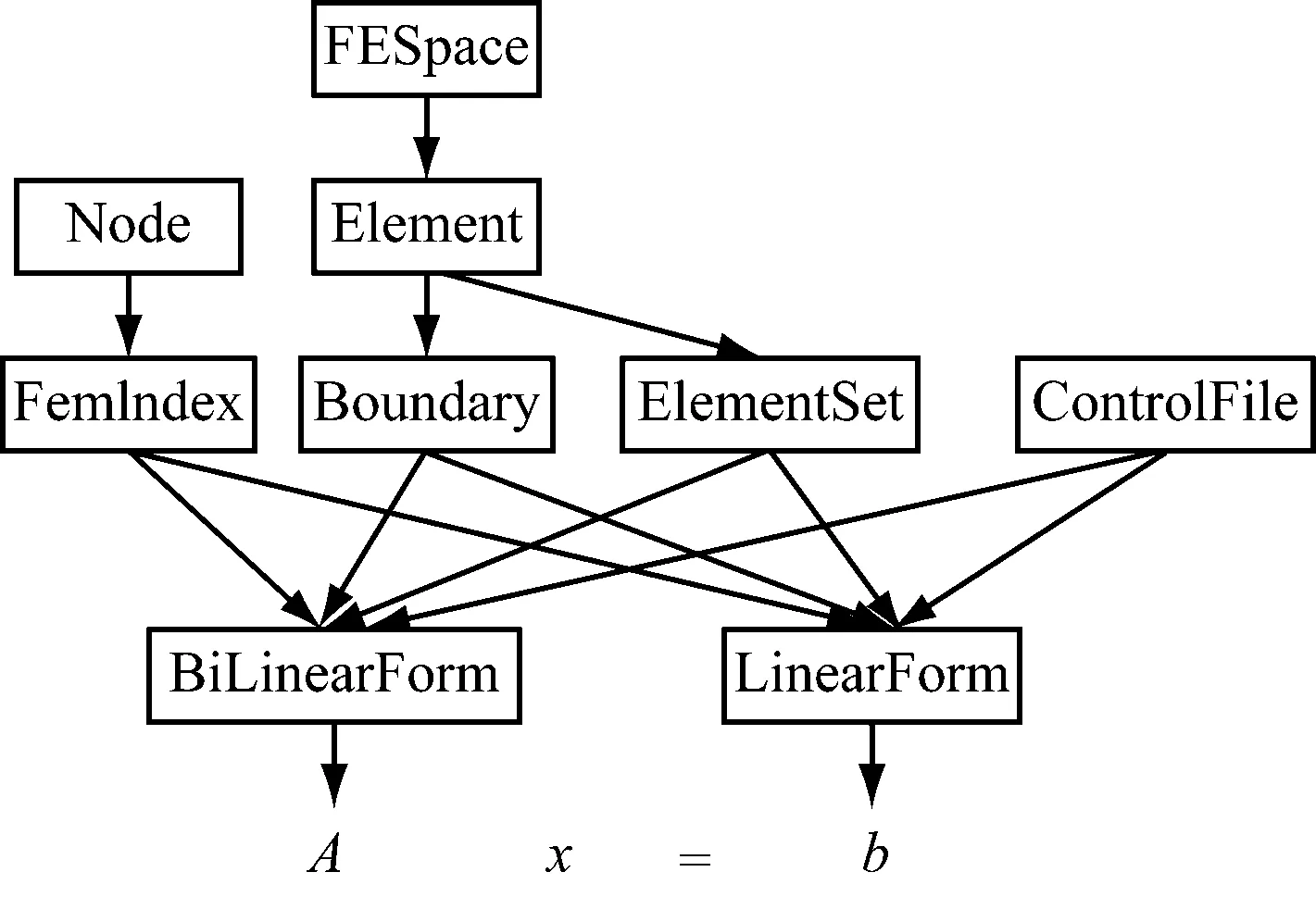
图 6 核心类之间的关系

3 程序验证和应用

为验证所采用算法及其程序实现的准确性，对若干算例进行计算，并与分析解或参考解进行比较，然后应用该程序对三维涡轮叶片的导热进行数值模拟。

3.1 二维矩形条传热问题

以长宽比为2∶1的矩形条的传热问题为例，建立传热系统的二维模型。矩形内有加热源项，左侧有热流流进，右侧温度恒定，上侧施以对流换热冷却，下侧为绝热壁面。利用格林函数可以得到该问题的定常精确解。用于测试的相关参数如下：矩形长0.10 m、宽0.05 m，材料的热传导系数为0.4 W/(m·K)，体积加热源项为=1.353×10W/m。边界条件设定为：左侧热流通量为3 500 W/m，右侧壁面给定温度25 ℃。计算时对网格进行逐次细化，采用1阶和2阶四边形单元进行计算，并估计有限元的精度阶。左下角点、上侧壁面中点和左上角点等3个测点有限元计算网格收敛性见表1，估计的精度阶见表2，可见计算结果符合有限元的理论精度。2阶四边形单元计算得到的温度场见图7。

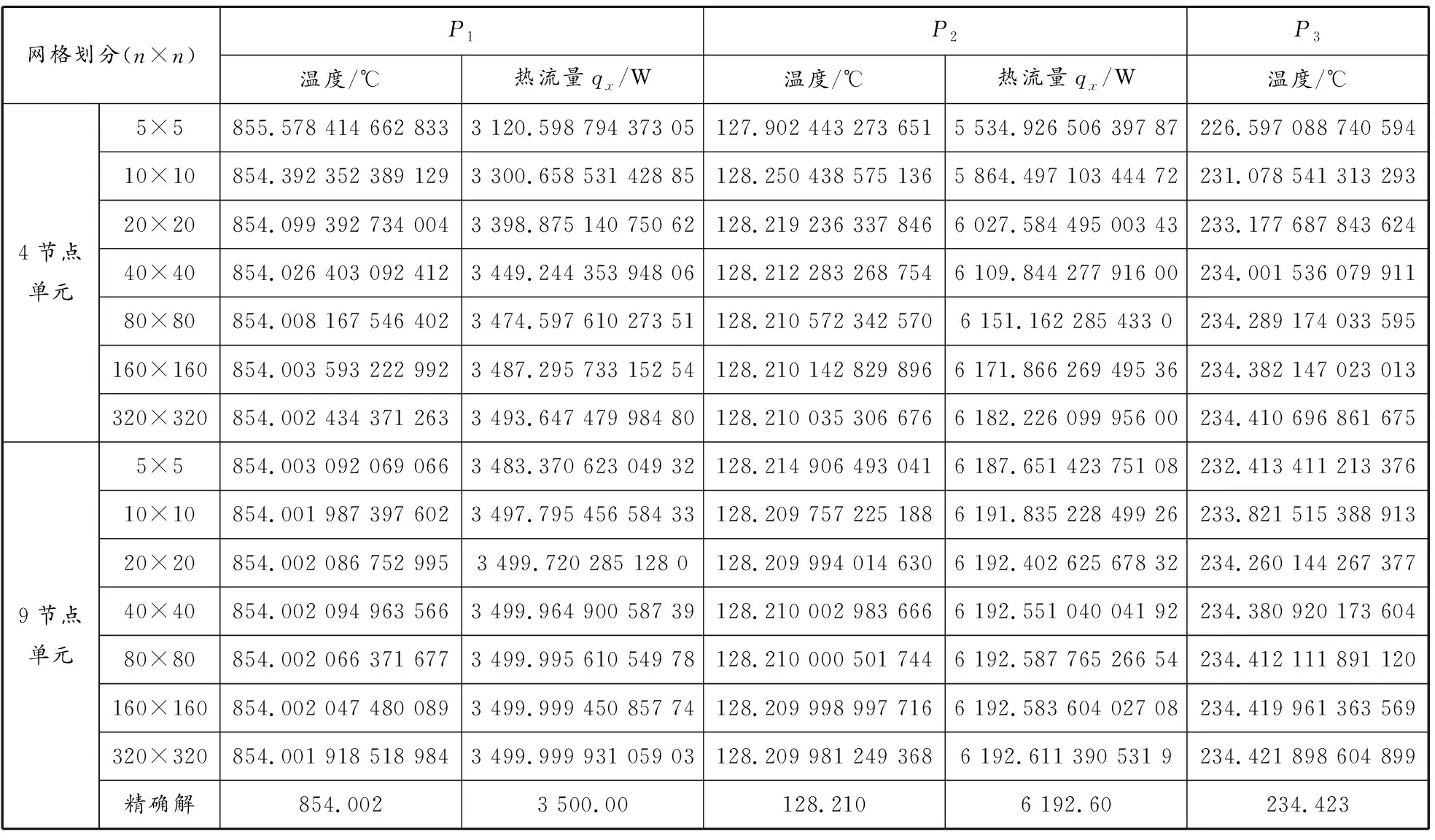
表 1 有限元计算网格收敛性计算结果

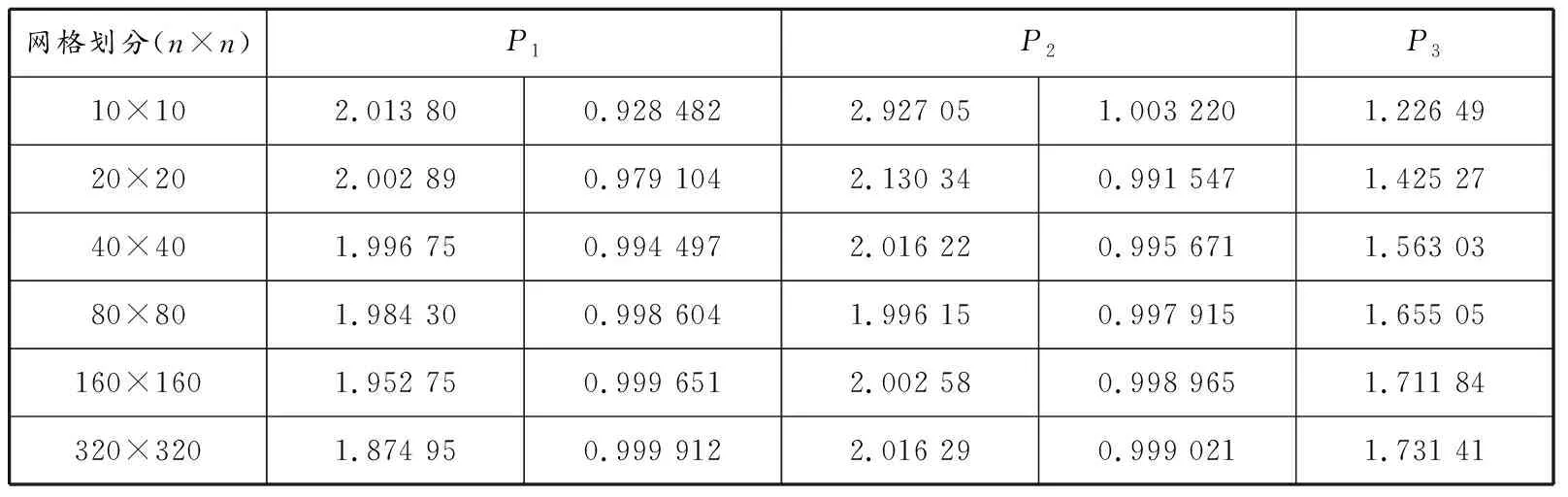
表 2 4节点单元有限元解的精度阶估计结果

图 7 2阶四边形单元计算得到的温度场，K

3.2 直条的瞬态导热

直条长度5 m，AISI 304无缝钢管。初始温度为300 K。直条左边界指定温度900 K，右侧指定Neumann条件。热扩散系数=为温度的函数()=+，其中，=2.0×10，=0.003 7。

该问题本质上是一维问题，首先采用一维网格计算。时间离散采用隐式Euler格式，时间步长取1。分别采用自由度为200的1阶单元和2阶单元计算，得到=0.4测点处的温度变化情况。采用二维网格进行计算，取直条的宽度为1，采用自由度为800的1阶和2阶四边形网格，计算测点=04、=0.5处的温度情况，并与一维结果进行对比，见图8。一维计算和二维计算都与文献[9]参考解吻合很好。

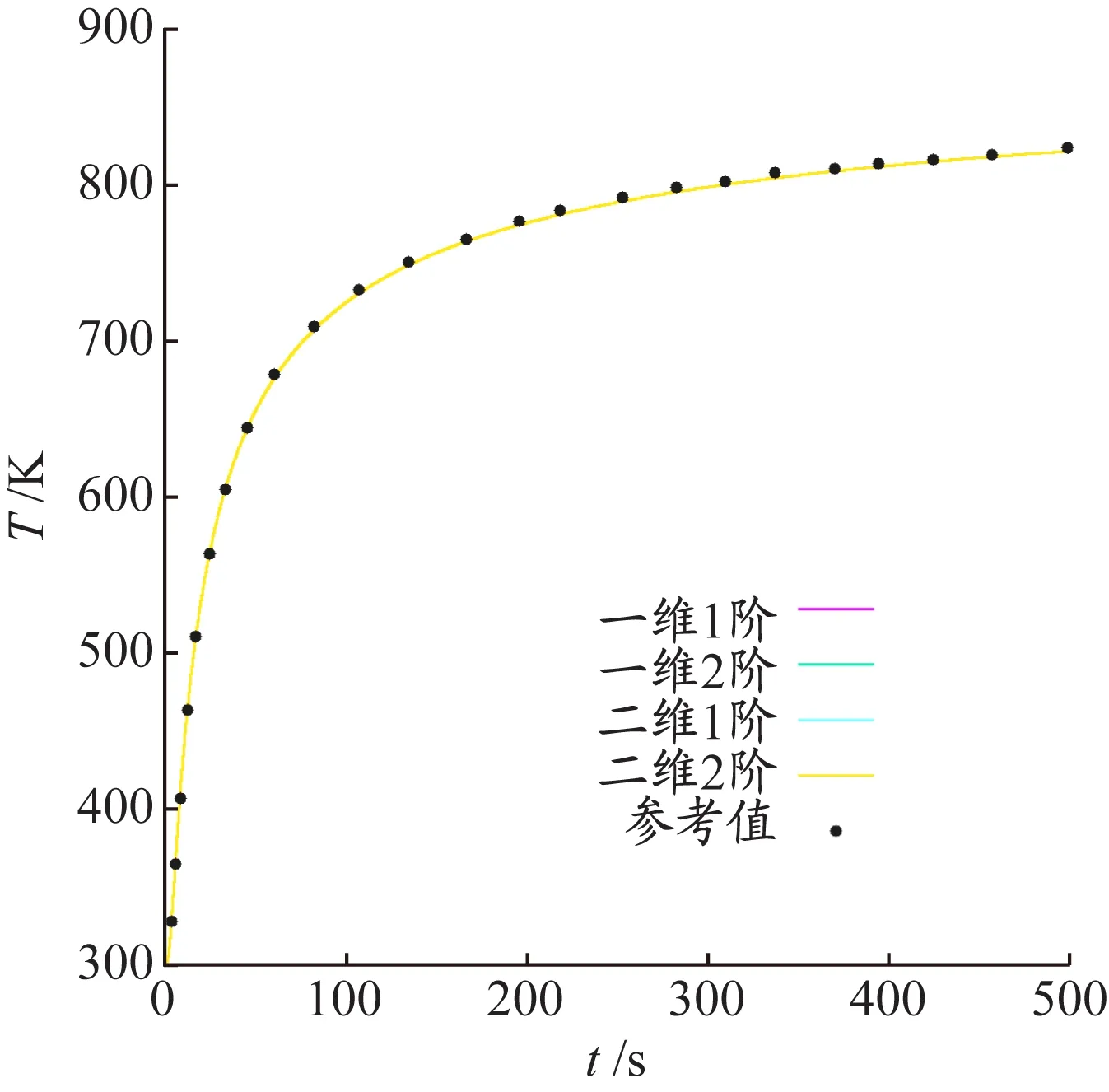
图 8 一维和二维计算测点温度变化曲线

3.3 三维功能梯度材料模拟

研究具有指数函数物性系数的功能梯度材料的导热问题，计算域为[0,]的立方体。材料的导热系数和热容系数沿方向变化，其变化方程为

(,,)=52

(24)

(,,)=2

(25)

(0,,,)=0;(1,,,)=0;

(,0,,)=0;(,1,,)=0;

(,,0,)=0;(,,1,)=0

(26)

该问题的精确解为

(27)

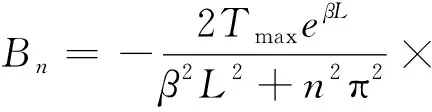
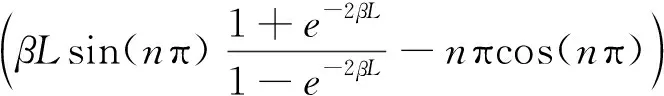
(28)

采用1阶六面体网格计算，时间离散采用隐式Euler格式，步长取0.001。不同时刻，直线(0.5,0.5,)上的温度分布曲线见图9，有限元计算结果与精确解吻合很好。

图 9 直线(0.5,0.5,z)上的温度分布曲线

3.4 具有多种材料的物体导热计算

如果导热物体的不同部分采用不同的导热材料，而且不同材料的导热系数差别很大，那么温度计算就很困难。以建筑行业的标准算例为例，该算例计算墙横截面的导热，截面的长500.0 mm、宽47.5 mm。墙体由4种不同的材料组成，最大和最小导热系数分别为230和0.029 W/(m·K)。

参照文献[10]，多种材料物体的边界条件和不同材料的导热系数见图10。上表面环境温度为0 ℃，表面热阻为0.06 m·K/W；下表面环境温度为20 ℃，表面热阻为0.11 m·K/W。表面热阻与换热系数的关系为

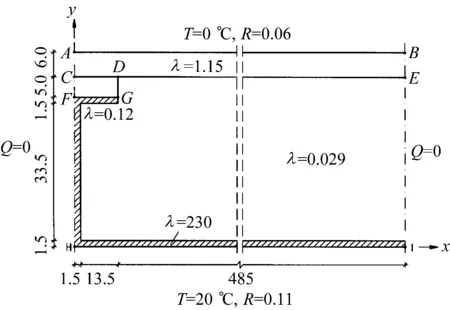
图 10 计算域和不同区域的导热系数和边界条件示意,mm

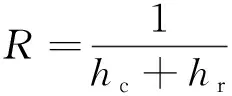
(29)

式中：为表面热阻；和分别为对流换热系数和辐射换热系数。忽略辐射的影响，近似可得物体上、下表面换热系数分别为16.667和9.090 9W/(m·K)。

计算网格包含11 636个三角形单元、4 575个四边形单元以及53 208个节点。温度场分布计算结果见图11。不同测点的温度计算结果与参考解的对比见表3。本文计算结果与参考解吻合很好，验证程序计算多区域问题的能力。

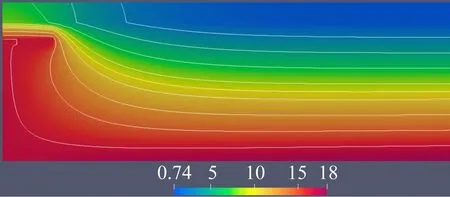
图 11 具有多种材料的物体的温度云图，℃

表 3 有限元计算的测点温度与参考解对比

3.5 不含冷却流道的三维叶片的稳态导热计算

某不含冷却流道的三维叶片及其不同面上的边界条件设定见图12，其计算网格见图13，含有67 617个四面体单元、15 802个节点。进行线性导热计算，叶片的导热系数为12 W/(m·K)。计算得到的叶片表面温度云图见图14，叶片内部切片温度云图见图15。

图 12 三维叶片导热边界条件

图 13 三维叶片导热计算网格

图 14 三维叶片温度云图，K

图 15 叶片切片上的温度云图，K

3.6 含冷却流道的三维叶片的稳态导热计算

选取某含9个冷却流道的三维叶片，计算网格见图16，具有436 952个四面体单元、90 021个节点。叶片的导热系数是关于温度的分段线性函数，作为算例测试的导热系数函数为

(30)

图 16 带冷却流道的涡轮叶片计算网格

叶片叶身以及每个冷却流道指定对流换热边界条件，换热系数和换热温度各不相同。叶身上的换热温度和换热系数分别为1 700 K和200 W/(m·K)，冷却流道1～10表面的换热温度依次为400、500、600、700、800、900、950、1 000、1 050和1 100 K，冷却流道1～10的换热系数依次为1 000、1 100、1 200、1 300、1 400、1 500、1 600、1 700、1 800和1 900 W/(m·K)，在其余边界上指定绝热边界条件。

计算得到叶片的温度云图见图17。计算在GNU/Linux系统上进行，处理器为AMD Ryzen5 3550H，其主频为2.10 GHz，当残值小于1×10时计算终止，所用时间为112 s。本例说明程序指定复杂物性参数和处理任意多个边界条件的能力。

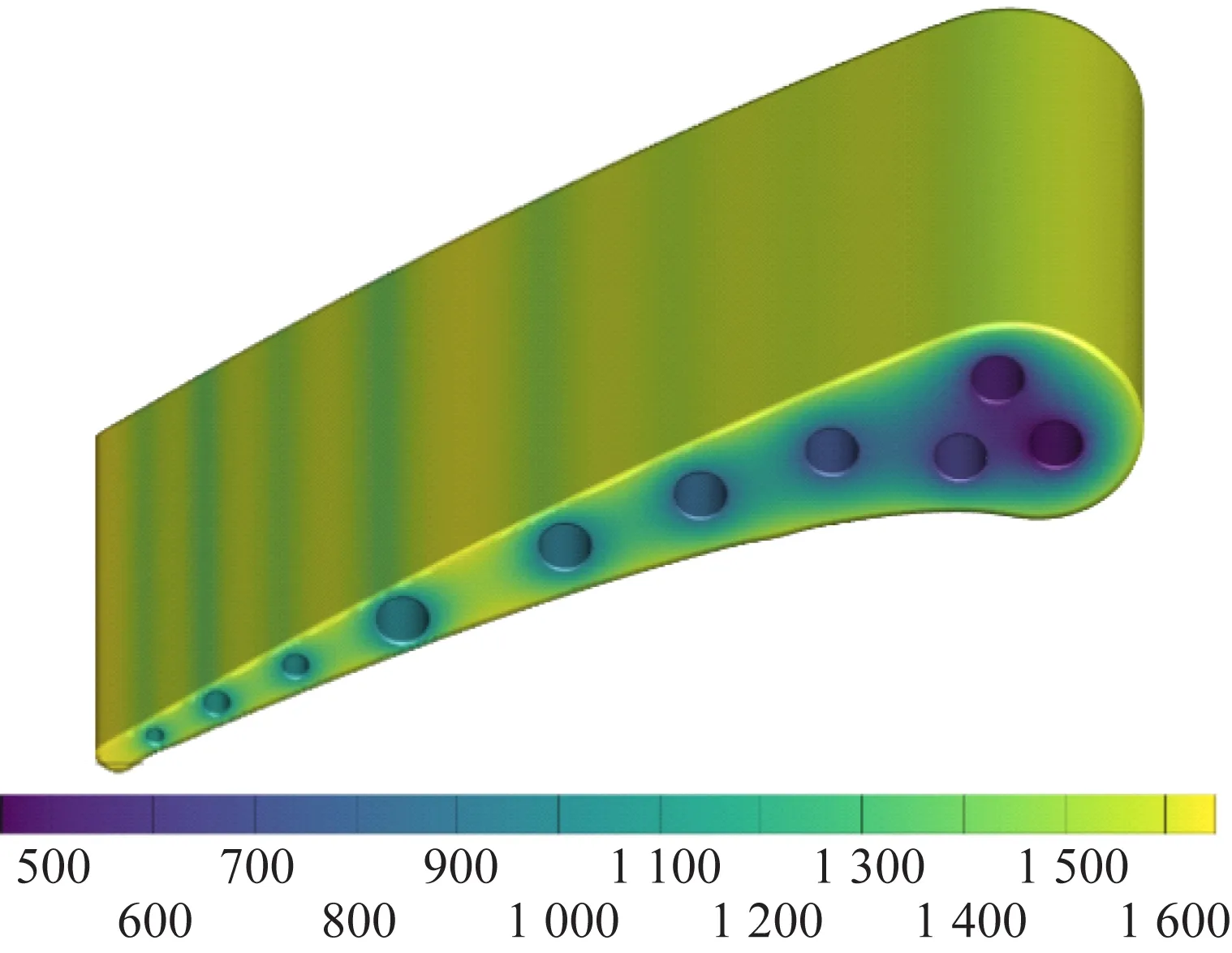
图 17 带冷却流道的涡轮叶片温度云图，K

4 结束语

介绍有限元非线性导热计算程序FemHC所采用的算法和具体的实现细节。FemHC通过将网格与具体的问题解耦，可以灵活指定边界条件，通过字符串解析库实现物性参数、初始边值条件、源项函数和计算控制参数从外部文本文件中读取，大大增加程序的灵活性。通过若干算例验证FemHC在计算线性/非线性，稳态/瞬态计算中的准确性。通过三维涡轮叶片的导热计算，表明FemHC可以用于实际涡轮叶片的计算。