基于WSNs的架空输电线路山火监控定位算法*

杨 佳， 文 斌， 许 强

(1.重庆理工大学 电气与电子工程学院，重庆 400054; 2.重庆工商大学 计算机科学与信息工程学院,重庆 400067)

0 引 言

通过实时在线监测架空输电线路走廊，在山火发生初期获取信息，对山火进行扑灭，能够有效避免山火对架空输电线路设备的危害，对减少山火损失和预防山火具有重要意义。现如今在架空输电线路走廊山火防范上使用较为广泛的措施有视频监控系统、卫星遥感、红外成像等[1～5]。以上技术均能在一定区域内监测山火并通过通用分组无线业务(general packet radio service,GPRS)公网传输。但输电线路多架设在人烟稀少地区，公网信号强度低甚至没有信号[6]。仅依赖以上一种技术进行火灾信息探测往往容易产生漏报或误报，而采用航空或者航天巡护费用高昂且巡视周期间隔长，无法应对爆发性山火[7]。因此可以在重要区域布置无线传感器网络来辅助监测火灾[8]。

林铭瀚等人[9]研制了基于无线Mesh 网络的输电线路山火预警监视系统。该系统考虑输电线路长链状结构，采用Mesh网络结构来实现WSNs辅助监控山火，并且提出了低功耗路由算法 L-MPRP，但适用于该WSNs的定位方法并未得到解决。范瑞娟、陈岩等人[10，11]都提出了输电线路故障定位算法，但其算法只适应于安装在输电线上的无线传感器网络，并不适用于输电线路走廊监控。经典定位算法主要分为两大类[12]：1)测距(range-based)定位算法，有到达时间(time of arrival,TOA)、接收信号强度指示(received signal strength indication,RSSI)等[13～15]；2)非测距(range-free)定位算法，有DV-Hop(distance vector-Hop)、质心等[16,17]。基于测距的定位算法因其搭载了其他较为昂贵的辅助定位硬件设备，一般都能达到较为理想的定位效果。而非测距定位算法没有搭载其他任何的辅助定位硬件设备，因此成本比较低，但也达不到较为理想的定位效果。输电线路走廊环境复杂，产生的噪声较大，传统RSSI算法受其影响较大，定位精确度不高，特殊的链状地理形势使得采用的无线传感器网络结构呈长链状，锚节点共线机率大，传统的三边测量法容易失效。

本文针对输电线路的特殊情况提出了一种定位算法，采用反向传播(back propagation,BP)神经网络预测未知节点到锚节点的距离，增强了定位算法对环境噪声的抗干扰能力，通过双曲线定位法来求解未知节点的坐标，解决了传统三边定位法在锚节点共线时无法定位的问题。

1 基于WSNs的输电线路山火监控模型

架空输电线路在穿越森林的区域有必要对其线路走廊以及周边区域进行实时监控，防止突发性山火引起输电线路跳闸以及烧毁输电线路设备，导致严重的经济损失。可以采用传感器网络来对山火进行监测，在终端节点安装温度、烟雾、火焰等传感器对输电线路走廊进行监测，然后通过算法判断是否有山火发生。WSNs应用在架空输电线路山火监控中时，其地理环境呈长链式，并且输电线路走廊环境复杂，引起的噪声较大，所以传统的定位算法适用性不强。架空输电线路山火监控如图1所示。

图1 架空输电线路山火监控图

为适应架空输电线路链状地理形式，山火监控时WSNs也应采用长链式网络结构。其网络结构如图2所示。

图2 网络结构

2 定位算法方法

2.1 基于BP训练的测距模型

无线电传播距离损耗对基于 RSSI 定位算法的定位精度影响很大。无线信号在环境中传播的过程中随着传播距离的增加，信号强度逐渐变弱。而最常用的传播路径损耗模型是对数正态阴影模型，其表达式如下

(1)

式中d为距离，Pr(d)为接收信号功率(距离为d)，dBm，Pt为传输功率，d0为参考距离，n为损失指数，Pl(d0)为路径损失功率(距离为d0)，Xσ均值为0，标准差为σ的高斯噪声。

在DV-Hop算法中，未知节点到锚节点的距离是校正值与最小跳数的乘积。然而在实际应用过程中，大量传感器节点是随机布撒在特定的区域内，节点间的传输方式为多跳，使用欧几里得度量来代替通信距离存在一定的误差，因此求得的平均跳距即校正值是存在误差的。只要两个节点能够相互进行通信，那么他们之间的跳数均为1跳，通过该方式求得的最小跳数同样也存在误差。最后求距离时便会造成误差累积，使得定位精度大大降低。

因此，本文采用BP神经网络来求解未知节点到锚节点的距离。采集RSSI值和最小跳数HC以及节点距离D，将RSSI值和HC作为BP神经网络的输入，距离D作为输出进行训练得到距离预测模型。

2.2 双曲线法

双曲线定位算法是一种通过将待定位节点定位在以锚节点为焦点、两锚节点之间距离为焦距的双曲线上，根据各双曲线之间的交点确定待定位节点坐标的多边定位算法。双曲线定位原理如下：

待定位节点(x,y)与锚节点i(xi,yi) 之间的距离为

(2)

将其进一步推导,有

(3)

即可到得

(4)

Zc=[x,y,K]T

(5)

(6)

根据公式可得

(7)

未知节点的坐标(x,y)可表示为

(8)

3 定位算法过程

3.1 测距模型建立过程

计算最小跳数和接收信号强度：锚节点广播数据包{ID,(x,y),HC,RSSI}。其中ID为编号，(x,y)为坐标；HC为传输路径总跳数值，初始化为0；RSSI为累计接收信号强度值，初始化为0。当节点接收到该数据包时，先根据ID号判断本地是否存有该数据包信息，若未存有则将数据包中的HC加1，RSSI值加上接收信号的RSSI值，然后将其存入本地数据并广播；若存有，则将已保存的HC数据与接收到的相应数据进行比较：接收到的值较大，则丢弃该接收到的数据包；接收到的值较小，则将该接收到的数据包HC加1，RSSI值加上接收信号的RSSI值后更新为本地数据并广播。

锚节点将最终保存的数据包发送到网络的中心节点，网络中心节点提取数据后训练距离预测模型，保存此次训练后各层之间的连接权值、阈值以及转换函数等，最后将保存的距离预测模型数据广播到全网络。

3.2 计算未知节点到锚节点距离

未知节点首先利用接收到距离预测模型数据加载距离预测模型，然后将本地数据中的最小跳数和信号强度提取出来输入到该模型中，输出便是未知节点到锚节点的距离。

3.3 计算未知节点坐标

通过双曲线定位方法求未知节点坐标。

4 分析仿真

本文用MATLAB 2016a来验证算法性能，实验仿真环境为：由于输电线路走廊呈长链状，因此本文仿真采用边长为50 m×300 m的长方形区域模拟输电线路走廊，传感器节点(300个)与锚节点均随机产生，节点通信半径都相同。在相同参数的网络环境中，取模拟实验50次的平均值作为最终结果。

本文使用归一化定位误差来评价算法，其计算方法如下

(9)

式中M为未知节点总数，R为通信半径，第i个节点的估算坐标为(xuk,i,yuk,i)，真实坐标为(xk,i,yk,i)。

在本文仿真实验中，训练样本数取决于锚节点数量，测试样本选取50个。在未说明情况下，神经网络训练参数使用表1中列出的参数，实验仿真时使用表2中列出的参数。

表1 神经网络训练参数

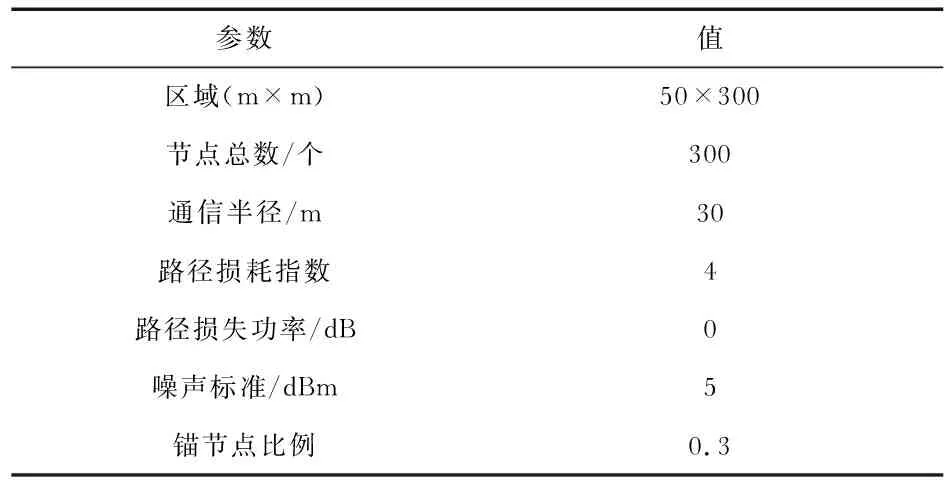
表2 仿真实验所用参数

本文将节点通信半径从10到40每增加5 m进行了仿真实验，仿真结果如图3所示。从图3中可以获知，网络连通性增强能够改善定位误差，经典DV-Hop算法应用在输电线路走廊的情形下具有较大的定位误差，本文算法和RSSI能够适应该情形。与DV-Hop算法和RSSI进行比较，节点通信半径在20 m范围内时RSSI定位效果比本文效果好，在通信半径大于20 m后，本文算法定位效果更佳。其原因是本文算法在DV-Hop算法上进行改进，继承了其定位精度受网络连通性影响的特点。

图3 不同通信半径定位误差

为了探究锚节点比例对输电线路走廊山火监控定位算法的影响，本文将锚节点比例从0.1到0.4每增加0.05进行了仿真实验，仿真结果如图4所示。从图4中可以看出，锚节点比例的增加会相应的改善定位算法效果。DV-Hop算法应用在输电线路走廊的情形下效果不理想，不能实现较为精确的定位，而RSSI算法与本文算法定位效果较为理想。本文算法与RSSI算法进行对比，本文算法在相同情况下有更好的定位效果。

图4 不同锚节点比例定位误差

架空输电线路穿越森林区域，其覆盖的线路走廊环境复杂，容易产生噪声，因此定位算法需要具有较强的抗干扰能力。本文进行实验仿真，得到如图5所示为不同噪声标准差的定位误差图。 实验仿真说明：在噪声标准差从1到10每增加1 dBm的情况下，RSSI算法定位误差随着噪声标准差的不断增加而增加，而本文算法在噪声标准差不断增加的情况下仍就能保证其定位精度。其原因是本文算法在引入BP神经网络后，其鲁棒性与容错性得到了显著的提升，使得环境噪声对本文算法的影响较小。由图5可以看出在环境噪声值较小的情况下RSSI定位算法精度高，而在环境噪声较大时本文算法定位精度高。穿越林区的架空输电线路走廊环境复杂，产生的噪声较大，因此本文算法更适合应用在输电线路走廊监测中。

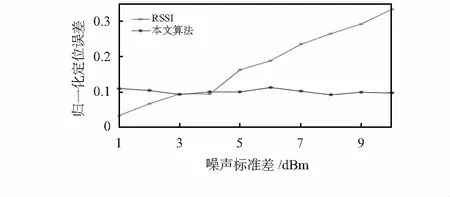
图5 不同标准噪声差定位误差

5 结束语

本文在DV-Hop与RSSI两种基本算法的基础上，考虑到架空输电线路环境复杂以及结构特殊，引入BP神经网络和双曲线法，提出了一种架空输电线路山火监控定位算法。仿真实验结果表明：本文算法能够适应架空输电线路走廊长链状结构，对其复杂的环境噪声也具有较强的抗干扰能力，在进行山火监控时能够有效定位山火发生位置。本文在锚节点比例较小时可能导致BP神经网络因样本缺失而训练失败，因此在后续的工作中主要针对锚节点数量较少时对算法进行改进。