基于多相位自定时振荡环的真随机数发生器*
陈杨兵, 吴 帆, 蒋剑飞
(1.上海交通大学 电子信息与电气工程学院,上海 200240;2.中国船舶重工集团公司第七一一研究所,上海 201100)
0 引 言
在众多高端电子设备中,随机数发生器是其处理器中的重要组成部分,可以通过它产生该系统所需要的安全密钥、进行系统服务、操作协议、绑定移动电子设备ID以及发展数字签名验证协议等。随机数的质量同样对密钥算法的安全性、操作系统的稳定性和统计模拟的准确性有着至关重要的影响,随机数的质量越高意味着其越难以被预测,系统的安全性也就越高。在生活和工作中,集成电路的应用越来越广泛,对电路的集成度、工作效率和可移植性有了更高的要求,所以对随机数发生器的研究也变得越来越重要。
随机数发生器被分为真随机数发生器以及伪随机数发生器两种主要类型。真随机数发生器的熵源一般为不确定的、随机的事件或者一些物理现象,例如热噪声,电路抖动或者原子裂变等,通过这些自然界中无法预测和控制的现象产生随机数序列,这种随机数没有确定的趋势和显著的规律性,不容易被预测和攻击,但同时也不容易控制[1,2]。
本文针对传统反相器振荡环的频率随级数线性减小、对工作环境、电压和工艺变化非常敏感,容易受到外部的攻击等不足,提出了一种基于多相位自定时振荡环的熵源结构,采用异步电路中常用的密勒单元作为随机熵源的基本单元,通过多个密勒单元有序组合实现熵源结构的振荡。
1 真随机数发生器的工作原理
自定时振荡环是由密勒单元和反相器组成的封闭环状电路,如图1所示,其中密勒单元的个数应当不少于3个。

图1 两相位的自定时振荡环结构[2]
在图1中,自定时振荡环第i级的基本单元中反相器的输入连接到密勒单元的一个输出,其中反相器的输入名为Ri,该级密勒单元的另一个输入名为Fi,对应输出名为Ci。每一级密勒单元的输入Fi连接到上一级的输出Ci-1,每一级反相器的输入Ri连接到下一级的输出Ci+1。
在自定时振荡环的振荡行为模型中,通过创建冒泡(bubble)位和标志(token)位对其进行行为描述。其中,bubble和token的概念主要来源于两阶段通信协议的描述[3],主要如下:1)如果振荡环中某级的输出Ci与其上一级的输出Ci-1不相等,则认为振荡环的该级中存在一个token位;2)如果振荡环中某级的输出Ci与其上一级的输出Ci-1相等,则认为振荡环的该级中存在一个bubble位。若把自定时振荡环中bubble位的数量记为NT,token位的数量记为NB。则在对振荡环的设置中,设置振荡环可以产生自主的振荡信号,则需要满足以下三个前提条件:1)自定时振荡环的级数不应该少于3级;2)自定时振荡环中bubble的数量应该大于等1;3)振荡环中token的数量为一个正偶数。
有关研究表明,在高频范围工作时,自定时振荡环鲁棒性会明显优于反相器组成的振荡环结构。自定时振荡环中会存在两种振荡模式:猝发振荡模式以及均匀间隔振荡模式。有关研究数据证明,在遵循自定时振荡环的设计规则前提下,可以通过配置初始化状态来设置自定时振荡环的振荡方式,而不需要考虑其他因素的影响。
如果自定时振荡环设置的初始状态中bubble和token的数量越接近,则该振荡环输出中含有抖动的时钟频率越高,并且此自定时振荡环越接近均匀振荡模式[4]。
当token与bubble的数量之比大约等于输入端Fi到输出端的静态延时Dff与输入端R到输出端的静态延时Drr之比时,振荡环就可以实现均匀振荡。在本文提出的设计中,密勒单元通过使用KCU116 FPGA中的查找表单元LUT进行实现,因此如果忽略连线之间的延时,可以近似将Dff和Drr认为是相等的,因此可配置自定时振荡环初始状态中的bubble和token的数目保持最小差,振荡环就会工作在均匀振荡模式,即满足下面的条件NT/NB=Dff/Drr,NT=NB。
两相握手协议的自定时振荡环具有上述诸多优点,但通过使用Virtuoso仿真软件仿真发现,四相握手协议的自定时振荡环与两相握手协议的自定时振荡环相比,在相同级数的条件下,其具有振荡频率更高,熵源随机性更好的特点。因此在上述自定时振荡环的结构上,本文对熵源结构进行了进一步优化,采用四相握手协议组成自定时振荡环,其中单级四相握手协议的自定时振荡环结构如图2所示。

图2 单级四相协议自定时振荡环结构
为了设置四相协议自定时振荡环的初始状态,需要在各个密勒单元上均添加置位Set和复位Reset信号,当Set置位信号为1,而Reset复位信号为0时,该密勒单元的输出则为1。当Set置位信号为0,Reset复位信号为1时,该密勒单元的输出则为0,其他情况下,密勒单元的输出则和输入相关,即当两个输入相同时,输出与输入相同,当两个输入不相等时,输出则保持上一个状态。
2 真随机数发生器的电路设计
2.1 整体结构
本文提出了一种利用多相位自定时振荡环结构为熵源,以查找表以及CARRY进位链结构为熵源提取电路的真随机数发生器结构,整体系统设计结构如图3所示。
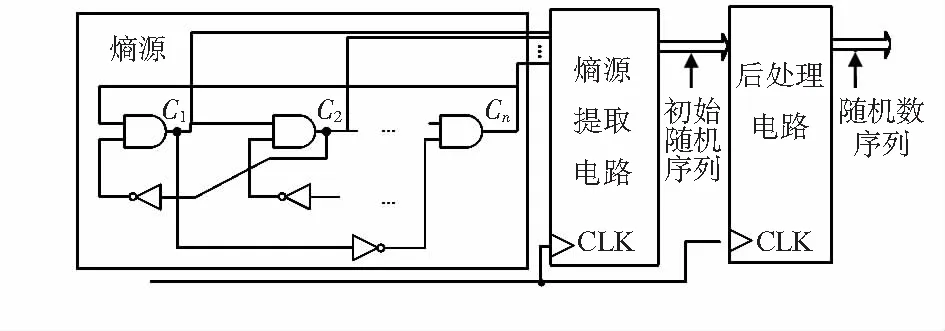
图3 真随机数发生器整体设计
主要由熵源产生电路、熵源提取电路、后处理电路三个单元电路部分组成,因为本设计是基于KCU116 FPGA平台,FPGA包含基本可编程逻辑单元(CLB),其中包括了查找表(LUT),因此本文电路中实现的多相位自定时振荡环采用6输入LUT实现。
2.2 熵源提取电路
本文新提出的熵源提取方法是基于现场可编程门阵列(FPGA)中的CARRY单元具有延迟的基本特性,通过对自定时振荡环的上升及下降边沿进行采样得到随机序列。相比于其它通过提高振荡环的频率从而提高吞吐率的方法,本方法主要是通过对单个振荡周期的上升及下降边沿进行解码提取熵源,提出本方法的前提依据是因为随机数的吞吐率与采样时钟频率成比例,在一定情况下,采样时钟的频率越高,真随机数的吞吐率就越大。
在Xilinx FPGAs中,每个CLB中均包含有2个CARRY延迟链单元,本质上其是用来实现加法、乘法和分支等功能的,通过设置其原语输入等操作,则也可以利用其对熵源进行延迟采样,一条CARRY延迟链中包含有多个延迟级,因此可以通过把各个延迟级连接到触发器中保存其采样数据,这样就可以实现从连续不断的模拟数据转换为单个的数字[5]。本结构能够被用来进行高时钟采样并且实现高吞吐量的模数转换。
CARRY延迟链的内部结构由CARRY快速延迟单元和多个连接到其输出的触发器组成,在采样时钟上升沿,延迟链的输出被D触发器捕捉到。而这些输出是反映出自定时振荡环的内部振荡状态,为了能够捕捉到全部抖动状态,可以将采样时钟频率提高到振荡时钟频率的2倍,这样可以大大提高真随机数的产生速率[6]。
本文随机数发生器中,熵源和熵源提取电路被实现为2个独立的部分。熵源系统中所有的随机性都是由信号边缘的不确定性产生的。熵源信号首先通过CARRY延迟单元进行延迟传输,再通过连接的触发器进行采样,从捕获的数据片段解码出信号边缘的位置,然后熵源提取电路产生输出一个随机比特,采样时序如图4所示,其中Ci为自定时振荡环的输出,CLK为时钟采样信号,D1…D4是D触发器的采样输出,因为Ci中包含抖动不确定性,因此D触发器采样也就带有不确定性。

图4 熵源提取电路的采样时序
2.3 后处理电路
真随机数发生器中常使用后处理电路对产生的原始随机数序列进行纠偏。常用的后处理电路方式有冯诺依曼纠偏法以及异或链方法等。冯诺依曼纠偏法经常被用来消除随机数序列存在的局部偏置,可以在很大幅度上提高输出随机数的随机性质量,并且这种方法的电路设计非常简单,容易实现。但是这种后处理方案减少了输出的随机数的位数,使得随机数发生器的输出速率降低,影响整个器件的处理速度。在正常环境下,本电路产生的随机数已经具有很好的随机性,但当环境或者其他因素变化时,产生的随机数据流可能出现偏置现象,即0和1的比例不是1︰1。为了增强电路的鲁棒性,本电路添加一个异或链进行纠偏[7]。本电路不会降低比特流输出速率。假设随机数发生器产生0的概率为p,则产生1的概率为1-p,那么经过上述后处理电路之后,产生0的概率则变为
P(X=0)=2p(1-p)=2p-2p2
(1)
其产生1的概率则相应变为
P(X=1)=1-P(X=0)=1-2p+2p2
(2)
3 系统实现与仿真分析
3.1 电路系统的实现
传统由CMOS构成的密勒单元在FPGA中无法实现,但在Slice单元中的LUT可以通过定义真值表的方式来实现需要的逻辑功能,密勒单元也可通过这种方式实现。
如图5所示,在基本的六输入LUT单元中,两个输入a,b分别为密勒单元的正向输入与反向输入端,Set置位和Reset复位信号则为初始状态控制信号。输出端为O,由于密勒单元存在的一种情况保持上一状态不变,因此需要将查找表LUT的一个输入端和输出端相连接,本次使用的四相协议的自定时振荡环结构,因此每级振荡环都需要使用2个LUT进行实现,其LUT配置的真值表均为64'hEE00FFEE8800FF88。LUT单元在FPGA电路板上资源丰富,排列整齐而且紧密,使得本结构在FPGA中很容易得到满足,通过四相协议的自定时振荡环的每一级都固定为2个LUT后,需要手动布局布线,固定每个密勒单元的位置。

图5 单级四相协议在FPGA上实现原理
3.2 系统仿真与分析
在FPGA上实现电路系统后,通过使用通用异步收发器(universal asynchronous receiver transmitter,UART)串口,把真随机数发生器产生的随机数据导入到PC端。在PC端输出至少100万位的随机数后,需要对这些随机数序列使用NIST套件软件进行测试,由于NIST的15项标准测试指标中有一部分测试标准的数据量要求最少为100万位。本文中设计的真随机数发生器采用资源占用最少的原则来进行配置,此自定时振荡环选择了最小的级数,即3级在250 MHz的采样时钟频率下对产生的随机数进行多次测试,其中每项测试取统计平均值,测试结果如表1所示。

表1 NIST测试结果
本文提出的四相协议自定时振荡环结构由1个3级自定时振荡环、3个熵源提取电路和1个后处理单元组成。因为每一级自定时振荡环使用2个LUT6,熵源提取电路使用1个LUT6和4个寄存器,XOR链使用1个LUT6。最后,后处理使用1个LUT6和4个寄存器。将本文提出的方案与其他真随机数发生器架构设计进行比较,如表2所示。对于每一个作为对比的随机数发生器,本文均分析了所提供的吞吐量和所需的硬件资源。此外,还考虑了硬件实现,包括实现平台和熵源。

表2 本设计与其他随机数发生器对比
对两相协议自定时振荡环和四相协议自定时振荡环在相同级数的情况下的振荡情况做出对比,在Virtuoso中仿真结果如图6所示,可表明,四相协议的自定时振荡环振荡频率明显高于两相协议的自定时振荡环。

图6 四相(上)和两相(下)振荡波形
理论上,示波器可以测量周期抖动和周期偏差,但由于采样频率误差的引入,不适合测量偏差很小的抖动值。因此,采用引入的理论抖动积累特性来测量累积抖动并计算初始抖动值。如图7所示,同时测量了同为3级的两相自定时振荡环和四相协议自定时振荡环结构的周期抖动。可以看出,四相协议的自定时振荡环产生的抖动更加具有随机性。

图7 抖动测量
4 结束语
本文基于四相协议的自定时振荡环结构提出了一种全数字真随机数发生器系统,在Xilinx KCU116 FPGA上进行实现,通过使用四相协议的自定时振荡环保证了系统的高频情况下的抖动频率;通过直接例化查找表保证密勒单元的实现;通过手动布局布线保证采样传输的精度。仿真结果表明:本文提出的真随机数发生器结构不仅在高频情况下具有较高的高斯抖动,而且具有高振荡频率,基于全数字电路设计,具有很好的移植性,而且具有更大的随机性。

