太阳辐射和地温对冰盖下水温的影响
杨开林,郭新蕾,王 涛,付 辉,潘佳佳
(流域水循环模拟与调控国家重点实验室,中国水利水电科学研究院,北京 100038)
1 研究背景
太阳辐射到达地表(水面、冰面和雪面)后,一部分被地表反射回到大气,一部分透射穿过地表,其它部分被地表吸收。对雪盖(snow cover)、冰盖和水体而言,太阳辐射是一种热能补充。雪盖是指冰盖表面上由各种形式的积雪组成的大范围雪面。在太阳辐射透射穿过雪盖和冰盖进入水体被吸收的过程中,冰温和水温都会增加。由于冰盖力学强度是随冰温的增加而减小的[1],所以太阳辐射的透射将使冰盖力学强度降低,特别是在开河期,随着气温升高和太阳辐射强度的增加,冰温和水温的增加必然加剧冰盖底部的融解和冲蚀,加速冰厚的热衰减[2],使得冰盖在风力和水流的作用下更易于崩溃,形成开河。因此,正确地描述太阳辐射在水、冰和雪中的反射、透射和吸收规律,是准确预报河、渠和水库等冰情发展变化的基础。
目前在水库和湖泊水温分层研究中,一般认为太阳辐射净辐射ϕsn的50%~60%在水面就被吸收,另外40%~50%穿过水面向下传播[3-4]。Perovich 等[5]的观测研究表明:在0℃以下冷雪覆盖的情况下,太阳净辐射ϕsn几乎全部被雪盖吸收;对于裸露冰盖,只有可见光能够透射穿过冰盖进入下面水体,而红外线在冰盖表面就被完全吸收。这是因为冰的盐度、密度、气泡含量和晶体结构等物理性质存在着垂直的变异性,在结构上,冰盖上表面有10 cm左右是由粒状冰组成,其中含有气泡、液体和杂质,下部主要由柱状冰组成,这导致了表面附近透射辐射大量被吸收。随着雪盖的消失,冰温逐渐上升,在冰盖解冻前,冰盖内部几乎是等温的,温度在-2 ℃到0 ℃之间。Henneman 等[6]归纳分析前人的研究,给出了可见光辐射能ϕsnvis与总辐射能ϕsn的比率cpar=ϕsnvis/ϕsn=0.443 ~0.483,与天气状况有关,晴天取较小值,阴天取较大值。Briegleb 等[7]在模拟北极气候系统模式CCSM3中,认为30%可见光区和100%近红外线区净辐射在雪盖表面很薄一层就完全被吸收;其余70%可见光区透射穿过雪盖,然后穿过冰盖到水体中,在透射和散射的过程中被逐渐吸收。Arst等[8]2000—2003年间观测了芬兰和爱沙尼亚的9 个淡水湖在可见光波段(波长0.4~0.7 μm)的冰和雪的反照率、冰和水的消光系数等重要参数。杨开林[9-11]基于现有的原型观测资料,研究了水面、冰面和雪面对太阳辐射的反射规律,提出了水冰雪反照率参数化通用模型;建立了适用于冰期计算分析的渠系与大气的热交换模型,包括太阳辐射、长波辐射、水面蒸发和对流热交换的非线性模型,提出了利用历史天气资料把热交换模型线性化的方法;在此基础上,研究了冰期明渠水温的数学模型,考虑了水面与大气的热交换及明渠衬砌结构、导热性能和地温等因素的影响。
需要指出的是,虽然在水、冰和雪对太阳辐射的反射、透射和吸收规律方面的研究已经取得明显进展,但是在河渠冰情发展模型中的应用相对滞后。例如,在现有的冰盖下河渠水温发展数学模型中,普遍采用国际著名专家沈洪道[12]的线性化热交换模型,其特点是水温的变化只受水体与冰盖交界面热交换的影响,没有考虑太阳辐射可见光透射和河渠地温的影响。由此产生的问题是:(1)不能定量确定冰下水温的大小,以及水温对冰盖热增长和热衰减的影响;(2)不能合理地回答为什么冰盖糙率系数不是随时间递减或者趋近一个定值的问题。
本文的主要目的是,首先研究太阳辐射在雪盖、冰盖和水体中的透射和吸收规律,分析冰和水消光系数的变化规律及水的消光系数的参数化;然后,建立冰下一维水温模型,研究太阳辐射和渠床地温对水温的影响,以及太阳辐射对冰盖糙率发展规律的影响。
2 太阳辐射在雪盖、冰盖和水体中的透射和吸收
如图1 所示,太阳辐射在地表(水面、冰面和雪面)的净辐射ϕsn可划分为两部分:可见光波段的净辐射ϕsnvir和近红外线波段的净辐射ϕsnnir。Briegleb 等[7]在模拟北极气候系统模式CCSM3 中,认为可见光30%ϕsnvis和近红外线100%ϕsnnir在雪盖表面很薄一层就完全被吸收,其余可见光70%ϕsnvir穿过雪盖,然后穿过冰盖、水体到床底,在透射和散射的过程中被逐渐吸收。
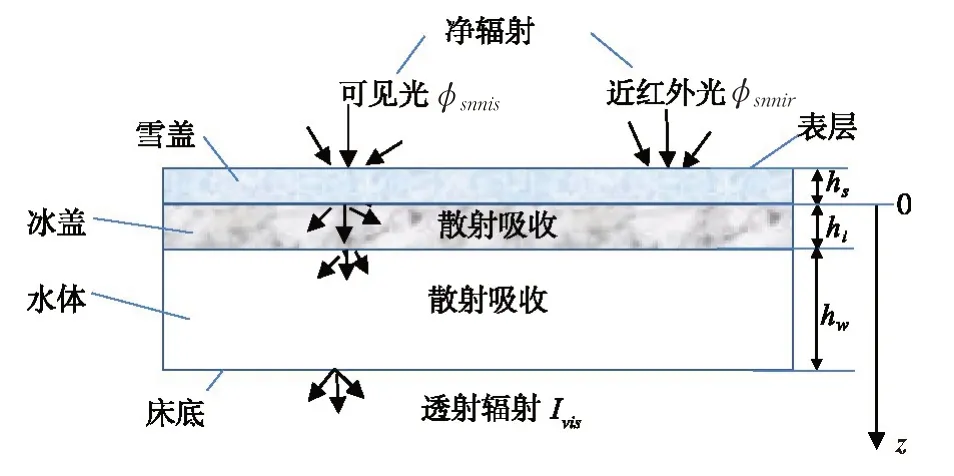
图1 太阳辐射的透射和吸收
当雪盖表面净热通量ϕsn=ϕsnvis+ϕsnnis和穿过雪盖的透射辐射为Ivis0时,则雪盖吸收的热通量是

式中Δϕsn,s为雪盖吸收的太阳辐射热通量,W/m2。根据杨开林[9]的研究,
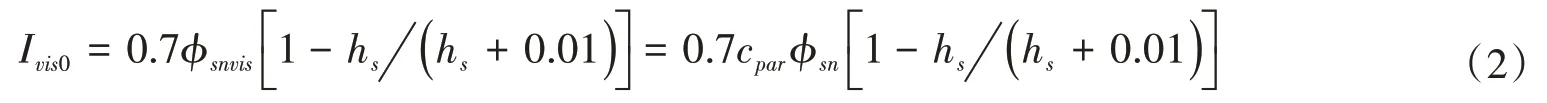
式中:hs为雪厚,m;根据Henneman 等[6]的研究,晴天cpar=0.443,多云天气cpar=0.447,阴天cpar=0.483。显然,穿过雪盖到达冰盖表面的透射辐射Ivis0随hs的增加而减小,当hs>0.1 m时,则到达冰盖表面可见光净辐射Ivis0<0.12ϕsnvis<0.06ϕsn。显然,当hs较大时,太阳辐射几乎全部被雪盖吸收。
冰和水在可见光谱范围内是透明的,根据比尔(Beer)定律(也称为Beer-Bouguer-Lambert 定律),在冰盖中可见光透射辐射Ivis按自然指数规律衰减,

式中:z为离开冰面的距离,m;hi为冰厚,m;为冰盖的消光系数(extinction coefficient)或衰减系数,m-1,是距离z的函数,与冰盖包含的气泡和杂质含量有很大关系。消光系数是指被测介质(雪,冰,水)对太阳辐射可见光的吸收大小值。消光系数大,对光的吸收能力强;消光系数小,对光的吸收能力差。
在冰盖内部点z处被冰吸收的散射辐射是

式中第一个负号“-”表示散射辐射被吸收。
穿过冰盖进入水体的太阳辐射是

式中:kvw为水的消光系数,m-1;hw为水深,m。显然,穿过冰盖的透射辐射随冰厚的增加而减小。
在水体内部点z处被水吸收的太阳散射是
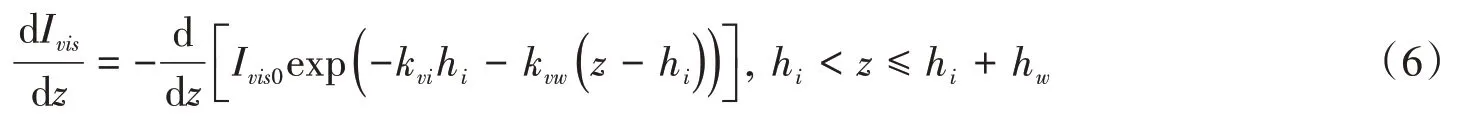
上式对于研究水库的分层水温变化具有重要意义。
当没有雪盖时,hs=0.0,这时可假设可见光30%ϕsnvis和近红外线100%ϕsnnir在冰盖表层(例如5 cm厚)就完全被吸收;其余70%ϕsnvis穿过表层向下透射和散射。在此条件下,只需令式(1)中Δϕsn,s为冰盖表层吸收的太阳辐射热通量,而Ivis0=70%ϕsnvis为穿过冰盖表层的可见光透射辐射热通量,则式(4)—(6)可描述无雪盖时太阳辐射的透射与被冰盖和水体吸收的规律。
对于敞露水面,hi=0,这时假设可见光区30%ϕsnnis和近红外线区净辐射100%ϕsnnir在水面表层就完全被吸收;其余可见光70%ϕsnvis穿过表层向下透射和散射。在此条件下,只需令式(1)中Δϕsn,s为水面表层吸收的太阳辐射热通量,而Ivis0=70%ϕsnvis为穿过水面表层的可见光透射辐射热通量,并取式(5)(6)中hi=0,则式(5)(6)可描述无冰盖时太阳辐射的透射与被水体吸收的规律。
需要说明的是,床底,例如库床、河床和渠床,一般是不透光的,所以透射通过水体的可见光将在下垫层表面被完全吸收。
3 冰和水的消光系数与冰厚和水深的参数化
Arst等[8]2000—2003年间观测了芬兰和爱沙尼亚的9个淡水湖中冰的消光系数kvi和水的消光系数kvw,其中6个淡水湖的实测结果列于表1,其中:除雪表示把雪从冰盖去除。
观测表1,冰的消光系数kvi随冰厚hi和颜色的变化而变化,显然,含有泥沙黄色冰的kvi比深灰色光滑冰的大,kvi的平均值约为1.0 m-1。

表1 实测冰和水的消光系数kvi和kvw与冰厚hi和水深hw的关系
水的消光系数kvw与水深hw有关,例如,Harku湖hw=0.3 ~1.0 m、kvw=1.60 ~2.12 m-1,Ülemiste 湖hw=0.7~1.5 m、kv=0.79~2.12 m-1,Maardu 湖hw=2.5~3.5 m、kvw=0.88 ~1.12 m-1,Ormajärvi 湖hw=3.0 m、kvw=0.56 m-1,从中可得一个重要结论:水的消光系数kvw随水深hw的增加而减小,原因是床底透光性较差,光能主要被水体吸收。换句话说,当穿过冰盖的透射辐射Ivis一定时,单位截面积不同水深的水体要吸收同样的Ivis,必然是kvw随hw的增加而减小。根据这一规律,由Harku、Ülemiste、Maardu和Ormajärvi 湖资料可以绘出图2,采用回归的方法得水体消光系数kvw与水深hw的参数化公式是
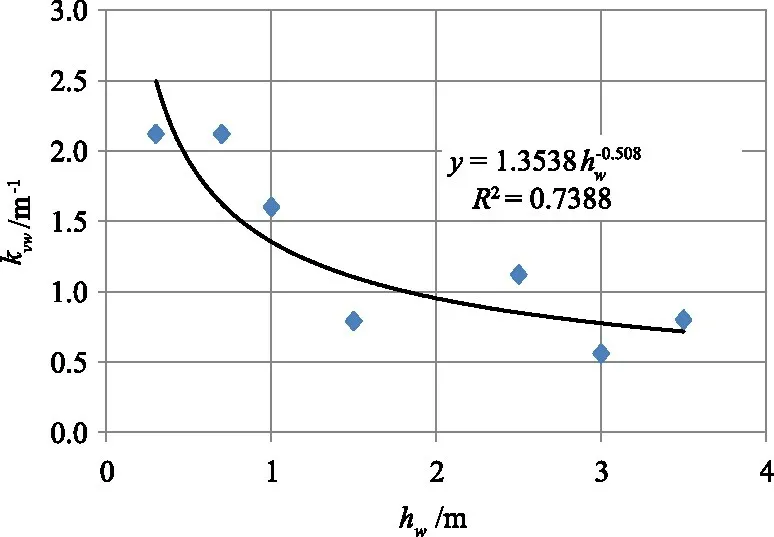
图2 水的消光系数kvw随水深hw的变化

4 冰盖下的一维水温模型
在一维条件下,冰盖下沿流向的对流-热扩散方程是
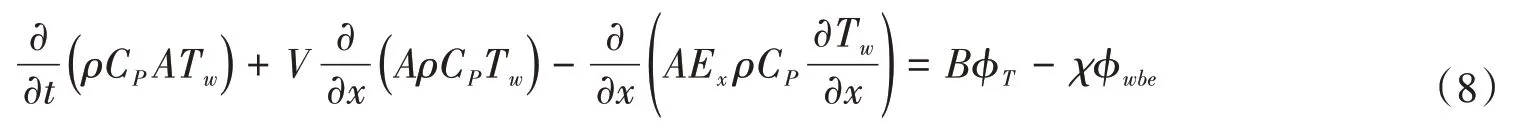
式中:左边第一项表示过水断面热量随时间的变化;第二项表示过水断面热量随水体运动的变化,又称为热量的对流传递;第三项表示过水断面热量随水体热扩散的变化;t为时间,s;x为距离,m;ρ为水的密度,kg/m3,常温下ρ=1000 kg/m3;CP为水的比热,在0 ℃时CP=4217.7 J/(kg℃);A为渠道过水断面面积,m2;Tw为水的断面平均温度,℃;V为水的断面平均流速,m/s;Ex为热扩散系数;B为水表面宽度,m;ϕT为水面(冰盖与水体的交界面)的净热通量,W/m2;ϕwbe为水与渠床(河床)热交换的等效热通量,W/m2;χ为渠道(河道)湿周,m。
在冰水力学分析中,水体热扩散项可忽略不计[12]。采用特征线方法,式(8)偏微分方程可由一对常微分方程代替,

由于冰盖隔绝了大气与水面的热交换,水面的净热通量等于冰盖和水体热交换的净热通量与太阳辐射穿过雪盖和冰盖的透射传递的净热通量之和,

式中:Ivis为太阳辐射透射传递给水面的净热通量,W/m2;ϕwi为水体与冰盖的对流热交换的净热通量,W/m2。
由式(2)(3)可得太阳辐射透射雪盖和冰盖传递给水面的净热通量

冰盖和水面热交换的净热通量可以描述为水温和冰盖底部温度的线性函数[1,12],

式中:Tm为冰点温度,一般取Tm≈0.0 ℃;hwi为水和冰盖的热交换系数,W/(m2℃)。

式中:Rw为水力半径,m。在一般情况下,冰期渠道输水流速控制在V=0.3 ~0.4 m/s,以避免发生冰塞和冰坝现象,对于宽深比较大的渠道,冰盖下输水的水力半径Rw≈0.5H,当水深H=1 ~10 m 时,hwi=619.1~448.7 W/(m2℃)。
当假设透射到水面的太阳辐射热量完全被水体吸收时,则把式(12)(13)代入式(11)并取cpar=0.45可得
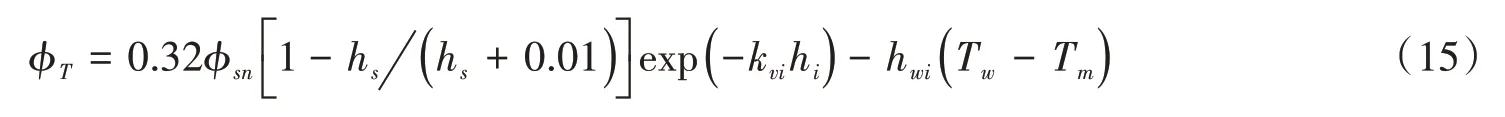
当夜间没有太阳辐射时,ϕsn=0,则
水与渠床热交换的等效热通量与水温和地温的关系可描述为[11]

式中Tbe为渠床下垫层等效地温,℃,在一般情况下,Tbe>0。对于混凝土衬砌渠道,hwbe≈1.0 W/(m2℃)。
把式(15)(16)代入式(9)得

当不考虑太阳辐射的透射和渠床地温的影响时,可得常用的冰下水温模型[12]

为分析方便,把式(17)改写为下述形式

式中

当把渠道(河道)分成为m段,在每一段参数b、c、A沿程不变,则对式(19)沿特征线积分得水温随时间变化的递推计算公式
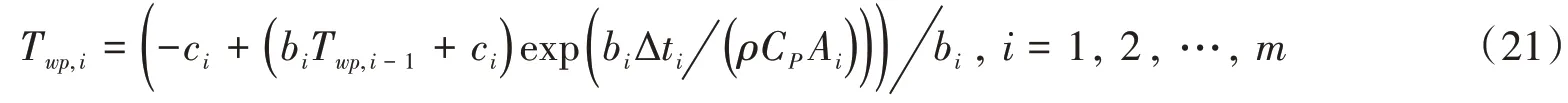
式中:下标“i”为渠段编号;m为渠段数;Twp,i-1为渠段i进口时刻ti-1的水温,℃;Twp,i为渠段i出口时刻ti的水温,℃;Δti=ti-ti-1,s。由于系数bi<0总是成立,水温Twp,i随着时间ti=t0+Δt1+Δt2+…+ Δti的增加呈指数规律变化,逐渐趋近于系数-ci/bi。由于太阳辐射ϕsn是随时间变化的,所以每个时段对应的ϕsn是不一样的。
对式(10)积分并取一阶近似可得

式中Δxi=xi-xi-1为渠段i的长度,m。
把式(22)代入式(21)消去Δti得水温的沿程分布递推计算公式

式中Qi=AiVi为渠段i的流量。上式表示水温Twp,i随着距离xi=x0+ Δx1+ Δx2+ …+ Δxi的增加呈指数规律变化。
在分析冰水动力学过程中,水力学过程和热力学过程可以分别交替独立进行,即在计算水深和流量的变化过程中,可以不考虑水温的变化,而在计算水温的变化时,在Δti时段内流速可视为已知量。另外,当需要计算相同时刻水温的沿程变化规律时,可采用特征线插值方法求解[13]。
对于均匀流,如果沿程热交换系数hwbe和地温Tbe为常数,当令Twp=0,从式(23)可得水温由渠道进口x0=0的负温度Tw0上升到0 ℃的条件,

式中xc为冰盖下水温由负转正的临界长度,m。在冰盖发展期,冰盖前缘过冷水的温度Tw0>0.1 ℃。当距离x>xc时,冰盖下将没有水内冰。
5 太阳辐射和地温对冰盖下水温的影响
由于bi<0总是成立,所以,不论冰盖前缘水温是大于还是小于0 ℃,随着下游离开冰盖前缘距离的增加,根据式(23)可得水温呈指数规律变化并趋近于一个平衡温度

对于雪盖,当气温低于0 ℃时,到达雪面上太阳辐射的70%~95%会反射回到大气;当气温高于0 ℃时,雪盖融化为雪浆,到达冰面上太阳辐射的40%左右会反射回到大气;我国纬度较小,范围在北纬3°51′—53°33′,当没有雪盖时,对于清水和黑冰,到达水面或冰面上太阳辐射的10%~33%会反射回到大气[9]。因此,当存在雪盖且气温低于0 ℃时,雪面太阳净辐射ϕsn较小;当没有雪盖时,例如开河期,冰面太阳净辐射ϕsn较大。
在现有的河渠冰水力学计算模型中,没有考虑太阳辐射和河床地温的影响,这时,由于Tm≈0.0和ci=BhwiTm≈0,所以Twc,i≈0,显然这样的结果与式(25)存在显著差异。例如,当冰盖前缘水温Twp,i<0℃,则冰盖下水温Twc,i的沿程分布呈指数规律缓慢增加,逐渐趋于Twc,i>0,而不是Twc,i=0。杨开林[2]的研究表明,由于冰盖与水体的热交换系数hwi较大,在开河期冰下水温的微小增加都会引起冰盖厚度的迅速减小。
在夜间,没有太阳辐射,ϕsn=0,所以

平衡温度Twc,i完全取决于地温Tbe的大小,并且与水体与冰盖的热交换系数hwi成反比。
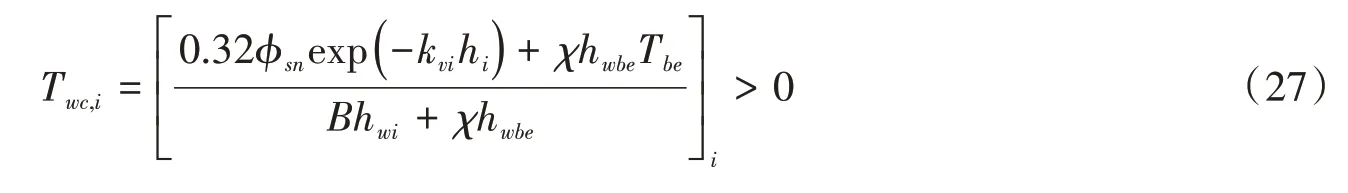
综上所述,可得重要结论:(1)冰下水温Twc,i随太阳净辐射ϕsn和地温Tbe的增加而升高,且太阳辐射对水温的影响随雪厚hs和冰厚hi的增加而下降;(2)冰下水温Twc,i与水体与冰盖的热交换系数hwi成反比;(3)冰盖下的水温白天高于夜间;(4)开河期太阳辐射ϕsn与hwi可能具有相同数量级,所以太阳辐射对冰盖下水温的影响不应忽视。
需要说明的是,太阳辐射的透射不仅影响冰盖下的水温,而且影响冰盖糙率的发展趋势。
6 太阳辐射对冰盖糙率发展趋势的影响
冰盖糙率系数是冰封河渠水力计算的基本参数,与初始冰盖发展模式和时间有关。目前对冰盖糙率系数ni的认识是:封冻开始时冰盖底部粗糙,ni值较大;封冻中期和末期时底部光滑,ni值较小。尼兹柯夫斯基总结了前苏联的大量资料,得到的冰盖糙率系数经验公式为[14]

式中:ni为初始冰盖糙率系数;ni,e为封冻期末的冰盖糙率系数,取值范围0.008~0.012;t为封冻后的天数;αn为衰减指数,αn>0。
孙肇初[15]总结了历史上黄河上游(有水内冰)及东北松花江、牡丹江和嫩江(无水内冰)实测冰盖糙率系数随时间的变化,发现冰盖的糙率系数并不随时间递减或趋于一定值,而是出现较大的波动现象。当时的分析认为这一现象是由于“不均衡输冰”而引起的,但是没有将这种现象与太阳辐射的透射和吸收联系起来。
为了解开河期冰盖糙率的变化,笔者研究团队在黑龙江漠河北极村江段开展了现场观测。黑龙江是中俄界江,那里气候寒冷,最低气温可达-50 ℃以下,封江期一般从10月中下旬到来年4月下旬开江,冰盖厚度常常超过1 m。黑龙江的冬季,不仅天气寒冷,而且降雪频繁。现场观测表明,从冰封开始一直到来年的3月末白天气温开始由负转正之前,江面长期白雪覆盖,雪厚保持在5 cm 以上,而冰厚持续热增长;一旦白天气温开始由负转正,则几小时内雪盖就迅速融化,冰盖厚度停止增长,开始形成逐日减小的趋势。从3月末直到4月中旬,气温的变化规律是:白天气温由负转正,除阴天和降雪以外,日照时间和太阳辐射强度随日期的增加而增加,中午最高气温有时超过10 ℃;但是当夜间来临,气温又由正转负,最低气温常常在-10 ℃以下。
在2017年4月6日,从冰盖上沿江横断面取出10 个冰柱,厚度在60 ~100 cm 范围内,所有冰柱底部均呈透明融化蜡烛状,其中部分冰柱底部比较平整,大部分冰柱底部凹凸不平,绝对粗糙度k相当大,最大k≈20 cm,如图3 所示。根据水力学理论,冰盖底部绝对粗糙度k值大,则糙率系数ni值也大。因此,可得一个重要结论:在冰封末期可能发生冰盖糙率系数ni变大的现象。显然,这与尼兹柯夫斯基冰封末期冰盖底部光滑糙率系数较小的结论矛盾。

图3 黑龙江漠河北极村江段冰盖底部的绝对粗糙度
为了解黑龙江冰封末期冰盖糙率不是减小而是增大的原因,下面首先分析一下黑龙江冰封末期冰情变化的特点,包括太阳辐射的反射和透射特性。
黑龙江冰封末期冰情的特点是:(1)冰盖较厚,使得白天气温开始由负转正到开江的时间长达近一个月;(2)一旦白天气温转正,雪盖几小时内就融化,可见光透射穿过冰盖的能力随着雪盖的融化而增强,不仅使得冰盖内温随时间增加,冰盖强度减小,而且使得冰下水温也升高;(3)冰盖厚度分布不均匀,可见光透射使不同冰厚垂向冰温和结构强度也产生差异;(4)不同位置冰盖类型相差较大,有黑冰和灰冰,甚至残雪等,使得不同位置冰面对太阳辐射的反照率差别较大,黑冰反照率<灰冰反照率<白冰,即黑冰面上的太阳净辐射ϕsn>灰冰的ϕsn>白冰的ϕsn;(5)夜间气温为负,白天气温转正,导致夜间冰盖热增长,而白天冰盖热衰减。
由于上述冰情特点,在白天冰盖热衰减期间,冰盖底部在冰水热交换和水流冲刷双重作用下,由于冰盖厚度、太阳净辐射和透射的不均匀分布及冰盖类型的不同,冰盖底部就会形成凹凸不平的蜡烛冰,导致冰盖底部糙率系数的增加;但是,随着黑夜的来临,冰盖进入热增长期,冰厚和强度又会逐渐增加,冰盖底部趋于光滑,冰盖糙率减小。此外,由于冰厚较大,气温开始由负转正到开江的时间较长,在一定时间内冰盖底部凹凸不平的程度可能增加,导致糙率系数ni增加且白天和夜间大小不同,即发生ni值较大的波动的现象。
7 算例
下面以南水北调中线典型渠道为例,分析太阳辐射对冰盖下平衡水温及冰盖下水温由负转正的临界长度的影响。
已知渠道断面为梯形,渠底宽b=20.0 m,边坡系数m=3.0;冬季输水流量Q=43.5 m3/s,均匀流水深H=3.0 m;水的密度ρ=1000.0 kg/m3,水的比热CP=4217.7 J/(kg℃),冰点温度Tm=0 ℃;水与渠床的等效热交换系数hwbe=0.85 W/(m2·℃),渠床下垫层等效地温Tbe=4.2 ℃。根据渠道断面形状和参数可得:冰面宽B=b+2mH=38.0 m,渠底和边坡的长度χ=b+ 2H=39.0 m,过水面积A=bH+mH2=87.0 m,水力半径=1.48 m,平均流速=0.5 m/s,水和冰盖的热交换系数=861.3 W/(m2·℃)。
2015—2016年冬季南水北调中线实测冰厚分布是,纵向分布自南向北冰盖逐步加厚,石家庄渠段冰盖厚度约10 cm(渠心),明渠末端涞涿渠段渠心最大冰盖厚度增加至28 cm;断面横向分布为渠心薄,岸边厚,岸边最大冰厚近46 cm[16]。此外,南水北调中线冬季降雪稀少,可以忽略雪对水温的影响。当取渠道进口水温Tw0=-0.01 ℃、冰盖厚度hi=0.2 m 和消光系数kvi=1.0 m-1时,应用式(24)和式(27)可分别得图4和图5所示临界长度xc和平衡水温Twc随太阳辐射净热通量ϕsn的变化关系。
当太阳辐射ϕsn=0 时,例如夜间,临界长度xc和平衡水温Twc完全取决于地温Tbe,这时,渠道水温从进口水温Tw0=-0.01 ℃增加到Twp=0 的xc=6792 m,而Twc=0.00423 ℃。从图4 可见,对于给定的已知条件,渠道水温从进口水温Tw0=-0.01 ℃增加到Twc=0的临界长度xc随太阳辐射ϕsn的增加而迅速减小,当净热通量ϕsn从0增加到450 W/m2时,xc从6792 m减小到384 m,即减小了约18倍。观察图5可得,当太阳辐射净热通量ϕsn从0 增加到450 W/m2时,冰盖下平衡水温Twc从0.00423 ℃线性增加到0.141 ℃,即增加了约33倍。

图4 临界水温xc随太阳辐射ϕsn的变化
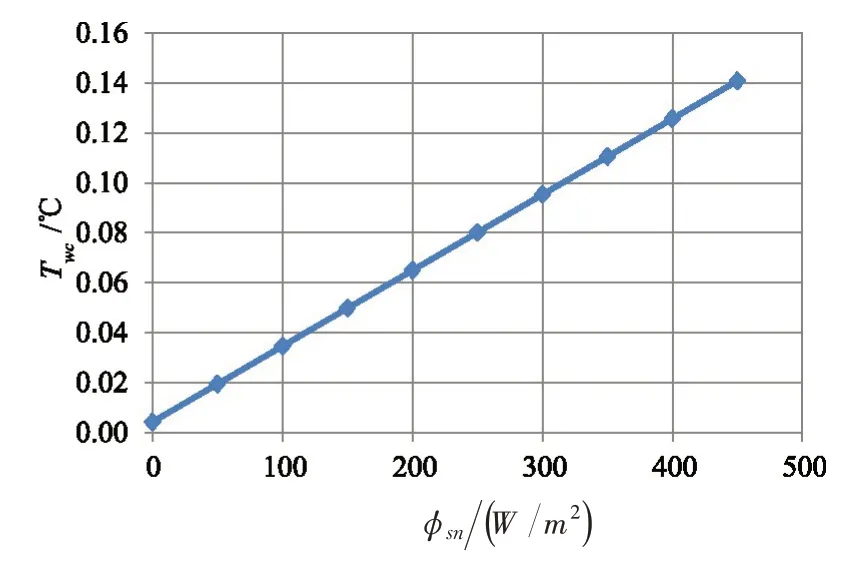
图5 平衡水温Twc随太阳辐射ϕsn的变化
综上所述,可得结论:当太阳辐射强度较大时,冰下水温主要取决于太阳辐射。
8 结论
太阳辐射的可见光可以透射穿过雪盖和冰盖进入水体,使得冰温和水温增加及冰盖力学强度降低。当雪厚较大时,太阳辐射几乎全部被雪盖吸收。可见光的透射强度在冰盖和水体中按自然指数规律衰减,冰盖消光系数kvi随冰厚和颜色的变化而变化,含有泥沙黄色冰的kvi比深灰色光滑冰的大,kvi的平均值约为1.0 m-1。水的消光系数kvw随水深hw的增加而减小,可按kvw= 1.35h-0.51w计算。
根据一维水温模型的分析,可得重要结论:冰下水温随太阳辐射和地温的增加而升高,随雪厚和冰厚的增加而下降,与水和冰的热交换系数成反比。此外,太阳辐射的透射不仅影响冰盖下的水温,而且影响冰盖糙率的发展趋势,在冰封末期可能发生冰盖糙率系数ni变大的现象。在白天冰盖热衰减期间,冰盖底部在冰水热交换和水流冲刷双重作用下会形成凹凸不平的蜡烛冰,导致冰盖底部糙率系数的增加;但是,随着黑夜的来临,冰盖进入热增长期,冰厚和强度又会逐渐增加,冰盖底部趋于光滑,冰盖糙率减小。换句话说,糙率系数ni白天和夜间大小不同,存在较大的波动现象。

