一种改进马尔科夫链的光伏出力预测方法

白雪飞

（国能黄骅港务有限责任公司，河北 沧州 061100）

随着“屋顶光伏”工程的开展，大量光伏接入配电网[1]。由于光伏电源受环境因素影响较大，光伏出力具有一定的随机性和波动性，这将对配电网的可靠性、稳定性以及配电网电能质量造成不利影响[2]。因此，建立准确的光伏出力时序模型对于光伏系统规划和运行具有重要意义[3]。

常用的光伏出力预测方法主要有支持向量机[4]、人工神经网络[5]、时间序列法[6]以及组合方法[7]等算法，文献[8]选取与预测日最接近的一组历史数据作为样本值，基于改进的灰色BP 神经网络对光伏出力进行预测。文献[9]基于贝叶斯概率原理对DFM模型进行修正，同时利用PSO优化算法建立了光伏出力组合预测模型。上述预测方法往往依赖大量历史数据来确保精度，由于分布式光伏电源具有投资小、分散广、监管力度不足等特点，光伏出力历史数据获取存在一定困难。马尔科夫链常用于预测具有随机波动性的问题，其在降水量预测、风力发电以及电力负荷预测等方面均取得显著效果。文献[10]理论推导证明了光伏出力符合马尔科夫链，并基于马尔科夫链建立了光伏出力时间序列预测模型，但原始马尔科夫链模型无法反映实际季节、天气变化等因素对光伏出力的影响。文献[11]通过对原始马尔科夫链进行数据片段细化分类进一步提高了预测模型精度。考虑天气特性、日特性以及季节特性。文献[12]基于马尔可夫蒙特卡洛模拟和谱聚类组合算法建立了光伏出力聚类与模拟模型。文献[13]提出采用加权的马尔科夫链修正残差SVM 预测模型，进一步验证了马尔科夫链模型在光伏出力预测方面的优势。

考虑原始马尔科夫链模型无法描述云层随机波动对光伏出力的影响，本文结合序贯蒙特卡洛模拟提出了改进马尔科夫链的光伏出力预测方法。

1 马尔科夫链模型

1.1 马尔科夫链基本原理

马尔科夫链是指具有无后效性的一系列离散状态序列，即下一时刻状态只与当前状态有关，而与之前的历史状态无关。不同状态之间相互转移的概率组成的矩阵称为状态转移矩阵P，如式(1)所示，其元素Pij表示由状态i转移到状态j的概率。

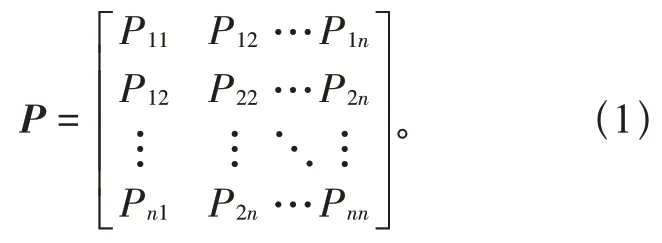
已知马尔科夫链模型的系统状态转移矩阵为P，当前t时刻系统状态概率分布为St={Pt0,Pt1,…Ptn} ，则依据式（2）可计算得到下一时刻i系统状态概率分布Si，由式（3）求得i时刻系统应处状态Si。

1.2 云层状态划分方法

状态转移矩阵是马尔科夫链模型的重要组成部分，在建立状态转移矩阵时须要对系统状态进行划分。光伏出力受辐照度直接影响，而太阳辐照强度受云层状态影响，一般认为辐照度服从Beta概率分布，但实际上如果9:00时有云层遮挡太阳光线，显然在9:01 时刻云层不可能发生明显移动。因此Beta分布函数不具备时序性，无法表征云层随时间变化对光伏出力的影响。

为研究云层状态变化过程，本文引入云层覆盖水平CCL（cloud cover level）指标对云层状态进行划分，如式（4）所示：

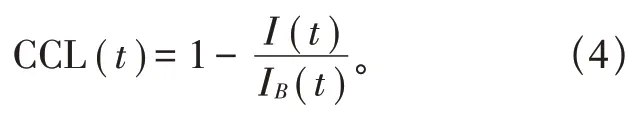
式中：CCL(t)为t时刻云层覆盖水平；I(t)为t时刻太阳辐照度；IB(t)为t时刻太阳辐照度基准值，以当天t时刻无云层遮挡时理想太阳辐照度作为基准值，该基准值在一天中随时间变化，最大值为1000 W/m2。

表1 给出了云层状态分类标准，表中依据CCL值将云层状态划分为4 类，其中CCL 值越大表示云层越多。

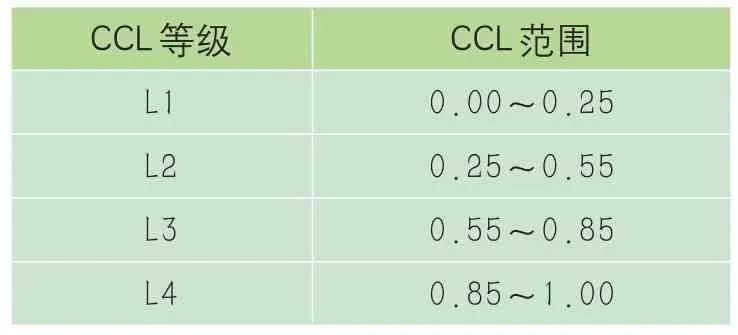
表1 云层状态分类

1.3 建立云层状态转移矩阵

原始马尔科夫链中状态转移矩阵P固定不变，在处理时序性问题时具有一定局限性。本文基于CCL指标对云层状态进行划分，利用统计学方法以15 min 为时间间隔统计计算各个时刻云层状态转移矩阵P，矩阵P中转移概率Pij由式（5）计算得到：

式中：qij(t)为t时刻云层状态由i状态转移到j状态的次数，为t时刻云层状态发生变化的总次数。

2 云层状态转移过程

光伏出力受云层覆盖水平影响具有一定随机性，通过建立云层状态转移过程可以模拟实际云层随时间变化情况。每个云层状态对应一个Beta分布，采用极大似然估计法可计算得到相应Beta 分布参数，一旦确定当前时刻云层状态，即可从其对应的Beta分布参数中抽样得到辐照度水平，进而求得光伏出力。

序贯蒙特卡洛能够灵活模拟系统中各元件所处不同状态下的持续时间，不同于蒙特卡洛模拟，序贯蒙特卡洛在模拟过程中抽样样本数为状态持续时间段数，故系统中各状态持续时间抽样方法是序贯蒙特卡洛模拟的关键。

2.1 状态持续时间抽样

状态持续时间抽样在序贯蒙特卡洛模拟中广泛应用，该方法的基本原理是采用概率抽样的方法得到系统中各状态持续时间。一般认为系统中各状态持续时间服从指数分布，式（6）为状态持续时间抽样值。

式中：T为当前状态持续时间抽样值；λ为状态转移概率；R为[0,1]区间内的随机数。

云层状态在一天内具有时序性，即不同时刻云层状态转移概率具有差异性，为此本文对公式（6）中的参数值l进行改进，基于各时刻云层状态转移矩阵调整状态持续时间，如式（7）所示。

式中：Ti为改进后云层处于状态i持续时间抽样值；Pij为当前时刻云层状态由状态i转移到状态j的概率。

2.2 云层状态转移仿真流程

前面几节基于马尔科夫过程建立了云层状态转移矩阵，以底层建模方式模拟云层随机行为。本文考虑序贯蒙特卡洛模拟处理时序问题的优势，采用改进状态持续时间抽样法将马尔科夫过程与序贯蒙特卡洛模拟结合起来，建立了具有时序性的云层状态转移过程，具体步骤：

输入历史辐照度数据；

基于云层覆盖水平CCL建立云层状态转移矩阵；

确定系统状态初始值，并依据式（7）确定当前初始状态持续时间；

依据式（2）和式（3）确定下一状态；

依据式（7）确定下一状态持续时间；

判断前后两状态是否一致。若一致，则与当前状态合并，并修改当前状态持续时间，反之得到新的状态及状态持续时间；

判断模拟时间是否超过24 h，若超过则得到一天24 h 内云层状态变化序列，反之重复步骤4 到步骤6直至达到24 h结束。

3 算例分析

3.1 仿真分析

以某一地区太阳辐照度历史数据作为样本数据，基于云层状态转移矩阵并结合状态持续时间抽样模拟得到一天24 h内云层状态转移情况，如图1所示，考虑到夜晚时刻辐照度始终为零，故设定初始状态为L4。由图可以看出，此次模拟得到的云层状态具有一定的波动性，且每个状态持续的时间呈现出较为明显的随机性，符合一天内云层实际随机变化情况。

图1 云层状态转移曲线

利用极大似然估计法计算得到不同云层覆盖等级对应的Beta 分布参数值，如表2 所示。依据模拟得到的各时刻云层状态，采用随机抽样的方法从对应的Beta 分布函数中抽取辐照度样本值。如图2 所示为一天内太阳辐照度模拟曲线，由图可以看出，由于云层状态集中处于L2 和L3 状态，云层遮挡导致太阳辐照度水平整体较低，同时随时间具有波动性。

表2 不同云层覆盖等级Beta分布参数值

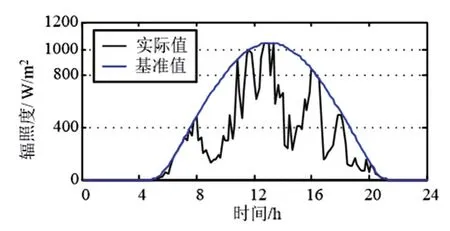
图2 辐照度模拟曲线

已有研究表明，光伏出力与太阳辐照度呈线性关系，此外光伏制造业相关数据表明，当太阳辐照度为1000 W/m2时光伏出力达到峰值。本文依据Beta分布得到的太阳辐照度抽样值可能大于1000 W/m2，因此光伏出力可由下式确定。

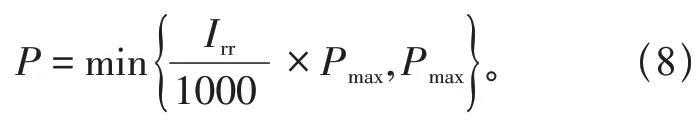
式中：P为模拟达到的光伏出力值；Irr为太阳辐照度抽样值；Pmax为光伏功率峰值。

以容量为8 kW光伏电源为例，基于太阳辐照度模拟曲线依据式（8）计算光伏出力，得到光伏出力时序曲线，如图3所示。由图可以看出，在12:00-14:00期间，模拟得到的太阳辐照度超过1000 W/m2，此时光伏出力处于峰值状态，同时，与原始马尔科夫链的预测方法相比，本文所提预测方法更加接近光伏出力实际值。

图3 光伏输出功率曲线

3.2 模型比较与误差评估

为评估所提预测方法的有效性，本文采用平均绝对百分误差（MAPE）和均方根误差（RMSE）两个指标作为评估依据。

式中：Pi为光伏出力实际值；为光伏出力预测值；n为预测样本值总数。

表3 光伏出力预测方法误差指标

本文引入状态持续时间抽样法，考虑了云层状态随机不确定性对光伏出力的影响，使得预测模型的MAPE 和RMSE 指标均有所降低，与原始马尔科夫链的光伏出力预测方法相比，本文所提方法提高了预测精度。

4 结束语

本文基于状态持续时间抽样对马尔科夫链进行改进，建立了具有时序性的光伏出力预测模型。

受地理因素限制，不同地区太阳辐照度水平具有较大差异，与借助光伏电源历史数据生成当前所需光伏电源出力曲线的直接方法不同，本文利用间接方法弥补了部分地区因缺乏光伏出力历史数据而无法预测当地光伏出力的不足。

利用平均绝对百分误差（MAPE）和均方根误差（RMSE）作为评价指标对预测模型进行评估，通过与原始马尔科夫链模型进行比较表明本文所提方法具有较高的预测精度，具备一定的可行性和实用性。