融合生活现象,叩问数学本质
——对《圆的认识》的教学思考与实践
□许现新
《圆的认识》是人教版教材六年级上册的教学内容,属于一节数学概念课,作为“圆”这个单元的起始课,它起着至关重要的作用。那么《圆的认识》该怎样教学,才能使学生易于理解和掌握呢?笔者认为,圆的认识教学应从融合生活现象中叩问圆的数学本质。
一、课前思考
在学习圆之前,学生已经学习了长方形、正方形、平行四边形、梯形、三角形等平面图形,圆这一平面图形与学生以往所学习的这些平面图形有很大的区别,圆是曲线图形。《圆的认识》是学生学习圆周长、面积、圆环、扇形等知识的基础。因而,作为“圆”单元的第一课时,在学习《圆的认识》前无特别能借鉴的前知和经验,但在学习后,它却是很多知识学习的基础。
(一)圆的数学本质是什么?
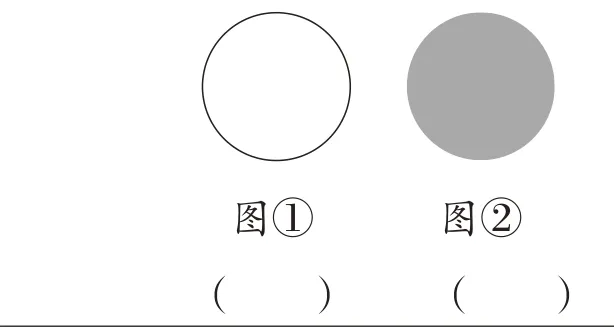
什么是圆呢?在学生的认知里,圆是平面内的那条封闭曲线(如图1),还是那个围成的圆面?(如图2)

图1

图2
我们知道,早在战国时期,《墨子》中就已经为圆写下了一个定义:“圆,一中同长也。”意思就是说“圆这种图形,有一个中心,从这个中心到圆上各点都一样长”,这说明圆的本质就是与一个定点的距离等于定长的点的集合,显然圆就是平面内的那条封闭曲线。
(二)圆的生活现象何其多?
古希腊数学家毕达哥拉斯曾说“一切平面图形中最美的是圆”。圆是几何图形中很普通又很美的图形,在我们的日常生活中普遍有圆的存在,如硬币、瓶盖、钟面、圆桌、光盘、井盖、轮胎、草原上的蒙古包、操场上的圆,有些游戏活动必须是围成圆形的圈,等等。难道圆的存在只是因为美吗?显然圆的存在既体现了圆的美,又有其广泛的实用价值,而圆的美与实用价值都来源于它的数学本质。
(三)学生对圆认识知多少?
学生在从小到大的成长过程中,经常会看到圆、用到圆、想到圆。在数学学习中从低年级起就已经接触圆了。虽然圆的出现一般用在不同图形的直观分类,或是看图列式作为直观符号形式,或是学生在解决问题的过程中作为图式分析的直观模型(如维恩图)帮助理解问题,但是在正式学习圆的知识之前,学生对圆的认识,只是在生活中、学习中比较粗浅的表面化的认知,对圆的本质概念并未触及。
于是我们做了一个课前调查。调查内容如下:
同学们,你们知道“圆”吗?
“圆”是平面内的那条封闭曲线?(图①)
“圆”是那个围成的圆面?(图②)
“圆”既是平面内的那条封闭曲线,又是那个围成的圆面?
你认为“圆”到底是什么?请你在你所认为的图下面的( )内打“√”。
经过汇总整理,我们发现被调查的一百余名学生中,有52%的学生认为圆既是平面内的那条封闭曲线,又是那个围成的圆面;有36%的学生认为圆是那个围成的圆面;只有12%的学生认为圆是平面内的那条封闭曲线。可见,学生在未学习《圆的认识》一课前,对圆的本质的认识是模糊的,绝大多数学生对圆的认识的前概念与圆的本质存在很大的偏差。
二、融合“生活现象”的教学设计
通过厘清圆的数学本质,分析圆的生活现象,调查了学生对圆的认识的前概念。在教学设计时,力求将圆的“生活现象”与圆的“数学本质”加以融合,从学生的认知发展水平和已有的经验出发,理解圆的数学本质。
(一)以生活情境导入,激发探究数学本质的欲望
在教师准确把握数学概念本质内涵的基础上,创设贴近学生生活的情境,激活学生已有认知经验,激发学生探究数学本质的欲望。
【片段1】从“寻宝物”游戏导入新课
出示“寻宝物”游戏情境:小明参加了一个寻宝游戏,宝物距离小明左脚3米,宝物可能在哪里?
(二)从生活现象中探究,架起建构数学本质的桥梁
把学生置于知识发现的真实“场景”当中,从生活现象中探究,架起建构数学本质的桥梁,更易于学生根据生活经验探究知识。
【片段2】从“宝物位置”感知“圆”的本质
师:请同学们拿出练习纸,我们用纸上面的小黑点表示小明左脚的位置,用图上距离1厘米表示实际距离1米,请你在纸上表示出你的想法。
【片段3】从“转绳子”体验“圆”的本质
师:老师这里有一根绳子,绳上有一个挂件,请你想象一下,当老师让这个挂件快速旋转起来,这个挂件留下的运动轨迹是什么样子的?
【片段4】从“操场上画圆”感悟“圆”的本质
师:圆在我们生活中很常见,篮球场上、操场上的大圆见过吗?体育老师要在操场上画一个大圆,怎样才能把它画出来?想象一下。
【片段5】从“圆规为什么能画圆”内化“圆”的本质
教师出示圆规,介绍圆规画图的方法。
师:为什么圆规能画出圆呢?请同学们利用圆规,在纸上空白地方画一个半径为2厘米的圆。
师:再画一个直径是6厘米的圆。
(三)在生活问题中应用,创设深化数学本质的机会
数学从生活中来,又回到生活中去,架起数学与生活的桥梁,感受数学就在身边,生活离不开数学。通过生活现象中数学知识的应用,给学生提供深化数学知识本质的机会。
【片段6】从“车轮为什么是圆的”深化“圆”的本质
师:在我们生活中有很多物品都是利用了圆的特性来设计的,你想到了吗?
师:为什么车轮是圆形的呢?
师:当路是平的时,为什么圆形滚动起来比较平稳呢?
师:请你想象一下,用圆、正方形、正三角形做轮,让这样的轮子转起来。圆的圆心和正方形、正三角形的中心点是如何变化的?
【片段7】从“宝物位置”升华“圆”的本质
师:老师还有最后一个问题,小明在你们说的圆上找了一圈,发现宝物并没有在这个圆上,是怎么回事呢?
三、叩问“数学本质”的教学策略
在教学设计中融合了圆的“生活现象”,那么如何利用这些“生活现象”去叩问圆的“数学本质”呢?我们尝试提出以下教学策略。
(一)想象与交流相穿插,体验数学本质
在学生探究生活现象中的数学本质时,给予学生想象与交流的机会,让学生在想象与交流中展现其个性思考,从而初步体验圆的数学本质。
通过“宝物距离小明左脚3米”这一游戏条件,让学生根据生活经验和知识去思考、去画一画。展示学生作品(如图3)。
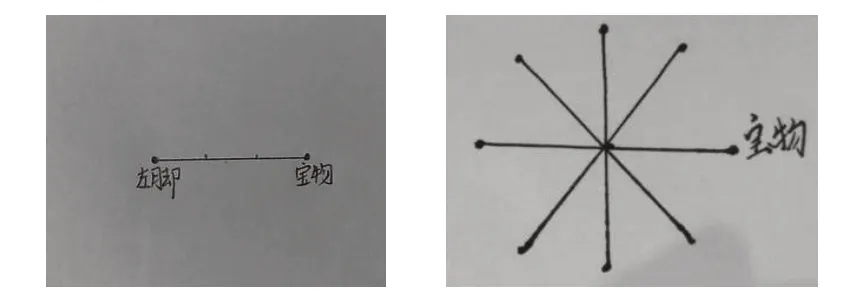
图3
教师启发引导:“这些点都距离小明左脚3米,那么像这样的宝物的位置,你还能找到吗?想象一下,如果不断地找下去,宝物所在的位置到底在哪里?”
给予学生充分想象的时间后,教师又提问:“你觉得是什么?”多名学生交流后都认为是“圆”。这时,教师借助课件向学生展示,学生发现与自己的想象是一样的,能找到无数个点,组成了圆(如图4)。

图4
在学生发现是由无数个点组成了圆之后,教师不能让学生的认识停留在这一肤浅的层面上。教师继续追问:“那么,你们说的这个圆是什么呢?”有的学生说:“它是由无数个点组成的一条线。”有的学生说:“是一条曲线。”学生的回答仅停留在圆比较直观的形上,并未回答到本质上。这时教师进一步深入提问:“这条曲线有什么特点?”学生通过小组内的讨论以及班级内的交流,最终发现:线上的每一个点到中心点的距离都是一样的,所以才形成了这样一条封闭曲线。
(二)想象与观察相融合,感知数学本质
在对生活现象的探究中,将想象与观察相结合,动中有静,静中有动,虚实相融,动静结合,形象感知圆的数学本质。
在“转绳子”中感知“圆”的本质环节中,教师提出问题:“老师这里有根绳子,绳上有一个挂件,请你想象一下,当老师让这个挂件快速旋转起来,这个挂件留下的运动轨迹是什么样的?”
给予学生想象的时间后,教师加以演示旋转,学生想象和观察后得出“挂件运动的轨迹是个圆”(如图5)。

图5
教师追问:“为什么挂件旋转留下的轨迹是个圆呢?”
学生在讨论中得出:“挂件到手指的距离是一样的,转动就会形成圆。”
(三)想象与思辨相结合,感悟数学本质
在想象中思考,在思考中思辨,使学生逐步清晰理解圆的数学本质。
在“操场上画圆”这个教学环节中,教师提出问题:“体育老师要在操场上画一个大圆,怎样才能把它画出来?”
学生有的说:“做个大圆模型。”有的说:“做个大圆规。”有的说:“人站在中间,旋转着用一支长长的笔来画。”有的说:“找一根绳子,一端固定在操场上,在另一端系一支粉笔,人拉紧绳子绕着固定点画一圈。”
在学生充分想象后,让他们各抒己见,并让学生进行思辨,最后明确,这么大的圆,要想画好,主要还是要借助“圆上的点到中心的距离是一样的”这个概念,然后根据实际情况选择合适的方法。
又如,在“圆规为什么能画圆”这个环节中,教师出示圆规,提问:“为什么圆规能画出圆呢?想象一下圆规是怎样画圆的?”学生根据想象与思辨得出:圆规两脚间距离不变,相当于圆上的点到圆心距离不变。
(四)操作与对比相渗透,内化数学本质
数学知识的建构,需要学生的多种感官参与,动手操作能让学生手脑并用,多种感官协同参与,促进知识内化,理解数学本质。
如在“圆规为什么能画圆”这个环节中,让学生用圆规画一画圆。
教师提出要求:“请同学们利用圆规,在纸上空白地方画一个半径为2厘米的圆。”
学生画好后,展示作品,在展示的过程中让学生明白只有“圆心到圆上的点的距离都相等”,才能画出完整、美观的圆(如图6)。

图6
教师又提出要求:“画一个直径是6 厘米的圆。”学生在动手实践中发现,画直径6 厘米的圆,实质上就是圆规两脚间距离取3厘米,也就是圆心和圆上点之间的距离是3厘米(如图7)。
动手操作是学生数学学习中常用的一种方法,在比较中画圆,使学生认识圆的基本结构,并清晰地理解圆的各部分之间的关系,比如同圆或等圆中半径是直径的一半,有无数条半径、无数条直径、半径决定圆的大小等等。学生在层层的探究活动中,实现了对概念本质由表及里、由浅入深逐步内化的过程。同时画圆的操作活动也是对数学本质理解后的外显过程。
(五)解释与拓展夯应用,深化数学本质
应用数学知识解释、拓展生活现象。这一应用过程,既是对数学概念本质深层次的理解,形成对知识的活学活用,又加强了数学与生活的联系。
如在“车轮为什么是圆的”这一教学环节中,教师提问:“为什么车轮是圆形的呢?”学生认为圆形平稳。
教师追问:“为什么圆形滚动起来比较平稳呢?”学生四人小组讨论后交流。
教师启发思考:“请你想象一下,圆的圆心和正方形、三角形的中心点是如何变化的?”(如图8)
学生想象后通过观察课件,演示圆形、正方形、正三角形车轮中心点与着地点之间距离的运动变化,得出:轮胎为圆形时,它的圆心到地面的距离都是一样的,就是半径,所以行驶起来比较平稳。
对源自于生活中“车轮为什么用圆形”现实问题的探讨,呈现车轮实物图,联系生活实际,引发学生的思考,让学生结合课堂探究成果,在想象与思辨中逐步体会与领悟,朴实揭密“车轮做成圆形”的原理,探寻其本质,在理解与解释中进一步深化对圆概念本质的理解。
又如在“宝物位置”的拓展应用环节中,教师抛出问题:“小明在你们说的圆上找了一圈,发现宝物并没有在这个圆上,这是怎么回事呢?”
这个问题一下子又激起了学生的思索,通过前面学习的积累,学生在想象与思辨中脑洞大开:宝物可能在地下,也可能在地上。
学生在层层的问题引领和想象、思辨下,发现宝物可能在一个球面上,教师顺势用课件展现(如图9),强化学生的想象与思辨认知。

图9
如此,通过对“宝物位置”的其他可能性判断,想象与思辨相结合,升华对“圆”的概念本质的认知,拓展学生思维。
在《圆的认识》教学中,我们淡化了对“圆”概念字面的记忆,抓住“圆”概念的数学本质,激活学生的生活经验,在融合“生活现象”中叩问圆的“数学本质”,将想象、交流、观察、思辨、操作、应用等贯穿于“圆”概念的学习过程中,凸显“圆”的数学本质,帮助学生深度建构“圆”概念,发展数学核心素养。

